【组合数学】容斥鸽巢原理
目录
- 1. 容斥原理
- 容斥原理三种形式
- 2. 容斥原理应用
- 有限重复数的多重集合的 r 组合数
- 错排问题
- 3. 鸽巢原理
- 4. Ramsey 定理
1. 容斥原理
容斥原理提供了一种通过计算每个单独集合的大小,然后修正重复计数的方法,从而得到多个集合并集大小的计算方法。它通过减去每个交集的元素个数,再加上每两个集合的交集,再减去每三个集合的交集,以此类推,来避免多重计数。
定理 1.1:容斥原理 ∣ ⋃ i = 1 n A i ∣ = ∑ k = 1 n ( − 1 ) k − 1 ( ∑ 1 ≤ i 1 < i 2 < … < i k ≤ n ∣ A i 1 ∩ A i 2 ∩ … ∩ A i k ∣ ) \left| \bigcup_{i=1}^{n} A_i \right| = \sum_{k=1}^{n} (-1)^{k-1} \left( \sum_{\substack{1 \leq i_1 < i_2 < \ldots < i_k \leq n}} \left| A_{i_1} \cap A_{i_2} \cap \ldots \cap A_{i_k} \right| \right) i=1⋃nAi =k=1∑n(−1)k−1(1≤i1<i2<…<ik≤n∑∣Ai1∩Ai2∩…∩Aik∣)其中 ∣ ⋃ i = 1 n A i ∣ \left| \bigcup_{i=1}^{n} A_i \right| ∣⋃i=1nAi∣ 表示所有集合的并集中元素的总个数。右侧的求和符号涉及不同交集大小的情况,通过交替加减不同交集的元素个数来计算最终的并集大小。
容斥原理三种形式
定理 1.2: S 是一有限集合,P1, P2,…, Pm 是同集合 S 有关的 m 个性质,设 A i A_i Ai是 S 中具有性质 Pi 的元素构成的集合(1 ≤ i ≤ m), A i ‾ \overline{A_i} Ai 是 S 中不具有性质 Pi 的元素构成的集合(1 ≤ i ≤ m),则 S 中不具有性质 Pi 的元素的个数为 ∣ A 1 ‾ ∩ A 2 ‾ ∩ . . . ∩ A m ‾ ∣ = ∣ S ∣ − ∑ i = 1 m ∣ A i ∣ + ∑ { 1 , 2 , . . m } 的 2 组合 ∣ A i ∩ A j ∣ − ∑ { 1 , 2 , . . m } 的 3 组合 ∣ A i ∩ A j ∩ A k ∣ + . . . + ( − 1 ) m ∣ A 1 ∩ A 2 ∩ . . . ∩ A m ∣ |\overline{A_1}\cap\overline{A_2}\cap...\cap\overline{A_m}|=|S|-\sum_{i=1}^m|A_i|+\sum_{\{1,2,..m\}的2组合} |A_i\cap A_j|-\\\sum_{\{1,2,..m\}的3组合} |A_i\cap A_j \cap A_k|+...+(-1)^m|A_1\cap A_2 \cap...\cap A_m| ∣A1∩A2∩...∩Am∣=∣S∣−i=1∑m∣Ai∣+{1,2,..m}的2组合∑∣Ai∩Aj∣−{1,2,..m}的3组合∑∣Ai∩Aj∩Ak∣+...+(−1)m∣A1∩A2∩...∩Am∣
习题1、求不超过 120 的素数的个数
解: 因 1 1 2 11^2 112 = 121,故不超过 120 的合数必然是 2,3,5,7 的倍数,而且不超过 120 的合数的因子不可能超过 11 。设 A i A_i Ai 为不超过 120 的数 i 的倍数的集合(i = 2, 3, 5, 7)则
∣ A 2 ∣ = ⌊ 120 / 2 ⌋ = 60 , ∣ A 3 ∣ = ⌊ 120 / 3 ⌋ = 40 , ∣ A 5 ∣ = ⌊ 120 / 5 ⌋ = 24 , ∣ A 7 ∣ = ⌊ 120 / 7 ⌋ = 17 , ∣ A 2 ∩ A 3 ∣ = ⌊ 120 / 6 ⌋ = 20 , ∣ A 2 ∩ A 5 ∣ = ⌊ 120 / 10 ⌋ = 12 , ∣ A 2 ∩ A 7 ∣ = ⌊ 120 / 14 ⌋ = 8 , ∣ A 3 ∩ A 5 ∣ = ⌊ 120 / 15 ⌋ = 8 , ∣ A 3 ∩ A 7 ∣ = ⌊ 120 / 21 ⌋ = 5 , ∣ A 5 ∩ A 7 ∣ = ⌊ 120 / 35 ⌋ = 3 , ∣ A 2 ∩ A 3 ∩ A 5 ∣ = ⌊ 120 / 30 ⌋ = 4 , ∣ A 2 ∩ A 3 ∩ A 7 ∣ = ⌊ 120 / 42 ⌋ = 2 , ∣ A 2 ∩ A 5 ∩ A 7 ∣ = ⌊ 120 / 70 ⌋ = 1 , ∣ A 3 ∩ A 5 ∩ A 7 ∣ = ⌊ 120 / 105 ⌋ = 1 , ∣ A 2 ∩ A 3 ∩ A 5 ∩ A 7 ∣ = ⌊ 120 / 210 ⌋ = 0 , |A2| = \left \lfloor 120/2\right \rfloor = 60, |A3| = \left \lfloor 120/3\right \rfloor=40, \\|A5| = \left \lfloor 120/5\right \rfloor= 24, |A7| = \left \lfloor 120/7\right \rfloor= 17, \\|A2\cap A3| = \left \lfloor 120/6\right \rfloor= 20,|A2\cap A5| = \left \lfloor 120/10\right \rfloor= 12, \\|A2\cap A7| = \left \lfloor 120/14\right \rfloor= 8,|A3\cap A5| = \left \lfloor 120/15 \right \rfloor= 8, \\| A3\cap A7| = \left \lfloor 120/21 \right \rfloor= 5, | A5\cap A7| = \left \lfloor 120/35 \right \rfloor= 3, \\| A2\cap A3\cap A5| = \left \lfloor 120/30 \right \rfloor = 4, | A2\cap A3\cap A7| = \left \lfloor 120/42 \right \rfloor = 2, \\| A2\cap A5\cap A7| = \left \lfloor 120/70 \right \rfloor= 1,| A3\cap A5\cap A7| =\left \lfloor 120/105\right \rfloor= 1, \\ |A2\cap A3\cap A5\cap A7| = \left \lfloor 120/210 \right \rfloor= 0, ∣A2∣=⌊120/2⌋=60,∣A3∣=⌊120/3⌋=40,∣A5∣=⌊120/5⌋=24,∣A7∣=⌊120/7⌋=17,∣A2∩A3∣=⌊120/6⌋=20,∣A2∩A5∣=⌊120/10⌋=12,∣A2∩A7∣=⌊120/14⌋=8,∣A3∩A5∣=⌊120/15⌋=8,∣A3∩A7∣=⌊120/21⌋=5,∣A5∩A7∣=⌊120/35⌋=3,∣A2∩A3∩A5∣=⌊120/30⌋=4,∣A2∩A3∩A7∣=⌊120/42⌋=2,∣A2∩A5∩A7∣=⌊120/70⌋=1,∣A3∩A5∩A7∣=⌊120/105⌋=1,∣A2∩A3∩A5∩A7∣=⌊120/210⌋=0,
故 ∣ A 2 ‾ ∩ A 3 ‾ ∩ A 5 ‾ ∩ A 7 ‾ ∣ = 120 – ( ∣ A 2 ∣ + ∣ A 3 ∣ + ∣ A 5 ∣ + ∣ A 7 ∣ ) + ( ∣ A 2 ∩ A 3 ∣ + ∣ A 2 ∩ A 5 ∣ + ∣ A 2 ∩ A 7 ∣ + ∣ A 3 ∩ A 5 ∣ + ∣ A 3 ∩ A 7 ∣ + ∣ A 5 ∩ A 7 ∣ ) – ( ∣ A 2 ∩ A 3 ∩ A 5 ∣ + ∣ A 2 ∩ A 3 ∩ A 7 ∣ + ∣ A 2 ∩ A 5 ∩ A 7 ∣ + ∣ A 3 ∩ A 5 ∩ A 7 ∣ ) + ∣ A 2 ∩ A 3 ∩ A 5 ∩ A 7 ∣ = 27 |\overline{A_2}\cap \overline{A_3} \cap \overline{A_5} \cap\overline{A_7} |=120 \\– (|A2| + |A3| +|A5| + |A7|) \\+ (|A2\cap A3| + |A2\cap A5| + |A2\cap A7| + | A3\cap A5| + | A3\cap A7| + | A5\cap A7|) \\– (| A2\cap A3\cap A5| + | A2\cap A3\cap A7| +| A2\cap A5\cap A7| + | A3\cap A5\cap A7|) \\+ |A2\cap A3\cap A5\cap A7| = 27 ∣A2∩A3∩A5∩A7∣=120–(∣A2∣+∣A3∣+∣A5∣+∣A7∣)+(∣A2∩A3∣+∣A2∩A5∣+∣A2∩A7∣+∣A3∩A5∣+∣A3∩A7∣+∣A5∩A7∣)–(∣A2∩A3∩A5∣+∣A2∩A3∩A7∣+∣A2∩A5∩A7∣+∣A3∩A5∩A7∣)+∣A2∩A3∩A5∩A7∣=27
定理 1.3: S 是一有限集合,P1, P2,…, Pm 是同集合 S 有关的 m 个性质,设 A i A_i Ai是 S 中具有性质 Pi 的元素构成的集合(1 ≤ i ≤ m),则 S 中至少具有一个性质 Pi 的元素的个数为 ∣ A 1 ∪ A 2 ∪ . . . ∪ A m ∣ = ∑ i = 1 m ∣ A i ∣ − ∑ { 1 , 2 , . . m } 的 2 组合 ∣ A i ∩ A j ∣ + ∑ { 1 , 2 , . . m } 的 3 组合 ∣ A i ∩ A j ∩ A k ∣ + . . . + ( − 1 ) m − 1 ∣ A 1 ∩ A 2 ∩ . . . ∩ A m ∣ |A_1\cup A_2\cup...\cup A_m|=\sum_{i=1}^m|A_i|-\sum_{\{1,2,..m\}的2组合} |A_i\cap A_j|+\\\sum_{\{1,2,..m\}的3组合} |A_i\cap A_j \cap A_k|+...+(-1)^{m-1}|A_1\cap A_2 \cap...\cap A_m| ∣A1∪A2∪...∪Am∣=i=1∑m∣Ai∣−{1,2,..m}的2组合∑∣Ai∩Aj∣+{1,2,..m}的3组合∑∣Ai∩Aj∩Ak∣+...+(−1)m−1∣A1∩A2∩...∩Am∣
定理 1.4: 设集合 S 中具有性质集合 P = {P1, P2,…, Pm} 中恰好 r 个性质的元素的个数为 N(r)则 N ( r ) = w ( r ) − ( r + 1 r ) w ( r + 1 ) + ( r + 2 r ) w ( r + 2 ) − . + ( − 1 ) m − r ( m r ) w ( m ) N(r)=w(r)-\binom{r+1}{r}w(r+1)+\binom{r+2}{r}w(r+2)-.+(-1)^{m-r}\binom{m}{r}w(m) N(r)=w(r)−(rr+1)w(r+1)+(rr+2)w(r+2)−.+(−1)m−r(rm)w(m)其中 w ( 0 ) = ∣ S ∣ , w ( r ) = ∑ 1 ≤ i 1 < . . . < i r ≤ m N ( P i 1 , P i 2 , . . . , P i r ) w(0)=|S|,w(r)=\sum_{1\le i_1<...<i_r\le m}N(P_{i_1},P_{i_2},...,P_{i_r}) w(0)=∣S∣,w(r)=∑1≤i1<...<ir≤mN(Pi1,Pi2,...,Pir)
2. 容斥原理应用
有限重复数的多重集合的 r 组合数
习题2、 S={3⋅a,4⋅b,5⋅c}的 10 组合数
解: 令 S ∞ = { ∞ ⋅ a , ∞ ⋅ b , ∞ ⋅ c } S_\infty=\{\infty \cdot a,\infty \cdot b,\infty \cdot c\} S∞={∞⋅a,∞⋅b,∞⋅c},则 S 的 10 组合数为 ( 10 + 3 − 1 10 ) = ( 12 2 ) = 66 \binom{10+3-1}{10}=\binom{12}{2}=66 (1010+3−1)=(212)=66
设集合 A 是 S ∞ S_\infty S∞的 10 组合全体,则|A| = 66,现在要求在 10 组合中的 a 的个数小于等于 3,b 的个数小于等于 4,c 的个数小于等于 5 的组合数。
定义性质集合 P = {P1, P2, P3},其中,
- P1:10 组合中 a 的个数大于等于 4;
- P2:10 组合中 b 的个数大于等于 5;
- P3:10 组合中 c 的个数大于等于 6.
将满足性质 Pi 的 10 组合全体记为 Ai (1 ≤ i ≤ 3).那么,A1 中的元素可以看作是由 S ∞ S_\infty S∞的 10 – 4 = 6 组合再拼上 4 个 a 构成的,所以 ∣ A 1 ∣ = ( 10 − 4 + 3 − 1 10 − 4 ) = 28 |A_1|=\binom{10-4+3-1}{10-4}=28 ∣A1∣=(10−410−4+3−1)=28
类似的有 ∣ A 2 ∣ = ( 10 − 5 + 3 − 1 10 − 5 ) = 21 , ∣ A 3 ∣ = ( 10 − 6 + 3 − 1 10 − 6 ) = 15 |A_2|=\binom{10-5+3-1}{10-5}=21,|A_3|=\binom{10-6+3-1}{10-6}=15 ∣A2∣=(10−510−5+3−1)=21,∣A3∣=(10−610−6+3−1)=15
∣ A 1 ∩ A 2 ∣ = ( 10 − 5 − 4 + 3 − 1 10 − 5 − 4 ) = 3 , ∣ A 1 ∩ A 3 ∣ = ( 10 − 4 − 6 + 3 − 1 10 − 4 − 6 ) = 1 , ∣ A 2 ∩ A 3 ∣ = 0 ∣ A 1 ∩ A 2 ∩ A 3 ∣ = 0 |A_1\cap A_2|=\binom{10-5-4+3-1}{10-5-4}=3,|A_1\cap A_3|=\binom{10-4-6+3-1}{10-4-6}=1,|A_2\cap A_3|=0\\|A_1\cap A_2\cap A_3|=0 ∣A1∩A2∣=(10−5−410−5−4+3−1)=3,∣A1∩A3∣=(10−4−610−4−6+3−1)=1,∣A2∩A3∣=0∣A1∩A2∩A3∣=0
而a的个数小于等于3,b的个数小于等于4,c的个数小于等于5的10组合全体为
∣ A 1 ‾ ∩ A 2 ‾ ∩ A 3 ‾ ∣ = ∣ A ∣ − ( ∣ A 1 ∣ + ∣ A 2 ∣ + ∣ A 3 ∣ ) + ( ∣ A 1 ∩ A 2 ∣ + ∣ A 1 ∩ A 3 ∣ + ∣ A 2 ∩ A 3 ∣ ) − ∣ A 1 ∩ A 2 ∩ A 3 ∣ = 66 − ( 28 + 21 + 15 ) + ( 3 + 1 + 0 ) − 0 = 6 |\overline{A_1}\cap \overline{A_2} \cap \overline{A_3} |=|A|-(|A_1|+|A_2|+|A_3|)+(|A1\cap A2| + |A1\cap A3| + |A2\cap A3|)-|A_1\cap A_2\cap A_3|=66-(28+21+15)+(3+1+0)-0=6 ∣A1∩A2∩A3∣=∣A∣−(∣A1∣+∣A2∣+∣A3∣)+(∣A1∩A2∣+∣A1∩A3∣+∣A2∩A3∣)−∣A1∩A2∩A3∣=66−(28+21+15)+(3+1+0)−0=6
错排问题
集合{1, 2, …, n}的一个错排是该集合的一个满足条件 i j ≠ j i_j ≠ j ij=j 的全排列 i 1 i 2 … i n i_1i_2…i_n i1i2…in,即集合{1, 2, …, n}的没有一个数字在它的自然顺序位置上的全排列.记为 D n D_n Dn
其中 D 1 = 0 , D 2 = 1 , D 3 = 2 , D 4 = 9 D_1=0, D_2=1, D_3=2, D_4=9 D1=0,D2=1,D3=2,D4=9
定理 2.1:错排递推关系 D n = ( n − 1 ) ( D n − 1 + D n − 2 ) = n D n − 1 + ( − 1 ) n = n ! ( 1 − 1 1 ! + 1 2 ! − 1 3 ! + . . . + ( − 1 ) n 1 n ! ) D_n=(n-1)(D_{n-1}+D_{n-2})\\=nD_{n-1}+(-1)^n\\=n!(1-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+...+(-1)^n\frac{1}{n!}) Dn=(n−1)(Dn−1+Dn−2)=nDn−1+(−1)n=n!(1−1!1+2!1−3!1+...+(−1)nn!1)
用 Q n Q_n Qn 表示 {1,2,…,n} 的不出现 12,23,…,(n – 1)n 这些模式的全排列的个数,并规定 Q 1 = 1 Q_1 = 1 Q1=1
定理 2.2:有禁止的排列关系 Q n = n ! − ( n − 1 1 ) ( n − 1 ) ! + ( n − 1 2 ) ( n − 2 ) ! − . . . + ( − 1 ) n − 1 ( n − 1 n − 1 ) 1 ! Q_n=n!-\binom{n-1}{1}(n-1)!+\binom{n-1}{2}(n-2)!-...+(-1)^{n-1}\binom{n-1}{n-1}1! Qn=n!−(1n−1)(n−1)!+(2n−1)(n−2)!−...+(−1)n−1(n−1n−1)1!
3. 鸽巢原理
如果鸽子的数目比巢穴的数目多,那么至少要有一个鸽巢被两只或多只鸽子占据。
如果把 n + 1 个物体放入 n 个盒子,那么至少有一个盒子中有两个或更多的物品。
若把 n (r – 1) + 1 个物体放入 n 个盒子,那么至少有一个盒子中有 r 个物品。
4. Ramsey 定理
任何 6 个人的聚会,其中总会有 3 个人互相认识或 3 个人互相不认识。
定理 4.1:对于任意给定的两个正整数 a 和 b,如果存在最小的正整数 r (a, b)
使得当 N ≥ r (a, b)时,对 K N K_N KN 任意进行红、蓝两边着色, K N K_N KN 中均有红色 K a K_a Ka,或蓝色 K b K_b Kb则 r (a, b)称为 Ramsey 数
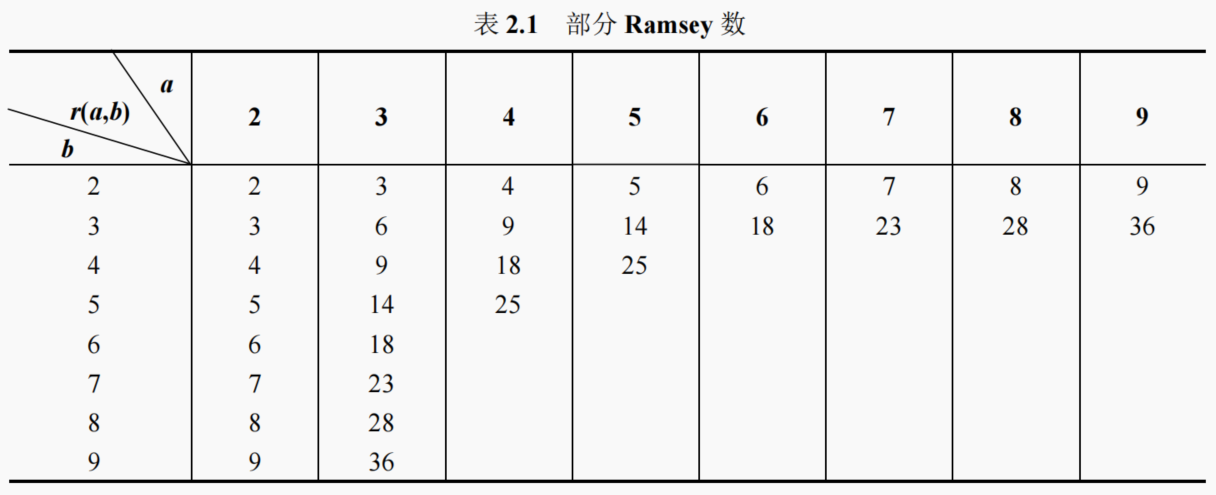
定理 4.2:对任意正整数 a,b,有 r(a, b) = r(b, a);r(a, 2) = a
对任意正整数 a ≥ 3,b ≥ 3,有 r(a, b) ≤ r(a – 1, b) + r(a, b–1)
对任意正整数 a ≥ 2,b ≥ 2,有 r(a, b) ≤ ( a + b − 2 a − 1 ) \binom{a+b-2}{a-1} (a−1a+b−2)
作业习题链接:作业 第二章 鸽巢原理
相关文章:

【组合数学】容斥鸽巢原理
目录 1. 容斥原理容斥原理三种形式 2. 容斥原理应用有限重复数的多重集合的 r 组合数错排问题 3. 鸽巢原理4. Ramsey 定理 1. 容斥原理 容斥原理提供了一种通过计算每个单独集合的大小,然后修正重复计数的方法,从而得到多个集合并集大小的计算方法。它通…...
视频后期特效处理软件 Motion 5 mac中文版
Motion mac是一款运动图形和视频合成软件,适用于Mac OS平台。 Motion mac软件特点 - 精美的效果:Motion提供了多种高质量的运动图形和视频效果,例如3D效果、烟雾效果、粒子效果等,方便用户制作出丰富多彩的视频和动画。 - 高效的工…...

【智能家居】一、工厂模式实现继电器灯控制
用户手册对应的I/O 工厂模式实现继电器灯控制 代码段 controlDevice.h(设备设备)main.c(主函数)bathroomLight.c(浴室灯)bedroomLight.c(卧室灯)restaurantLight.c(餐厅…...
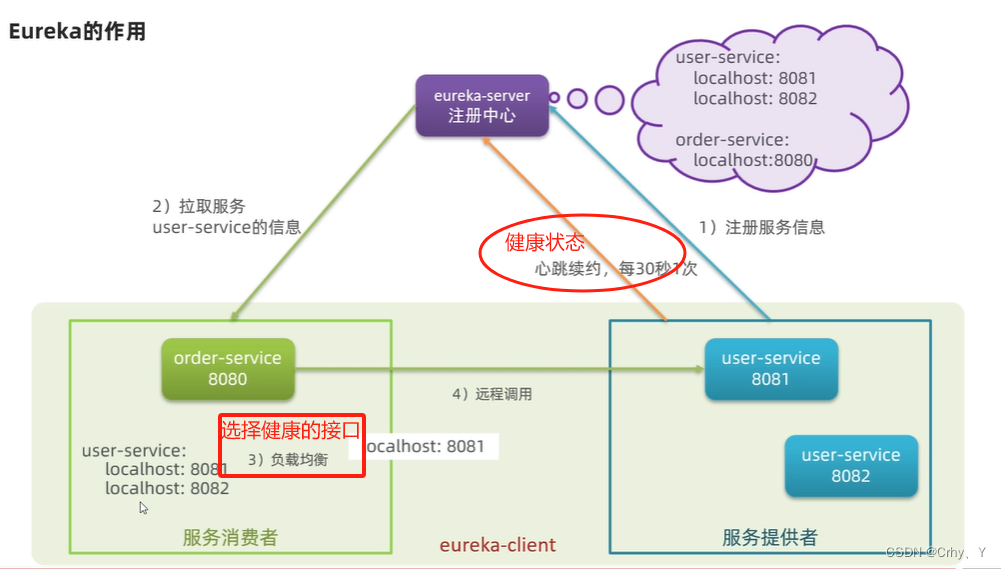
第三节:提供者、消费者、Eureka
一、 提供者 消费者(就是个说法、定义,以防别人叭叭时听不懂) 服务提供者:业务中被其他微服务调用的服务。(提供接口给其他服务调用)服务消费者:业务中调用其他微服务的服务。(调用…...
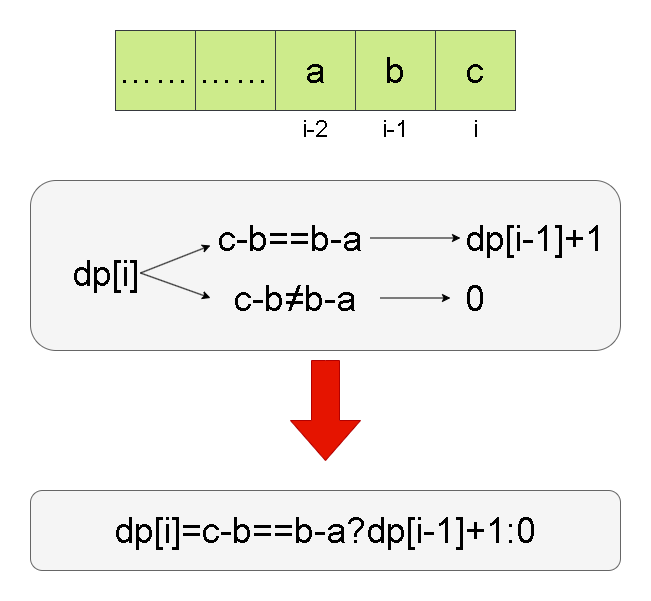
Leetcode刷题详解——等差数列划分
1. 题目链接:413. 等差数列划分 2. 题目描述: 如果一个数列 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该数列为等差数列。 例如,[1,3,5,7,9]、[7,7,7,7] 和 [3,-1,-5,-9] 都是等差数列。 给你一个整数数组 …...

导出主机上所有docker 镜像并导入到其它主机
保存镜像列表到文件 docker images --format “{{.Repository}}:{{.Tag}}” > image_list.txt 导出列表中所有镜像到tar文件 cat image_list.txt | xargs -L 1 docker save -o all_images.tar 导入tar包中所有镜像 docker load -i all_images.tar...

HTML5+CSS3+JS小实例:焦点图波浪切换动画特效
实例:焦点图波浪切换动画特效 技术栈:HTML+CSS+JS 字体图标库:Font Awesome 效果: 源码: 【HTML】 <!DOCTYPE html> <html><head><meta http-equiv="content-type" content="text/html; charset=utf-8"><meta name=&…...
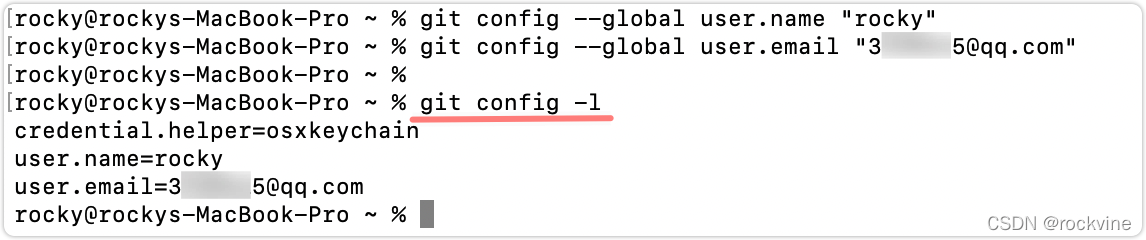
Mac电脑如何安装git
一、简介 在Mac上安装Git之前,可以先使用git --version来查看一下是否安装了Git,因为Mac系统可能自带了Git,或者在你安装XCode(或者XCode的命令行工具)时,可能已经安装了 Git。 如果Mac还没有安装Git的话&…...
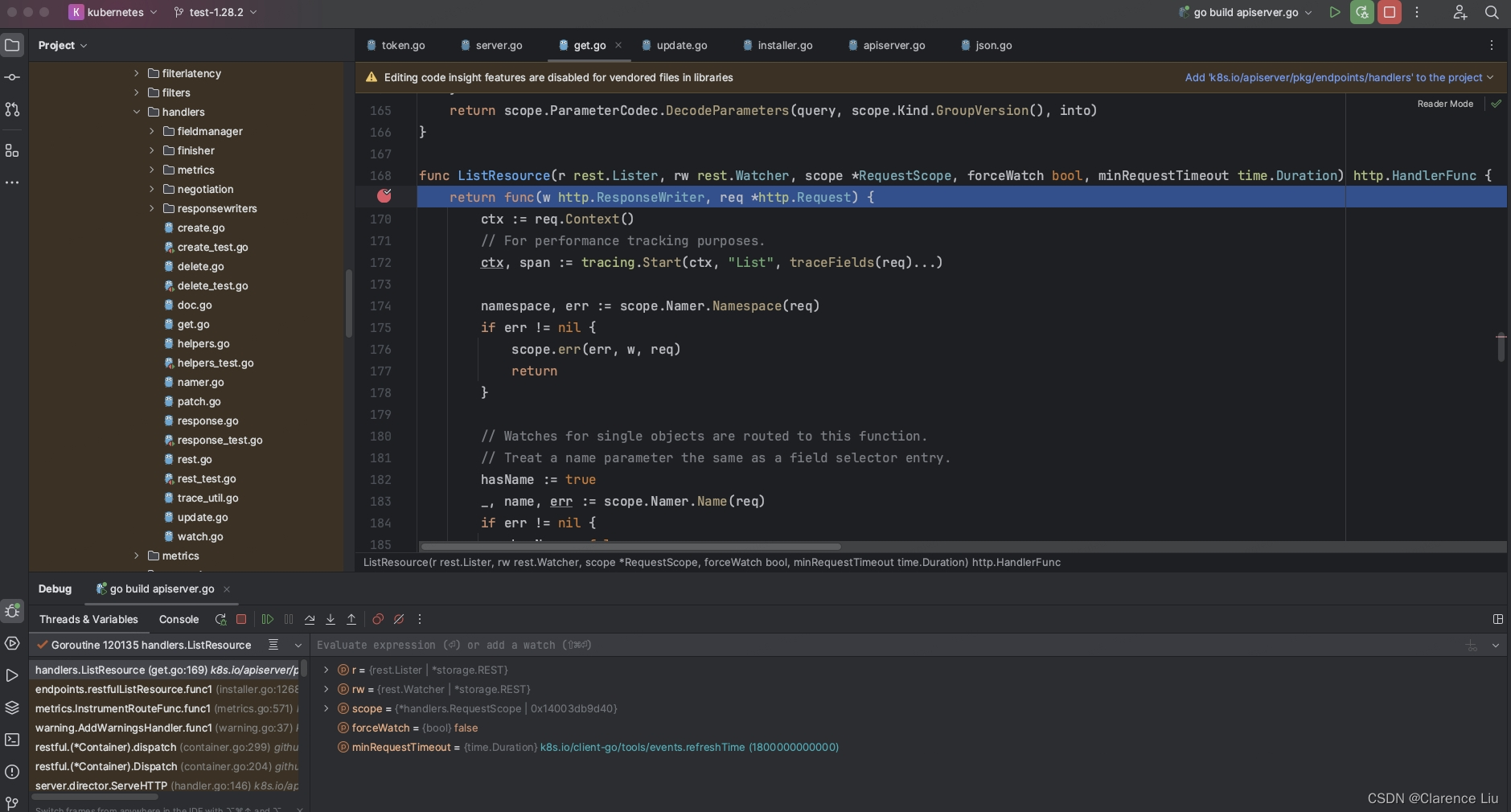
macOS本地调试k8s源码
目录 准备工作创建集群注意点1. kubeconfig未正常加载2. container runtime is not running3. The connection to the server 172.16.190.132:6443 was refused - did you specify the right host or port?4. 集群重置5.加入子节点 代码调试 准备工作 apple m1芯片 安装vmwa…...

JS 实现一键复制文本内容
1、演示: 2、代码 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>一键复制</title&g…...

【Linux】echo命令使用
echo命令 功能是在显示器上显示一段文字,一般起到一个提示的作用。此外,也可以直接在文件中写入要写的内容。也可以用于脚本编程时显示某一个变量的值,或者直接输出指定的字符串。 著者 由布莱恩福克斯和切特拉米撰写。 语法 echo […...

Day03 嵌入式---中断
目录 一、简单介绍 二、总体框架 三、NVIC 3.2 NVIC的寄存器 3.3 中断向量表 3.4 中断优先级 3.5 NVIC优先级分组 3.6 NVIC配置 3.6.1、设置中断分组 3.6.2、初始化 四、EXTI 外部中断 4.1.EXTI的基本概念 4.2.EXTI的⼯作原理 4.3 EXTI配置 五、SYSCFG 5.1 SYS…...
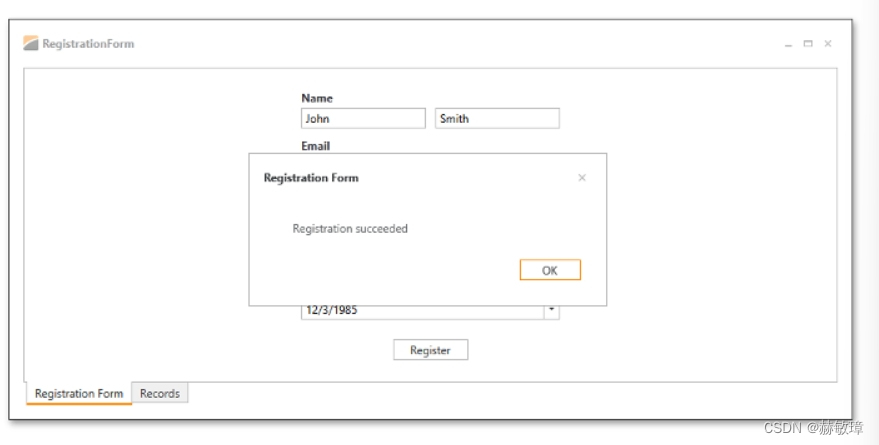
wpf devexpress 使用IDataErrorInfo实现input验证
此处下载源码 当form初始化显示,Register按钮应该启动和没有输入错误应该显示。如果用户点击注册按钮在特定的输入无效数据,form将显示输入错误和禁用的注册按钮。实现逻辑在标准的IDataErrorInfo接口。请查阅IDataErrorInfo接口(System.Com…...

shell_81.Linux在命令行中创建使用函数
在命令行中使用函数 在命令行中创建函数 两种方法 单行方式来定义函数: $ function divem { echo $[ $1 / $2 ]; } $ divem 100 5 20 $ 当你在命令行中定义函数时,必须在每个命令后面加个分号,这样 shell 就能知道哪里是命令的起止了&am…...
)
鱼香ROS一键安装命令(支持微信、docker、ros等)
按照指定的数字选择即可。 wget http://fishros.com/install -O fishros && . fishros小鱼的一键安装系列 [14个ROS版本任你选]一键安装Docker使用指南...

深入理解 Go 函数:从基础到高级
一、函数基础 1、函数定义 函数是组织好的、可重复使用的、用于执行指定任务的代码块Go 语言中支持:函数、匿名函数和闭包 package mainimport "fmt"func main(){ret : intSum(1,2)fmt.PrintIn(ret) //3 }func instSum(x,y int) int {return x y }…...
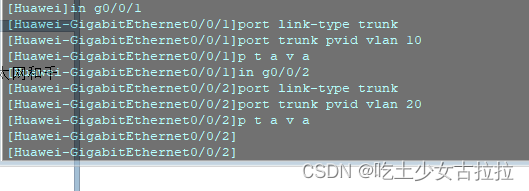
开启三层交换机DHCP服务
二层交换机上不需要配置任何东西,只需要在pc机上开启dhcp服务,配置好LSW1后就可以自动获取到IP地址。 sys Enter system view, return user view with CtrlZ. [Huawei]sys sw1 [sw1]dhcp enable Info: The operation may take a few seconds. Please wai…...

jspdf+html2canvas浏览器缩放问题
之前在弄页面导出为pdf的时候,jspdf配合html2canvas貌似很好用,我自己在使用的时候也没有觉得有什么问题,但是客户那边反馈说下载下来的pdf不全. 后来问了客户才发现客户的浏览器比例缩放到了125%;这就导致了pdf不全, 先看看原来的代码: download() {let jsPDF jspdf.jsPDF;l…...

西南科技大学模拟电子技术实验六(BJT电压串联负反馈放大电路)预习报告
一、计算/设计过程 BJT电压串联负反馈放大电路图1-1-1-1为BJT电压串联负反馈放大实验电路,若需稳定输出电压,减小从信号源所取电流,可引入电压串联负反馈闭合开关。 图1-1-1-1 理论算法公式(1)闭环电压放大倍数 (2)反馈系数 (3)输入电阻 (4)输出电阻 计算过程。开环…...

JS的监听事件
在JavaScript中,你可以使用监听器来捕获和处理不同类型的事件。通过添加事件监听器,你可以指定当特定事件发生时要执行的函数。 以下是几种常见的监听事件的方法: 1. addEventListener():用于在目标元素上添加事件监听器。它接受…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...
