L1-009:N个数求和
目录
⭐题目描述⭐
⭐分析
⭐程序代码
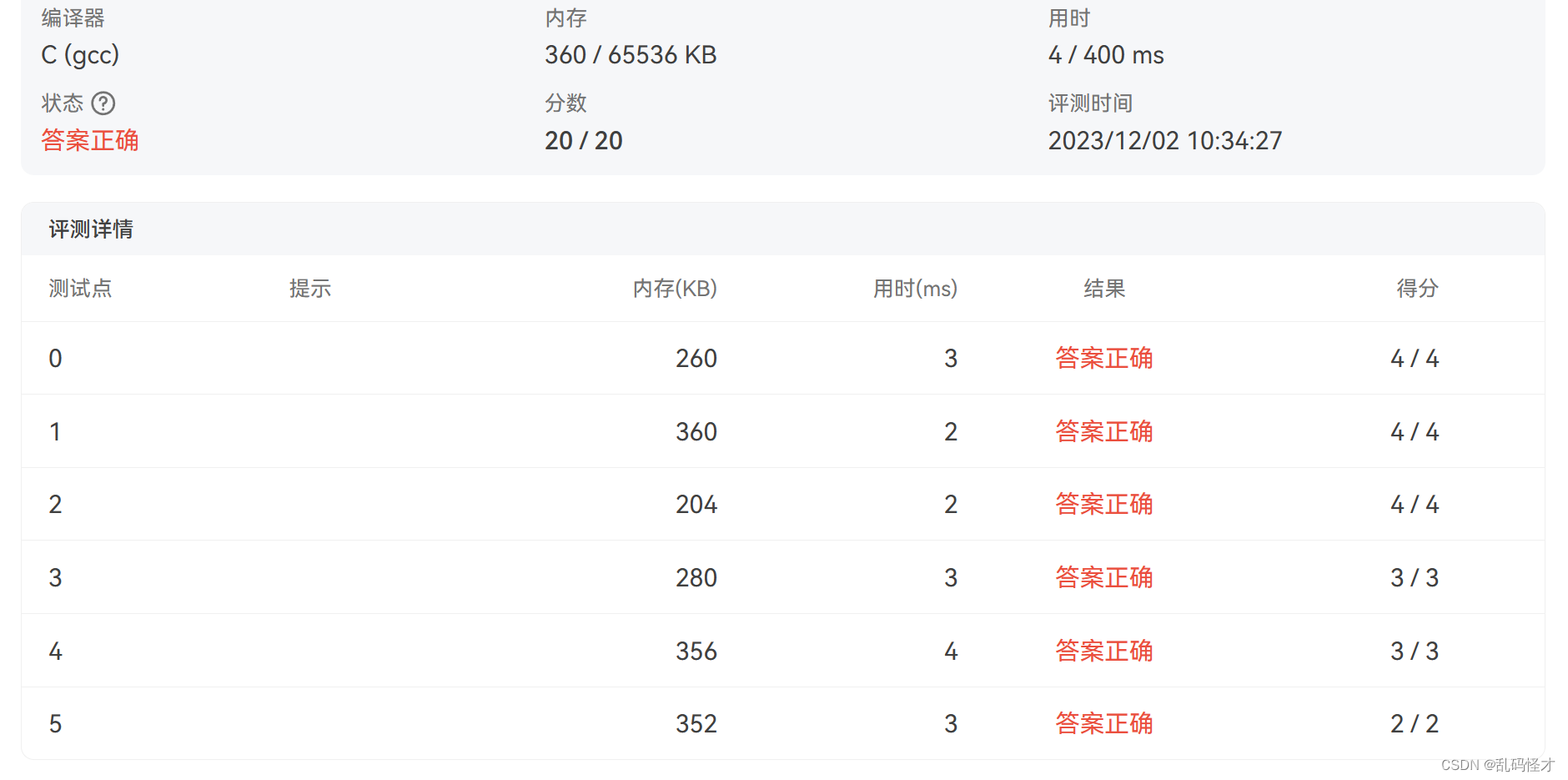
运行结果
⭐文案分享⭐
⭐题目描述⭐
本题的要求很简单,就是求
N个数字的和。麻烦的是,这些数字是以有理数分子/分母的形式给出的,你输出的和也必须是有理数的形式。
输入格式:
输入第一行给出一个正整数
N(≤100)。随后一行按格式a1/b1 a2/b2 ...给出N个有理数。题目保证所有分子和分母都在长整型范围内。另外,负数的符号一定出现在分子前面。
输出格式:
输出上述数字和的最简形式 —— 即将结果写成
整数部分 分数部分,其中分数部分写成分子/分母,要求分子小于分母,且它们没有公因子。如果结果的整数部分为0,则只输出分数部分。
输入样例1:
5 2/5 4/15 1/30 -2/60 8/3输出样例1:
3 1/3输入样例2:
2 4/3 2/3输出样例2:
2输入样例3:
3 1/3 -1/6 1/8输出样例3:
7/24
⭐分析
我们可以用两个变量sum和num来计算分子和分母的变化,一开始我们将sum的值赋为0,num的值赋为1,然后字母a为输入分数的分子,b为分母,以样例测试一为例:
5 2/5 4/15 1/30 -2/60 8/3算法描述为:
for(int i=0;i<N;i++){scanf("%d/%d",&a,&b);sum*=b;sum+=num*a;num*=b;int s=num_GY(num,sum);//寻找num和sum的最大公约数sum=sum/s;//将分子和分母最简化num=num/s;}
sum=0 a num=1 b sum=0*5=0
sum=0+1*2=2
2 num=1*5=5 5 sum=2/1=2 sum和num的最大公约数为1 num=5/1=5 sum和num的最大公约数为1 sum=2*15=30
sum=30+5*4=50
4 num=5*15=75 15 sum=50/25=2 sum和num的最大公约数为25 num=75/25=3 sum和num的最大公约数为25 sum=2*30=60
sum=60+3*1=63
1 num=3*30=90 30 sum=63/9=7 sum和num的最大公约数为9 num=90/9=10 sum和num的最大公约数为9 sum=7*60=420
sum=420+10*(-2)=400
-2 num=10*60=600 60 sum=400/200=2 sum和num的最大公约数为200 num=600/200=3 sum和num的最大公约数为200 sum=2*3=6
sum=6+3*8=30
8 num=3*3=9 3 sum=30/3=10 sum和num的最大公约数为3 num=9/3=3 sum和num的最大公约数为3
求两个数的最大公约数,我们可以用辗转相除法,这样我们的程序的时间复杂度是O(n),如果我们在写算法题的过程中遇到超时问题,请先检查我们的算法是否有循环套循环的过程,如果有,请想办法去掉一层循环来降低我们的算法时间复杂度。
辗转相除法的算法描述:
int num_GY(int num,int sum){//寻找分子分母的最大公约数int min=num<sum?num:sum;//找出两个数的最小值int max=num>sum?num:sum;//找出两个数的最大值int t;while(min!=0){//利用辗转相除法计算最大公约数t=max%min;max=min;min=t;}return max; }举例:
我们可以任意找两个数,比如63和90,我们来用辗转相除法求最大公约数。
首先我们先判断出这两个数的最大值和最小值。
int min=num<sum?num:sum;//找出两个数的最小值 int max=num>sum?num:sum;//找出两个数的最大值
循环 t max=90 min=63 第一次循环(min!=0) t=90%63=27 max=63 min=27 第二次循环(min!=0) t=63%27=9 max=27 min=9 第三次循环(min!=0) t=27%9=0 max=9 min=0 第四次循环(min==0) 退出循环 返回max=9 结束
⭐程序代码
#include<stdio.h>
int num_GY(int num,int sum){//寻找分子分母的最大公约数int min=num<sum?num:sum;//找出两个数的最小值int max=num>sum?num:sum;int t;while(min!=0){//利用辗转相除法计算最大公约数t=max%min;max=min;min=t;}return max;
}
int main(){int N;scanf("%d",&N);int a,b;int sum=0,num=1;//sum为分子和,num为分母和for(int i=0;i<N;i++){scanf("%d/%d",&a,&b);sum*=b;sum+=num*a;num*=b;int s=num_GY(num,sum);sum=sum/s;//将分子和分母最简化num=num/s;}if(sum%num==0)//当分子是分母的倍数时printf("%d",sum/num);else if(sum<num)//当分子小于分母时printf("%d/%d",sum,num);else//当分子大于分母时printf("%d %d/%d",sum/num,sum%num,num);return 0;
}💖运行结果💖
⭐文案分享⭐
永远相信美好的事情即将发生。--------2023.12.2💖
相关文章:

L1-009:N个数求和
目录 ⭐题目描述⭐ ⭐分析 ⭐程序代码 运行结果 ⭐文案分享⭐ ⭐题目描述⭐ 本题的要求很简单,就是求N个数字的和。麻烦的是,这些数字是以有理数分子/分母的形式给出的,你输出的和也必须是有理数的形式。 输入格式: 输入第一行给出…...
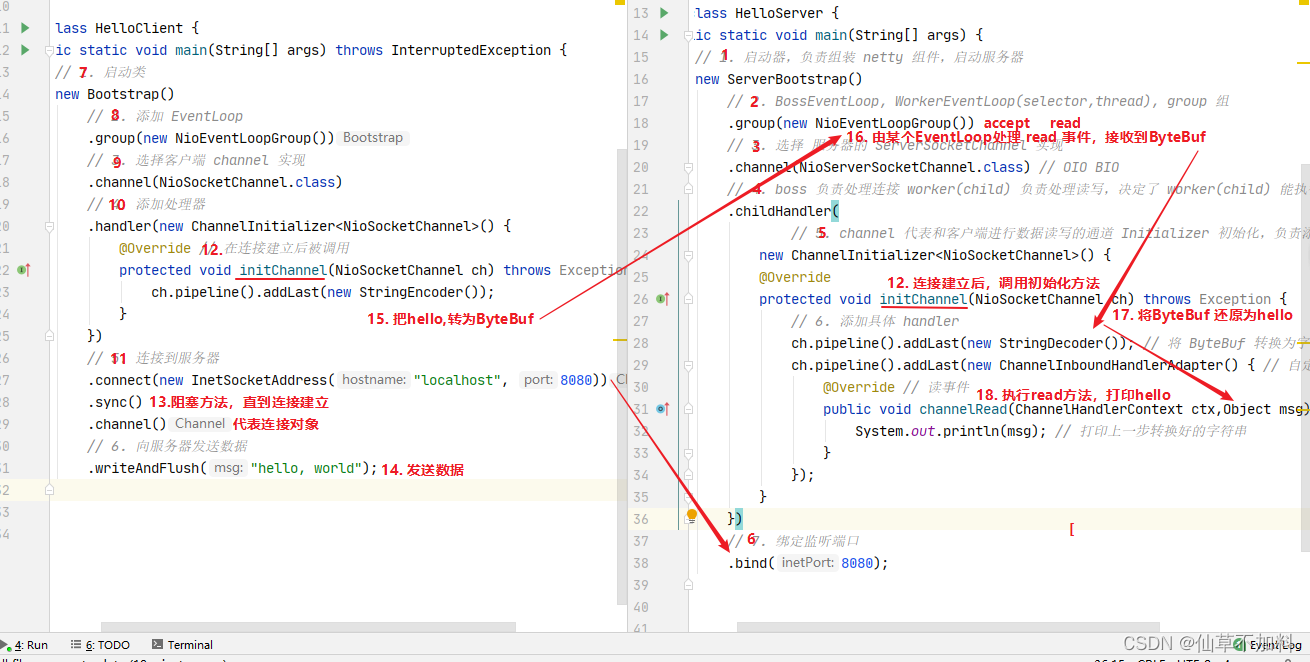
当发送“Hello,World”时,channel发生了什么?
一、Netty概述 1.Netty是什么? Netty 是一个异步的、基于事件驱动的网络应用框架,用于快速开发可维护、高性能的网络服务器和客户端。 2.Netty的地位怎么样? Netty 在 Java 网络应用框架中的地位就好比:Spring 框架在 JavaEE …...
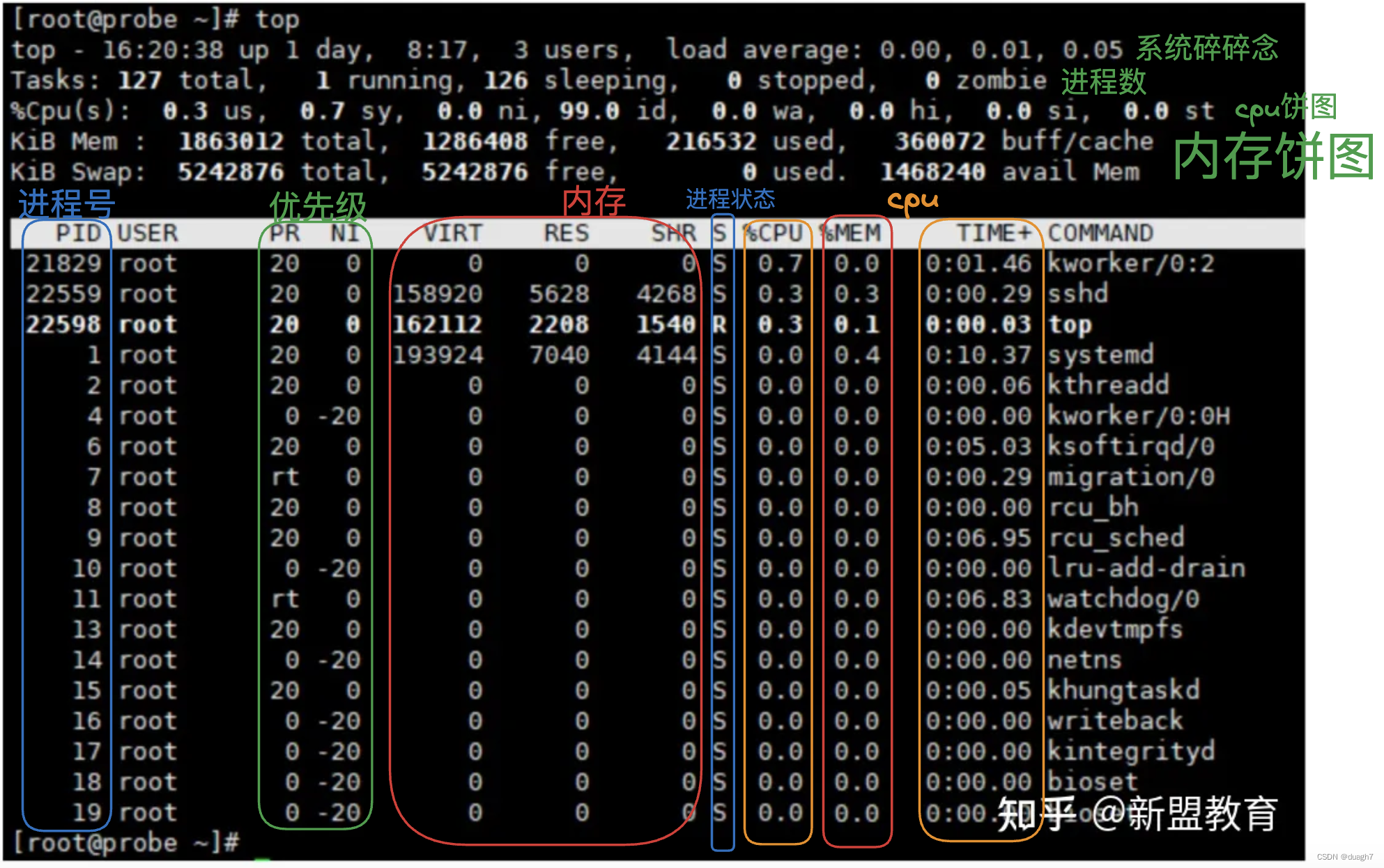
服务器运行情况及线上排查问题常用命令
一、top命令 指令行: top返回: 返回分为两部分 (一)系统概览,见图知意 以下是几个需要注意的参数 1、load average: 系统负载,即任务队列的平均长度。三个数值分别为 1分钟、5分钟、15分…...

Hadoop学习笔记(HDP)-Part.18 安装Flink
目录 Part.01 关于HDP Part.02 核心组件原理 Part.03 资源规划 Part.04 基础环境配置 Part.05 Yum源配置 Part.06 安装OracleJDK Part.07 安装MySQL Part.08 部署Ambari集群 Part.09 安装OpenLDAP Part.10 创建集群 Part.11 安装Kerberos Part.12 安装HDFS Part.13 安装Ranger …...

LeetCode56. 合并区间
🔗:【贪心算法,合并区间有细节!LeetCode:56.合并区间-哔哩哔哩】 class Solution { public:vector<vector<int>> merge(vector<vector<int>>& intervals) {if(intervals.size()0){return intervals;…...
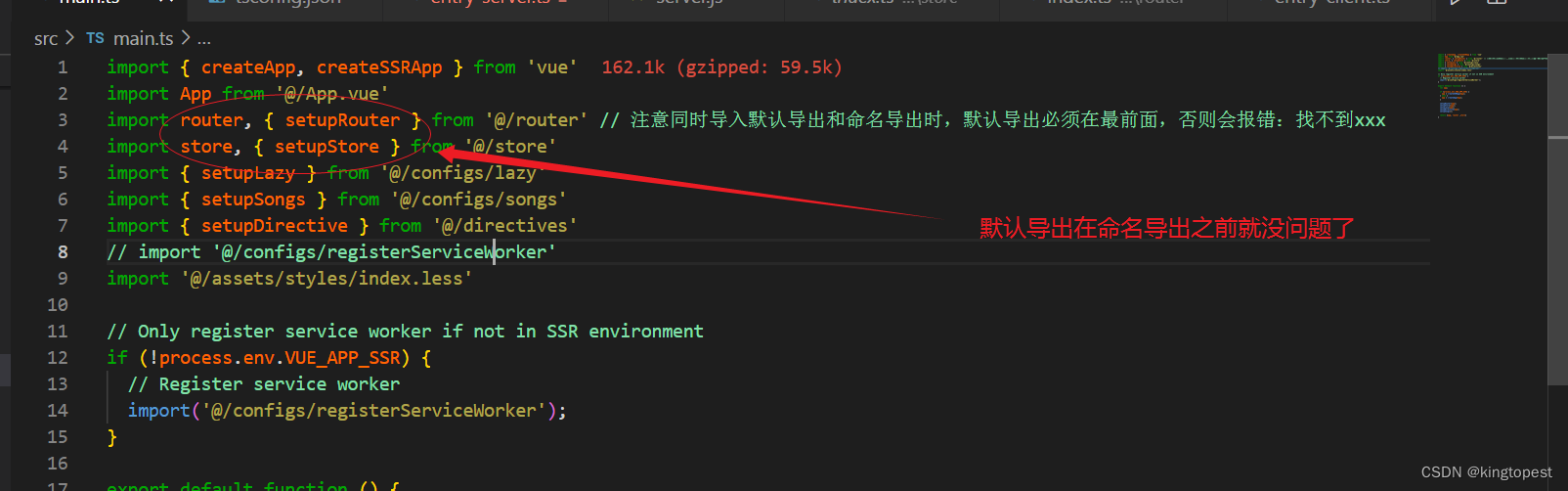
解决typescript报错:找不到名称xxx
现象: 原因:在同时导入默认导出和命名导出时,默认导出必须放在命名导出之前 下面的就是原始文件: 默认导出指: export default导出类型, import时无需大括号 命名导出指: 仅有export关键字…...
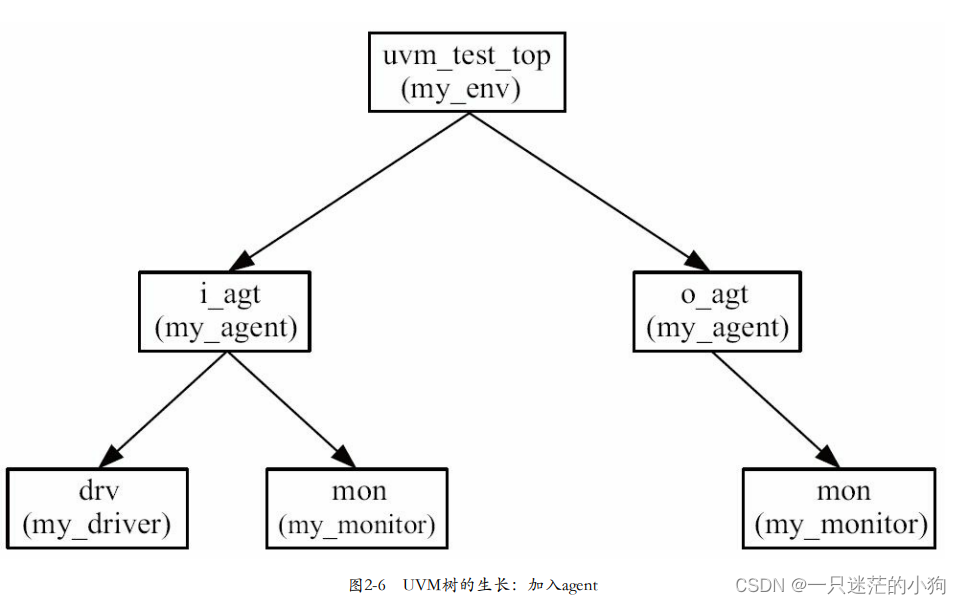
UVM中封装成agent
在验证平台中加入monitor时,看到driver和monitor之间的联系:两者之间的代码高度相似。其本质是因为二者 处理的是同一种协议,在同样一套既定的规则下做着不同的事情。由于二者的这种相似性,UVM中通常将二者封装在一起,…...
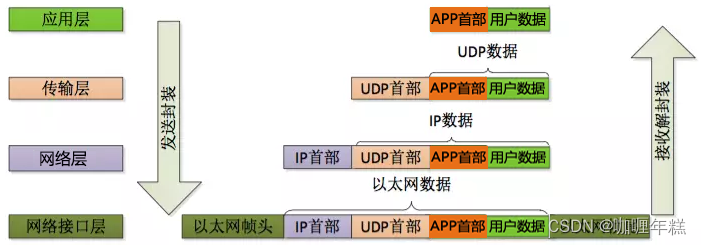
OSI七层模型与TCP/IP四层模型
一、OSI七层模型简述 OSI 模型的七层是什么?在 OSI 模型中如何进行通信?OSI 模型有哪些替代方案? TCP/IP 模型关于专有协议和模型的说明 二、七层模型详解(DNS、CDN、OSI) 状态码DNS nslookup命令 CDN whois命令 …...
QT 中 QProgressDialog 进度条窗口 备查
基础API //两个构造函数 QProgressDialog::QProgressDialog(QWidget *parent nullptr, Qt::WindowFlags f Qt::WindowFlags());QProgressDialog::QProgressDialog(const QString &labelText, const QString &cancelButtonText, int minimum, int maximum, QWidget *…...
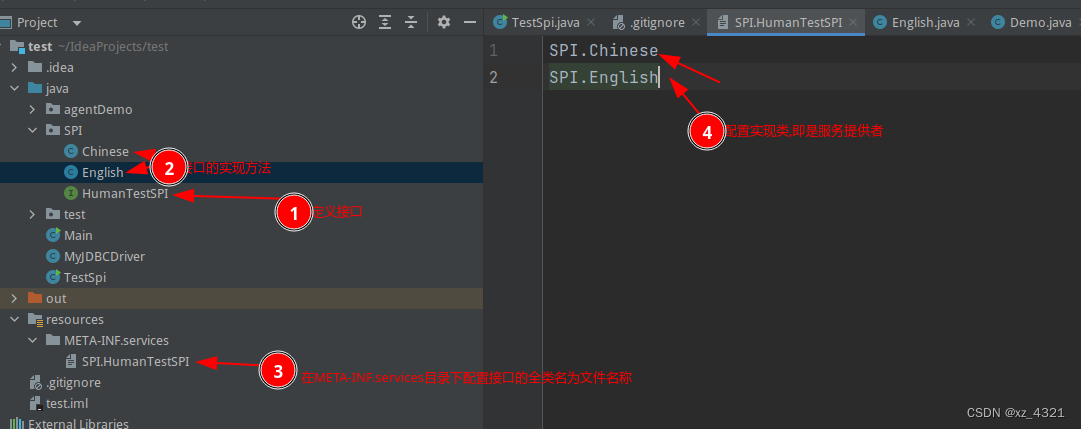
学习ShardingSphere前置知识
学习ShardingSphere前置准备知识 一. SPI SPI(Service Provider Interface)是一种Java的扩展机制,用于实现组件之间的松耦合。在SPI模型中,服务提供者(Service Provider)定义了一组接口,而服务…...
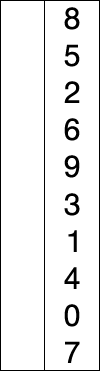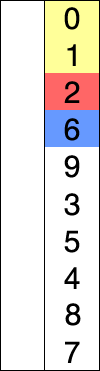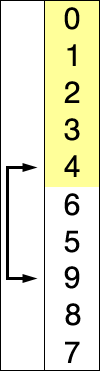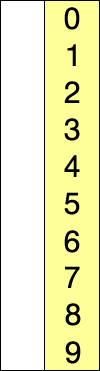
读书笔记-《数据结构与算法》-摘要3[选择排序]
选择排序 核心:不断地选择剩余元素中的最小者。 找到数组中最小元素并将其和数组第一个元素交换位置。在剩下的元素中找到最小元素并将其与数组第二个元素交换,直至整个数组排序。 性质: 比较次数(N-1)(N-2)(N-3)…21~N^2/2交换次数N运行…...
)
Arduino驱动MLX90614红外测温传感器(温湿度传感器)
目录 1、传感器特性 2、测量方法 3、硬件原理图 4、控制器和传感器连线图...

Ubuntu上传文件到SMB共享文件夹
0. 前言 公司有一些数据共享文件夹,平时可以把开发的重要文件放到上面备份。本人开发使用ubuntu系统,共享文件夹是windows的形式,想通过命令的方式,方便快捷,还可shell脚本自动化。 1. 安装挂载库 sudo apt-get upd…...

【Linux】基础IO--重定向理解Linux下一切皆文件缓冲区
文章目录 一、重定向1.什么是重定向2.dup2 系统调用3.理解输入重定向、输出重定向和追加重定向4.简易shell完整实现 二、理解linux下一切皆文件三、缓冲区1.为什么要有缓冲区2.缓冲区的刷新策略3.缓冲区的位置4.实现一个简易的C语言缓冲区5.内核缓冲区 一、重定向 1.什么是重定…...

RINEX介绍
一、RINEX是什么 Receiver Independent Exchange Format (RINEX) 是一种用于存储、交换和处理全球定位系统 (GPS) 接收机观测数据的标准化文件格式。RINEX 格式由国际电信联盟 (ITU) 和国际GPS服务 (IGS) 组织共同开发和维护。它提供了一种通用的数据格式,使得不同…...

ROS-ROS通信机制-服务通信
文章目录 一、服务通信基本知识二、自定义srv三、C实现四、Python实现 一、服务通信基本知识 服务通信也是ROS中一种极其常用的通信模式,服务通信是基于请求响应模式的,是一种应答机制。也即: 一个节点A向另一个节点B发送请求,B接收处理请求…...
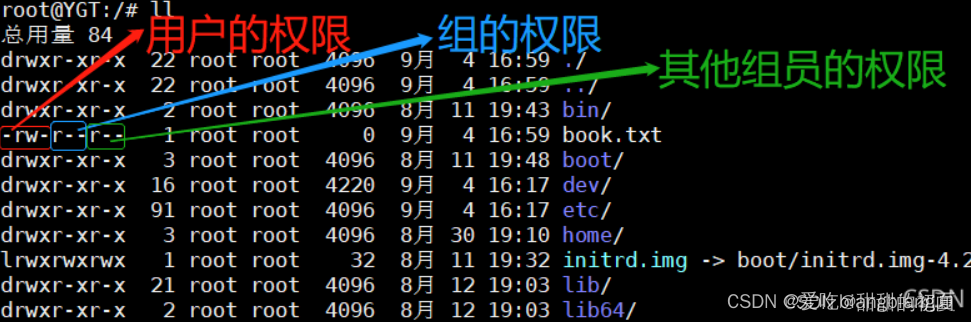
chown和chmod
chown和chmod都是在Linux和Unix系统中用于设置文件和文件夹权限的命令,但它们的功能和用途有所不同。 功能:chown主要用于修改文件或文件夹的所有者和所属组,而chmod则主要用于修改文件或文件夹的读写执行权限。用途:如果想要授权…...

【GPU】linux 安装、卸载 nvidia 显卡驱动、cuda 的官方文档、推荐方式(runfile)
文章目录 1. 显卡驱动1.1. 各版本下载地址1.2. 各版本文档地址1.3. 安装、卸载方式 2. CUDA2.1. 各版本下载地址2.2. 各版本文档地址2.3. 安装、卸载方式2.4. 多版本 CUDA 切换方式 1. 显卡驱动 1.1. 各版本下载地址 https://www.nvidia.com/Download/Find.aspx?langzh-cn 1…...
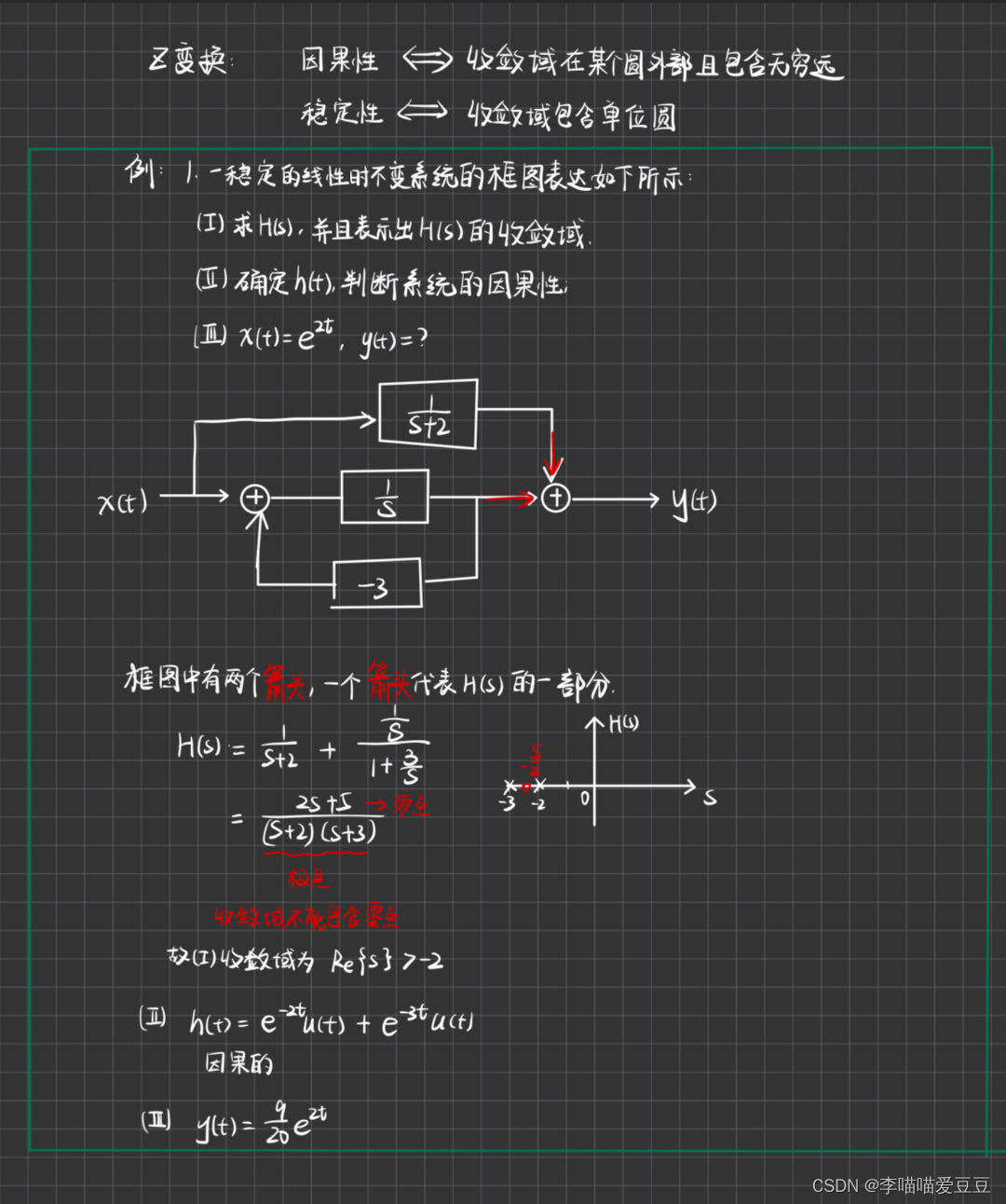
6页手写笔记总结信号与系统常考知识大题知识点
题型一 判断系统特性题型二 求系统卷积题型三 求三大变换正反变换题型四 求全响应题型五 已知微分方程求系统传递函数题型六 已知系统的传递函数求微分方程题型七 画出系统的零极点图,并判断系统的因果性和稳定性 (笔记适合快速复习,可能会有…...

Qt-QSplitter正确设置比例
简短版本: splitter->setSizes({1000, 2000}); // 这个值至少跟像素值设置的一样大,或者更大,例如x10倍详细版本: setSizes 官方介绍如下: Sets the child widgets’ respective sizes to the values given in the…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...

跨平台商品数据接口的标准化与规范化发展路径:淘宝京东拼多多的最新实践
在电商行业蓬勃发展的当下,多平台运营已成为众多商家的必然选择。然而,不同电商平台在商品数据接口方面存在差异,导致商家在跨平台运营时面临诸多挑战,如数据对接困难、运营效率低下、用户体验不一致等。跨平台商品数据接口的标准…...
