Multidimensional Scaling(MDS多维缩放)算法及其应用
在这篇博客中,我将与大家分享在流形分析领域的一个非常重要的方法,即多维缩放MDS。整体来说,该方法提供了一种将内蕴距离映射到显性欧氏空间的计算,为非刚性形状分析提供了一种解决方案。当初就是因为读了Bronstein的相关工作【1】,才下定决心在人脸数据分析中使用内蕴度量来建立特征分析方法,可以说MDS对我的学术之路起到了很大的影响作用。
1. 前言
在非刚性形状匹配中,我们希望找到两个曲面的对应关系。由于受到非刚性形变影响,使得我们不能直接建立基于类似ICP一样的方法来实现对准。提到非刚性分析,很自然的就会让人联想到使用基于曲面第一基本形式的内蕴几何特征来建立分析方法。对于人脸人体这种非刚性形变分析对象,由于受到骨架的约束,使得其非刚性形变满足近似等距的特性,这里的等距指测地线。曲面第一基本形式对应曲面曲线,刚好可以使用测地线作为表示。那么,我们只要基于测地线来建立几何特征表达,就能够实现近似等距条件下的形状分析,进而满足非刚性形状分析要求。
关于测地线的计算,我在之前的博客已经有所介绍,有兴趣的同学可以翻看:
Fast Marching算法及其在点云测地线计算中的应用-CSDN博客
Geodesic in Heat: 一种测地线计算方法-CSDN博客
在有了测地线作为内蕴几何特征的显性表示后,我们希望对原始曲面建立一种形状度量,这种度量由测地线定义,能够反映形状之间的相似程度,进而推出点的对应关系。一个最直接的想法是利用参数化的方法。通过参数化,我们能够对原始的曲面进行“摊平”,进而在摊平后的参数域建立对应。然而,参数化需要指定边界和控制点,其本身的计算也相对复杂。如果对于拓扑相对复杂的形状建立参数化,其对原始测地线距离将会产生严重扭曲,即不再是可控的近似等距变换。我们希望使用类似ICP那样的直接距离对应方法,对基于测地线表示的曲面进行匹配。一个理想的方案是将点对间的测地距离,变换到一个m维的欧氏空间。在该欧氏空间中,点与点的欧氏距离与未变换前的点对测地距离存在一种对应关系。这样,我们只需要在变换后的形状进行刚性配准,点对的结果就对应了原始数据的非刚性对应结果。这就是使用MDS方法实现非刚性形状分析的初始想法。
2. MDS介绍
如前所述,MDS的目的就是将点间的测地距离嵌入到一个新的欧氏空间中,使得内蕴距离获得显性化的表达。在相关工作【2】中,这种嵌入后的曲面表达被称为bending-invariant canonical forms。具体过程如下:
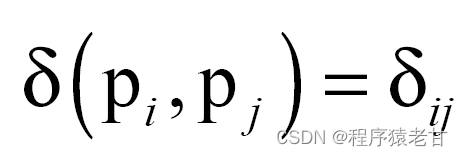
首先我们给出一个测地线的表示δij,表示两点pi和pj的测地距离。我们把所有点的行列组成矩阵形式,使用δij填满,ij相等为0。然后,我们对δij求平方,重写矩阵里的项:
![]()
Δ所表达的矩阵在等距变换下是不变的,但是其形式会因为点序号的变化而变化。我们希望获得一个测地距离不变的表示,且具有唯一性。这时,就可以利用MDS将其嵌入到一个低维的欧氏空间中,该过程等价于:
![]()
嵌入误差可以写为:
![]()
MDS方法也包含很多类别,Bronstein在论文【3】中提到一种称为classical scaling【4】的方法来实现MDS:
![]()
首先对Δ进行中心化操作,即double-centering。J=I-1/2U,I是单位矩阵,U是一个完全由1组成的矩阵。之后对B进行主成分分析,获得对应的m个特征值和特征向量:
![]()
i对应点的序号,j对应m的维度,一般m取3,即将原始形状基于测地距离映射会三维欧氏空间。这样经过特征向量e表达的新坐标x在欧氏空间组成一个新的形状,在工作【1】中被称为Canonical form,以我的观点来看,即内蕴型。
3. 应用
Bronstein在最开始设计算法的时候,目标就是解决三维人脸识别中的表情鲁棒问题。他在论文中已经提到了一般性非刚性形状分析可以转换为对内蕴距离向欧氏空间的嵌入,如下图:
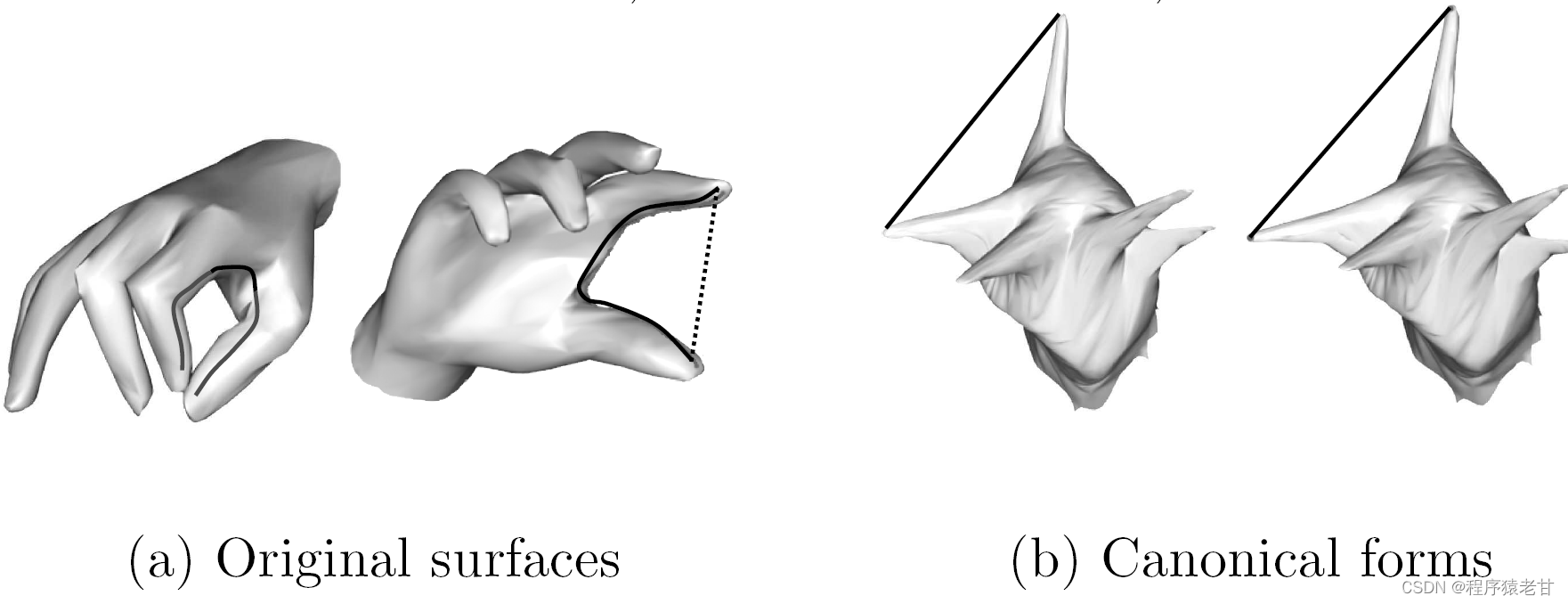
上面的例子充分说明将测地线嵌入回欧氏空间,对应的形状所具备的近似等距特性。原来手指的欧氏距离,一定会因为非刚性形变发生变化,但是对应的测地距离是稳定的。将测地距离嵌入回欧氏空间,得到右边的Canonical form,其点的欧氏距离就具备了原来点的测地距离特性。这时我们再使用类似ICP的方法,就能够非常方便的建立对应关系。
表情即被认为是一种近似等距的非刚性形变,如果我们对人脸数据进行类似Canonical form的变换,那么变换的结果自然会获得对表情不变的结果。原论文中给出了示意图:
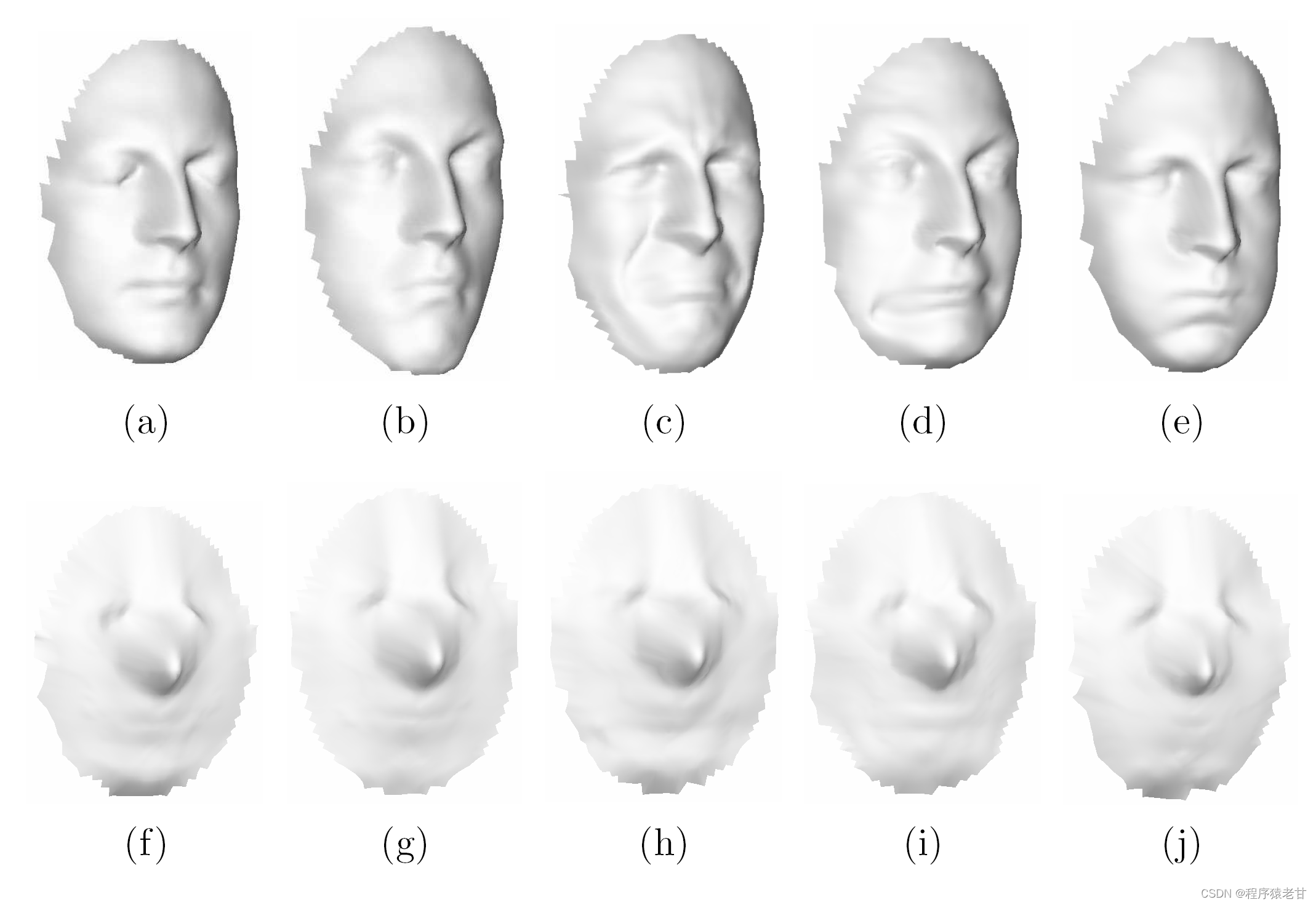
可以看到第一行的人脸是具有多种不同的表情的。但是这些人脸的Canonical form具有极其相近的几何表示。在Canonical form的基础上,设计三维人脸识别算法,自然能获得表情鲁棒特性。论文中还给了一个系统界面:
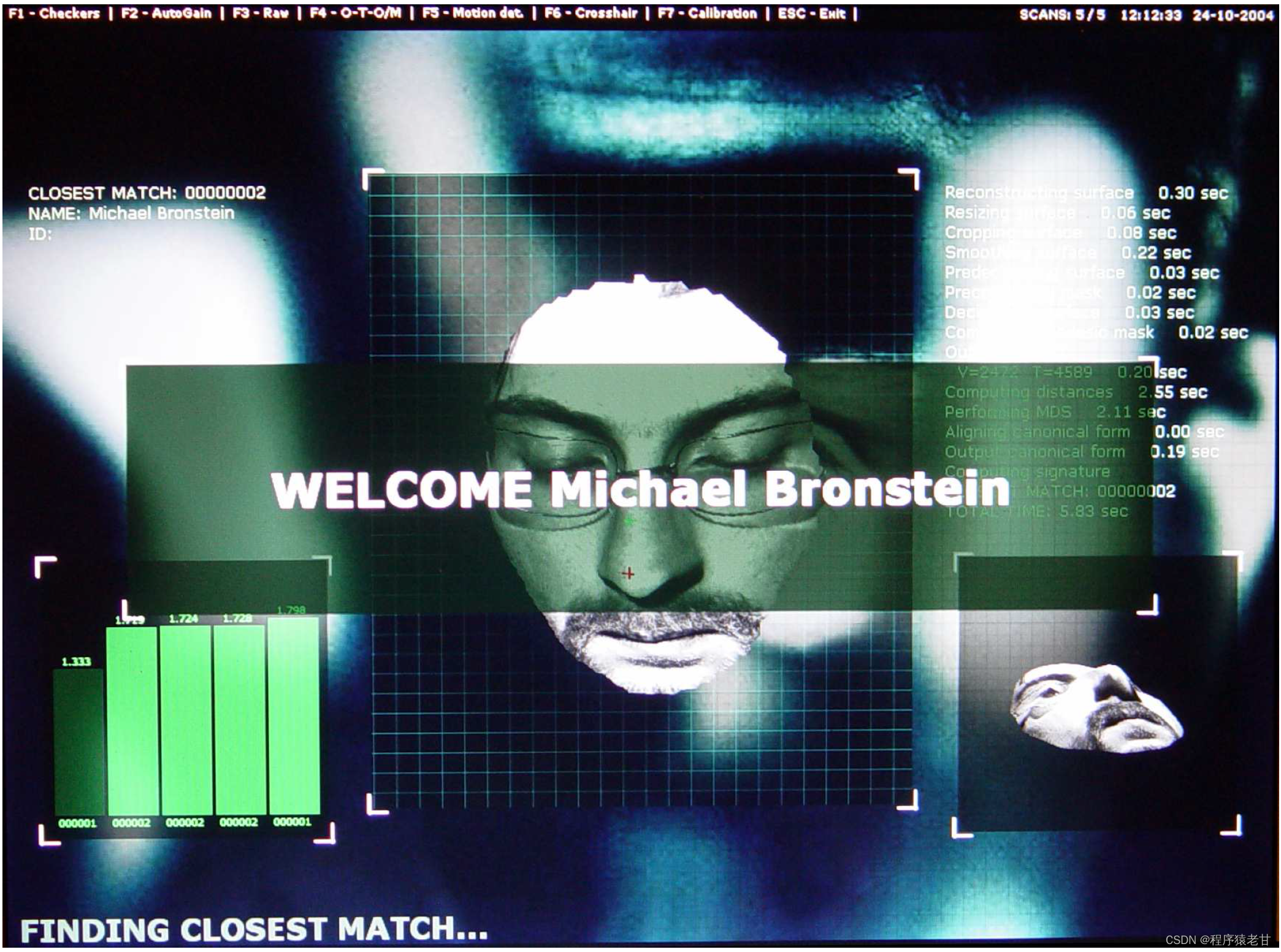
整个算法流程还是非常清晰的。但是求Δ需要的庞大计算量,限制了该算法的效率。
Reference
[1] Bronstein AM, Bronstein MM, Kimmel R. Three-dimensional face recognition[J]. International Journal of Computer Vision, 2005, 64: 5-30.
[2] Elad A, Kimmel R. Bending Invariant Representations for Surfaces[C]. Proceedings of the Conference on Computer Vision and Pattern Recognition, 2001, 2: 168-168.
[3] Bronstein AM, Bronstein MM, Kimmel R. Expression-invariant 3D face recognition[C]. International conference on Audio-and video-based biometric person authentication, 2003: 62-70.
[4] Young G, Householder A S. Discussion of a set of points in terms of their mutual distances[J]. Psychometrika, 1938, 3(1): 19-22.
相关文章:

Multidimensional Scaling(MDS多维缩放)算法及其应用
在这篇博客中,我将与大家分享在流形分析领域的一个非常重要的方法,即多维缩放MDS。整体来说,该方法提供了一种将内蕴距离映射到显性欧氏空间的计算,为非刚性形状分析提供了一种解决方案。当初就是因为读了Bronstein的相关工作【1】…...

单片机_RTOS_架构
一. RTOS的概念 // 经典单片机程序 void main() {while (1){喂一口饭();回一个信息();} } ------------------------------------------------------ // RTOS程序 喂饭() {while (1){喂一口饭();} }回信息() {while (1){回一个信息();} }void main() {create_task(喂饭);cr…...

Golang rsa 验证
一下代码用于rsa 签名的验签, 签名可以用其他语言产生。也可以用golang生成。 package mainimport ("crypto""crypto/rsa""crypto/sha256""crypto/x509""encoding/pem""errors""fmt" )fun…...

网络安全威胁——跨站脚本攻击
跨站脚本攻击 1. 定义2. 跨站脚本攻击如何工作3. 跨站脚本攻击类型4. 如何防止跨站脚本攻击 1. 定义 跨站脚本攻击(Cross-site Scripting,通常称为XSS),是一种典型的Web程序漏洞利用攻击,在线论坛、博客、留言板等共享…...
Java利用UDP实现简单的双人聊天
一、创建新项目 首先创建一个新的项目,并命名。 二、实现代码 import java.awt.*; import java.awt.event.*; import javax.swing.*; import java.net.*; import java.io.IOException; import java.lang.String; public class liaotian extends JFrame{ pri…...

HBase整合Phoenix
文章目录 一、简介1、Phoenix定义2、Phoenix架构 二、安装Phoenix1、安装 三、Phoenix操作1、Phoenix 数据映射2、Phoenix Shell操作3、Phoenix JDBC操作3.1 胖客户端3.2 瘦客户端 四、Phoenix二级索引1、为什么需要二级索引2、全局索引(global index)3、…...

C# 委托/事件/lambda
概念 委托 定义委托编译器会自动生成一个类派生自System.MulticastDelegate 这个类包含4个方法:一个构造器、Invoke、BeginInvoke、EndInvoke。 调用委托的时候实际上执行的是 Invoke方法。 MulticastDelegate类有三个重要字段: _targetÿ…...

13款趣味性不错(炫酷)的前端动画特效及源码(预览获取)分享(附源码)
文字激光打印特效 基于canvas实现的动画特效,你既可以设置初始的打印文字也可以在下方输入文字可实现激光字体打印,精简易用。 预览获取 核心代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8&q…...
C# 友元程序集
1.友元程序集 使用友元程序集可以将internal成员提供给其他的友元程序集访问。 程序集FriendTest1.dll [assembly:InternalsVisibleTo("FriendTest2")] namespace FriendTest1 {internal class Friend{string name;public string Name > name;public Friend(str…...
CRM系统的数据分析和报表功能对企业重要吗?
竞争日益激烈,企业需要更加高效地管理客户关系,以获取更多的商机。为此,许多企业选择使用CRM系统。在CRM中,数据分析功能扮演着重要的角色。下面就来详细说说,CRM系统数据分析与报表功能对企业来说重要吗? …...

【单体架构事务失效解决方式之___代理对象加锁】
单体架构__用户限买 一个id一单的多线程事务失效问题解决 背景介绍:有一种情况,我们在使用Synchronized的时候出现失效情况。 经过排查,是因为使用了this.当前对象,他现在使用的是目标对象加锁失效,使用代理对象加锁就…...

面试被问到 HTTP和HTTPS的区别有哪些?你该如何回答~
HTTP和HTTPS的区别有哪些,主要从以下几个方面来说: 1.安全性 HTTP和HTTPS是两种不同的协议,它们之间最主要的区别在于安全性。HTTP协议以明文方式发送内容,不提供任何方式的数据加密,容易被攻击者截取信息。 HTTPS则在…...
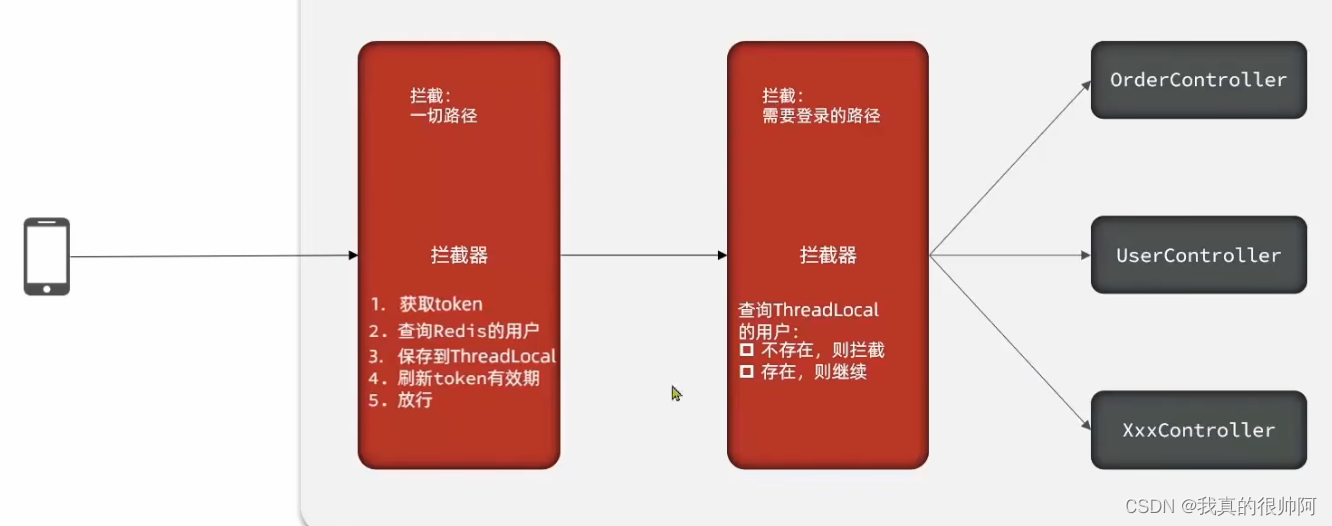
点评项目——短信登陆模块
2023.12.6 短信登陆如果基于session来实现,会存在session共享问题:多台Tomcat不能共享session存储空间,这会导致当请求切换到不同服务器时出现数据丢失的问题。 早期的解决办法是让session提供一个数据拷贝的功能,即让各个Tomcat的…...

2023亚太地区五岳杯量子计算挑战赛
计算电源网 (CPN)布局优化 1. 介绍 计算能力网络 (CPN)是一种基于业务需求分配和调度计算资源的新型信息基础设施,计算资源通常由终端用户、边缘服务器和云服务器组成。该网络旨在满足各种计算任务的需求。根据计算需求的空间分…...

Python 模块的使用方法
Python 模块是一种组织和封装代码的方式,允许你将相关的功能和变量放在一个单独的文件中,以便在其他程序中重复使用。在Python中,模块是一种可执行的Python脚本,其文件扩展名为 .py。这里,我将详细讲解Python模块的使用…...
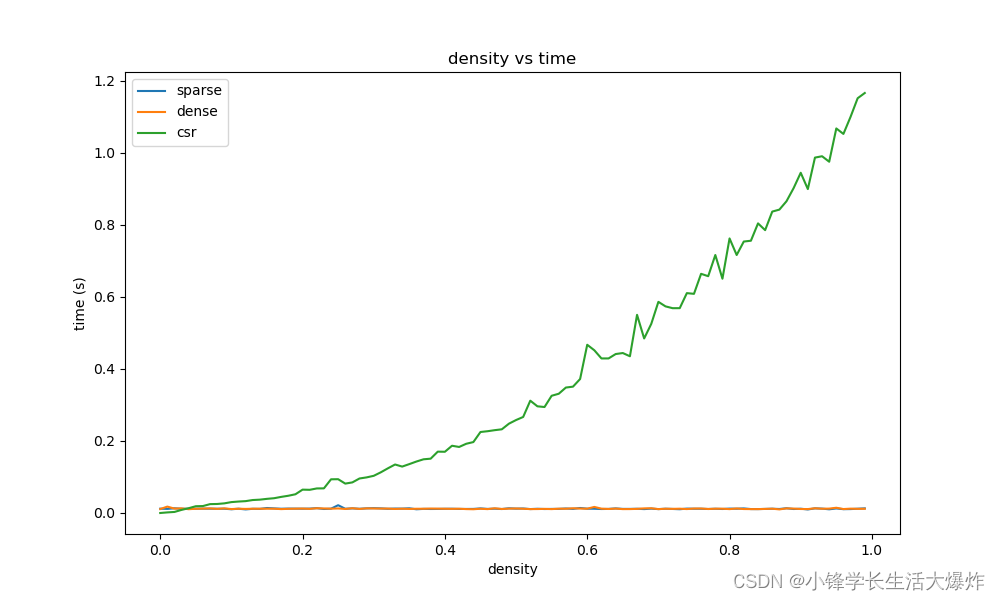
【知识】稀疏矩阵是否比密集矩阵更高效?
转载请注明出处:小锋学长生活大爆炸[xfxuezhang.cn] 问题提出 有些地方说,稀疏图比密集图的计算效率更高,真的吗? 原因猜想 这里的效率高,应该是有前提的:当使用稀疏矩阵的存储格式(如CSR)时,计…...

代码随想Day24 | 回溯法模板、77. 组合
理论基础 回溯法和递归不可分割,回溯法是一种穷举的方法,通常需要剪枝来降低复杂度。回溯法有一个选择并退回的过程,可以抽象为树结构,回溯法的模板如下: void backtracking(参数) {if (终止条件) {存放结果;return;}…...

搜索与回溯算法②
求0-9的数字可以组成的所有k 位数。 def backtrack(start, path, k, n, results):"""核心函数。:param start: 下一个添加的数字的起始位置:param path: 当前构建的路径,代表一个组合:param k: 组合中所需的数字个数:param n: 可选数字的最大值:par…...
Centos图形化界面封装OpenStack Ubuntu镜像
目录 背景 环境 搭建kvm环境 安装ubuntu虚机 虚机设置 系统安装 登录虚机 安装cloud-init 安装cloud-utils-growpart 关闭实例 删除细节信息 删除网卡细节 使虚机脱离libvirt纳管 结束与验证 压缩与转移 验证是否能够正常运行 背景 一般的镜像文件在上传OpenSt…...

使用Jmeter进行http接口测试怎么做?
前言: 本文主要针对http接口进行测试,使用Jmeter工具实现。 Jmter工具设计之初是用于做性能测试的,它在实现对各种接口的调用方面已经做的比较成熟,因此,本次直接使用Jmeter工具来完成对Http接口的测试。 一、开发接…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...
