[足式机器人]Part2 Dr. CAN学习笔记-Ch0-1矩阵的导数运算
本文仅供学习使用
本文参考:
B站:DR_CAN
Dr. CAN学习笔记-Ch0-1矩阵的导数运算
- 1. 标量向量方程对向量求导,分母布局,分子布局
- 1.1 标量方程对向量的导数
- 1.2 向量方程对向量的导数
- 2. 案例分析,线性回归
- 3. 矩阵求导的链式法则
1. 标量向量方程对向量求导,分母布局,分子布局
1.1 标量方程对向量的导数
- y y y 为 一元向量 或 二元向量
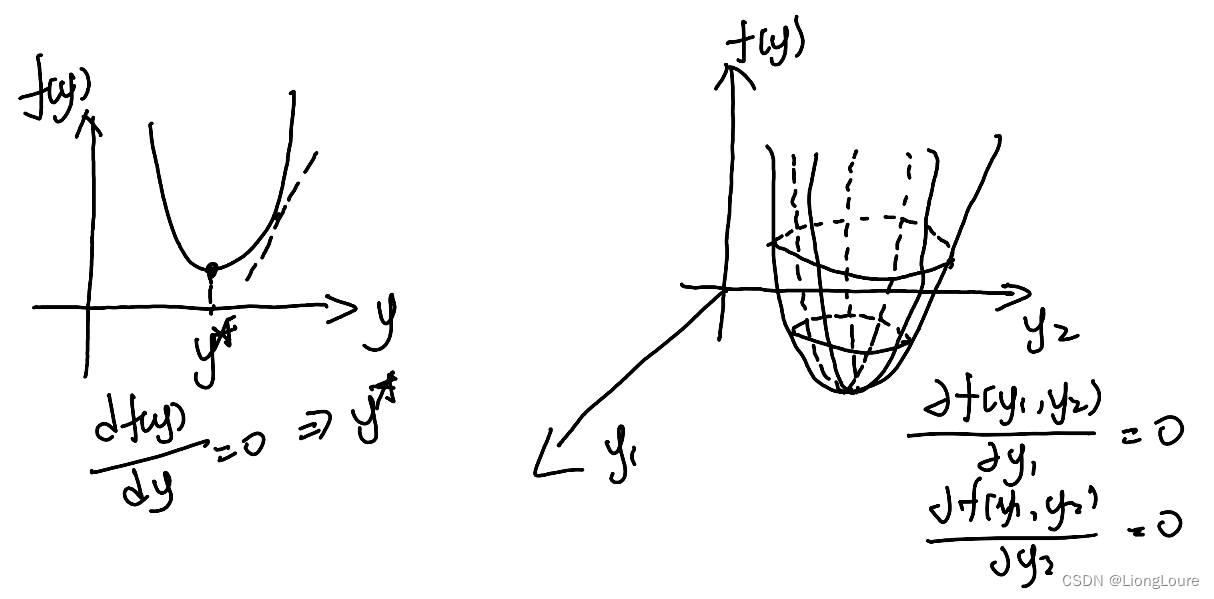
- y y y为多元向量
y ⃗ = [ y 1 , y 2 , ⋯ , y n ] ⇒ ∂ f ( y ⃗ ) ∂ y ⃗ \vec{y}=\left[ y_1,y_2,\cdots ,y_{\mathrm{n}} \right] \Rightarrow \frac{\partial f\left( \vec{y} \right)}{\partial \vec{y}} y=[y1,y2,⋯,yn]⇒∂y∂f(y)
其中: f ( y ⃗ ) f\left( \vec{y} \right) f(y) 为标量 1 × 1 1\times 1 1×1, y ⃗ \vec{y} y为向量 1 × n 1\times n 1×n
分母布局 Denominator Layout——行数与分母相同
∂ f ( y ⃗ ) ∂ y ⃗ = [ ∂ f ( y ⃗ ) ∂ y 1 ⋮ ∂ f ( y ⃗ ) ∂ y n ] n × 1 \frac{\partial f\left( \vec{y} \right)}{\partial \vec{y}}=\left[ \begin{array}{c} \frac{\partial f\left( \vec{y} \right)}{\partial y_1}\\ \vdots\\ \frac{\partial f\left( \vec{y} \right)}{\partial y_{\mathrm{n}}}\\ \end{array} \right] _{n\times 1} ∂y∂f(y)= ∂y1∂f(y)⋮∂yn∂f(y) n×1分子布局 Nunerator Layout——行数与分子相同
∂ f ( y ⃗ ) ∂ y ⃗ = [ ∂ f ( y ⃗ ) ∂ y 1 ⋯ ∂ f ( y ⃗ ) ∂ y n ] 1 × n \frac{\partial f\left( \vec{y} \right)}{\partial \vec{y}}=\left[ \begin{matrix} \frac{\partial f\left( \vec{y} \right)}{\partial y_1}& \cdots& \frac{\partial f\left( \vec{y} \right)}{\partial y_{\mathrm{n}}}\\ \end{matrix} \right] _{1\times n} ∂y∂f(y)=[∂y1∂f(y)⋯∂yn∂f(y)]1×n
1.2 向量方程对向量的导数
f ⃗ ( y ⃗ ) = [ f ⃗ 1 ( y ⃗ ) ⋮ f ⃗ n ( y ⃗ ) ] n × 1 , y ⃗ = [ y 1 ⋮ y m ] m × 1 \vec{f}\left( \vec{y} \right) =\left[ \begin{array}{c} \vec{f}_1\left( \vec{y} \right)\\ \vdots\\ \vec{f}_{\mathrm{n}}\left( \vec{y} \right)\\ \end{array} \right] _{n\times 1},\vec{y}=\left[ \begin{array}{c} y_1\\ \vdots\\ y_{\mathrm{m}}\\ \end{array} \right] _{\mathrm{m}\times 1} f(y)= f1(y)⋮fn(y) n×1,y= y1⋮ym m×1
∂ f ⃗ ( y ⃗ ) n × 1 ∂ y ⃗ m × 1 = [ ∂ f ⃗ ( y ⃗ ) ∂ y 1 ⋮ ∂ f ⃗ ( y ⃗ ) ∂ y m ] m × 1 = [ ∂ f 1 ( y ⃗ ) ∂ y 1 ⋯ ∂ f n ( y ⃗ ) ∂ y 1 ⋮ ⋱ ⋮ ∂ f 1 ( y ⃗ ) ∂ y m ⋯ ∂ f n ( y ⃗ ) ∂ y m ] m × n \frac{\partial \vec{f}\left( \vec{y} \right) _{n\times 1}}{\partial \vec{y}_{\mathrm{m}\times 1}}=\left[ \begin{array}{c} \frac{\partial \vec{f}\left( \vec{y} \right)}{\partial y_1}\\ \vdots\\ \frac{\partial \vec{f}\left( \vec{y} \right)}{\partial y_{\mathrm{m}}}\\ \end{array} \right] _{\mathrm{m}\times 1}=\left[ \begin{matrix} \frac{\partial f_1\left( \vec{y} \right)}{\partial y_1}& \cdots& \frac{\partial f_{\mathrm{n}}\left( \vec{y} \right)}{\partial y_1}\\ \vdots& \ddots& \vdots\\ \frac{\partial f_1\left( \vec{y} \right)}{\partial y_{\mathrm{m}}}& \cdots& \frac{\partial f_{\mathrm{n}}\left( \vec{y} \right)}{\partial y_{\mathrm{m}}}\\ \end{matrix} \right] _{\mathrm{m}\times \mathrm{n}} ∂ym×1∂f(y)n×1= ∂y1∂f(y)⋮∂ym∂f(y) m×1= ∂y1∂f1(y)⋮∂ym∂f1(y)⋯⋱⋯∂y1∂fn(y)⋮∂ym∂fn(y) m×n, 为分母布局
若: y ⃗ = [ y 1 ⋮ y m ] m × 1 , A = [ a 11 ⋯ a 1 n ⋮ ⋱ ⋮ a m 1 ⋯ a m n ] \vec{y}=\left[ \begin{array}{c} y_1\\ \vdots\\ y_{\mathrm{m}}\\ \end{array} \right] _{\mathrm{m}\times 1}, A=\left[ \begin{matrix} a_{11}& \cdots& a_{1\mathrm{n}}\\ \vdots& \ddots& \vdots\\ a_{\mathrm{m}1}& \cdots& a_{\mathrm{mn}}\\ \end{matrix} \right] y= y1⋮ym m×1,A= a11⋮am1⋯⋱⋯a1n⋮amn , 则有:
- ∂ A y ⃗ ∂ y ⃗ = A T \frac{\partial A\vec{y}}{\partial \vec{y}}=A^{\mathrm{T}} ∂y∂Ay=AT(分母布局)
- ∂ y ⃗ T A y ⃗ ∂ y ⃗ = A y ⃗ + A T y ⃗ \frac{\partial \vec{y}^{\mathrm{T}}A\vec{y}}{\partial \vec{y}}=A\vec{y}+A^{\mathrm{T}}\vec{y} ∂y∂yTAy=Ay+ATy, 当 A = A T A=A^{\mathrm{T}} A=AT时, ∂ y ⃗ T A y ⃗ ∂ y ⃗ = 2 A y ⃗ \frac{\partial \vec{y}^{\mathrm{T}}A\vec{y}}{\partial \vec{y}}=2A\vec{y} ∂y∂yTAy=2Ay
若为分子布局,则有: ∂ A y ⃗ ∂ y ⃗ = A \frac{\partial A\vec{y}}{\partial \vec{y}}=A ∂y∂Ay=A
2. 案例分析,线性回归
- ∂ A y ⃗ ∂ y ⃗ = A T \frac{\partial A\vec{y}}{\partial \vec{y}}=A^{\mathrm{T}} ∂y∂Ay=AT(分母布局)
- ∂ y ⃗ T A y ⃗ ∂ y ⃗ = A y ⃗ + A T y ⃗ \frac{\partial \vec{y}^{\mathrm{T}}A\vec{y}}{\partial \vec{y}}=A\vec{y}+A^{\mathrm{T}}\vec{y} ∂y∂yTAy=Ay+ATy, 当 A = A T A=A^{\mathrm{T}} A=AT时, ∂ y ⃗ T A y ⃗ ∂ y ⃗ = 2 A y ⃗ \frac{\partial \vec{y}^{\mathrm{T}}A\vec{y}}{\partial \vec{y}}=2A\vec{y} ∂y∂yTAy=2Ay
Linear Regression 线性回归
z ^ = y 1 + y 2 x ⇒ J = ∑ i = 1 n [ z i − ( y 1 + y 2 x i ) ] 2 \hat{z}=y_1+y_2x\Rightarrow J=\sum_{i=1}^n{\left[ z_i-\left( y_1+y_2x_i \right) \right] ^2} z^=y1+y2x⇒J=i=1∑n[zi−(y1+y2xi)]2
找到 y 1 , y 2 y_1,y_2 y1,y2 使得 J J J最小
z ⃗ = [ z 1 ⋮ z n ] , [ x ⃗ ] = [ 1 x 1 ⋮ ⋮ 1 x n ] , y ⃗ = [ y 1 y 2 ] ⇒ z ⃗ ^ = [ x ⃗ ] y ⃗ = [ y 1 + y 2 x 1 ⋮ y 1 + y 2 x n ] \vec{z}=\left[ \begin{array}{c} z_1\\ \vdots\\ z_{\mathrm{n}}\\ \end{array} \right] ,\left[ \vec{x} \right] =\left[ \begin{array}{l} 1& x_1\\ \vdots& \vdots\\ 1& x_{\mathrm{n}}\\ \end{array} \right] ,\vec{y}=\left[ \begin{array}{c} y_1\\ y_2\\ \end{array} \right] \Rightarrow \hat{\vec{z}}=\left[ \vec{x} \right] \vec{y}=\left[ \begin{array}{c} y_1+y_2x_1\\ \vdots\\ y_1+y_2x_{\mathrm{n}}\\ \end{array} \right] z= z1⋮zn ,[x]= 1⋮1x1⋮xn ,y=[y1y2]⇒z^=[x]y= y1+y2x1⋮y1+y2xn
J = [ z ⃗ − z ⃗ ^ ] T [ z ⃗ − z ⃗ ^ ] = [ z ⃗ − [ x ⃗ ] y ⃗ ] T [ z ⃗ − [ x ⃗ ] y ⃗ ] = z ⃗ z ⃗ T − z ⃗ T [ x ⃗ ] y ⃗ − y ⃗ T [ x ⃗ ] T z ⃗ + y ⃗ T [ x ⃗ ] T [ x ⃗ ] y ⃗ J=\left[ \vec{z}-\hat{\vec{z}} \right] ^{\mathrm{T}}\left[ \vec{z}-\hat{\vec{z}} \right] =\left[ \vec{z}-\left[ \vec{x} \right] \vec{y} \right] ^{\mathrm{T}}\left[ \vec{z}-\left[ \vec{x} \right] \vec{y} \right] =\vec{z}\vec{z}^{\mathrm{T}}-\vec{z}^{\mathrm{T}}\left[ \vec{x} \right] \vec{y}-\vec{y}^{\mathrm{T}}\left[ \vec{x} \right] ^{\mathrm{T}}\vec{z}+\vec{y}^{\mathrm{T}}\left[ \vec{x} \right] ^{\mathrm{T}}\left[ \vec{x} \right] \vec{y} J=[z−z^]T[z−z^]=[z−[x]y]T[z−[x]y]=zzT−zT[x]y−yT[x]Tz+yT[x]T[x]y
其中: ( z ⃗ T [ x ⃗ ] y ⃗ ) T = y ⃗ T [ x ⃗ ] T z ⃗ \left( \vec{z}^{\mathrm{T}}\left[ \vec{x} \right] \vec{y} \right) ^{\mathrm{T}}=\vec{y}^{\mathrm{T}}\left[ \vec{x} \right] ^{\mathrm{T}}\vec{z} (zT[x]y)T=yT[x]Tz, 则有:
J = z ⃗ z ⃗ T − 2 z ⃗ T [ x ⃗ ] y ⃗ + y ⃗ T [ x ⃗ ] T [ x ⃗ ] y ⃗ J=\vec{z}\vec{z}^{\mathrm{T}}-2\vec{z}^{\mathrm{T}}\left[ \vec{x} \right] \vec{y}+\vec{y}^{\mathrm{T}}\left[ \vec{x} \right] ^{\mathrm{T}}\left[ \vec{x} \right] \vec{y} J=zzT−2zT[x]y+yT[x]T[x]y
进而:
∂ J ∂ y ⃗ = 0 − 2 ( z ⃗ T [ x ⃗ ] ) T + 2 [ x ⃗ ] T [ x ⃗ ] y ⃗ = ∇ y ⃗ ⟹ ∂ J ∂ y ⃗ ∗ = 0 , y ⃗ ∗ = ( [ x ⃗ ] T [ x ⃗ ] ) − 1 [ x ⃗ ] T z ⃗ \frac{\partial J}{\partial \vec{y}}=0-2\left( \vec{z}^{\mathrm{T}}\left[ \vec{x} \right] \right) ^{\mathrm{T}}+2\left[ \vec{x} \right] ^{\mathrm{T}}\left[ \vec{x} \right] \vec{y}=\nabla \vec{y}\Longrightarrow \frac{\partial J}{\partial \vec{y}^*}=0,\vec{y}^*=\left( \left[ \vec{x} \right] ^{\mathrm{T}}\left[ \vec{x} \right] \right) ^{-1}\left[ \vec{x} \right] ^{\mathrm{T}}\vec{z} ∂y∂J=0−2(zT[x])T+2[x]T[x]y=∇y⟹∂y∗∂J=0,y∗=([x]T[x])−1[x]Tz
其中: ( [ x ⃗ ] T [ x ⃗ ] ) − 1 \left( \left[ \vec{x} \right] ^{\mathrm{T}}\left[ \vec{x} \right] \right) ^{-1} ([x]T[x])−1不一定有解,则 y ⃗ ∗ \vec{y}^* y∗无法得到解析解——定义初始 y ⃗ ∗ \vec{y}^* y∗, y ⃗ ∗ = y ⃗ ∗ − α ∇ , α = [ α 1 0 0 α 2 ] \vec{y}^*=\vec{y}^*-\alpha \nabla ,\alpha =\left[ \begin{matrix} \alpha _1& 0\\ 0& \alpha _2\\ \end{matrix} \right] y∗=y∗−α∇,α=[α100α2]
其中: α \alpha α称为学习率,对 x x x而言则需进行归一化
3. 矩阵求导的链式法则
标量函数: J = f ( y ( u ) ) , ∂ J ∂ u = ∂ J ∂ y ∂ y ∂ u J=f\left( y\left( u \right) \right) ,\frac{\partial J}{\partial u}=\frac{\partial J}{\partial y}\frac{\partial y}{\partial u} J=f(y(u)),∂u∂J=∂y∂J∂u∂y
标量对向量求导: J = f ( y ⃗ ( u ⃗ ) ) , y ⃗ = [ y 1 ( u ⃗ ) ⋮ y m ( u ⃗ ) ] m × 1 , u ⃗ = [ u ⃗ 1 ⋮ u ⃗ n ] n × 1 J=f\left( \vec{y}\left( \vec{u} \right) \right) ,\vec{y}=\left[ \begin{array}{c} y_1\left( \vec{u} \right)\\ \vdots\\ y_{\mathrm{m}}\left( \vec{u} \right)\\ \end{array} \right] _{m\times 1},\vec{u}=\left[ \begin{array}{c} \vec{u}_1\\ \vdots\\ \vec{u}_{\mathrm{n}}\\ \end{array} \right] _{\mathrm{n}\times 1} J=f(y(u)),y= y1(u)⋮ym(u) m×1,u= u1⋮un n×1
分析: ∂ J 1 × 1 ∂ u n × 1 n × 1 = ∂ J ∂ y m × 1 m × 1 ∂ y m × 1 ∂ u n × 1 n × m \frac{\partial J_{1\times 1}}{\partial u_{\mathrm{n}\times 1}}_{\mathrm{n}\times 1}=\frac{\partial J}{\partial y_{m\times 1}}_{m\times 1}\frac{\partial y_{m\times 1}}{\partial u_{\mathrm{n}\times 1}}_{\mathrm{n}\times \mathrm{m}} ∂un×1∂J1×1n×1=∂ym×1∂Jm×1∂un×1∂ym×1n×m 无法相乘
y ⃗ = [ y 1 ( u ⃗ ) y 2 ( u ⃗ ) ] 2 × 1 , u ⃗ = [ u ⃗ 1 u ⃗ 2 u ⃗ 3 ] 3 × 1 \vec{y}=\left[ \begin{array}{c} y_1\left( \vec{u} \right)\\ y_2\left( \vec{u} \right)\\ \end{array} \right] _{2\times 1},\vec{u}=\left[ \begin{array}{c} \vec{u}_1\\ \vec{u}_2\\ \vec{u}_3\\ \end{array} \right] _{3\times 1} y=[y1(u)y2(u)]2×1,u= u1u2u3 3×1
J = f ( y ⃗ ( u ⃗ ) ) , ∂ J ∂ u ⃗ = [ ∂ J ∂ u ⃗ 1 ∂ J ∂ u ⃗ 2 ∂ J ∂ u ⃗ 3 ] 3 × 1 ⟹ ∂ J ∂ u ⃗ 1 = ∂ J ∂ y 1 ∂ y 1 ( u ⃗ ) ∂ u ⃗ 1 + ∂ J ∂ y 2 ∂ y 2 ( u ⃗ ) ∂ u ⃗ 1 ∂ J ∂ u ⃗ 2 = ∂ J ∂ y 1 ∂ y 1 ( u ⃗ ) ∂ u ⃗ 2 + ∂ J ∂ y 2 ∂ y 2 ( u ⃗ ) ∂ u ⃗ 2 ∂ J ∂ u ⃗ 3 = ∂ J ∂ y 1 ∂ y 1 ( u ⃗ ) ∂ u ⃗ 3 + ∂ J ∂ y 2 ∂ y 2 ( u ⃗ ) ∂ u ⃗ 3 ⟹ ∂ J ∂ u ⃗ = [ ∂ y 1 ( u ⃗ ) ∂ u ⃗ 1 ∂ y 2 ( u ⃗ ) ∂ u ⃗ 1 ∂ y 1 ( u ⃗ ) ∂ u ⃗ 2 ∂ y 2 ( u ⃗ ) ∂ u ⃗ 2 ∂ y 1 ( u ⃗ ) ∂ u ⃗ 3 ∂ y 2 ( u ⃗ ) ∂ u ⃗ 3 ] 3 × 2 [ ∂ J ∂ y 1 ∂ J ∂ y 2 ] 2 × 2 = ∂ y ⃗ ( u ⃗ ) ∂ u ⃗ ∂ J ∂ y ⃗ J=f\left( \vec{y}\left( \vec{u} \right) \right) ,\frac{\partial J}{\partial \vec{u}}=\left[ \begin{array}{c} \frac{\partial J}{\partial \vec{u}_1}\\ \frac{\partial J}{\partial \vec{u}_2}\\ \frac{\partial J}{\partial \vec{u}_3}\\ \end{array} \right] _{3\times 1}\Longrightarrow \begin{array}{c} \frac{\partial J}{\partial \vec{u}_1}=\frac{\partial J}{\partial y_1}\frac{\partial y_1\left( \vec{u} \right)}{\partial \vec{u}_1}+\frac{\partial J}{\partial y_2}\frac{\partial y_2\left( \vec{u} \right)}{\partial \vec{u}_1}\\ \frac{\partial J}{\partial \vec{u}_2}=\frac{\partial J}{\partial y_1}\frac{\partial y_1\left( \vec{u} \right)}{\partial \vec{u}_2}+\frac{\partial J}{\partial y_2}\frac{\partial y_2\left( \vec{u} \right)}{\partial \vec{u}_2}\\ \frac{\partial J}{\partial \vec{u}_3}=\frac{\partial J}{\partial y_1}\frac{\partial y_1\left( \vec{u} \right)}{\partial \vec{u}_3}+\frac{\partial J}{\partial y_2}\frac{\partial y_2\left( \vec{u} \right)}{\partial \vec{u}_3}\\ \end{array} \\ \Longrightarrow \frac{\partial J}{\partial \vec{u}}=\left[ \begin{array}{l} \frac{\partial y_1\left( \vec{u} \right)}{\partial \vec{u}_1}& \frac{\partial y_2\left( \vec{u} \right)}{\partial \vec{u}_1}\\ \frac{\partial y_1\left( \vec{u} \right)}{\partial \vec{u}_2}& \frac{\partial y_2\left( \vec{u} \right)}{\partial \vec{u}_2}\\ \frac{\partial y_1\left( \vec{u} \right)}{\partial \vec{u}_3}& \frac{\partial y_2\left( \vec{u} \right)}{\partial \vec{u}_3}\\ \end{array} \right] _{3\times 2}\left[ \begin{array}{c} \frac{\partial J}{\partial y_1}\\ \frac{\partial J}{\partial y_2}\\ \end{array} \right] _{2\times 2}=\frac{\partial \vec{y}\left( \vec{u} \right)}{\partial \vec{u}}\frac{\partial J}{\partial \vec{y}} J=f(y(u)),∂u∂J= ∂u1∂J∂u2∂J∂u3∂J 3×1⟹∂u1∂J=∂y1∂J∂u1∂y1(u)+∂y2∂J∂u1∂y2(u)∂u2∂J=∂y1∂J∂u2∂y1(u)+∂y2∂J∂u2∂y2(u)∂u3∂J=∂y1∂J∂u3∂y1(u)+∂y2∂J∂u3∂y2(u)⟹∂u∂J= ∂u1∂y1(u)∂u2∂y1(u)∂u3∂y1(u)∂u1∂y2(u)∂u2∂y2(u)∂u3∂y2(u) 3×2[∂y1∂J∂y2∂J]2×2=∂u∂y(u)∂y∂J
∂ J ∂ u ⃗ = ∂ y ⃗ ( u ⃗ ) ∂ u ⃗ ∂ J ∂ y ⃗ \frac{\partial J}{\partial \vec{u}}=\frac{\partial \vec{y}\left( \vec{u} \right)}{\partial \vec{u}}\frac{\partial J}{\partial \vec{y}} ∂u∂J=∂u∂y(u)∂y∂J
eg:
x ⃗ [ k + 1 ] = A x ⃗ [ k ] + B u ⃗ [ k ] , J = x ⃗ T [ k + 1 ] x ⃗ [ k + 1 ] \vec{x}\left[ k+1 \right] =A\vec{x}\left[ k \right] +B\vec{u}\left[ k \right] ,J=\vec{x}^{\mathrm{T}}\left[ k+1 \right] \vec{x}\left[ k+1 \right] x[k+1]=Ax[k]+Bu[k],J=xT[k+1]x[k+1]
∂ J ∂ u ⃗ = ∂ x ⃗ [ k + 1 ] ∂ u ⃗ ∂ J ∂ x ⃗ [ k + 1 ] = B T ⋅ 2 x ⃗ [ k + 1 ] = 2 B T x ⃗ [ k + 1 ] \frac{\partial J}{\partial \vec{u}}=\frac{\partial \vec{x}\left[ k+1 \right]}{\partial \vec{u}}\frac{\partial J}{\partial \vec{x}\left[ k+1 \right]}=B^{\mathrm{T}}\cdot 2\vec{x}\left[ k+1 \right] =2B^{\mathrm{T}}\vec{x}\left[ k+1 \right] ∂u∂J=∂u∂x[k+1]∂x[k+1]∂J=BT⋅2x[k+1]=2BTx[k+1]
相关文章:

[足式机器人]Part2 Dr. CAN学习笔记-Ch0-1矩阵的导数运算
本文仅供学习使用 本文参考: B站:DR_CAN Dr. CAN学习笔记-Ch0-1矩阵的导数运算 1. 标量向量方程对向量求导,分母布局,分子布局1.1 标量方程对向量的导数1.2 向量方程对向量的导数 2. 案例分析,线性回归3. 矩阵求导的链…...
如何让软文更具画面感,媒介盒子分享
写软文这种带有销售性质的文案时,总说要有画面感,要有想象空间。只有针对目标用户的感受的设计,要了解用户想的是什么,要用可视化的描述来影响用户的感受,今天媒介盒子就和大家分享:如何让软文更具画面感。…...

Hadoop学习笔记(HDP)-Part.19 安装Kafka
目录 Part.01 关于HDP Part.02 核心组件原理 Part.03 资源规划 Part.04 基础环境配置 Part.05 Yum源配置 Part.06 安装OracleJDK Part.07 安装MySQL Part.08 部署Ambari集群 Part.09 安装OpenLDAP Part.10 创建集群 Part.11 安装Kerberos Part.12 安装HDFS Part.13 安装Ranger …...

Arrays类练习 - Java
案例:自定义Book类,里面包含name和price,按price排序(从大到小)。要求使用两种方式排序,有一个 Book[] books 4本书对象。 使用前面学习过的传递实现Comparator接口匿名内部类,也称为定制排序。可以按照price (1)从大到…...

Java多线程:代码不只是在‘Hello World‘
Java线程好书推荐 概述01 多线程对于Java的意义02 为什么Java工程师必须掌握多线程03 Java多线程使用方式04 如何学好Java多线程写在末尾: 主页传送门:📀 传送 概述 摘要:互联网的每一个角落,无论是大型电商平台的秒杀…...

使用PCSS实现的实时阴影效果
PCSS的技术可以使得阴影呈现出近硬远软的效果,并且能够实时实现。 其核心理念是通过模拟光源的面积来产生更自然、更柔和的阴影边缘。 具体步骤: 1、生成shadowmap 2、在进行阴影的比较时候进行平均,并非之前的shadow map 或者之后完全的阴影…...
用于缓存一些固定名称的小组件
项目中,用于缓存姓名、地名、单位名称等一些较固定名称的id-name小组件。用于减少一些表的关连操作和冗余字段。优化代码结构。扩展也方便,写不同的枚举就行了。 具体用法: {NameCacheUser.USER.getName(userId);NameCacheUser.ACCOUNT.getN…...

Python 读取电子发票PDF 转成Excel
Python 读取电子发票PDF 转成Excel 目录 0.前提 1.python相关的处理PDF的库 2.实际好用的 3.实际代码 4.思考 0.前提 只识别普通电子发票PDF,提取其中某些关键内容到excel中。 1.python相关的处理PDF的库 如下4个库是经常更新维护的! pyP…...
我的项目问题
1.一点缩放和旋转就消失,需要再次平移才出现 解决方案:在显示当前图形时,显示已有图形。 2.每次点击平移,图形移动到上次点击的位置。 ho_RegionUnion.Dispose(); ho_RegionUnion ExpTmpOutVar_0;这两段代码放到显示之后的&am…...
【c】杨辉三角
下面介绍两种方法 1.利用上面性质的第五条,我们可以求各行各列的组合数 2.利用上面性质的第7条,我们可以用数组完成 下面附上代码 1. #include<stdio.h> void fact(int n ,int m )//求组合数 {long long int sum11;long long int sum21;int a…...

算法刷题之数组篇
题目一:两数之和 给出一个整型数组 numbers 和一个目标值 target,请在数组中找出两个加起来等于目标值的数的下标,返回的下标按升序排列。 (注:返回的数组下标从1开始算起,保证target一定可以由数组里面2…...
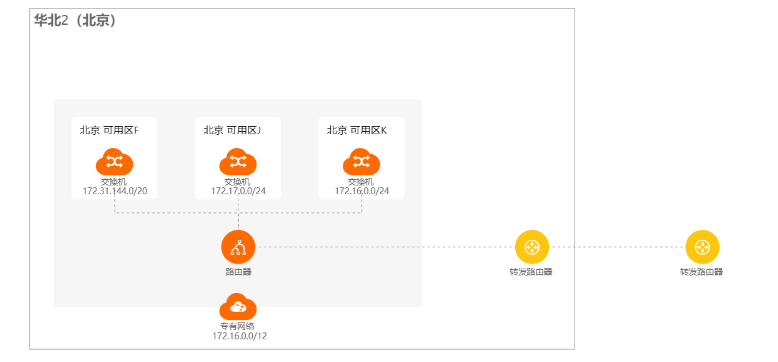
TR转发路由器测评—云企业网实现跨地域跨VPC的网络互通测评实战【阿里云产品测评】
文章目录 一.转发路由器 Transit Router 测评1.1 准备阶段1.2 本文测评收获1.3 什么是云企业网实例、转发路由器实例和云数据传输服务 二.使用云企业网实现跨地域跨VPC的网络互通2.2 **测试连通性**2.3 网络拓扑如下: 心得:总结: 声明&#x…...
1.1美术理论基础
一、光影 物体呈现在人们眼前的时候,不同的受光面其明暗变化以及物体的影子。 1.什么是黑白灰 在美术中黑白灰指亮面、灰面、暗面,属于素描的三大面,主要体验一个物体的整体寿光过程。普遍存在于各种艺术和设计领域。黑白灰作品的出现&#x…...

【Java 基础】21 多线程同步与锁
文章目录 1.存在的问题2.使用同步解决问题1) synchronized2) volatile3) 锁 总结 用多线程过程中,有可能出现 多个线程同时处理(获取或修改等)同一个数据,这个时候就 会发生数据不同步的问题, 因此出现了同步和锁来…...

Python语言基础知识(一)
文章目录 1、Python内置对象介绍2、标识符与变量3、数据类型—数字4、数据类型—字符串与字节串5、数据类型—列表、元组、字典、集合6、运算符和表达式7、运算符和表达式—算术运算符8、运算符和表达式—关系运算符9.1、运算符和表达式— 成员测试运算符in9.2、运算符和表达式…...
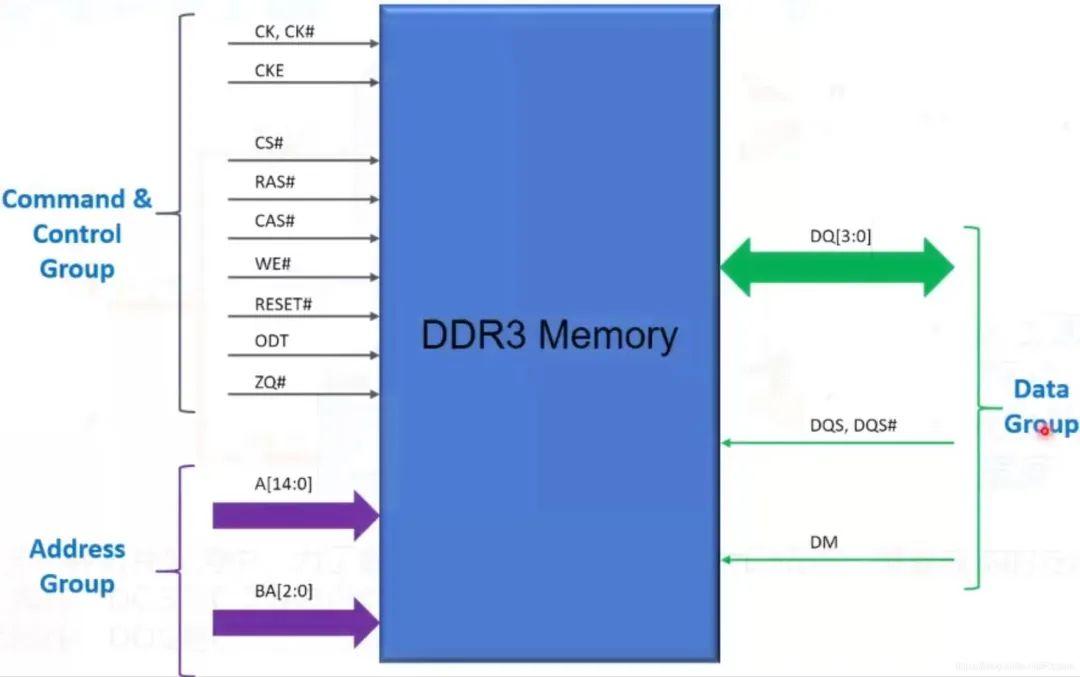
Xilinx FPGA平台DDR3设计详解(三):DDR3 介绍
本文介绍一下常用的存储芯片DDR3,包括DDR3的芯片型号识别、DDR3芯片命名、DDR3的基本结构等知识,为后续掌握FPGA DDR3的读写控制打下坚实基础。 一、DDR3芯片型号 电路板上的镁光DDR3芯片上没有具体的型号名。 如果想知道具体的DDR3芯片型号&#…...

字典的遍历
字典不是有序的集合,就不能通过index来遍历了,那如何遍历字典呢? 方法一:直接用字典 for key in a_dict: print a_dict[key] 通过这样的结构可以的。 d {"liming" : 98, "wangli":95, "mali":90, "liping&q…...
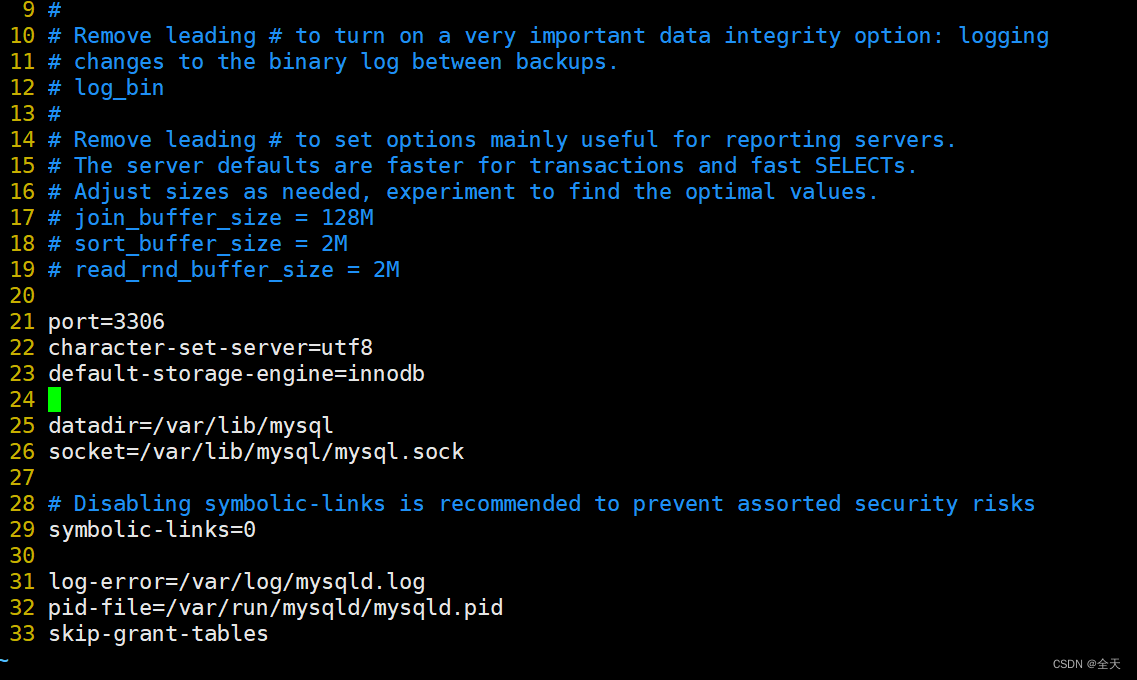
Linux环境下的MySQL安装
文章目录 前提说明1.卸载内置环境2.检查系统安装包3.卸载这些默认安装包4.获取MySQL官方yum源5.安装MySQLyum源,对比前后yum源6.查看yum源是否生效7.安装MySQL服务8.查看相对应的配置文件9.启动服务10.查看启动服务11.登录方法一12.登录方法二13.登录方法三14.设置开…...

梦想与魔法:编程之路的挑战与荣耀
在年少轻狂的岁月里,我们都有过一些不切实际的梦想,渴望成为某种神奇的存在。我的梦想是成为一名神奇的码农,用键盘编织魔法,创造出炫酷的虚拟世界。然而,现实是残酷的,当我刚入门计算机领域时,…...

qt 5.15.2 主窗体菜单工具栏树控件功能
qt 5.15.2 主窗体菜单工具栏树控件功能 显示主窗体效果: mainwindow.h文件内容: #ifndef MAINWINDOW_H #define MAINWINDOW_H#include <QMainWindow> #include <QFileDialog> #include <QString> #include <QMessageBox>#inc…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...
