【论文合集】在非欧空间中的图嵌入方法(Graph Embedding in Non-Euclidean Space)
文章目录
- 1. Hyperbolic Models
- 1.1 Hyperbolic Graph Attention Network
- 1.2 Poincaré Embeddings for Learning Hierarchical Representations.
- 1.3 Learning Continuous Hierarchies in the Lorentz Model of Hyperbolic Geometry
- 1.4 Hyperbolic Graph Convolutional Neural Networks
- 1.5 Lorentzian Graph Convolutional Networks
- 2. Spherical models
- 2.1 Geometry Interaction Knowledge Graph Embeddings
- 2.2 Hyperbolic Geometry of Complex Networks
- 2.3 DeepSphere: A graph-based spherical CNN
- 3. Gaussian Embedding Models
- 3.1 Deep Variational Network Embedding in Wasserstein Space
- 3.2 Multilabel Classification on Heterogeneous Graphs with Gaussian Embeddings
- 3.3 Deep Gaussian Embedding of Graphs: Unsupervised Inductive Learning via Ranking
- 3.4 Learning to Represent Knowledge Graphs with Gaussian Embedding
大多数现有的图嵌入模型旨在学习欧几里得空间中的嵌入,这可能不能提供良好的几何表示和度量值。最近的研究表明,非欧几里得空间更适合用于表示复杂的图结构。非欧几里得模型可以分为双曲模型、球形模型和高斯模型。双曲空间和球面空间是两种非欧几里得几何,它们可以代表不同的图结构。双曲空间更适合表示遵循幂律的层次图结构,而球面空间的幂次空间更适合表示大圆图结构。
分为 Hyperbolic Models,Spherical models 和 Gaussian models三类
1. Hyperbolic Models
1.1 Hyperbolic Graph Attention Network
**摘要:**图神经网络(GNN)在处理结构化图方面表现出优越的性能,近期引起了相当多的研究关注。大多数现有的GNN都是在欧几里得空间中设计的;然而,现实世界中的空间结构化数据可以是非欧几里得表面(例如,双曲空间)。例如,生物学家可能会检查蛋白质表面的几何形状,以确定其与其他生物分子的相互作用,用于药物发现。尽管有越来越多的研究将GNN推广到非欧几里得表面,但这些领域的研究工作仍然很有限。在本文中,我们利用图注意力网络来学习双曲空间中图的稳健节点表示。由于陀螺矢量空间框架为双曲几何提供了一种优雅的代数形式,我们利用这个框架来学习双曲空间中的图表示。具体而言,我们首先使用框架中定义的操作来转换图中的特征;我们利用双曲空间乘积中的接近性来模拟非欧几里得设置中的多头注意机制;随后,我们进一步设计了一种并行策略,使用对数和指数映射来提高我们提出的模型的效率。全面的实验结果表明,与最先进的方法相比,所提出的模型具有显著的有效性。

- 把图注意力网络从欧式空间迁到双曲空间更有利于建模层次结构
Y. Zhang, X. Wang, C. Shi, X. Jiang and Y. Ye, “Hyperbolic Graph Attention Network,” in IEEE Transactions on Big Data, vol. 8, no. 6, pp. 1690-1701, 1 Dec. 2022, doi: 10.1109/TBDATA.2021.3081431.
1.2 Poincaré Embeddings for Learning Hierarchical Representations.
**摘要:**表征学习已经成为从符号数据(如文本和图形)中学习的一种宝贵方法。然而,最先进的嵌入方法通常没有考虑到许多复杂符号数据集特有的潜在层次结构。在这项工作中,我们引入了一种新的方法,通过将符号数据嵌入到双曲空间中(更准确地说是嵌入到n维的庞加莱球),来学习符号数据的层次化表示。由于底层的双曲几何,这使我们能够通过同时捕捉层次结构和相似性来学习符号数据的简洁表示。我们提出了一种基于黎曼优化的高效算法来学习嵌入,并通过实验证明,在具有潜在层次结构的数据中,庞加莱嵌入在表示容量和泛化能力方面都能显著优于欧几里得嵌入。

- 最早使用庞加莱球空间来建模WordNet的论文
Maximilian Nickel and Douwe Kiela. 2017. Poincaré embeddings for learning hierarchical representations. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS’17). Curran Associates Inc., Red Hook, NY, USA, 6341–6350.
1.3 Learning Continuous Hierarchies in the Lorentz Model of Hyperbolic Geometry
**摘要:**我们关注从大规模非结构化相似性分数中发现层次关系。为此,我们研究了双曲空间的不同模型,并发现在洛伦兹模型中学习嵌入比在庞加莱球模型中更为高效。我们展示了所提出的方法使我们能够学习大型分类体系的高质量嵌入,相对于庞加莱嵌入,特别是在低维度下,取得了改进。最后,我们将我们的模型应用于发现两个现实世界数据集中的层次结构:我们展示了在双曲空间中嵌入可以揭示公司组织结构的重要方面,并揭示了语言家族之间的历史关系。
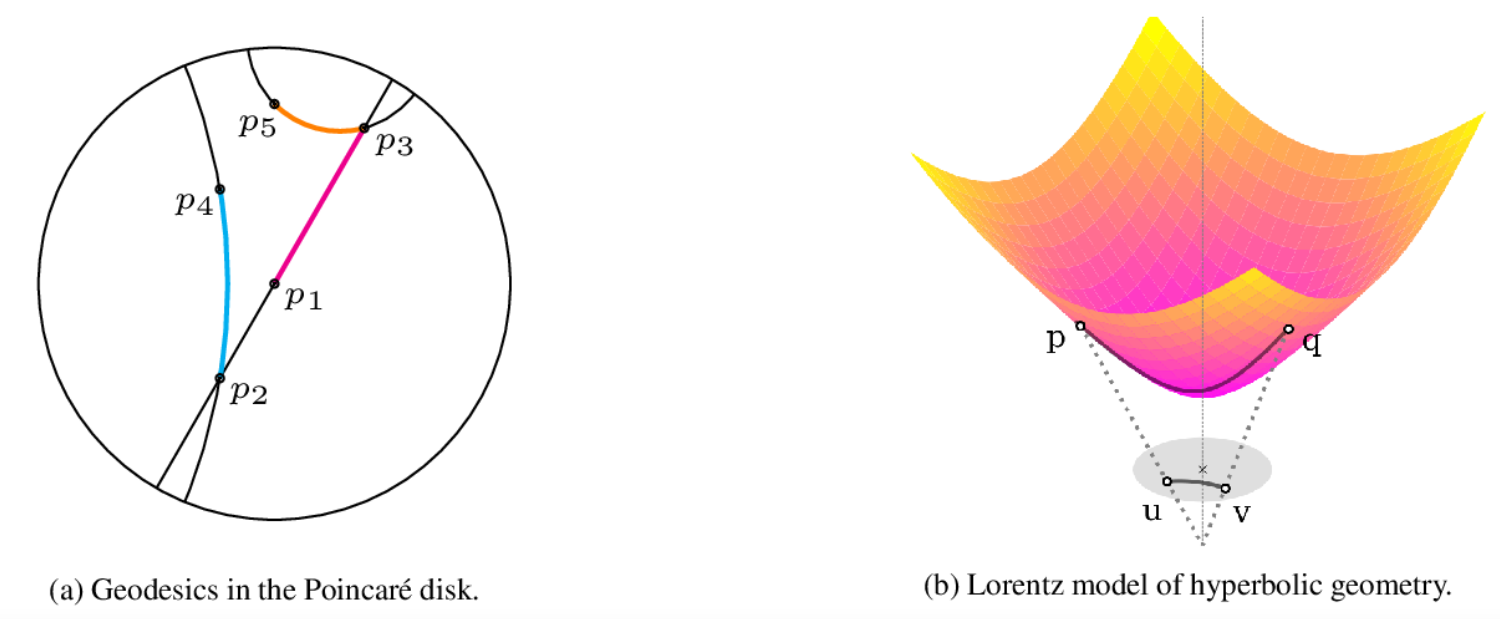
Nickel, M.; Kiela, D. Learning Continuous Hierarchies in the Lorentz Model of Hyperbolic Geometry. In Proceedings of the 35th International Conference on Machine Learning (ICML 2018), Stockholm, Sweden, 10–15 July 2018; mlr.press: Stockholm, Sweden, 2018; Volume 80, pp. 3776–3785.
1.4 Hyperbolic Graph Convolutional Neural Networks
**摘要:**图卷积神经网络(GCNs)将图中的节点嵌入到欧几里得空间中,已经显示在嵌入具有无标度或层次结构的现实世界图时会产生较大的失真。双曲几何提供了一种激动人心的替代方案,因为它能够实现较小失真的嵌入。然而,将GCNs扩展到双曲几何面临几个独特的挑战,因为目前尚不清楚如何在双曲空间中定义神经网络操作,例如特征转换和聚合。此外,由于输入特征通常是欧几里得的,如何将这些特征转换为具有正确曲率的双曲嵌入也不明确。在这里,我们提出了双曲图卷积神经网络(HGCN),这是第一个归纳式的双曲GCN,充分利用了GCNs和双曲几何的表达能力,以学习层次化和无标度图的归纳节点表示。我们在双曲空间的双曲模型中推导了GCNs操作,并将欧几里得输入特征映射到每一层具有不同可训练曲率的双曲空间中。实验证明,HGCN学习到的嵌入保留了层次结构,并在与欧几里得模拟相比表现出更好的性能,即使是在非常低维度的嵌入情况下:与最先进的GCNs相比,HGCN在链接预测的ROC AUC上实现了高达63.1%的误差降低,节点分类的F1分数降低了最高达47.5%,还在Pubmed数据集上改进了最新技术水平。
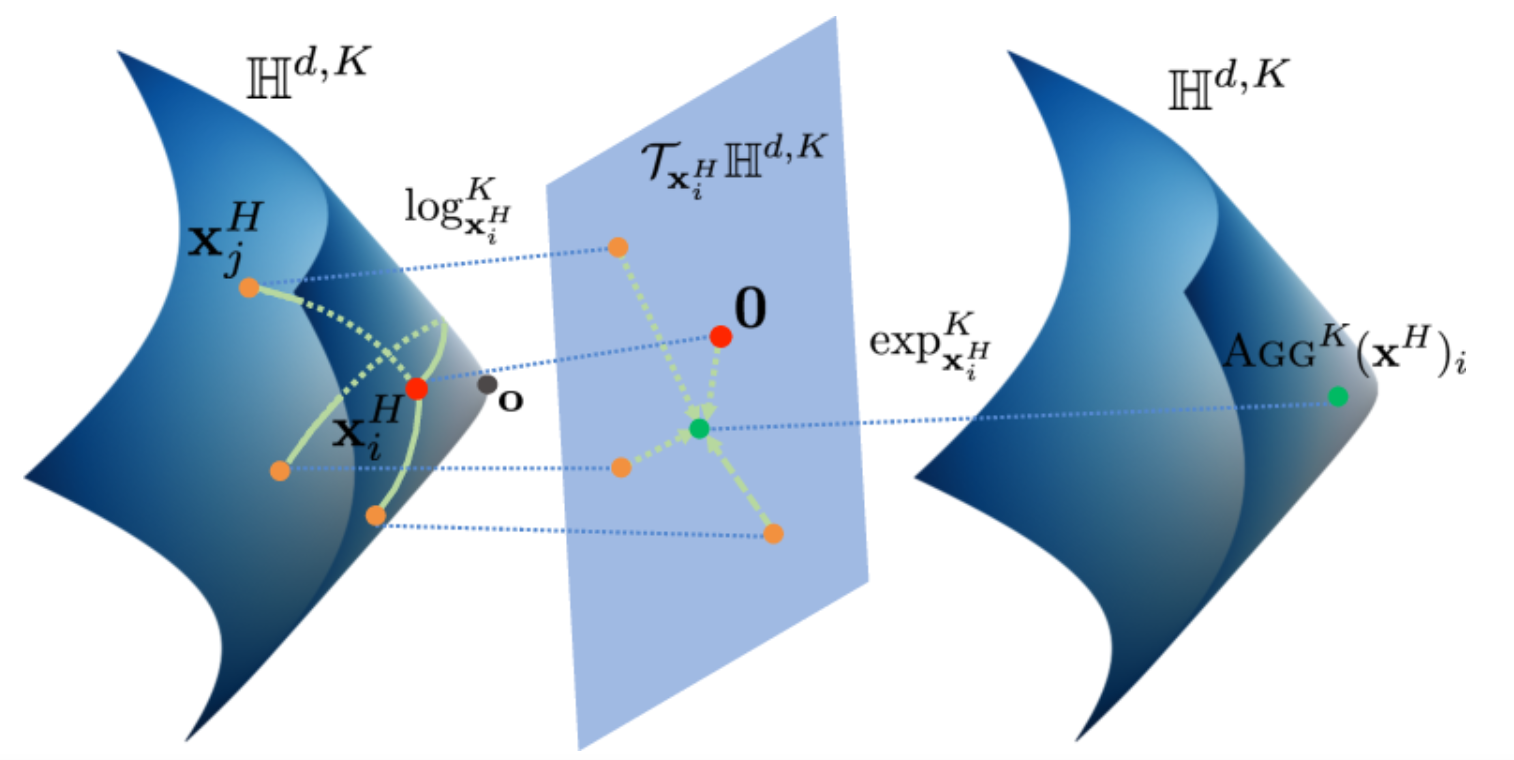
- 相较于在欧式空间做图卷积操作,在双曲空间效果更好
Chami, I.; Ying, Z.; Ré, C.; Leskovec, J. Hyperbolic Graph Convolutional Neural Networks. In Proceedings of the 32nd Annual Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; NeurIPS: Vancouver, BC, Canada, 2019; pp. 4869–4880.
1.5 Lorentzian Graph Convolutional Networks
摘要:图卷积神经网络(GCNs)将图中的节点嵌入到欧几里得空间中,已经显示在嵌入具有无标度或层次结构的现实世界图时会产生较大的失真。双曲几何提供了一种激动人心的替代方案,因为它能够实现较小失真的嵌入。然而,将GCNs扩展到双曲几何面临几个独特的挑战,因为目前尚不清楚如何在双曲空间中定义神经网络操作,例如特征转换和聚合。此外,由于输入特征通常是欧几里得的,如何将这些特征转换为具有正确曲率的双曲嵌入也不明确。在这里,我们提出了双曲图卷积神经网络(HGCN),这是第一个归纳式的双曲GCN,充分利用了GCNs和双曲几何的表达能力,以学习层次化和无标度图的归纳节点表示。我们在双曲空间的双曲模型中推导了GCNs操作,并将欧几里得输入特征映射到每一层具有不同可训练曲率的双曲空间中。实验证明,HGCN学习到的嵌入保留了层次结构,并在与欧几里得模拟相比表现出更好的性能,即使是在非常低维度的嵌入情况下:与最先进的GCNs相比,HGCN在链接预测的ROC AUC上实现了高达63.1%的误差降低,节点分类的F1分数降低了最高达47.5%,还在Pubmed数据集上改进了最新技术水平。

- 双曲图神经网络HGCN,在Pubmed数据集上比GCN效果更好
Zhang, Y.; Wang, X.; Shi, C.; Liu, N.; Song, G. Lorentzian Graph Convolutional Networks. In Proceedings of the The Web Conference (WWW 2021), Ljubljana, Slovenia, 19–23 April 2021; ACM/IW3C2: Ljubljana, Slovenia, 2021; pp. 1249–1261.
2. Spherical models
2.1 Geometry Interaction Knowledge Graph Embeddings
**摘要:**知识图谱(KG)嵌入在学习实体和关系表示以进行链接预测任务方面展现了强大的能力。先前的工作通常将KG嵌入到单一几何空间,如欧几里得空间(零曲率)、双曲空间(负曲率)或超球面空间(正曲率),以保持其特定的几何结构(例如链状、层次和环状结构)。然而,KG的拓扑结构似乎很复杂,因为它可能同时包含多种类型的几何结构。因此,无论是欧几里得空间、双曲空间还是超球面空间,将KG嵌入到单一空间中都无法准确捕捉KG的复杂结构。为了克服这一挑战,我们提出了几何交互知识图谱嵌入(GIE),它在欧几里得、双曲和超球面空间之间学习空间结构的交互。从理论上讲,我们提出的GIE能够捕捉更丰富的关系信息,模拟关键推理模式,并实现实体之间的表达性语义匹配。在三个成熟的知识图谱完成基准上的实验证明,我们的GIE在参数更少的情况下实现了最先进的性能。
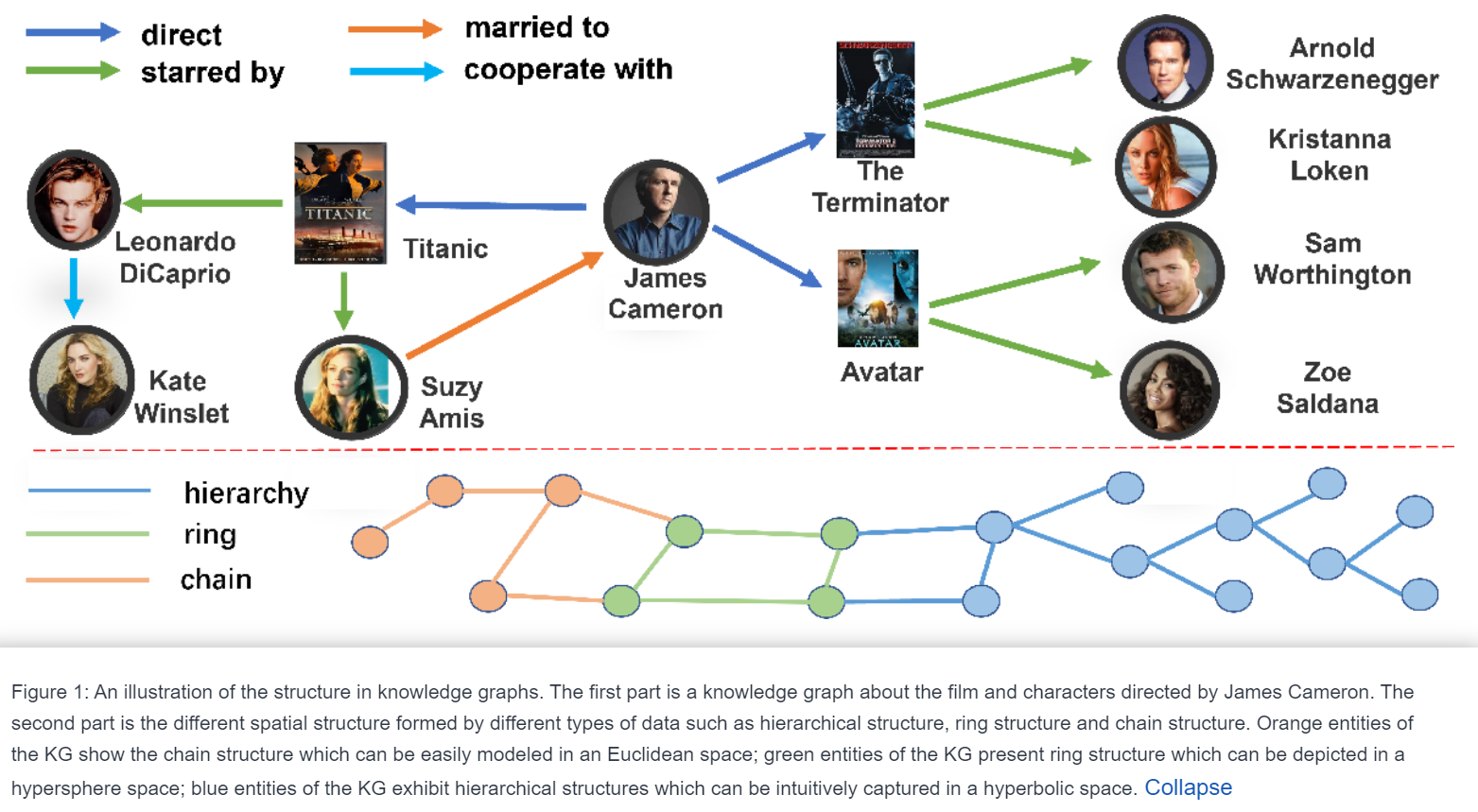
- 在欧几里得、双曲和超球面空间之间学习空间结构的交互信息,从而捕获更丰富的语义关系。
Cao, Z.; Xu, Q.; Yang, Z.; Cao, X.; Huang, Q. Geometry Interaction Knowledge Graph Embeddings. In Proceedings of the 36th Conference on Artificial Intelligence (AAAI 2022), Virtual Event, 22 February–1 March 2022; AAAI Press: Virtual Event, 2022; pp. 5521–5529.
2.2 Hyperbolic Geometry of Complex Networks
**摘要:**我们开发了一个几何框架来研究复杂网络的结构和功能。我们假设这些网络基于双曲几何,并且我们展示了在这个假设下,复杂网络中的异质度分布和强聚类自然地作为底层双曲几何的负曲率和度量性质的简单反映而出现。反之,我们表明如果一个网络具有一些度量结构,并且网络度分布是异质的,那么网络底层存在有效的双曲几何。然后,我们建立了我们的几何框架与复杂网络的统计力学之间的映射。这个映射将网络中的边解释为非相互作用的费米子,它们的能量是节点之间的双曲距离,而与边耦合的辅助场是这些能量或距离的线性函数。几何网络合集包含标准配置模型和经典随机图,它们是两种极限情况,具有退化的几何结构。最后,我们表明,由我们的几何框架可能实现的无需全局拓扑知识的有针对性的传输过程在网络中效率最大,根据所有效率度量,特别是在具有最强异质性和聚类的网络中,而且这种效率对于即使是对网络结构的灾难性干扰和损害也异常稳健。
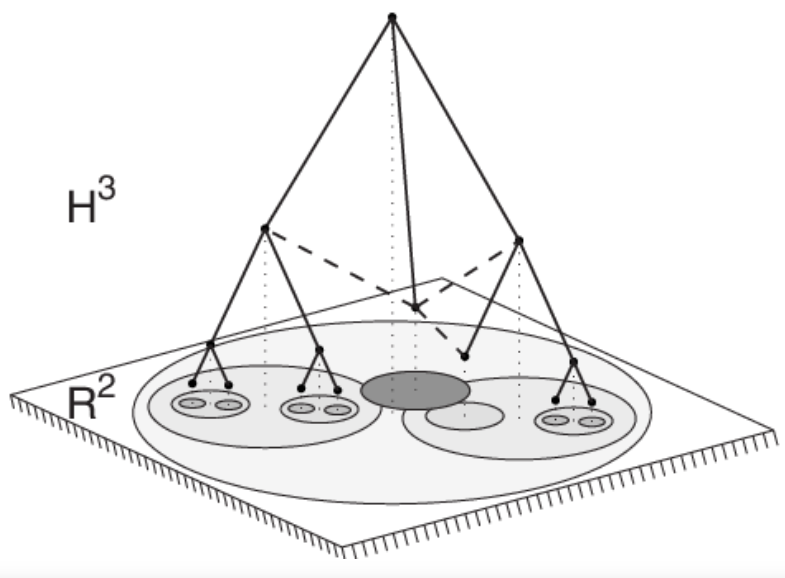
- 基于球面模型来做图嵌入,通过指数函数组合来自不同空间的嵌入分量,得到每个实体的嵌入。
Krioukov, D.V.; Papadopoulos, F.; Kitsak, M.; Vahdat, A.; Boguñá, M. Hyperbolic Geometry of Complex Networks. arXiv 2010,arXiv:1006.5169.
2.3 DeepSphere: A graph-based spherical CNN
**摘要:**为球形神经网络设计卷积需要在效率和旋转等变性之间进行精细的权衡。DeepSphere是一种基于球面离散表示的图方法,能够在这两个愿望之间实现可控的平衡。这个贡献是双重的。首先,我们从理论和经验上研究了等变性如何受底层图的影响,特别是关于像素数和邻居数量。其次,我们在相关问题上评估了DeepSphere的性能。实验证明了其在效率和灵活性方面表现出的最新技术水平,并展示了这种表述的优越性。或许令人惊讶的是,与先前的工作相比,结果表明各向异性滤波器可能是一个不必要的代价。
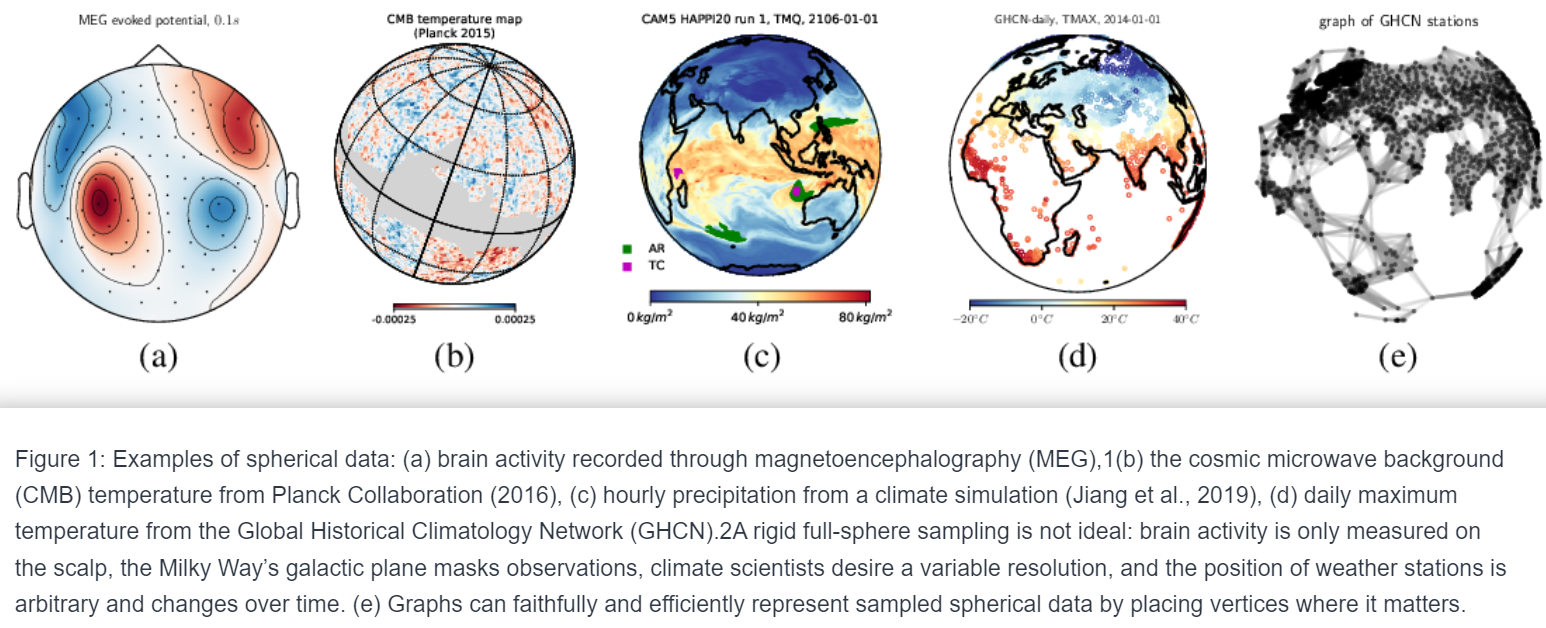
- 基于球面离散表示的图方法在效率和灵活性达到最佳
Defferrard, M.; Milani, M.; Gusset, F.; Perraudin, N. DeepSphere: A graph-based spherical CNN. In Proceedings of the 8th International Conference on Learning Representations (ICLR 2020), Addis Ababa, Ethiopia, 26–30 April 2020; OpenReview.net: Addis Ababa, Ethiopia, 2020.
3. Gaussian Embedding Models
3.1 Deep Variational Network Embedding in Wasserstein Space
**摘要:**网络嵌入旨在将网络嵌入到低维向量空间中,同时保留网络的固有结构属性,近年来引起了相当大的关注。现有的大多数嵌入方法将节点嵌入为低维连续空间中的点向量。这样,边的形成是确定性的,仅由节点的位置决定。然而,现实世界网络的形成和演化充满了不确定性,使得这些方法并非最优。为解决这个问题,本文提出了一种新颖的Wasserstein空间中的深度变分网络嵌入(DVNE)。所提出的方法在Wasserstein空间中学习每个节点的高斯分布作为潜在表示,可以同时保留网络结构并建模节点的不确定性。具体而言,我们使用2-Wasserstein距离作为分布之间的相似性度量,可以很好地在网络中保留传递性,并具有线性计算成本。此外,我们的方法通过深度变分模型暗示了均值和方差的数学关系,通过均值向量很好地捕捉了节点的位置,并通过方差捕捉了节点的不确定性。此外,我们的方法通过保留网络中的一阶和二阶接近性,捕捉了局部和全局网络结构。我们的实验结果表明,与最先进的方法相比,我们的方法可以有效地建模网络中节点的不确定性,并在诸如链接预测和多标签分类等实际应用中取得了显著的增益。

- 深度变分网络嵌入模型(DVNE)保持基于自编码器架构的分布之间的相似性,旨在在瓦瑟斯坦空间(Wasserstein space)中保持一阶和二阶的接近性。
Zhu, D.; Cui, P.; Wang, D.; Zhu, W. Deep Variational Network Embedding in Wasserstein Space. In Proceedings of the 24th International Conference on Knowledge Discovery & Data Mining (KDD 2018), London, UK, 19–23 August 2018; Guo, Y., Farooq, F., Eds.; ACM: London, UK, 2018; pp. 2827–2836.
3.2 Multilabel Classification on Heterogeneous Graphs with Gaussian Embeddings
**摘要:**我们考虑在异构图中进行节点分类的问题,其中节点和关系都可能是不同类型的,并且每种节点类型都关联着不同的类别集。尽管图节点分类主要是针对同质图进行的,但异构分类是一个近期的问题,其动机来自于社交网络等领域的应用,其中图本质上是异构的。我们提出了一种基于学习图嵌入的这个问题的推断方法,并使用高斯嵌入来建模与节点表示相关的不确定性。在三个异构数据集上提供了与代表性基线方法的比较。
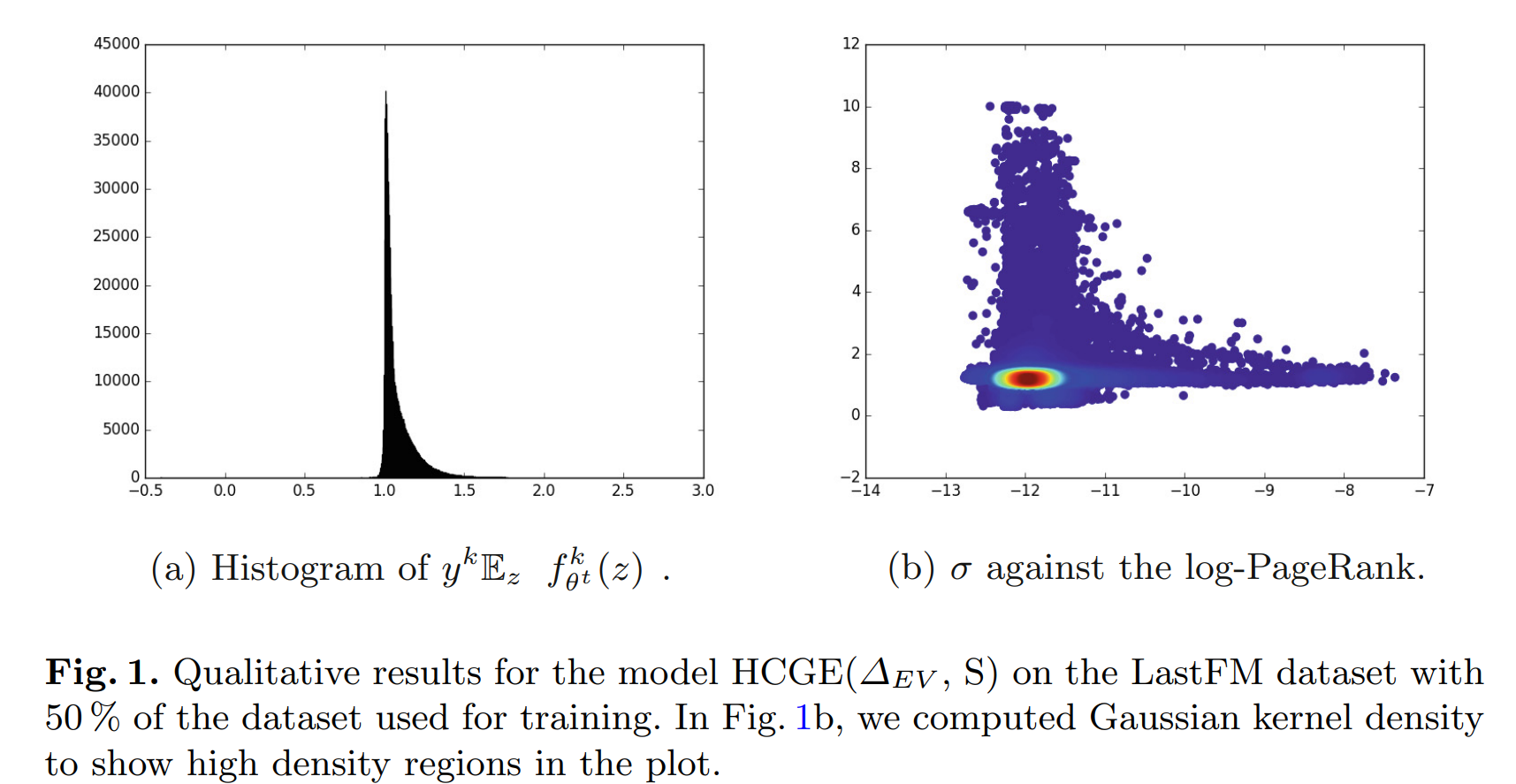
- 使用高斯嵌入来建模与节点表示相关的不确定性
Santos, L.D.; Piwowarski, B.; Gallinari, P. Multilabel Classification on Heterogeneous Graphs with Gaussian Embeddings. In Proceedings of the Machine Learning and Knowledge Discovery in Databases—European Conference (ECML PKDD 2016), Riva del Garda, Italy, 19–23 September 2016; Springer: Riva del Garda, Italy, 2016; Volume 9852, pp. 606–622.
3.3 Deep Gaussian Embedding of Graphs: Unsupervised Inductive Learning via Ranking
- **摘要:**在网络分析中,学习图中节点表示的方法在许多下游学习任务中发挥着至关重要的作用。我们提出了Graph2Gauss - 一种能够在大规模(带属性)图上高效学习多功能节点嵌入的方法,该方法在诸如链接预测和节点分类等任务中表现出色。与大多数将节点表示为低维连续空间中的点向量的方法不同,我们将每个节点嵌入为一个高斯分布,从而能够捕捉关于表示的不确定性。此外,我们提出了一种处理归纳学习场景并适用于不同类型图的无监督方法:普通/带属性、有向/无向。通过利用网络结构和相关节点属性,我们能够在没有额外训练的情况下对未见过的节点进行泛化。为了学习嵌入,我们采用了一个个性化的排名公式,根据节点之间的距离,利用网络结构所施加的自然排序。对真实世界网络的实验证明了我们方法的高性能,在多个不同任务上胜过了最先进的网络嵌入方法。此外,我们演示了建模不确定性的好处 - 通过分析不确定性,我们可以估计邻域的多样性并检测图的固有潜在维度。

- 提出基于高斯空间的Graph2Gauss,能在大规模图上高效学习多功能节点嵌入的方法。
Bojchevski, A.; Günnemann, S. Deep Gaussian Embedding of Graphs: Unsupervised Inductive Learning via Ranking. In Proceedings of the 6th International Conference on Learning Representations (ICLR 2018), Vancouver, BC, Canada, 30 April–3 May 2018; OpenReview.net: Vancouver, BC, Canada, 2018.
3.4 Learning to Represent Knowledge Graphs with Gaussian Embedding
- **摘要:**最近,知识图谱(KG)在潜在空间的表示引起了越来越多的关注。为此,一些提出的模型(例如TransE)通过优化全局损失函数,将KG的实体和关系嵌入到一个“点”向量空间中,确保正三元组的分数高于负三元组。我们注意到这些模型总是以相同的方式对待所有实体和关系,忽略它们的(不)确定性。实际上,不同的实体和关系可能包含不同的确定性,使得相同的确定性不足以建模。因此,本文转向基于密度的嵌入,并提出了KG2E,用于明确地建模实体和关系的确定性,该方法在多维高斯分布空间中学习KG的表示。每个实体/关系都由一个高斯分布表示,其中均值表示其位置,协方差(目前采用对角协方差)可以正确表示其确定性。此外,与点状方法中使用的对称度量相比,我们使用KL散度来评分三元组,这是一种自然的非对称函数,可以有效地建模多种类型的关系。我们在多个基准数据集(WordNet和Freebase)上进行了广泛的链接预测和三元组分类实验。我们的实验结果表明,我们的方法能够有效地建模KG中实体和关系的(不)确定性,并在性能上显著优于最先进的方法(包括TransH和TransR)。
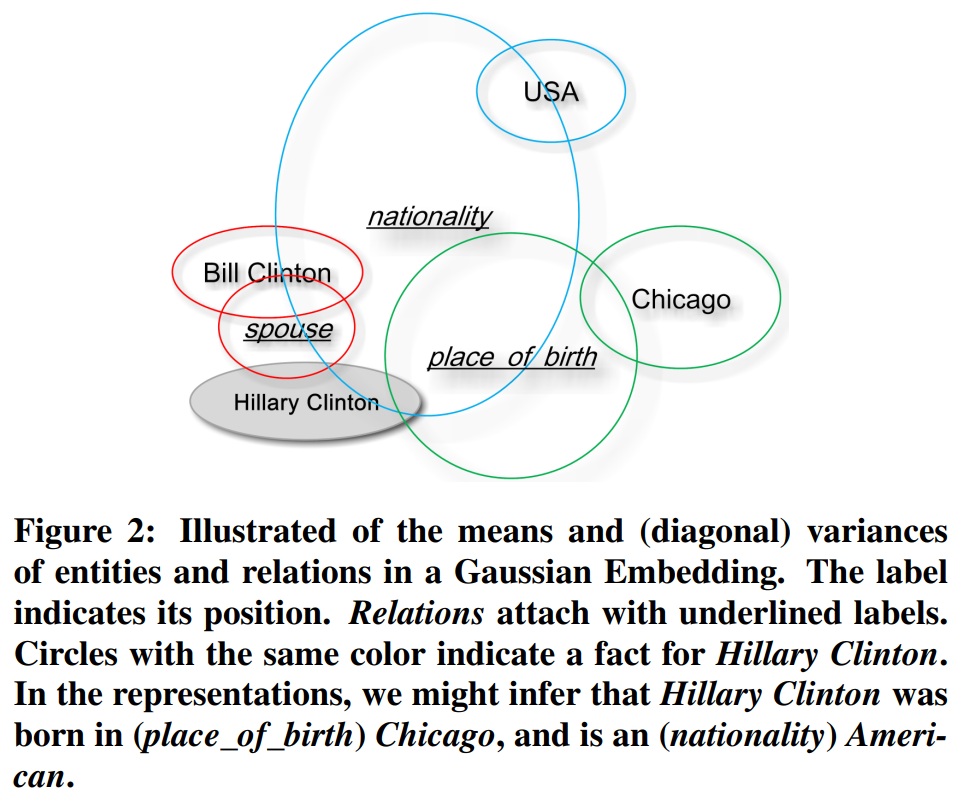
- 该模型在多维高斯分布空间中学习知识图谱的表示,能够有效实体和关系的不确定性。
He, S.; Liu, K.; Ji, G.; Zhao, J. Learning to Represent Knowledge Graphs with Gaussian Embedding. In Proceedings of the 24th International Conference on Information and Knowledge Management (CIKM 2015), Melbourne, VIC, Australia, 19–23 October 2015; ACM: Melbourne, VIC, Australia, 2015; pp. 623–632.
相关文章:

【论文合集】在非欧空间中的图嵌入方法(Graph Embedding in Non-Euclidean Space)
文章目录 1. Hyperbolic Models1.1 Hyperbolic Graph Attention Network1.2 Poincar Embeddings for Learning Hierarchical Representations.1.3 Learning Continuous Hierarchies in the Lorentz Model of Hyperbolic Geometry1.4 Hyperbolic Graph Convolutional Neural Net…...
锐捷EWEB网管系统 RCE漏洞复现
0x01 产品简介 锐捷网管系统是由北京锐捷数据时代科技有限公司开发的新一代基于云的网络管理软件,以“数据时代创新网管与信息安全”为口号,定位于终端安全、IT运营及企业服务化管理统一解决方案。 0x02 漏洞概述 Ruijie-EWEB 网管系统 flwo.control.php 中的 type 参数存在…...

Clickhouse在货品标签场景的应用
背景 在电商场景中,我们经常需要对货品进行打标签的操作,简单来说就是对货品进行各种分类,按照价格段进行分组,此时运营人员就可以通过价格段捞取到满足条件的商品了,本文就来简单看下这个场景如何在clickhouse中实现…...

CentOS 7 lvm 更换坏盘操作步骤小记 —— 筑梦之路
背景介绍 硬盘容量不足、硬盘坏道太多等不可控的原因需要更换,要求不能丢失数据进行无损替换硬盘。 操作步骤 1. 将硬盘插入机器,上电连接到服务器 2. 在centos 7 系统中检测是否识别出来硬盘 lsblk 3. 给新插入的硬盘分区 parted /dev/sdc mklabel g…...

zabbix的自动发现和注册、proxy代理和SNMP监控
目录 一、zabbix自动发现与自动注册机制: 1、概念 2、zabbix 自动发现与自动注册的部署 二、zabbix的proxy代理功能: 1、工作流程 2、安装部署 三、zabbix-snmp 监控 1、概念 2、安装部署 四、总结: 一、zabbix自动发现与自动注册…...

以Hub为中心节点的网络技术探析
在计算机网络中,Hub是一个重要的组成部分,它作为中心节点,连接着各个站点,实现数据的传输和通信。本文将对以Hub为中心节点的网络进行深入的技术探析。 首先,我们需要了解什么是Hub。在网络术语中,Hub通常…...

百度推送收录工具-免费的各大搜索引擎推送工具
在互联网时代,网站收录是网站建设的重要一环。百度推送工具作为一种提高网站收录速度的方式备受关注。在这个信息爆炸的时代,对于网站管理员和站长们来说,了解并使用一些百度推送工具是非常重要的。本文将重点分享百度批量域名推送工具和百度…...
物流实时数仓ODS层——Mysql到Kafka
目录 1.采集流程 2.项目架构 3.resources目录下的log4j.properties文件 4.依赖 5.ODS层——OdsApp 6.环境入口类——CreateEnvUtil 7.kafka工具类——KafkaUtil 8.启动集群项目 这一层要从Mysql读取数据,分为事实数据和维度数据,将不同类型的数据…...

奇迹mu 架设过程中可能会出现的问题及解决办法
通常我们在架设奇迹的时候,可能会遇见这种问题那种问题,很多用户都不知道该如何解决,今天我们就来系统的说明一下一些常见的问题,帮助遇见这些问题的用户理清一个架设的思路,更清楚的判断问题出在哪里,该如…...
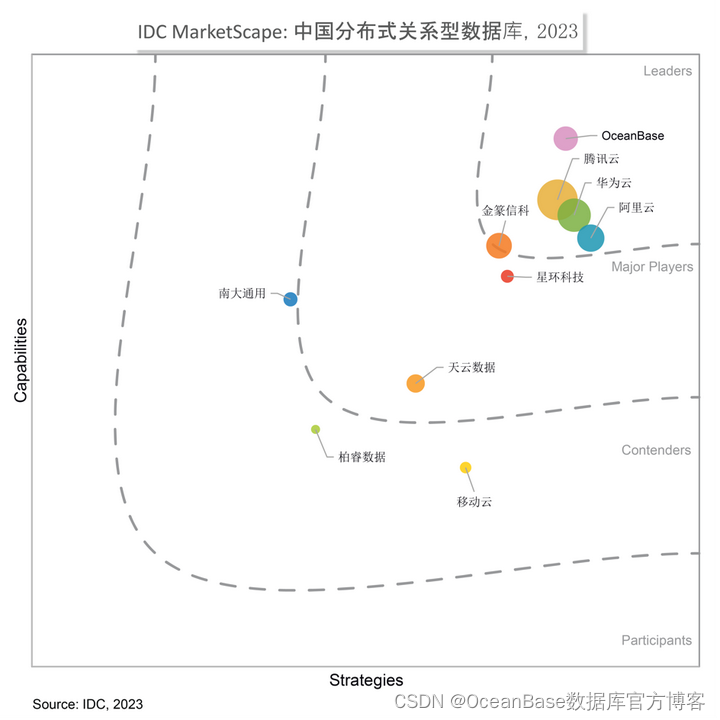
IDC MarketScape2023年分布式数据库报告:OceanBase位列“领导者”类别,产品能力突出
12 月 1 日,全球领先的IT市场研究和咨询公司 IDC 发布《IDC MarketScape:中国分布式关系型数据库2023年厂商评估》(Document number:# CHC50734323)。报告认为,头部厂商的优势正在扩大,OceanBase 位列“领导者”类别。…...

Docker创建mqtt容器mosquitto
#1.创建映射到主机的配置文件/bwss/agent/docker/mosquitto_public/config/mosquitto.conf 内容为: listener 51883 0.0.0.0 # 0.0.0.0 allow_anonymous false persistence false persistence_location /mosquitto/data password_file /mosquitto/config/passwd …...
运维知识点-SQLServer/mssql
SQLServer/mssql Microsoft structed query language常见注入提权 技术点:0x00 打点前提 0x01 上线CS0x02 提权0x03 转场msf0x04 抓取Hash0x05 清理痕迹 Microsoft structed query language 常见注入 基于联合查询注入 order by 判断列数(对应数据类型…...

Reactor实战,创建一个简单的单线程Reactor(理解了就相当于理解了多线程的Reactor)
单线程Reactor package org.example.utils.echo.single;import java.io.IOException; import java.net.InetSocketAddress; import java.nio.channels.*; import java.util.Iterator; import java.util.Set;public class EchoServerReactor implements Runnable{Selector sele…...
)
NoSQL大数据存储技术测试题(参考答案)
目录 1.绪论 2.NoSQL数据库的基本原理 4.HBase的基本原理与使用 5.HBase高级原理 7.MongoDB 8.其他NoSQL数据库 1.绪论 总分: 14.0 10分 单项选择题 4分 判断题 教师评语: 一 单项选择题(10分) 1、NoSQL一词表示的含义是()。…...

Python查看文件列表
os.listdir 是 Python 的一个内置函数,用于列出指定目录中的所有文件和子目录。它接受一个字符串参数,即要列出内容的目录的路径。 列出当前工作目录中的所有文件和子目录 files_and_dirs os.listdir() print(files_and_dirs) 列出指定目录中的所…...
INA219电流感应芯片_程序代码
详细跳转借鉴链接INA219例程此处进行总结 简单介绍一下 INA219: 1、 输入脚电压可以从 0V~26V,INA219 采用 3.3V/5V 供电. 2、 能够检测电流,电压和功率,INA219 内置基准器和乘法器使之能够直接以 A 为单位 读出电流值。 3、 16 位可编程地…...

FlinkSql-Temporal Joins-Lookup Join
说明 在 Flink SQL 中,Temporal Joins 是一种常见的数据关联操作,特别适用于处理包含时间维度的数据。Lookup Join 是 Temporal Joins 的一种类型,它允许将流数据与维表数据进行关联。使用场景如下: 实时维度关联: 当…...
STM32之定时器
目录 1、定时器介绍 1.定时器工作原理 2.定时器的分类 3.通用定时器主要功能介绍 4.定时器计数模式 5.定时器时钟源 6.定时器溢出时间计算公式 2、定时器中断的实验 codeMX的配置 代码编写 1.使用到的HAL库函数 1.中断回调函数需要我们重写 2. 在中断模式下启动TIM…...
Canvas鼠标画线
鼠标按下开始画线,鼠标移动根据鼠标的轨迹去画,鼠标抬起停止画线 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0">…...
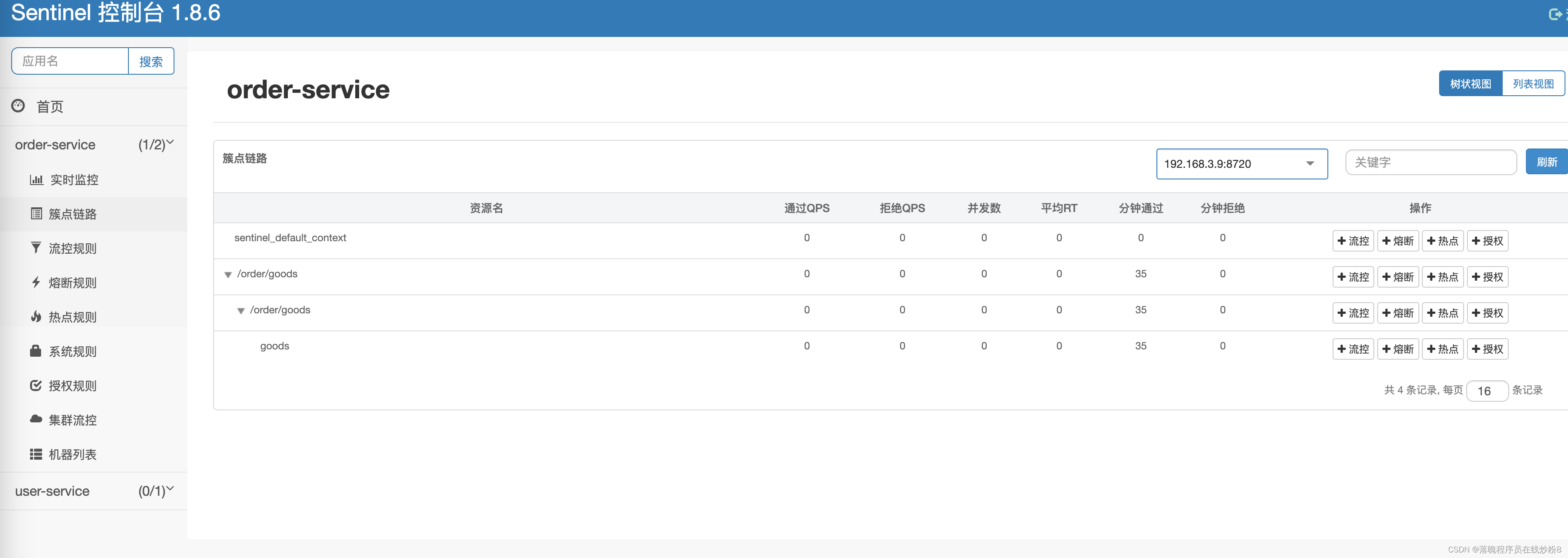
Docker 安装部署 Sentinel Dashboard
1、下载 jar 包 官方 jar 包下载地址:https://github.com/alibaba/Sentinel/releases 或者点击 链接 直接跳转到下载页 进入链接下载你需要的版本 下载完毕(我这里统一放在一个sentinel目录内) 2、编写 Dockerfile 文件(这里我不…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...
