排序之损失函数List-wise loss(系列3)
排序系列篇:
- 排序之指标集锦(系列1)
- 原创 排序之损失函数pair-wise loss(系列2)
- 排序之损失函数List-wise loss(系列3)

最早的关于list-wise的文章发表在Learning to Rank: From Pairwise Approach to Listwise Approach中,后面陆陆续续出了各种变形,但是也是万变不离其宗,本文梳理重在原理。
论文链接listNet,参考的实现代码:实现代码
1. 为什么要List-wise loss
pairwise优缺点
优点:
- 一些已经被验证的较好的分类模型可以直接拿来用。
- 在一些特定场景下,其pairwise features 很容易就可以获得。
缺点:
- 其学习的目标是最小化文档对的分类错误,而不是最小化文档排序的错误。学习目标和实际目标(MAE,NDCG)有所违背。
- 训练过程可能是极其耗时的,因为生成的文档对样本数量可能会非常多。
那么本篇论文是如何解决这些问题呢?
在pointwise 中,我们将每一个<query, document> 作为一个训练样本来训练一个分类模型。这种方法没有考虑文档之间的顺序关系;而在pariwise 方法中考虑了同一个query 下的任意两个文档的相关性,但同样有上面已经讲过的缺点;在listwise 中,我们将一个<query,documents> 作为一个样本来训练,其中documents 为与这个query 相关的文件列表。
论文中还提出了概率分布的方法来计算listwise 的损失函数。并提出了permutation probability 和top one probability 两种方法。下面会详述这两种方法。
2. 方法介绍
2.1. loss输入格式
假设我们有m 个 querys:
Q=(q(1),q(2),q(3),...,q(m))Q=(q^{(1)}, q^{(2)}, q^{(3)},...,q^{(m)}) Q=(q(1),q(2),q(3),...,q(m))
每个query 下面有n 个可能与之相关的文档(对于不同的query ,其n 可能不同)
d(i)=(d1(i),d2(i),...,dn(i))d^{(i)} = (d^{(i)}_1, d^{(i)}_2, ..., d^{(i)}_n)d(i)=(d1(i),d2(i),...,dn(i))
对于每个query 下的所有文档,我们可以根据具体的应用场景得到每个文档与query 的真实相关度得分。
y(i)=(y1(i),y2(i),....,yn(i))y^{(i)} = (y^{(i)}_1, y^{(i)}_2, ...., y^{(i)}_n)y(i)=(y1(i),y2(i),....,yn(i))
我们可以从每一个文档对(q(i),dj(i))(q^{(i)}, d^{(i)}_{j})(q(i),dj(i))得到该文档的打分,q(i)q^{(i)}q(i)与文档集合d(i)d^{(i)}d(i)中的每个文档打分,可以得到该query 下的所有文档的特征向量:
x(i)=(x1(i),x2(i),...,xn(i))x^{(i)} = (x^{(i)}_1, x^{(i)}_2, ..., x^{(i)}_n)x(i)=(x1(i),x2(i),...,xn(i))
并且在已知每个文档真实相关度得分的条件下:
y(i)=(y1(i),y2(i),...,yn(i))y^{(i)} = (y^{(i)}_1, y^{(i)}_2, ..., y^{(i)}_n)y(i)=(y1(i),y2(i),...,yn(i))
我们可以构建训练样本:
T={(x(i),y(i))}T=\begin{Bmatrix} (x^{(i)}, y^{(i)}) \end{Bmatrix}T={(x(i),y(i))}
要特别注意的是:这里面一个训练样本是(x(i),y(i))(x^{(i)}, y^{(i)})(x(i),y(i)),而这里的x(i)x^{(i)}x(i)是一个与query 相关的文档列表,这也是区别于pointwise 和pairwise 的一个重要特征。
关于y(i)y^{(i)}y(i)paper里面的相关描述:
2.2. loss计算
那么有训练样本了,如何计算loss 呢?
假设我们已经有了排序函数 f ff,我们可以计算特征向量x(i)x^{(i)}x(i)的得分情况:
z(i)=(f(x1(i)),f(x2(i)),...,f(xn(i)))z^{(i)} = (f(x_1^{(i)}), f(x_2^{(i)}), ..., f(x_n^{(i)}))z(i)=(f(x1(i)),f(x2(i)),...,f(xn(i)))
显然我们学习的目标就是,最小化真实得分和预测得分的误差:
∑i=1mL(y(i),z(i))\sum_{i=1}^{m} L(y^{(i)}, z^{(i)})i=1∑mL(y(i),z(i))
L 为 listwise 的损失函数。
2.2.1. 概率模型
假设对于某一个query 而言,与之可能相关的文档有{1,2,3,...,n}\{1, 2, 3, ..., n\}{1,2,3,...,n},假设某一种排序的结果为π\piπ
π=<π(1),π(2),..,π(n)>\pi=<\pi(1), \pi(2), .., \pi(n)>π=<π(1),π(2),..,π(n)>
对于n 个文档,有n! 种排列情况。这所有的排序情况记为Ωn\Omega_nΩn。假设已有排序函数,那么对于每个文档,我们都可以计算出相关性得分s=(s1,s2,...,sn)s = (s_1, s_2, ..., s_n)s=(s1,s2,...,sn)。 显然对于每一种排序情况,都是有可能发生的,但是每一种排列都有其最大似然值。
我们可以这样定义某一种排列π\piπ的概率(最大似然值):
Ps(π)=∏j=1nϕ(sπ(j))∑k=jnϕ(sπ(k))P_s(\pi) = \prod_{j=1}^{n} \frac{\phi (s_{\pi(j)})}{\sum_{k=j}^{n}\phi(s_{\pi(k)})}Ps(π)=j=1∏n∑k=jnϕ(sπ(k))ϕ(sπ(j))
其中ϕ\phiϕ表示对分数的归一化处理。
例如有三个文档π=<1,2,3>\pi = <1,2,3>π=<1,2,3> ,其排序函数计算每个文档得分为s=(s1,s2,s3)s=(s_1, s_2, s_3)s=(s1,s2,s3),则该种排序概率为:
Ps(π)=ϕ(s1)ϕ(s1)+ϕ(s2)+ϕ(s3)⋅ϕ(s2)ϕ(s2)+ϕ(s3)⋅ϕ(s3)ϕ(s3)P_s(\pi) =\frac{\phi(s_1)}{\phi(s_1)+\phi(s_2)+\phi(s_3)} \cdot \frac{\phi(s_2)}{\phi(s_2)+\phi(s_3)} \cdot \frac{\phi(s_3)}{\phi(s_3)}Ps(π)=ϕ(s1)+ϕ(s2)+ϕ(s3)ϕ(s1)⋅ϕ(s2)+ϕ(s3)ϕ(s2)⋅ϕ(s3)ϕ(s3)
对于另外一种排序,例如π′=<3,2,1>{\pi}' = <3,2,1>π′=<3,2,1> ,则这种排列概率为:
Ps(π)=ϕ(s3)ϕ(s3)+ϕ(s2)+ϕ(s1)⋅ϕ(s2)ϕ(s2)+ϕ(s3)⋅ϕ(s1)ϕ(s1)P_s(\pi) =\frac{\phi(s_3)}{\phi(s_3)+\phi(s_2)+\phi(s_1)} \cdot \frac{\phi(s_2)}{\phi(s_2)+\phi(s_3)} \cdot \frac{\phi(s_1)}{\phi(s_1)}Ps(π)=ϕ(s3)+ϕ(s2)+ϕ(s1)ϕ(s3)⋅ϕ(s2)+ϕ(s3)ϕ(s2)⋅ϕ(s1)ϕ(s1)
很明显,< 3,2,1 >这个排序的打分最低,< 1,2,3 >这个排序的打分最高。
2.2.2. Top K Probability
上面那种计算排列概率的方式,其计算复杂度达到n!n!n!,太耗时间,由此论文中提出了一种更有效率的方法 top one。我们在这里推广到top k来分析总结。
上面计算某一种排序方式概率:
Ps(π)=∏j=1nϕ(sπ(j))∑k=jnϕ(sπ(k))P_s(\pi) = \prod_{j=1}^{n} \frac{\phi (s_{\pi(j)})}{\sum_{k=j}^{n}\phi(s_{\pi(k)})} Ps(π)=j=1∏n∑k=jnϕ(sπ(k))ϕ(sπ(j))
排在第一位的有nnn 种情况,排在第二位的有n−1n−1n−1 种情况,后面依次类推。相当与利用 top nnn来计算。
那么 top K(K<n)K(K<n)K(K<n)计算:
Ps(π)=∏j=1Kϕ(sπ(j))∑k=jnϕ(sπ(k))P_s(\pi) = \prod_{j=1}^{K} \frac{\phi (s_{\pi(j)})}{\sum_{k=j}^{n}\phi(s_{\pi(k)})}Ps(π)=j=1∏K∑k=jnϕ(sπ(k))ϕ(sπ(j))
同理,这里的计算复杂度为n∗(n−1)∗(n−2)∗...∗(n−k+1)n∗(n−1)∗(n−2)∗...∗(n−k+1)n∗(n−1)∗(n−2)∗...∗(n−k+1),即为N!/(N−k)!N!/(N-k)!N!/(N−k)!种不同排列,大大减少了计算复杂度。
如果K=1K=1K=1,就蜕变成论文中top 1 的情况,此时有 n 种不同排列情况:
Ps(π)=ϕ(sπ(j))∑k=jnϕ(sπ(k))P_s(\pi) = \frac{\phi (s_{\pi(j)})}{\sum_{k=j}^{n}\phi(s_{\pi(k)})}Ps(π)=∑k=jnϕ(sπ(k))ϕ(sπ(j))
对于N!/(N−k)!N!/(N-k)!N!/(N−k)!种不同的排列情况,就有 N!/(N−k)! 个排列预测概率,就形成了一种概率分布,再由真实的相关性得分计算相应的排列概率,得到真实的排列概率分布。由此可以利用 cross−entropy 来计算两种分布的距离作为损失函数:
L(y(i),z(i))=−∑j=1n{Py(i)(j)∗log(Pz(i)(j))}L(y^{(i)}, z^{(i)}) = - \sum_{j=1}^{n} \{P_{y^{(i)}}(j) *log(P_{z^{(i)}}(j))\}L(y(i),z(i))=−j=1∑n{Py(i)(j)∗log(Pz(i)(j))}
例如一个查询下有三个文档<A,B,C><A,B,C><A,B,C>:

2.2.3. ListNet
这里给出ListNet最终的形式
在论文中,Listnet只是将上面的topKtopKtopK 中的ϕ\phiϕ函数变成 exp 函数:
Ps(π)=exp(sπ(j))∑k=jnexp(sπ(k))P_s(\pi) = \frac{\exp (s_{\pi(j)})}{\sum_{k=j}^{n}\exp(s_{\pi(k)})}Ps(π)=∑k=jnexp(sπ(k))exp(sπ(j))
这样不就是计算预测出的得分的softmax 了吗?实际上的确如此,在实现代码中就是这样做的,当时我直接看代码还一脸懵逼,这不就是对文档预测出来的得分做了个softmax 操作吗?跟top−one 有什么关系,仔细看论文才知道怎么回事。
top−1 时,只有n 种排列情况,这大大减少了计算量。如果top K(K>1)K (K>1)K(K>1),则需要计算的排列情况就会变多。
假设排序函数 f 的参数为w ,则 top-one 的排列概率分布为:
Pz(i)(fw)(xj(i))=exp(fw(xj(i)))∑k=jnexp(fw(xk(i)))P_{z^{(i)}(f_w)}(x_j^{(i)}) = \frac{\exp (f_w(x_j^{(i)}))}{\sum_{k=j}^{n}\exp(f_w(x_k^{(i)}))}Pz(i)(fw)(xj(i))=∑k=jnexp(fw(xk(i)))exp(fw(xj(i)))
这里还是需要注意:是将某一个查询下的所有可能与之相关的文档列表,作为一个样本来训练。
最终的损失函数:
L(y(i),z(i)(fw))=−∑j=1n{Py(i)(xj(i))∗log(Pz(i)(fw)(xj(i)))}L(y^{(i)}, z^{(i)}(f_w)) = - \sum_{j=1}^{n} \{P_{y^{(i)}}(x_j^{(i)}) *log(P_{z^{(i)}(f_w)}(x_j^{(i)}))\}L(y(i),z(i)(fw))=−j=1∑n{Py(i)(xj(i))∗log(Pz(i)(fw)(xj(i)))}
小编总结:
简单来说, Listwise的loss其实从本质上可以归纳如下:
step1: 对所有包含正样本和负样本的集合进行softmax; step2: 在用交叉熵对所有样本求和计算loss
但是从原理上来说,其实这只是一个为了计算速度的折中。另外交叉熵中的groundtruth,也就是上面的yj(i)y^{(i)}_jyj(i)打分,这样groundtruth打分越高的,如果预测误差大导致的loss越大,从而对实际为高分但是预测为低分的关注度更高,从而提高top的打分。
实现细节
在看源码的时候发现了一个细节,paper里面说的是交叉熵,但是在代码实现中我发现用的是交叉熵,也就是红色里面是KL散度,而绿色才是交叉熵。

总结
在pairwise 中,只考虑了两个文档对的相对先后顺序,却没有考虑文档出现在搜索列表中的位置,排在搜索站果前列的文档更为重要,如果前列文档出现判断错误,代价明显高于排在后面的文档。针对这个问题的改进思路是引入代价敏感因素,即每个文档对根据其在列表中的顺序具有不同的权重,越是排在前列的权重越大,即在搜索列表前列,如果排错顺序的话其付出的代价更高(评价指标NDCG); 而listwise 讲一个查询下的所有文档作为一个样本,因为要组合出不同的排列,得到其排列概率分布,来最小化与真实概率分布的误差,这里面就考虑了文档之间的各种顺序关系。很好的避免了这种情况。
从概率模型的角度定义损失函数。
在实做时,其实将一个query 下的的所有可能与之相关的n个doc作为一个训练样本(这时可以理解batch_size=n) ,一定要注意:在计算top_1 probability 时,是在一个query 内的所有文档做softmax ,而不是在当前正在训练的所有的样本内做。这是区别pointwise、pairwise 的重要不同之处。
参考链接:
论文分享— >Learning to Rank: From Pairwise Approach to Listwise Approach

相关文章:

排序之损失函数List-wise loss(系列3)
排序系列篇: 排序之指标集锦(系列1)原创 排序之损失函数pair-wise loss(系列2)排序之损失函数List-wise loss(系列3) 最早的关于list-wise的文章发表在Learning to Rank: From Pairwise Approach to Listwise Approach中,后面陆陆续续出了各种变形&#…...

js对象和原型、原型链的关系
JS的原型、原型链一直是比较难理解的内容,不少初学者甚至有一定经验的老鸟都不一定能完全说清楚,更多的"很可能"是一知半解,而这部分内容又是JS的核心内容,想要技术进阶的话肯定不能对这个概念一知半解,碰到…...
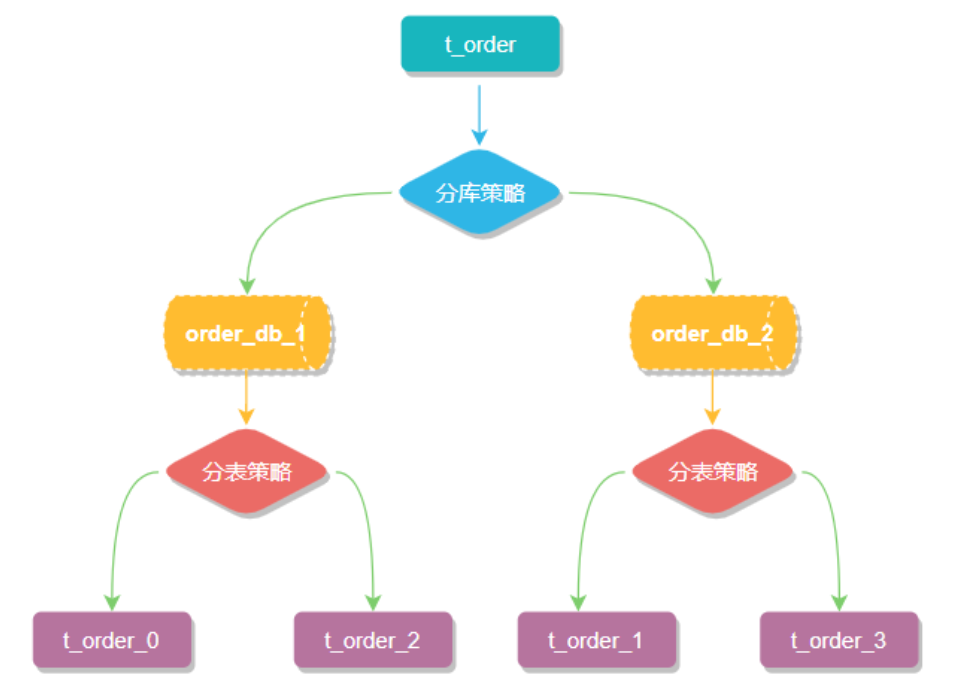
【SpringBoot高级篇】SpringBoot集成Sharding-JDBC分库分表
【SpringBoot高级篇】SpringBoot集成Sharding-JDBC分库分表Apache ShardingSphere分库分表分库分表的方式垂直切分垂直分表垂直分库水平切分水平分库水平分表分库分表带来的问题分库分表中间件Sharding-JDBCsharding-jdbc实现水平分表sharding-jdbc实现水平分库sharding-jdbc实…...

Shell特殊字符
shell语言,一些字符是有特殊意义的。 根据作用分为几种特殊符号 一、空白 shell调用函数,不像c语言那样用把参数放到括号里,用逗号分隔。而是用空格作为参数之间,参数与函数名之间的分隔符。 换行符也是特殊字符。换行符用作一条命…...

【计算机二级python】综合题目
计算机二级python真题 文章目录计算机二级python真题一、德国工业战略规划二、德国工业战略规划 第一问三、德国工业战略规划 第二问一、德国工业战略规划 描述:在右侧答题模板中修改代码,删除代码中的横线,填写代码,完成考试答案。…...

字节直播leader面
设计评论系统(缓存怎么做) mysql是否有主从延迟,如何解决 mysql有主从延迟 主从延迟主要因为mysql主从同步的机制,mysql有三种同步机制 同步复制:事务线程等待所有从库复制成功响应异步复制:事务不等待…...

PIC 单片机的时钟
注意:本文的内容无法保证绝对精确,后续可能会做改动,只是自己的笔记。这里的资料均源自数据手册本身。PIC18系列单片机的参考时钟可以选择三个基础时钟源:Primary Clock, OSC1 or OSC2,Secondary Clock,Inner clock.时钟源分为两个…...
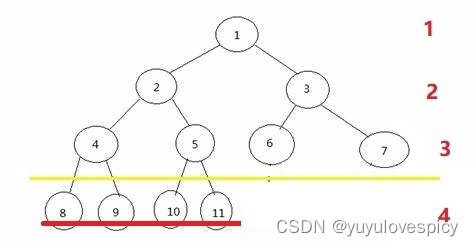
【数据结构】关于二叉树你所应该知道的数学秘密
目录 1.什么是二叉树(可以跳过 目录跳转) 2.特殊的二叉树(满二叉树/完全二叉树) 2.1 基础知识 2.2 满二叉树 2.3 完全二叉树 3.二叉树的数学奥秘(主体) 3.1 高度与节点个数 3.2* 度 4.运用二叉树的…...

哈希表题目:猜数字游戏
文章目录题目标题和出处难度题目描述要求示例数据范围解法一思路和算法代码复杂度分析解法二思路和算法代码复杂度分析题目 标题和出处 标题:猜数字游戏 出处:299. 猜数字游戏 难度 4 级 题目描述 要求 你在和朋友一起玩猜数字(Bulls…...
项目请求地址自动加上了本地ip的解决方式
一般情况下来说都是一些粗心大意的问题导致的 场景一:少加了/ 场景二:前后多加了空格 场景三:拼接地址错误
Vue3 企业级项目实战:项目须知与课程约定
本节内容很重要,希望大家能够耐心看完。 Vue3 企业级项目实战 - 程序员十三 - 掘金小册Vue3 Element Plus Spring Boot 企业级项目开发,升职加薪,快人一步。。「Vue3 企业级项目实战」由程序员十三撰写,2744人购买https://s.ju…...

传导EMI抑制-Π型滤波器设计
1 传导电磁干扰简介 在开关电源中,开关管周期性的通断会产生周期性的电流突变(di/dt)和电压突变(dv/dt),周期性的电流变化和电压变化则会导致电磁干扰的产生。 图1所示为Buck电路的电流变化,在Buck电路中上管电流和下…...

如何在excel中创建斐波那契数列
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:…...
遮挡检测--基于角度的遮挡检测方法
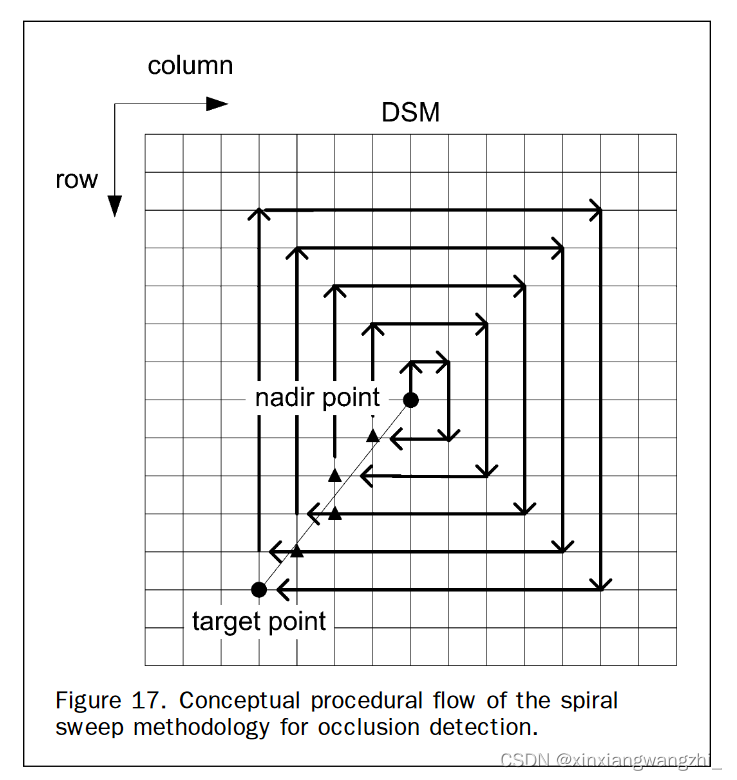
文章目录1基于角度的遮挡检测方法2遮挡检测遍历方法2.1方法1--自适应径向扫描方法2.2方法2--螺旋扫描法参考1基于角度的遮挡检测方法 在基于角度的方法中,通过依次分析DSM中沿径向方向的投影光线的角度来识别遮挡。定义α\alphaα角:DSM三维点与相机中心…...
)
【luogu CF1098D】Eels(结论)
Eels 题目链接:luogu CF1098D 题目大意 有一个可重集,每次操作会放进去一个数或者取出一个数。 然后每次操作完之后,问你对这个集合进行操作,每次选出两个数 a,b 加起来合并回去,直到集合中只剩一个数,要…...
【java】遍历文件夹输出所有文件的文件名与绝对路径,在windows环境
【java】遍历文件夹输出所有文件的文件名与绝对路径,在windows环境 String filepath "D:\\CloudMusic\\";//D盘下的file文件夹的目录File file new File(filepath);//File类型可以是文件也可以是文件夹File[] fileList file.listFiles();//将该目录下的…...
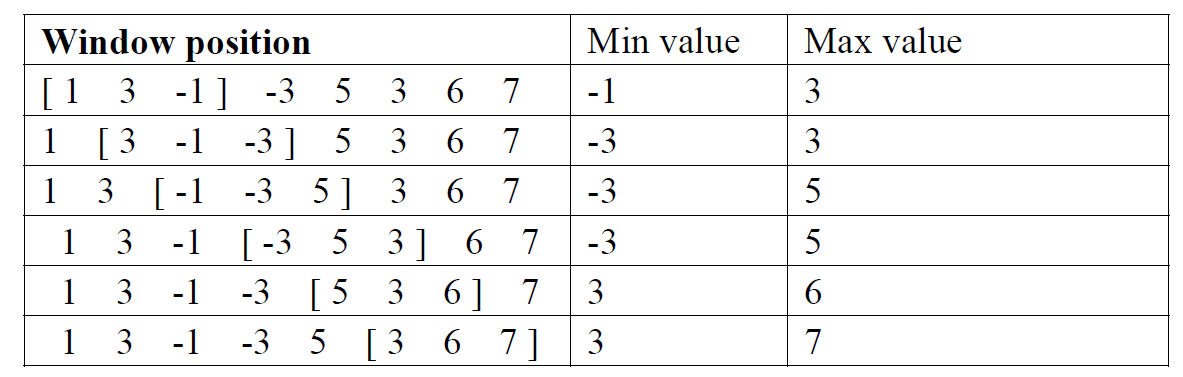
Window问题详解(下)
建议先看一下 Window问题详解(上) 思路② 既然会超时,那该怎么办呢? 显然需要一个更快速的方法来解决这个问题! 我们先来观察一下图片: 我们发现,每一次选中的数都会增加下一个。 !!!!! 因此,我们可以根据此特性优化时间!! 第一次先求出前 k − 1 k-1 k−...

Kafka部署与SpringBoot集成
Kafka与ZooKeeper Apache ZooKeeper是一个基于观察者模式的分布式服务管理框架,即服务注册中心。同时ZooKeeper还具有存储数据的能力。Kafka的每台服务器作为一个broker注册到ZooKeeper,多个broker借助ZooKeeper形成了Kafka集群。同时ZooKeeper会保存一…...
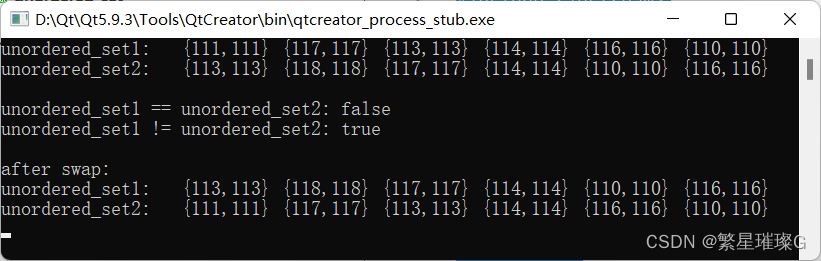
c++11 标准模板(STL)(std::unordered_set)(十三)
定义于头文件 <unordered_set> template< class Key, class Hash std::hash<Key>, class KeyEqual std::equal_to<Key>, class Allocator std::allocator<Key> > class unordered_set;(1)(C11 起)namespace pmr { templ…...

【2023】DevOps、SRE、运维开发面试宝典之ELKStack相关面试题
文章目录 1、elasticsearch的应用场景2、elasticsearch的特点3、Elasticsearch集群三种状态分别是什么?代表什么?4、Elasticsearch集群的优化方面5、Elasticsearch集群防止脑裂的配置参数?6、ELK日志采集平台架构组件介绍?7、Logstash组件的作用?8、收集Kubernetes集群程序…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

