数字逻辑基础:原码、反码、补码
时间紧、不理解可以只看这里的结论
正数的原码、反码、补码相同。等于真值对应的机器码。
负数的原码等于机器码,反码为原码的符号位不变,其余各位按位取反。补码为反码+1。
三种码的出现是为了解决计算问题并简化电路结构。
在原码和反码中,存在正零+0和负零-0。
补码的出现用到了模的知识。
机器数和真值
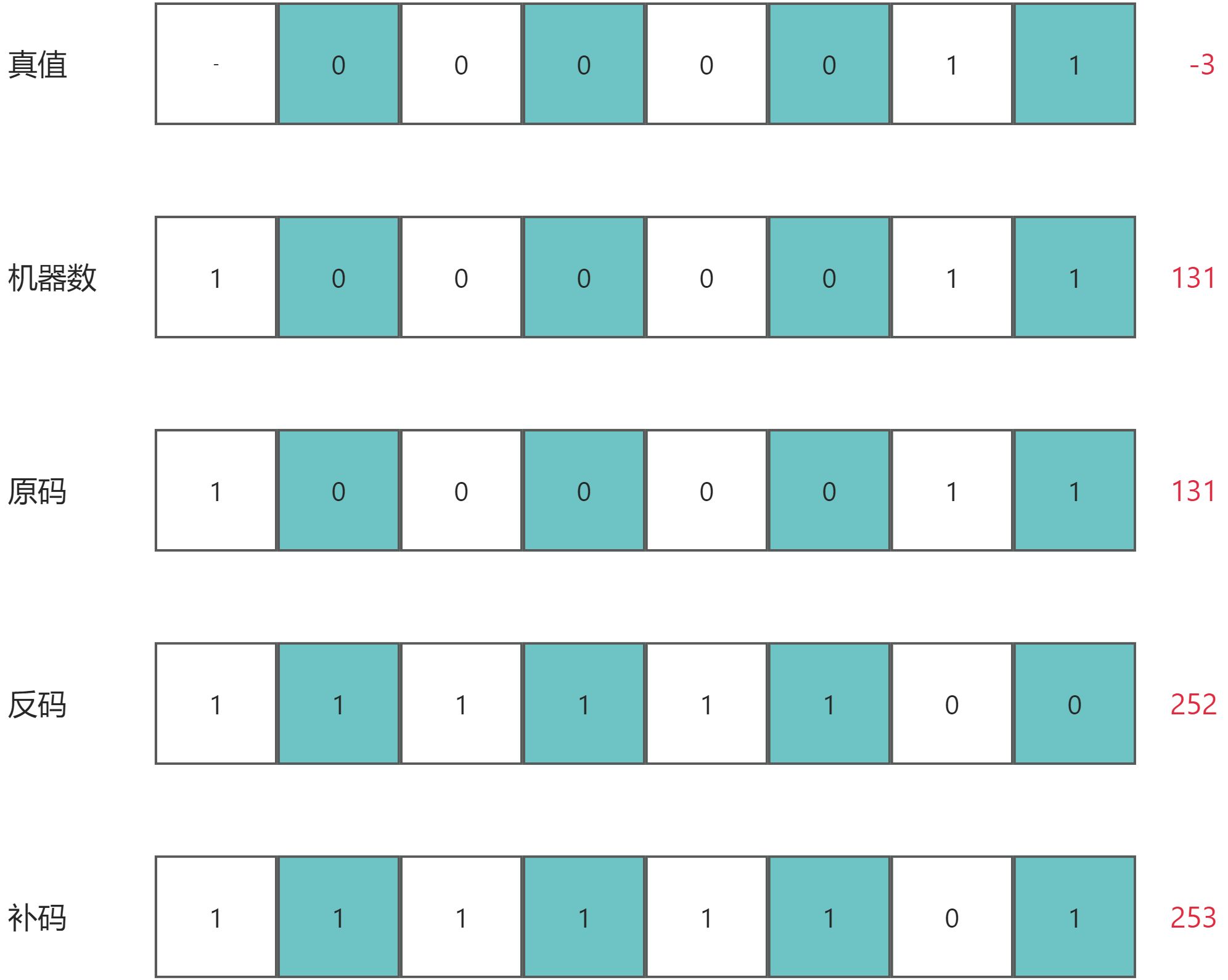
日常书写时在数值前面用+号表示正数,-号表示负数,这种带符号的二进制数称为真值。
计算机处理时,必须将+和-转换为数码,符号数码化的数被称为机器数。
一般将符号位放到最高位,用0表示正,用1表示负。
机器数
以3为例,+3对应的二进制数是00000011,-3对应的二进制数是10000011。
二进制数00000011和10000011就是机器数。
真值
因为第一位是符号位,所以机器数的形式值就不等于真正的数值。
例如上面的有符号数10000011,其最高位1代表负,其真正数值是-3而不是形式值131(10000011转换成十进制等于131)。所以,为区别起见,将带符号位的机器数对应的真正数值称为机器数的真值。
如:0000 0011的真值 = +000 0011,1000 0011的真值 =–000 0011
原码
原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值. 比如如果是8位二进制:
[+1]原 = 0000 0001
[-1]原 = 1000 0001
因为第一位是符号位, 所以8位二进制数的取值范围就是:[1111 1111 , 0111 1111],即[-127 , 127]。
原码是人脑最容易理解和计算的表示方式。
以"3+3"、"3+(-3)"、"-3+(-3)"为例,如果使用传统的加减法规则,逢二进一:
0000 0011+0000 0011=0000 0110=6,结果正确。0000 0011+1000 0011=1000 0110=-6,结果错误。1000 0011+1000 0011=10000 0110=-6,数据溢出。
在计算正数时,使用原码可以正常运算,但如果出现负数或减法运算,则会出错。
因此,原码在计算时,有着一套额外的规则。
原码的加法规则:
- 判断被加数和加数的符号是同号还是异号。
- 同号时,做加法,结果的符号就是被加数的符号。
- 异号时,先比较被加数和加数的数值(绝对值)大小,然后由大值减去小值,结果的符号取大值的符号。
由于原码运算规则复杂,为了简化机器数的运算,因此需要寻找其他表示负数的方法,即之后的反码和补码。
反码
正数的反码是其本身。
负数的反码是在其原码的基础上, 符号位不变,其余各位按位取反。
也叫真值的按位变反。
[+1] = [00000001]原 = [00000001]反
[-1] = [10000001]原 = [11111110]反
可见如果一个反码表示的是负数, 人脑无法直观的看出来它的数值. 通常要将其转换成原码再计算。
补码
补码的表示方法是:
- 正数的补码就是其本身。
- 负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1。
[+1] = [00000001]原 = [00000001]反 = [00000001]补
[-1] = [10000001]原 = [11111110]反 = [11111111]补
对于负数, 补码表示方式也是人脑无法直观看出其数值的. 通常也需要转换成原码在计算其数值。
为什么要有三种码
首先,因为人脑可以知道第一位是符号位,在计算的时候我们会根据符号位,选择对真值区域的加减 (真值的概念在本文最开头)。
但是对于计算机,加减乘数已经是最基础的运算,要设计的尽量简单。
计算机辨别"符号位"显然会让计算机的基础电路设计变得十分复杂。
于是人们想出了将符号位也参与运算的方法。
我们知道,根据运算法则减去一个正数等于加上一个负数,即,1-1 = 1 + (-1) = 0,所以机器可以只有加法而没有减法,这样计算机运算的设计就更简单了。
如果用原码表示,让符号位也参与计算,显然对于减法来说,结果是不正确的。
这也就是为何计算机内部不使用原码表示一个数。
计算十进制的表达式: 1-1=0
1 - 1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原= [0000 0001]反 + [1111 1110]反 = [1111 1111]反 = [1000 0000]原 = -0
发现用反码计算减法,结果的真值部分是正确的。
而唯一的问题其实就出现在"0"这个特殊的数值上。虽然人们理解上+0和-0是一样的。但是0带符号是没有任何意义的。而且会有[0000 0000]原和[1000 0000]原两个编码表示0。
于是补码的出现, 解决了0的符号以及两个编码的问题
1-1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原 = [0000 0001]补 + [1111 1111]补 = [0000 0000]补=[0000 0000]原
这样0用[0000 0000]表示, 而以前出现问题的-0则不存在了.而且可以用[1000 0000]表示-128:
(-1) + (-127) = [1000 0001]原 + [1111 1111]原 = [1111 1111]补 + [1000 0001]补 = [1000 0000]补
-1-127的结果应该是-128, 在用补码运算的结果中, [1000 0000]补就是-128。 但是注意因为实际上是使用以前的-0的补码来表示-128,所以-128并没有原码和反码表示。(对-128的补码表示[1000 0000]补算出来的原码是[0000 0000]原, 这是不正确的)。
- 整数0的补码只有一种形式,即
00000000。 - 补码
10000000表示-128。
使用补码,不仅仅修复了0的符号以及存在两个编码的问题,而且还能够多表示一个最低数。这就是为什么8位二进制,使用原码或反码表示的范围为[-127, +127],而使用补码表示的范围为[-128, 127]。
因为机器使用补码, 所以对于编程中常用到的32位int类型, 可以表示范围是:[-2^31, 2^31-1],因为第一位表示的是符号位,而使用补码表示时又可以多保存一个最小值。
当真值用补码表示时,补码加法的规律和无符号数的加法规律完全一样,因此简化了加法器的设计。
运算时符号位和数值位一起参加运算,不必处理符号位上的进位,即丢弃符号位上的进位。
模%mod的应用
推荐一位博客园的大佬
https://www.cnblogs.com/zhangziqiu/archive/2011/03/30/computercode.html
计算机巧妙地把符号位参与运算,并且将减法变成了加法,背后蕴含了怎样的数学原理呢?
将钟表想象成是一个1位的12进制数。
如果当前时间是6点,我希望将时间设置成4点,我们可以:
- 往回拨2个小时: 6 - 2 = 4
- 往前拨10个小时: (6 + 10) mod 12 = 4
- 往前拨10+12=22个小时: (6+22) mod 12 =4
所以钟表往回拨(减法)的结果可以用往前拨(加法)替代。
现在的焦点就落在了如何用一个正数,来替代一个负数。
同余的概念
两个整数a,b,若它们除以整数m所得的余数相等,则称a,b对于模m同余。
记作a ≡ b (mod m)。
读作 a 与 b 关于模 m 同余。
举例说明:
- 4 mod 12 = 4
- 16 mod 12 = 4
- 28 mod 12 = 4
所以4, 16, 28关于模 12 同余。
线性运算定理:
如果a ≡ b (mod m),c ≡ d (mod m) 那么:
a ± c ≡ b ± d (mod m)a * c ≡ b * d (mod m)
-1的反码表示是1111 1110. 如果这里将[1111 1110]认为是原码, 则[1111 1110]原 = -126, 这里将符号位除去, 即认为是126。
发现有如下规律:
(-1) mod 127 = 126126 mod 127 = 126
即:
(-1) ≡ 126 (mod 127)2-1 ≡ 2+126 (mod 127)
2-1 与 2+126的余数结果是相同的! 而这个余数, 正式我们的期望的计算结果: 2-1=1
所以说一个数的反码,实际上是这个数对于一个膜的同余数。而这个膜并不是我们的二进制,而是所能表示的最大值。这就和钟表一样,转了一圈后总能找到在可表示范围内的一个正确的数值。
而2+126很显然相当于钟表转过了一轮,而因为符号位是参与计算的,正好和溢出的最高位形成正确的运算结果。
既然反码可以将减法变成加法, 那么现在计算机使用的补码呢? 为什么在反码的基础上加1, 还能得到正确的结果?
2-1=2+(-1) = [0000 0010]原 + [1000 0001]原 = [0000 0010]补 + [1111 1111]补
如果把[1111 1111]当成原码, 去除符号位, 则:
[0111 1111]原 = 127
其实, 在反码的基础上+1, 只是相当于增加了膜的值:
(-1) mod 128 = 127127 mod 128 = 1272-1 ≡ 2+127 (mod 128)
此时, 表盘相当于每128个刻度转一轮. 所以用补码表示的运算结果最小值和最大值应该是[-128, 128]。
但是由于0的特殊情况, 没有办法表示128, 所以补码的取值范围是[-128, 127]。
相关文章:

数字逻辑基础:原码、反码、补码
时间紧、不理解可以只看这里的结论 正数的原码、反码、补码相同。等于真值对应的机器码。 负数的原码等于机器码,反码为原码的符号位不变,其余各位按位取反。补码为反码1。 三种码的出现是为了解决计算问题并简化电路结构。 在原码和反码中,存…...

有限差分法-差商公式及其Matlab实现
2.1 有限差分法 有限差分法 (finite difference method)是一种数值求解偏微分方程的方法,它将偏微分方程中的连续变量离散化为有限个点上的函数值,然后利用差分逼近导数,从而得到一个差分方程组。通过求解差分方程组,可以得到原偏微分方程的数值解。 有限差分法是一种历史…...

高校就业信息管理系统
1引言 1.1编写目的 1.2背景 1.3定义 1.4参考资料 2程序系统的结构 3登录模块设计说明一 3.1程序描述 3.2功能 3.3性能 3.4输人项 3.5输出项 3.6算法 3.7流程逻辑 3.8接口 3.10注释设计 3.11限制条件 3.12测试计划 3.13尚未解决的问题 4注册模块设计说明 4.…...

【Java|golang】2373. 矩阵中的局部最大值
给你一个大小为 n x n 的整数矩阵 grid 。 生成一个大小为 (n - 2) x (n - 2) 的整数矩阵 maxLocal ,并满足: maxLocal[i][j] 等于 grid 中以 i 1 行和 j 1 列为中心的 3 x 3 矩阵中的 最大值 。 换句话说,我们希望找出 grid 中每个 3 x …...
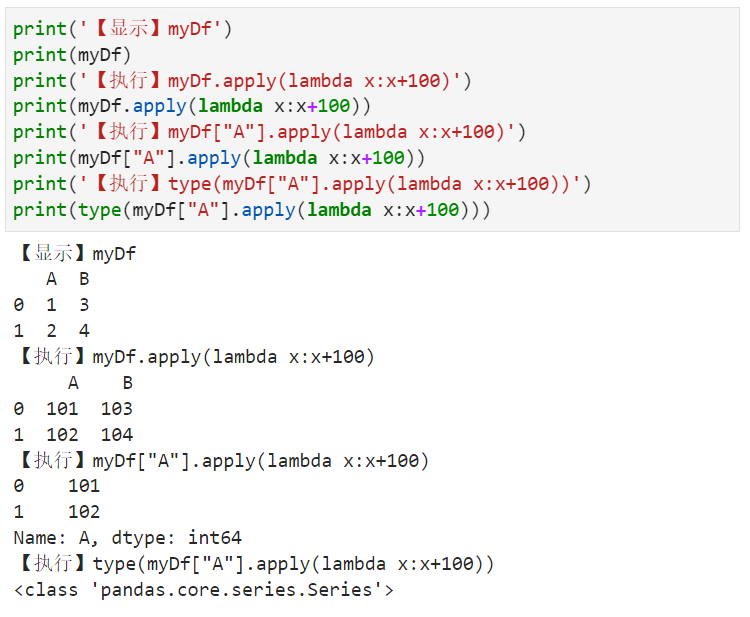
根据指定函数对DataFrame中各元素进行计算
【小白从小学Python、C、Java】【计算机等级考试500强双证书】【Python-数据分析】根据指定函数对DataFrame中各元素进行计算以下错误的一项是?import numpy as npimport pandas as pdmyDict{A:[1,2],B:[3,4]}myDfpd.DataFrame(myDict)print(【显示】myDf)print(myDf)print(【…...

【蓝桥杯集训·每日一题】AcWing 3502. 不同路径数
文章目录一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解三、知识风暴一、题目 1、原题链接 3502. 不同路径数 2、题目描述 给定一个 nm 的二维矩阵,其中的每个元素都是一个 [1,9] 之间的正整数。 从矩阵中的任意位置出发…...
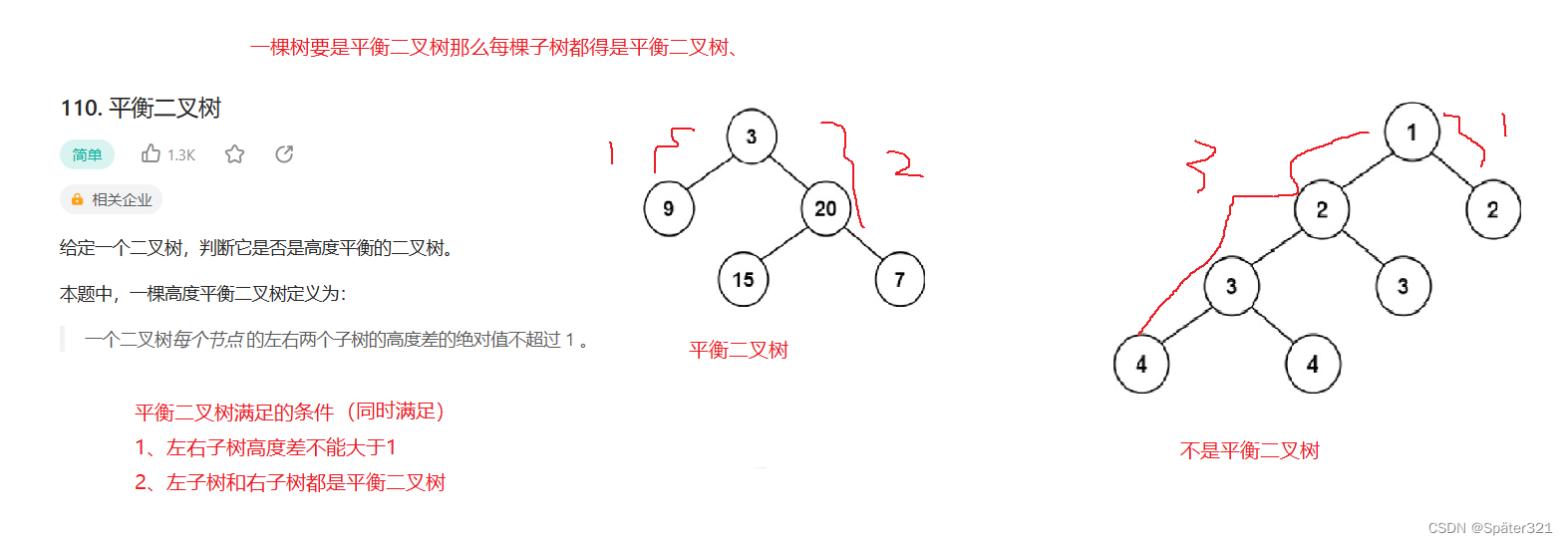
Java - 数据结构,二叉树
一、什么是树 概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点: 1、有…...
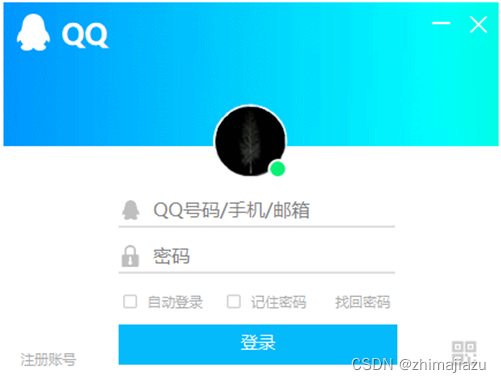
模拟QQ登录-课后程序(JAVA基础案例教程-黑马程序员编著-第十一章-课后作业)
【案例11-3】 模拟QQ登录 【案例介绍】 1.案例描述 QQ是现实生活中常用的聊天工具,QQ登录界面看似小巧、简单,但其中涉及的内容却很多,对于初学者练习Java Swing工具的使用非常合适。本案例要求使用所学的Java Swing知识,模拟实…...
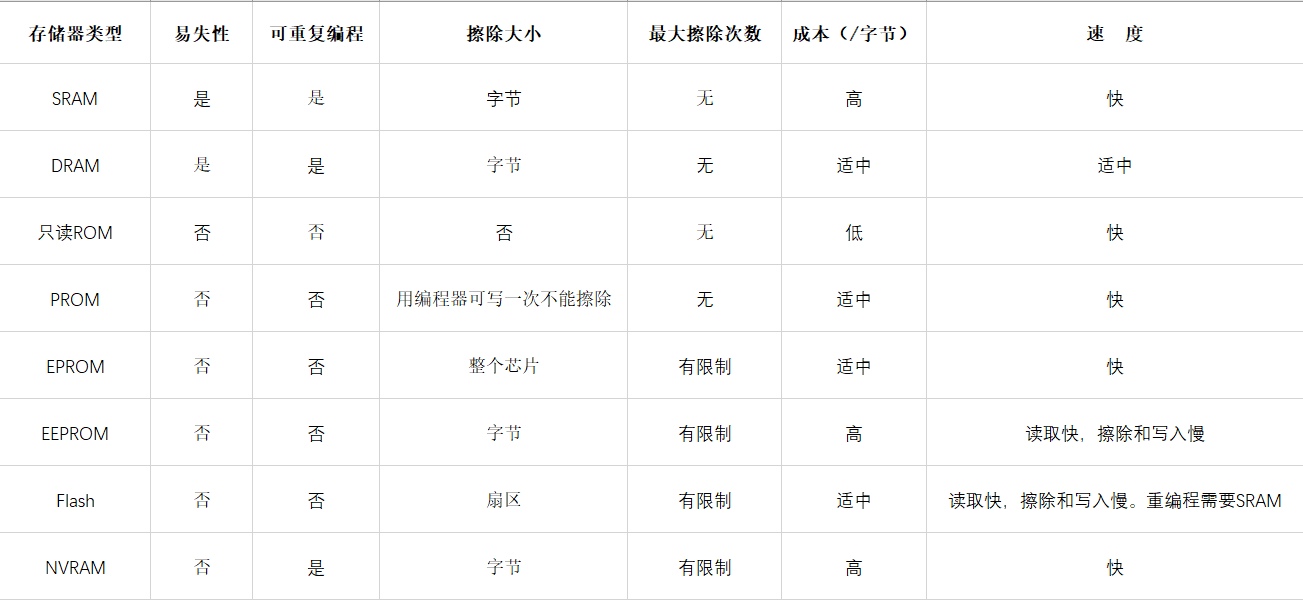
【壹】嵌入式系统硬件基础
随手拍拍💁♂️📷 日期: 2023.2.28 地点: 杭州 介绍: 日子像旋转毒马🐎,在脑海里转不停🤯 🌲🌲🌲🌲🌲 往期回顾 🌲🌲🌲…...
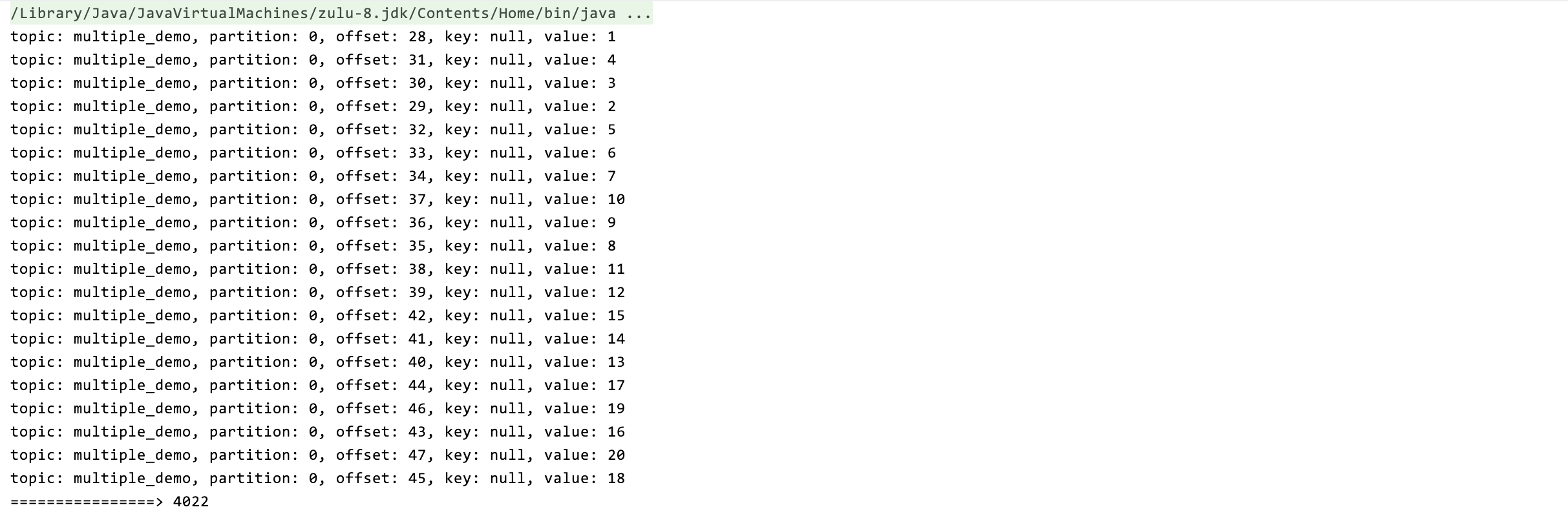
当参数调优无法解决kafka消息积压时可以这么做
今天的议题是:如何快速处理kafka的消息积压 通常的做法有以下几种: 增加消费者数增加 topic 的分区数,从而进一步增加消费者数调整消费者参数,如max.poll.records增加硬件资源 常规手段不是本文的讨论重点或者当上面的手段已经使…...
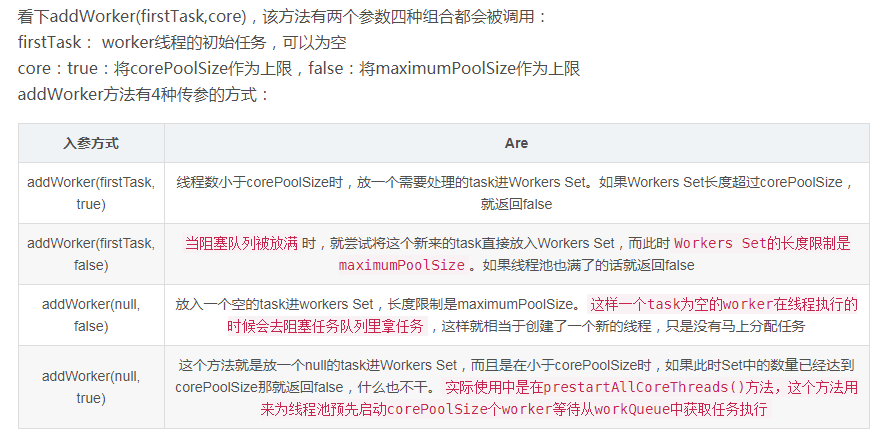
Java线程池源码分析
Java 线程池的使用,是面试必问的。下面我们来从使用到源码整理一下。 1、构造线程池 通过Executors来构造线程池 1、构造一个固定线程数目的线程池,配置的corePoolSize与maximumPoolSize大小相同, 同时使用了一个无界LinkedBlockingQueue存…...
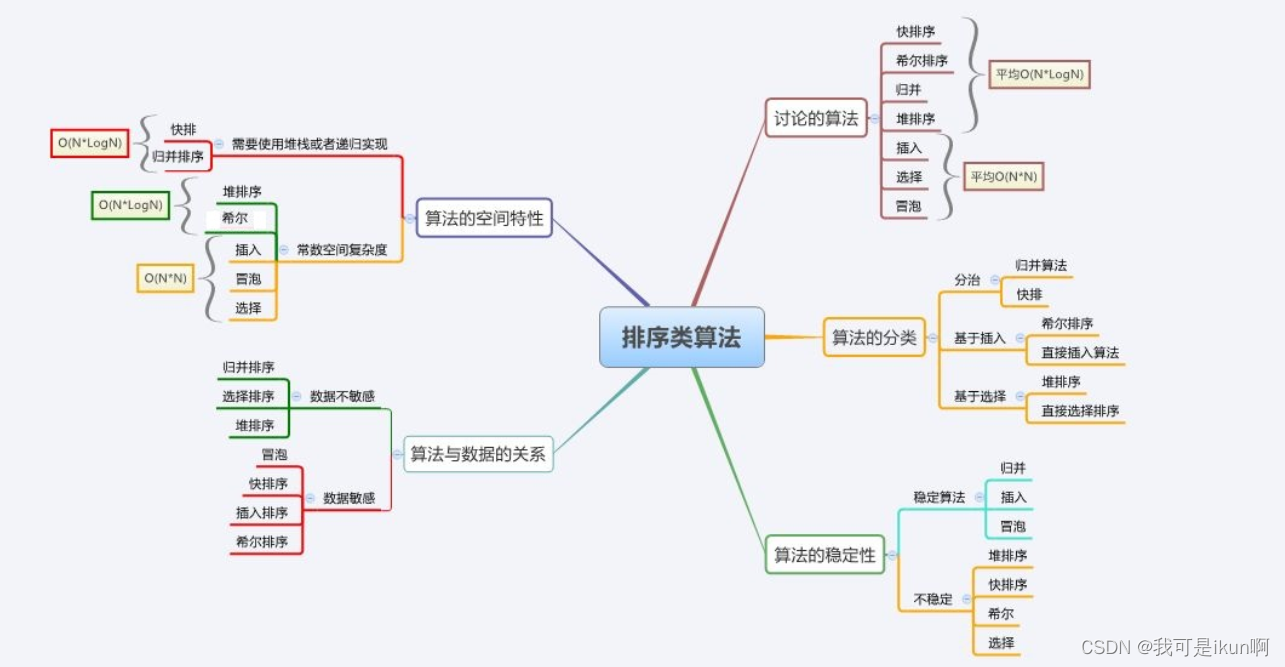
手撕八大排序(下)
目录 交换排序 冒泡排序: 快速排序 Hoare法 挖坑法 前后指针法【了解即可】 优化 再次优化(插入排序) 迭代法 其他排序 归并排序 计数排序 排序总结 结束了上半章四个较为简单的排序,接下来的难度将会大幅度上升&…...
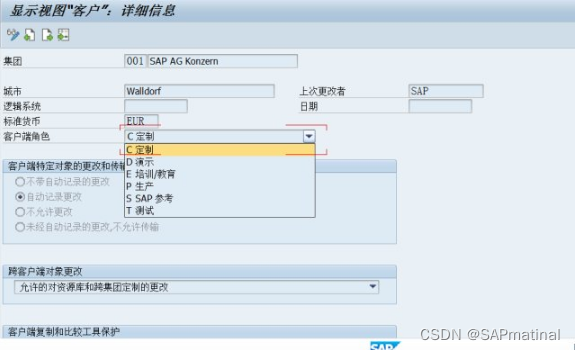
SAP 详细解析SCC4
事务代码:SCC4,选择一个客户端,点击进入,如图: 一、客户端角色 客户控制:客户的角色(生产性,测试,...) 此属性表示 R/3 系统中的客户端角色。其中可能包括…...
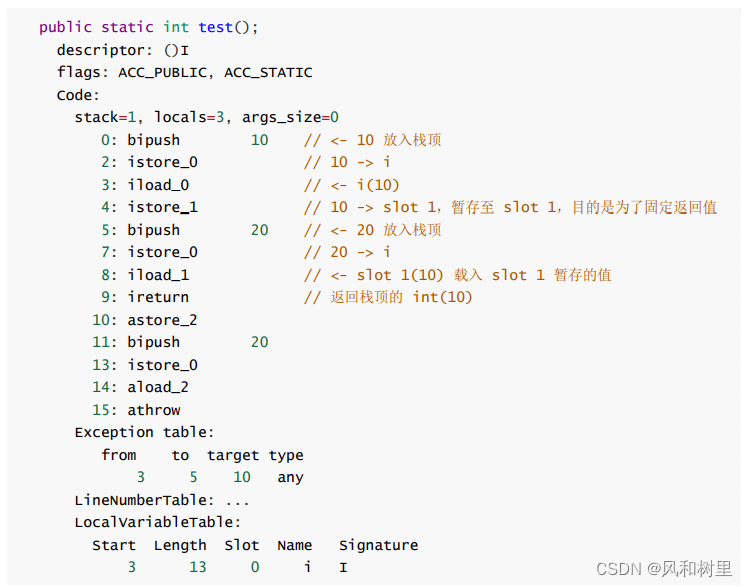
java异常分类和finally代码块中return语句的影响
首先看一下java中异常相关类的继承关系: 引用 1、分类 异常可以分为受查异常和非受查异常,Error和RuntimeException及其所有的子类都是非受查异常,其他的是受查异常。 两者的区别主要在: 受检的异常是由编译器(编译…...

【链表OJ题(二)】链表的中间节点
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:数据结构 🎯长路漫漫浩浩,万事皆有期待 文章目录链表OJ题(二)1. 链表…...
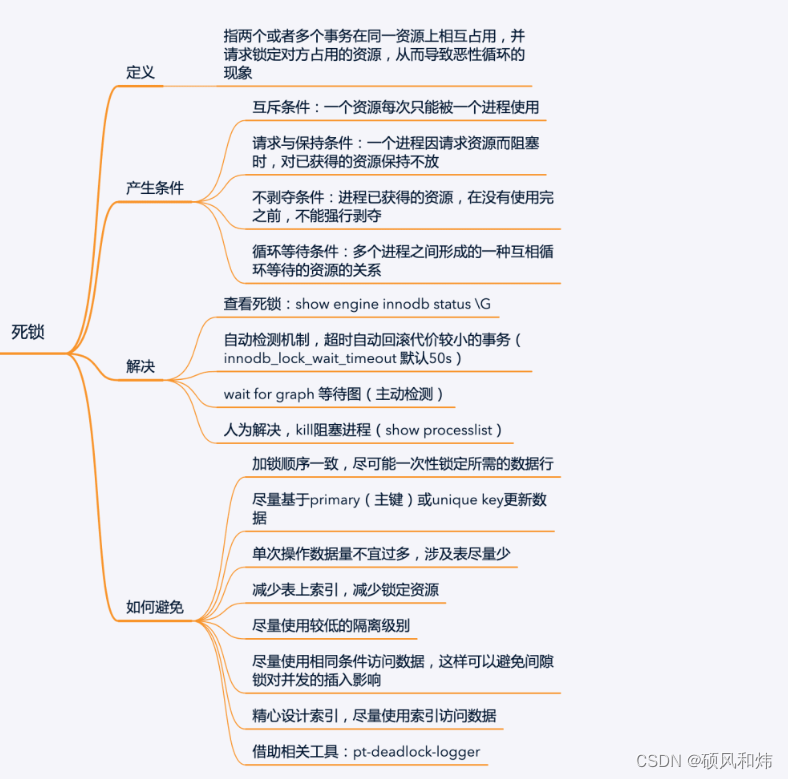
【强烈建议收藏:MySQL面试必问系列之并发事务锁专题】
一.知识回顾 上节课我们一起学习了MySQL面试必问系列之事务,没有学习的同学可以看一下上一篇文章,肯定对你会有帮助,学习过的同学肯定知道,上节课我们留了一个小尾巴,这个小尾巴是什么呢?就是没有详细展开…...
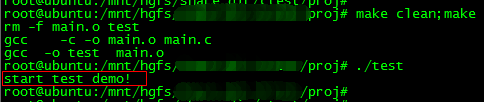
Linux下使用Makefile实现条件编译
在Linux系统下Makefile和C/C语言都有提供条件选择编译的语法,就是在编译源码的时候,可以选择性地编译指定的代码。这种条件选择编译的使用场合有好多,例如我们开发一个兼容标准版本与定制版本兼容的项目,那么,一些与需…...
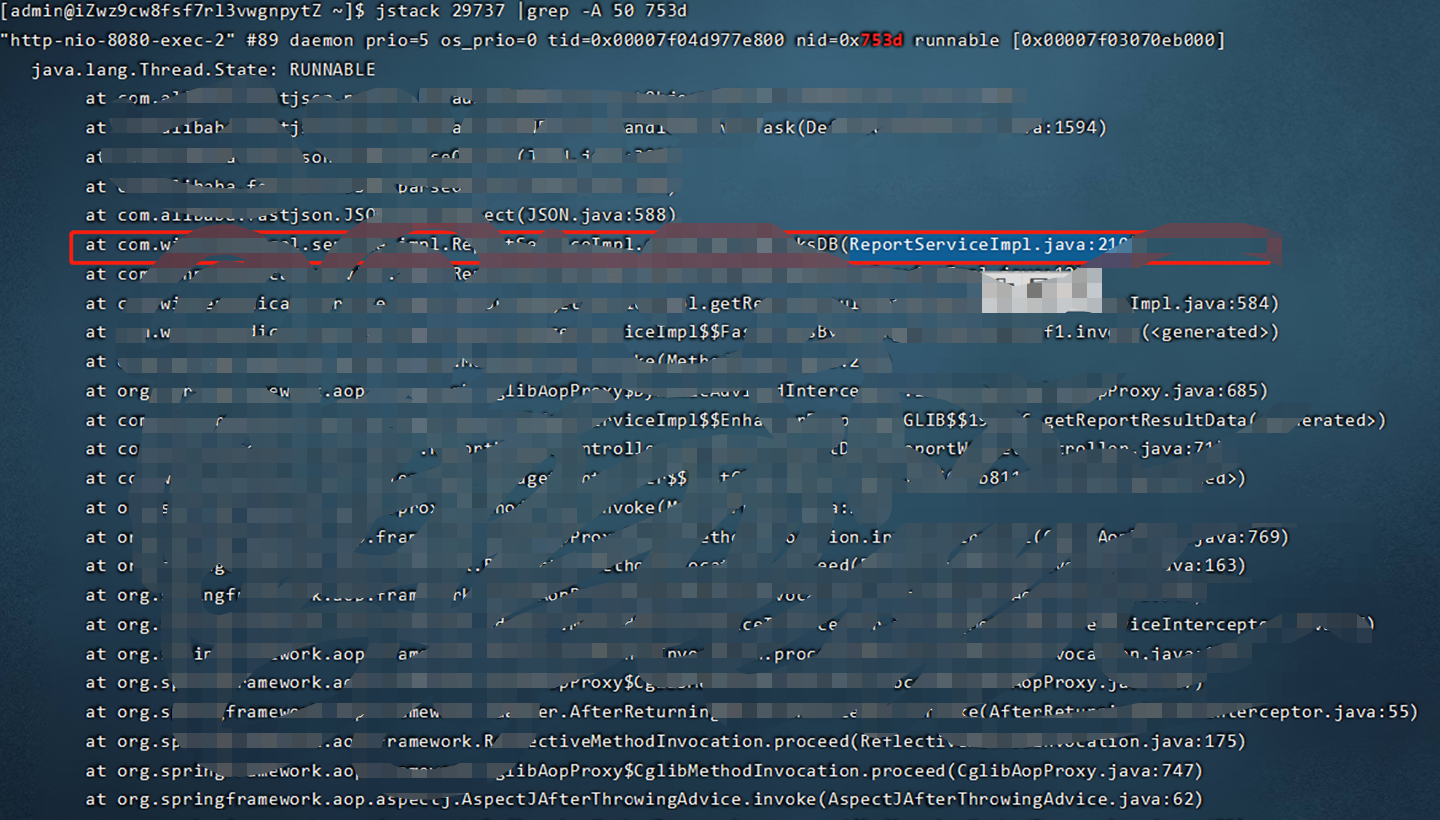
java 应用cpu飙升(超过100%)故障排查
前言害。。。昨天刚写完一份关于jvm问题排查相关的博客,今天线上项目就遇到了一个突发问题。现象是用户反映系统非常卡,无法操作。然后登录服务器查看发现cpu 一直100%以上。具体排查步骤:1,首先top命令查看服务器cpu等情况&#…...
光学设计软件Ansys的Lumerical 2023版本下载与安装使用
文章目录前言一、许可管理工具安装二、许可管理器配置三、Lumerical安装四、工具使用配置总结前言 Lumerical是一款功能强大的软件,用于设计和分析从组件到系统阶段的光子学和电磁学。这个版本的Lumerical改进了电子和光子学设计工具,用于复杂光子学&am…...
Java 异常
文章目录1. 异常概述2. JVM 的默认处理方案3. 异常处理之 try...catch4. Throwable 的成员方法5. 编译异常和运行异常的区别6. 异常处理之 throws7. 自定义异常8. throws 和 throw 的区别1. 异常概述 异常就是程序出现了不正常的情况。 ① Error:严重问题ÿ…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...
