【数据结构高阶】红黑树
目录
一、红黑树的概念
二、红黑树的性质
2.1 红黑树与AVL树的比较
三、红黑树的实现
3.1 红黑树节点的定义
3.2 数据的插入
3.2.1 红黑树的调整思路
3.2.1.1 cur为红,f为红,g为黑,u存在且为红
3.2.1.2 cur为红,f为红,g为黑,u不存在/u存在且为黑
3.2.1.2.1 g、f、cur构成一条直线
3.2.1.2.2 g、f、cur构成一条折线
3.2.2 调整部分的代码实现
3.3 红黑树的验证
3.4 测试代码
四、红黑树实现完整代码
一、红黑树的概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路 径会比其他路径长出俩倍,因而是接近平衡的。
二、红黑树的性质
● 每个结点不是红色就是黑色
● 根节点是黑色的
● 如果一个节点是红色的,则它的两个孩子结点是黑色的(不允许出现连续的红色节点)
● 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点(从根节点到每个叶子节点的空孩子路径上有相同数目的黑色节点)
● 每个叶子结点的空孩子节点都是黑色的
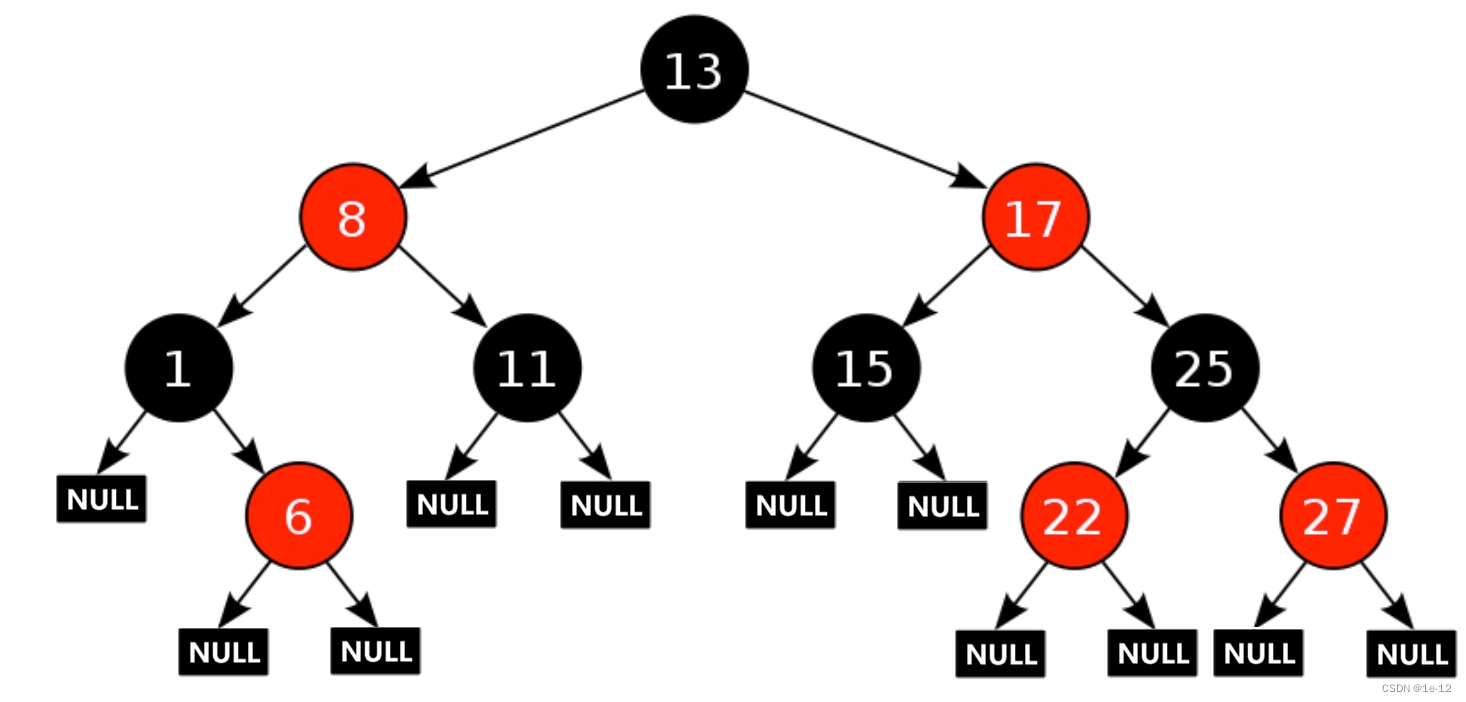
根据上述的五条性质,我们可以发现一个红黑树中如果有N个黑色节点,则根节点到任意一个叶子节点的距离:最短为㏒⑵N,最长为2㏒⑵N
2.1 红黑树与AVL树的比较
我们来看到下面的红黑树:
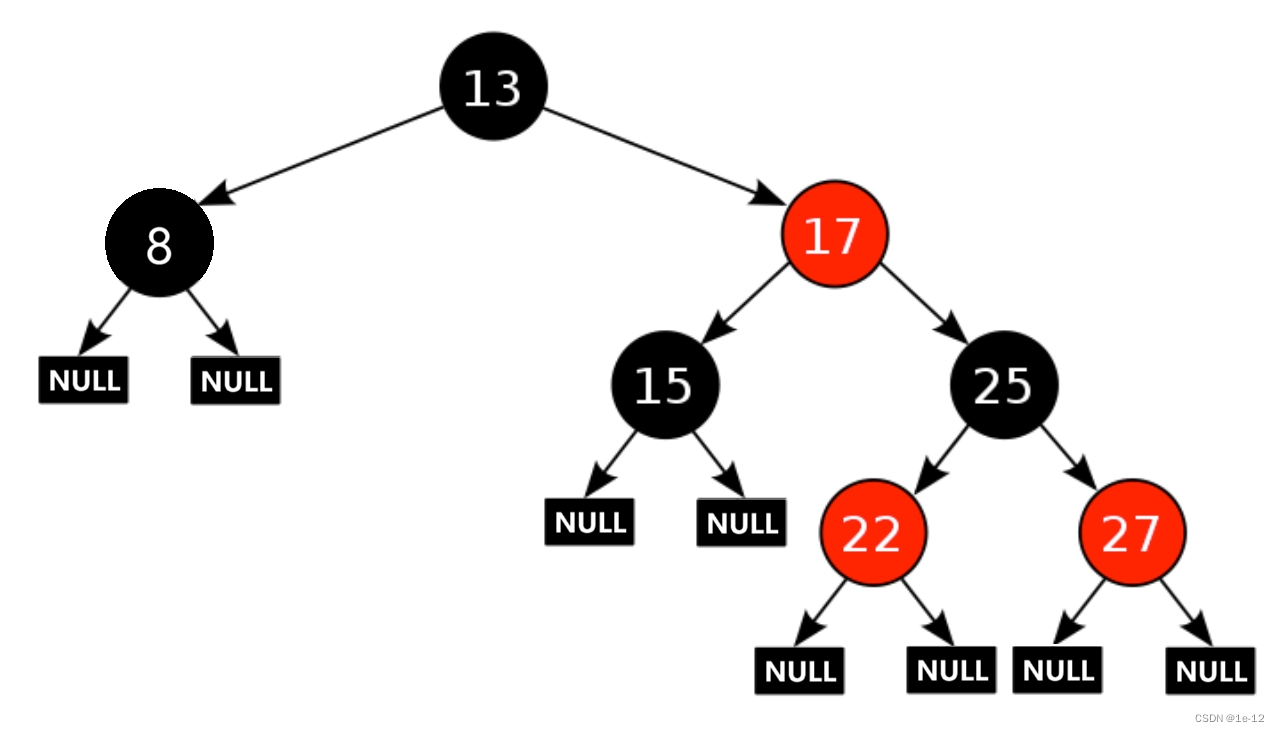
对于这棵红黑树,如果将其看成一个AVL树,是需要进行旋转的,但是在红黑树结构中却不需要
所以红黑树是近似平衡的,在搜索效率上会略逊AVL树一些,但是红黑树在结构上不要求绝对的平衡,这就造成插入相同的数据红黑树翻转的次数少于AVL树
实际使用中,在经常进行增删的场景下红黑树性能比AVL树更优,并且红黑树实现比较简单,所以实际运用中红黑树更多
三、红黑树的实现
3.1 红黑树节点的定义
enum Colour
{RED,BLACK
};template<class Key, class Val>
struct RBTreeNode
{RBTreeNode<Key, Val>* _left;RBTreeNode<Key, Val>* _right;RBTreeNode<Key, Val>* _parent;//多一个指针指向其父节点,方便我们的后续操作pair<Key, Val> _kv;Colour _col;//颜色标识RBTreeNode(const pair<Key, Val>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_col(RED)//构造时,优先将节点的颜色置为红色{}
};
在这里提一下为什么要默认将节点的颜色置为红色:
在我们向红黑树中插入一个新节点时,如果将该节点置为黑色,就肯定会影响红黑树性质中的第四条:对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点
例如:
我们现在在上面这棵树中,不管在哪个叶子节点的下方插入一个黑色的新增节点,从根节点到插入的节点的空孩子的路径上的黑色节点数目会变为4,而从根节点到其他叶子节点的空孩子的路径上的黑色节点数目会都为3
所以我们将新增节点的颜色置为红色就一定不会违反第四条红黑树性质,但是第三条呢?如果插入节点的父节点是红色的怎么办?
怎么办我们后面再说,反正总归比置为黑色一定会违反第四条性质好吧
3.2 数据的插入
由于红黑树也是平衡二叉搜索树的一种,我们在插入数据时也要找到合适的位置进行插入:
template<class Key, class Val>
class RBTree
{typedef RBTreeNode<Key, Val> Node;
public:bool Insert(const pair<Key,Val>& kv){Node* cur = _root, * parent = nullptr;while (cur)//找到合适的位置{if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else{cout << "插入的值重复" << endl;return false;}}cur = new Node(kv);cur->_parent = parent;//将插入的节点连接上二叉树if (parent == nullptr){_root = cur;}else if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}return true;}private:Node* _root = nullptr;
};
插入到合适的位置之后,我们还要检查是否破坏了红黑树的结构(由于我们插入的是红色节点,所以只会出现两个红色节点连续的情况),如果出现了该情况,我们就要对其进行分类讨论并解决:
3.2.1 红黑树的调整思路
下面我们将出现异常情况的两个节点的那个子节点叫做cur,cur的父节点叫做father(简称f),father的父节点叫做grandfather(简称g),father的兄弟节点叫做uncle(简称u)
例如: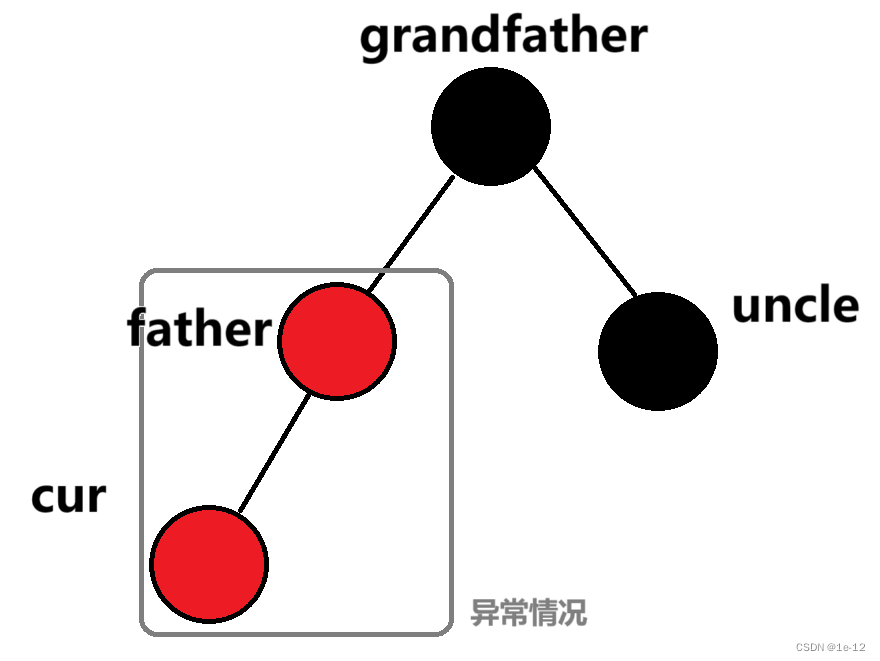
接下来,我们分类讨论:
3.2.1.1 cur为红,f为红,g为黑,u存在且为红
下面画出的情况表示的是抽象出的情况:A、B、C、D、E都是满足构成红黑树的子树
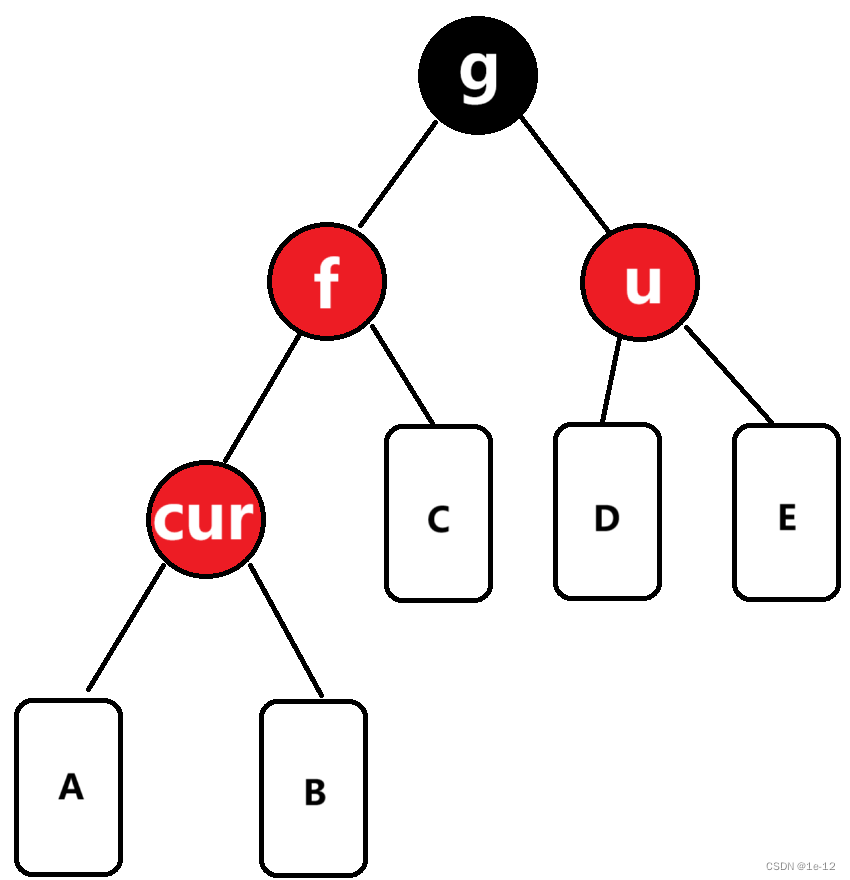
对于这种情况我们先将f和u节点变黑,再将g节点变红即可:
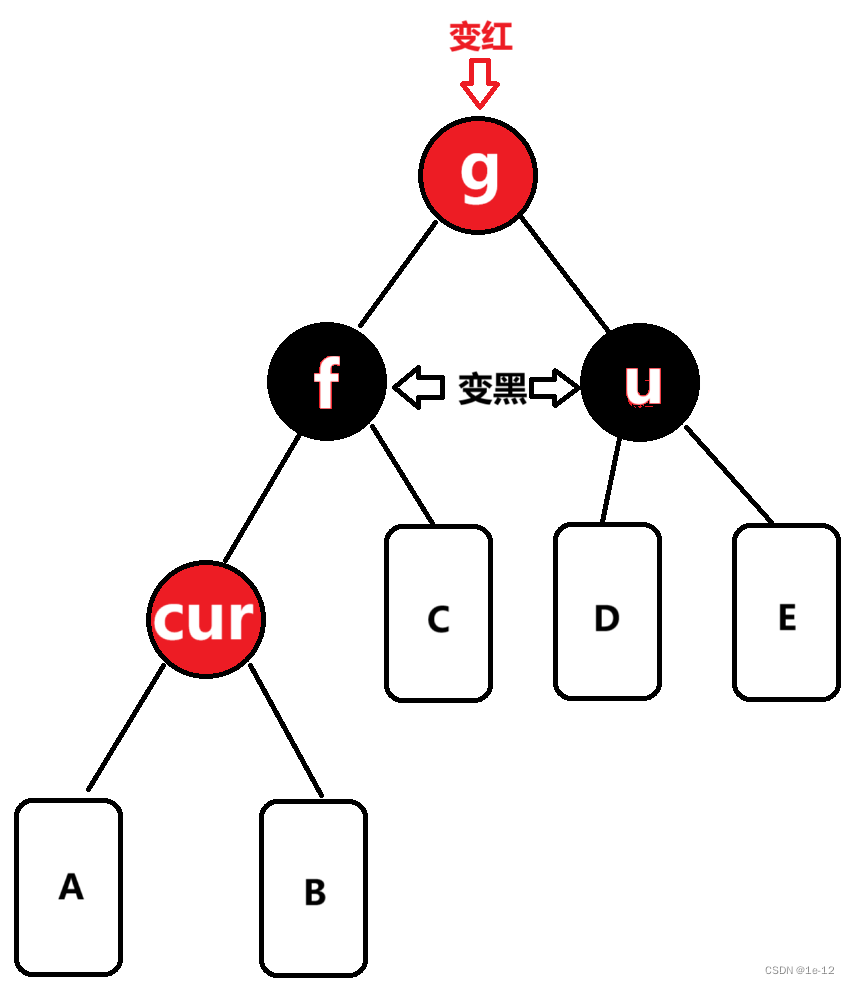
调整完后,要记得再向上检查g节点的父节点是否为红色哦~(如果g节点为整棵红黑树的根,最后要将其颜色置为黑)
3.2.1.2 cur为红,f为红,g为黑,u不存在/u存在且为黑
3.2.1.2.1 g、f、cur构成一条直线
对于这种情况:若f为g的左孩子,cur为f的左孩子,则进行右单旋:

再将f变黑,g变红:
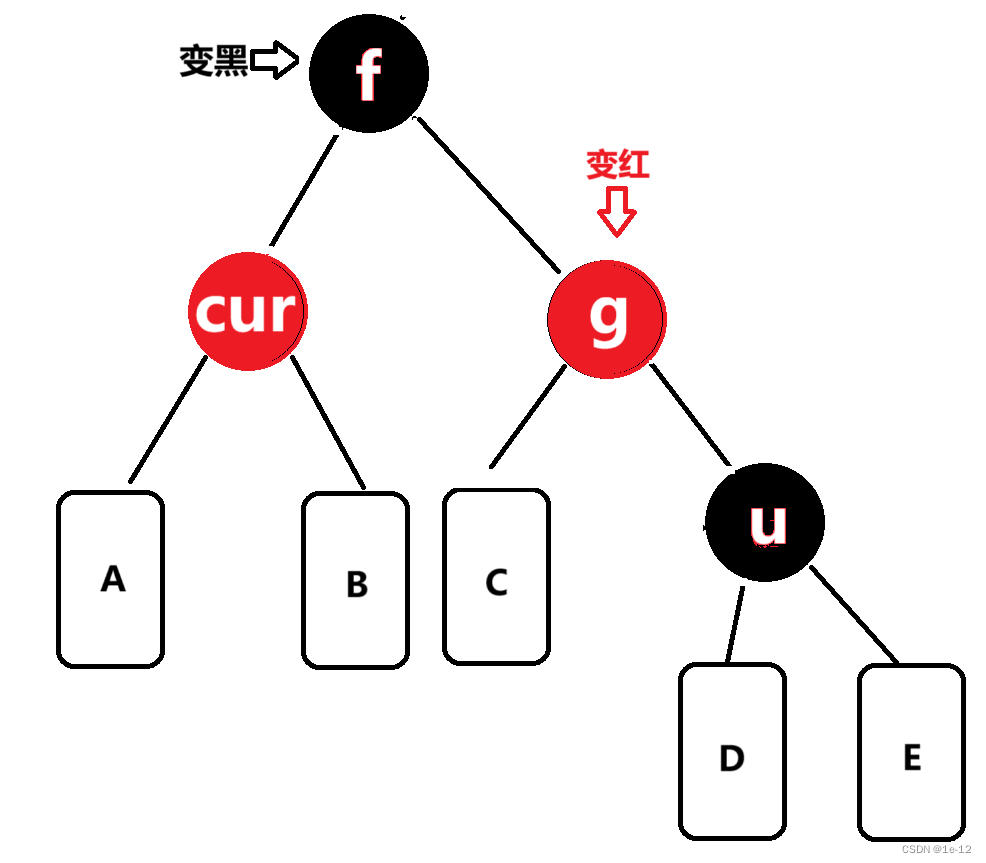
相反, f为g的右孩子,cur为f的右孩子,则进行左单旋转:
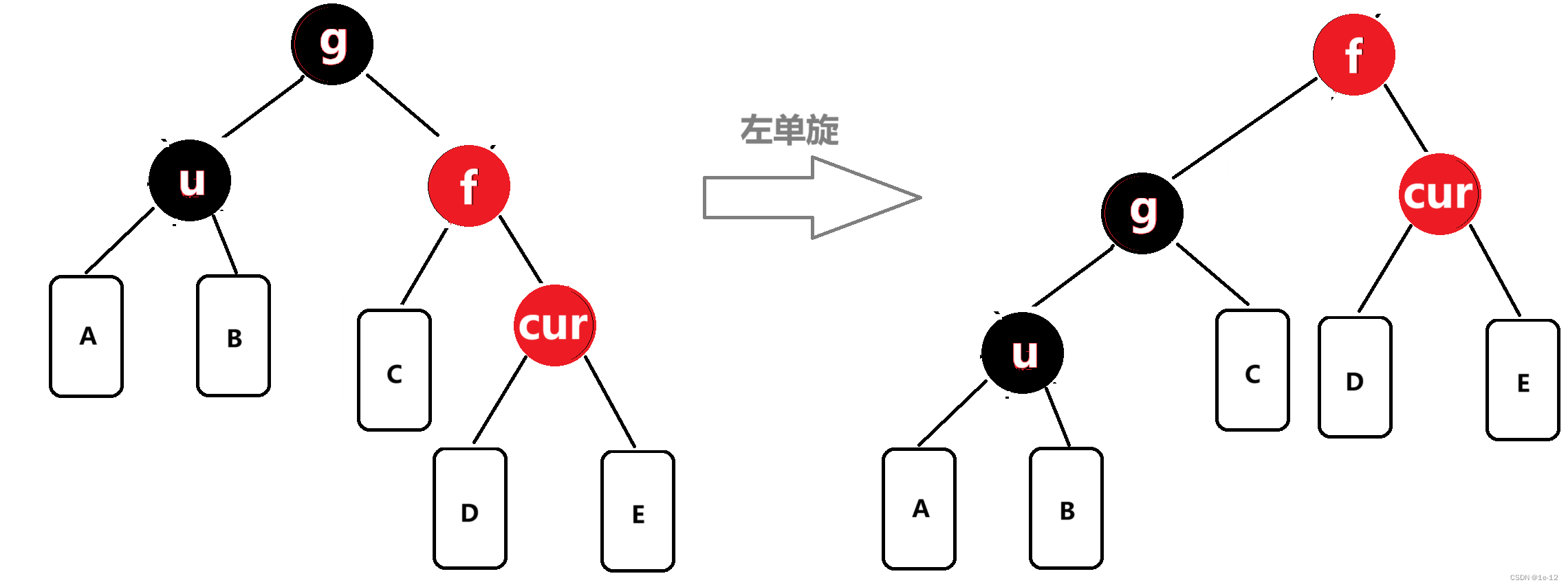
再将f变黑,g变红: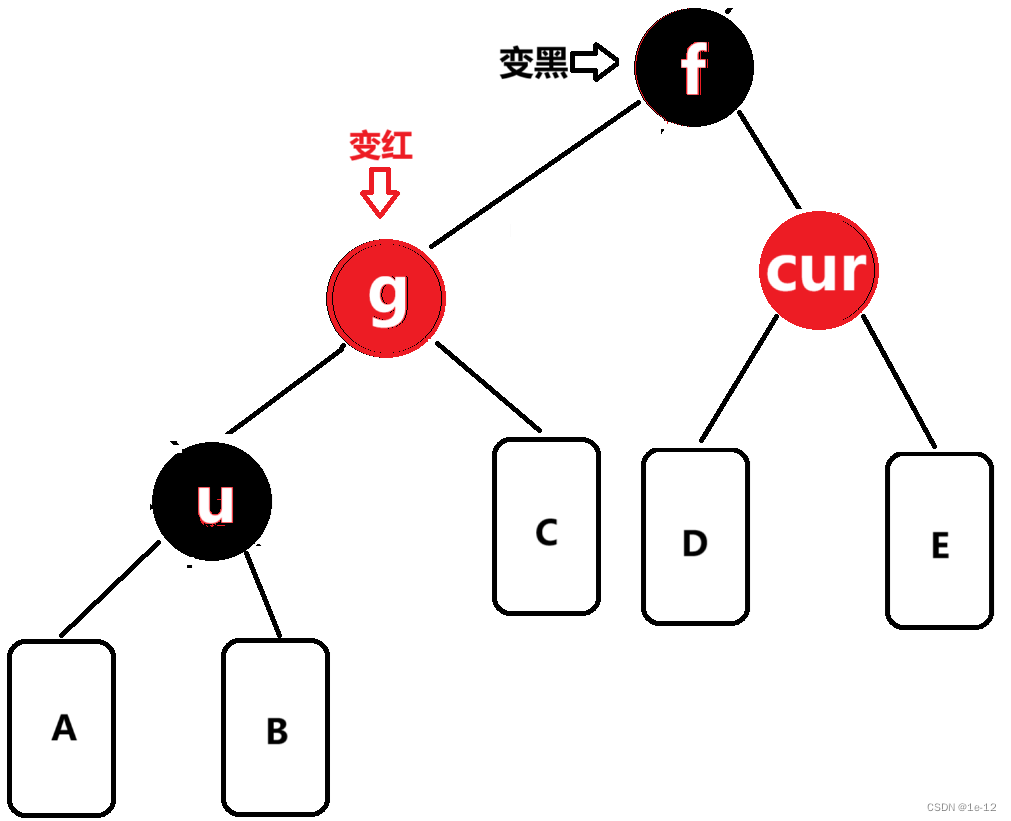
3.2.1.2.2 g、f、cur构成一条折线
f为g的左孩子,cur为f的右孩子,则做左右双旋,旋转完后将cur节点颜色置黑、g节点颜色置红:
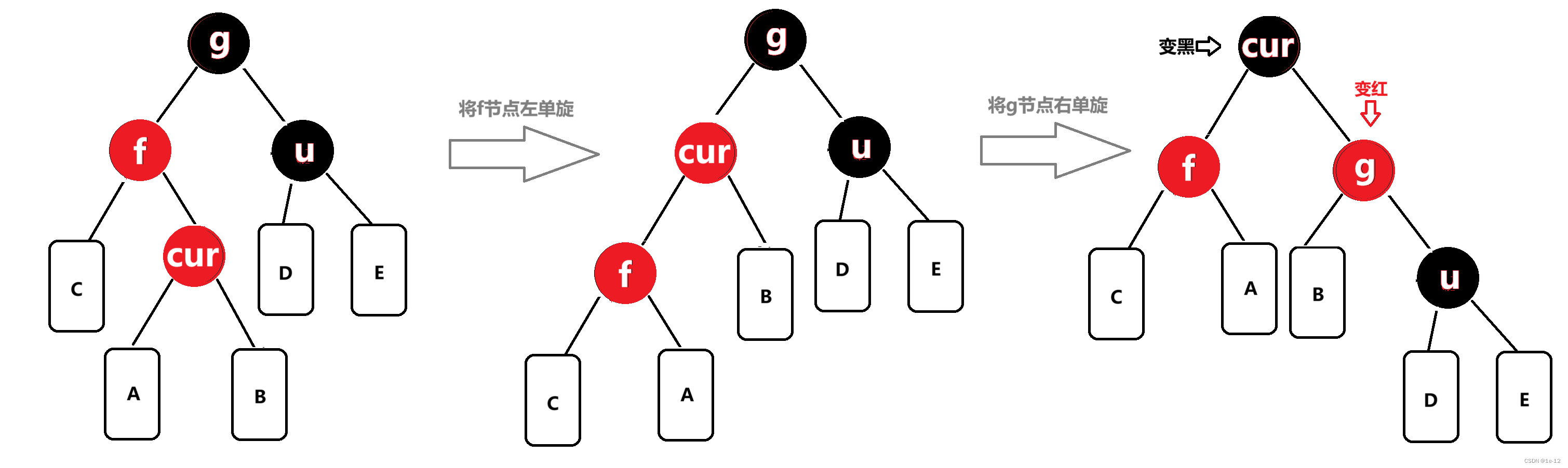
相反, f为g的右孩子,cur为f的左孩子,则做右左双旋,旋转完后将cur节点颜色置黑、g节点颜色置红:
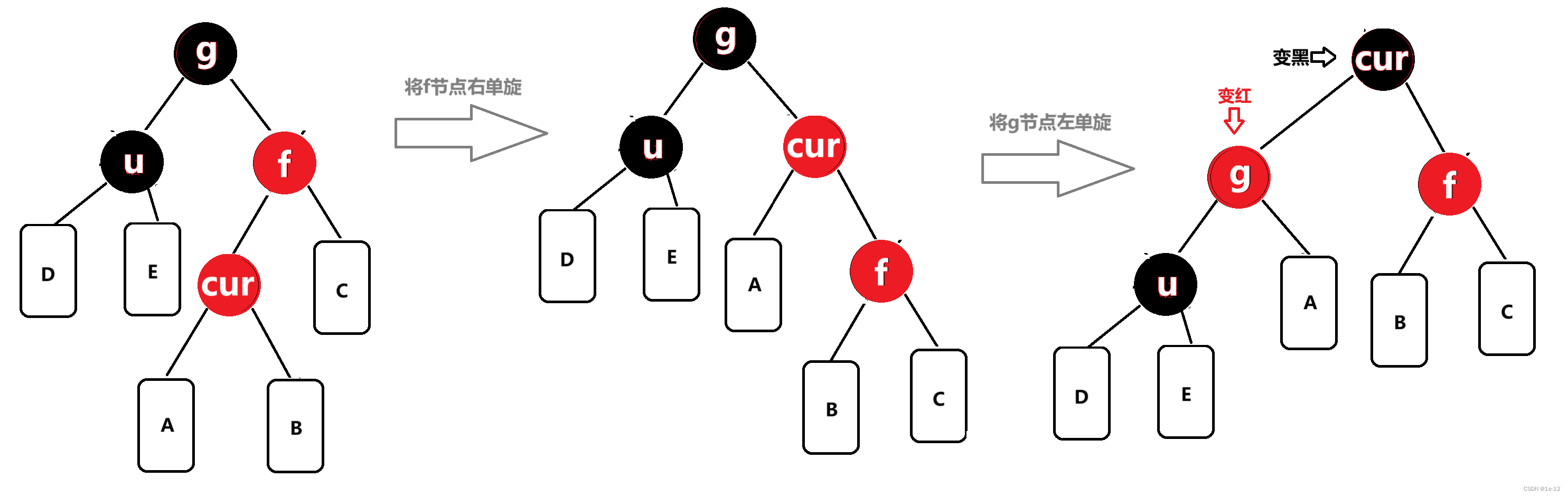
对于旋转操作还不熟悉的同学可以看到这里:【数据结构高阶】AVL树
3.2.2 调整部分的代码实现
template<class Key, class Val>
class RBTree
{typedef RBTreeNode<Key, Val> Node;
public:bool Insert(const pair<Key, Val>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* cur = _root, * parent = nullptr;while (cur)//找到合适的位置{if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else{cout << "插入的值重复" << endl;return false;}}cur = new Node(kv);//将插入的节点连接上二叉树if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;//开始调整while (parent && parent->_col == RED)//红黑树的结构出现两个连续的红色节点{Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED)//cur为红,p为红,g为黑,u存在且为红{parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;//继续向上更新cur = grandfather;parent = cur->_parent;}elsecur为红,p为红,g为黑,u不存在/u存在且为黑{if (cur == parent->_left)//cur在p的左边,p也在g的左边,构成一条直线{//右单旋RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else//cur在p的右边,p在g的左边,构成一条折线{//左右双旋RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;//调整完跳出}}else{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED)//cur为红,p为红,g为黑,u存在且为红{parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;//继续向上更新cur = grandfather;parent = cur->_parent;}elsecur为红,p为红,g为黑,u不存在/u存在且为黑{if (cur == parent->_right)//cur在p的右边,p也在g的右边,构成一条直线{//左单旋RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else//cur在p的左边,p在g的右边,构成一条折线{//右左双旋RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;//调整完跳出}}}_root->_col = BLACK;//确保即便进行过调整后根节点颜色为黑return true;
}private:void RotateL(Node* parent)//左单旋{Node* subR = parent->_right;Node* subRL = subR->_left;Node* pparent = parent->_parent;parent->_right = subRL;//更新parent的右节点if (subRL)//防止该节点为空{subRL->_parent = parent;//更新subRL的父节点}parent->_parent = subR;//更新parent的父节点subR->_left = parent;//subR的左子树置为parentsubR->_parent = pparent;//更新subR的父节点if (pparent == nullptr)//旋转的是整棵树{_root = subR;//更新根节点}else//将旋转后的子树链接上整个二叉树{if (pparent->_left == parent){pparent->_left = subR;}else{pparent->_right = subR;}}}void RotateR(Node* parent)//右单旋{Node* subL = parent->_left;Node* subLR = subL->_right;Node* pparent = parent->_parent;parent->_left = subLR;//更新parent的左节点if (subLR)//防止该节点为空{subLR->_parent = parent;//更新subLR的父节点}parent->_parent = subL;//更新parent的父节点subL->_right = parent;//subL的右子树置为parentsubL->_parent = pparent;//更新subL的父节点if (pparent == nullptr)//旋转的是整棵树{_root = subL;//更新根节点}else//将旋转后的子树链接上整个二叉树{if (pparent->_left == parent){pparent->_left = subL;}else{pparent->_right = subL;}}}private:Node* _root = nullptr;
};
3.3 红黑树的验证
下面我们来写段代码来验证一课树是不是红黑树:
template<class Key, class Val>
class RBTree
{typedef RBTreeNode<Key, Val> Node;
public:bool IsBalance(){if (_root && _root->_col == RED){cout << "根节点颜色是红色" << endl;return false;}int benchmark = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK)++benchmark;cur = cur->_left;}// 连续红色节点return _Check(_root, 0, benchmark);}private:bool _Check(Node* root, int blackNum, int benchmark)//计算每条路径上黑色节点的个数{if (root == nullptr){if (benchmark != blackNum){cout << "某条路径黑色节点的数量不相等" << endl;return false;}return true;}if (root->_col == BLACK){++blackNum;}if (root->_col == RED&& root->_parent&& root->_parent->_col == RED){cout << "存在连续的红色节点" << endl;return false;}return _Check(root->_left, blackNum, benchmark)&& _Check(root->_right, blackNum, benchmark);}private:Node* _root = nullptr;
};
3.4 测试代码
void Test_RBTree()
{const size_t N = 50000;RBTree<int, int> t;for (size_t i = 0; i < N; ++i){size_t x = rand() + i;t.Insert(make_pair(x, x));}t.InOrder();cout << t.IsBalance();
}int main()
{Test_RBTree();return 0;
}测试效果:

四、红黑树实现完整代码
#include<iostream>using namespace std;enum Colour
{RED,BLACK
};template<class Key, class Val>
struct RBTreeNode
{RBTreeNode<Key, Val>* _left;RBTreeNode<Key, Val>* _right;RBTreeNode<Key, Val>* _parent;//多一个指针指向其父节点,方便我们的后续操作pair<Key, Val> _kv;Colour _col;//颜色标识RBTreeNode(const pair<Key, Val>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_col(RED)//默认构造时,优先将节点的颜色置为红色{}
};template<class Key, class Val>
class RBTree
{typedef RBTreeNode<Key, Val> Node;
public:bool Insert(const pair<Key, Val>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* cur = _root, * parent = nullptr;while (cur)//找到合适的位置{if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else{cout << "插入的值重复" << endl;return false;}}cur = new Node(kv);//将插入的节点连接上二叉树if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;//开始调整while (parent && parent->_col == RED)//红黑树的结构出现两个连续的红色节点{Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED)//cur为红,p为红,g为黑,u存在且为红{parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;//继续向上更新cur = grandfather;parent = cur->_parent;}elsecur为红,p为红,g为黑,u不存在/u存在且为黑{if (cur == parent->_left)//cur在p的左边,p也在g的左边,构成一条直线{//右单旋RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else//cur在p的右边,p在g的左边,构成一条折线{//左右双旋RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;//调整完跳出}}else{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED)//cur为红,p为红,g为黑,u存在且为红{parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;//继续向上更新cur = grandfather;parent = cur->_parent;}elsecur为红,p为红,g为黑,u不存在/u存在且为黑{if (cur == parent->_right)//cur在p的右边,p也在g的右边,构成一条直线{//左单旋RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else//cur在p的左边,p在g的右边,构成一条折线{//右左双旋RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;//调整完跳出}}}_root->_col = BLACK;//确保即便进行过调整后根节点颜色为黑return true;
}void InOrder()//中序遍历{_InOrder(_root);cout << endl;}bool IsBalance(){if (_root && _root->_col == RED){cout << "根节点颜色是红色" << endl;return false;}int benchmark = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK)++benchmark;cur = cur->_left;}// 连续红色节点return _Check(_root, 0, benchmark);}private:void RotateL(Node* parent)//左单旋{Node* subR = parent->_right;Node* subRL = subR->_left;Node* pparent = parent->_parent;parent->_right = subRL;//更新parent的右节点if (subRL)//防止该节点为空{subRL->_parent = parent;//更新subRL的父节点}parent->_parent = subR;//更新parent的父节点subR->_left = parent;//subR的左子树置为parentsubR->_parent = pparent;//更新subR的父节点if (pparent == nullptr)//旋转的是整棵树{_root = subR;//更新根节点}else//将旋转后的子树链接上整个二叉树{if (pparent->_left == parent){pparent->_left = subR;}else{pparent->_right = subR;}}}void RotateR(Node* parent)//右单旋{Node* subL = parent->_left;Node* subLR = subL->_right;Node* pparent = parent->_parent;parent->_left = subLR;//更新parent的左节点if (subLR)//防止该节点为空{subLR->_parent = parent;//更新subLR的父节点}parent->_parent = subL;//更新parent的父节点subL->_right = parent;//subL的右子树置为parentsubL->_parent = pparent;//更新subL的父节点if (pparent == nullptr)//旋转的是整棵树{_root = subL;//更新根节点}else//将旋转后的子树链接上整个二叉树{if (pparent->_left == parent){pparent->_left = subL;}else{pparent->_right = subL;}}}void _InOrder(Node* root){if (root == NULL)//如果是空树就直接结束{return;}_InOrder(root->_left);//先递归遍历其左子树cout << root->_kv.first << " ";//再遍历其根节点_InOrder(root->_right);//最后递归遍历其右子树}bool _Check(Node* root, int blackNum, int benchmark){if (root == nullptr){if (benchmark != blackNum){cout << "某条路径黑色节点的数量不相等" << endl;return false;}return true;}if (root->_col == BLACK){++blackNum;}if (root->_col == RED&& root->_parent&& root->_parent->_col == RED){cout << "存在连续的红色节点" << endl;return false;}return _Check(root->_left, blackNum, benchmark)&& _Check(root->_right, blackNum, benchmark);}private:Node* _root = nullptr;
};相关文章:

【数据结构高阶】红黑树
目录 一、红黑树的概念 二、红黑树的性质 2.1 红黑树与AVL树的比较 三、红黑树的实现 3.1 红黑树节点的定义 3.2 数据的插入 3.2.1 红黑树的调整思路 3.2.1.1 cur为红,f为红,g为黑,u存在且为红 3.2.1.2 cur为红,f为红&am…...
Unity中Batching优化的GPU实例化(1)
文章目录 前言一、GPU实例化的规则1、网格一样,材质一样,但是材质属性不一样2、单个合批最大上限为511个对象3、只有OpenGL es 3.0及以上才支持(3.0及以上有部分硬件可能也不支持) 二、GPU实例化的应用场景1、公开几个成员属性&am…...

vue的data
类型:Object | Function 限制:组件的定义只接受 function。 详细: Vue 实例的数据对象。Vue 会递归地把 data 的 property 转换为 getter/setter,从而让 data 的 property 能够响应数据变化。对象必须是纯粹的对象 (含有零个或多个…...
Java基础课的中下基础课04
目录 二十三、集合相关 23.1 集合 (1)集合的分支 23.2 List有序可重复集合 (1)ArrayList类 (2)泛型 (3)ArrayList常用方法 (4)Vector类 (…...
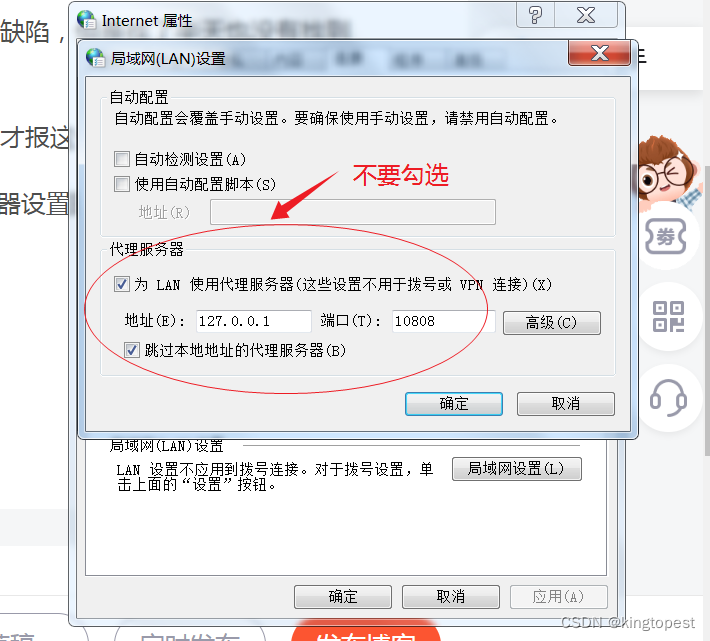
解决vue ssr服务端渲染运行时报错:net::ERR_PROXY_CONNECTION_FAILED
现象: 从代码里找了半天也没有找到问题,但是由于ssr服务端渲染配置本身非常复杂,步骤又繁琐, 而且报错又很多,不知道哪里出了问题。 感觉是header或者cookie丢失造成的,因为据说ssr本身有这样的缺陷&…...

APIFox:打造高效便捷的API管理工具
随着互联网技术的不断发展,API(应用程序接口)已经成为了企业间数据交互的重要方式。然而,API的管理和维护却成为了开发者们面临的一大挑战。为了解决这一问题,APIFox应运而生,它是一款专为API管理而生的工具…...

半导体划片机助力氧化铝陶瓷片切割:科技与工艺的完美结合
在当今半导体制造领域,氧化铝陶瓷片作为一种高性能、高可靠性的材料,被广泛应用于各种电子设备中。而半导体划片机的出现,则为氧化铝陶瓷片的切割提供了新的解决方案,实现了科技与工艺的完美结合。 氧化铝陶瓷片是一种以氧化铝为基…...

java访问数据库的库和API概述
Java & Databases: An Overview of Libraries & APIs:https://www.marcobehler.com/guides/java-databases 这篇文章对JAVA访问数据库的库和API进行了一个概述,由低层访问数据库到通过框架访问的自然演进。每一部分都介绍了简单的概念、使用片段…...

如何实现远程公共网络下访问Windows Node.js服务端
文章目录 前言1.安装Node.js环境2.创建node.js服务3. 访问node.js 服务4.内网穿透4.1 安装配置cpolar内网穿透4.2 创建隧道映射本地端口 5.固定公网地址 前言 Node.js 是能够在服务器端运行 JavaScript 的开放源代码、跨平台运行环境。Node.js 由 OpenJS Foundation࿰…...

Java架构师系统架构设计服务拆分应用
目录 1 概论2 微服务应用的分层架构3 不同维度对服务进行拆分4 新零售业务的微服务拆分5 理解微服务的无状态化6 接口版本控制实现向后兼容7 可用性的保障手段-流量整形8 设计网关层限流和分布式限流9 EDA事件驱动简述10 EDA事件驱动构建的实时账务系统11 微服务的数据一致性-B…...

盛域宏数合伙人张天:AI时代,数字化要以AI重构
大数据产业创新服务媒体 ——聚焦数据 改变商业 在这个飞速发展的科技时代,数字化已经深刻地改变了我们的生活和商业方式。信息技术的迅猛发展使得数据成为现代社会最宝贵的资源之一。数字化已经不再是可选项,而是企业持续发展的必由之路。背靠着数据的…...

Vue自定义指令插槽作用域插槽具名插槽
Vue自定义指令&插槽&作用域插槽&具名插槽 一、学习目标 1.自定义指令 基本语法(全局、局部注册)指令的值v-loading的指令封装 2.插槽 默认插槽具名插槽作用域插槽 3.综合案例:商品列表 MyTag组件封装MyTable组件封装 4.路…...
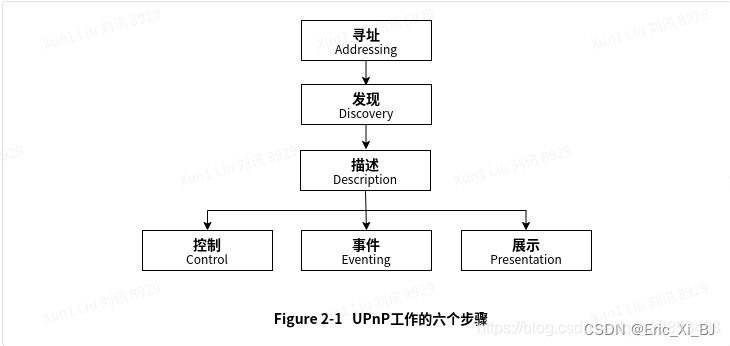
WIFI直连(Wi-Fi P2P)
一、概述 Wifi peer-to-peer(也称Wifi-Direct)是Wifi联盟推出的一项基于原来WIfi技术的可以让设备与设备间直接连接的技术,使用户不需要借助局域网或者AP(Access Point)就可以进行一对一或一对多通信。这种技术的应用…...

基于Spring+Spring boot的SpringBoot在线电子商城管理系统
SSM毕设分享 基于SpringSpring boot的SpringBoot在线电子商城管理系统 1 项目简介 Hi,各位同学好,这里是郑师兄! 今天向大家分享一个毕业设计项目作品【基于SpringSpring boot的SpringBoot在线电子商城管理系统】 师兄根据实现的难度和等级…...

【稳定检索|投稿优惠】2024年光电信息与机器人发展国际会议(ICOIRD 2024)
2024年光电信息与机器人发展国际会议(ICOIRD 2024) 2024 International Conference on Optoelectronic Information and Robot Development(ICOIRD 2024) 一、【会议简介】 信息技术与人工智能的浪潮正在激荡,不断刷新我们生活的页面,深刻烙印在光电信息…...
操作 Excel 详解)
《python每天一小段》-- (11)操作 Excel 详解
欢迎阅读《Python每天一小段》系列!在本篇文章中,将使用Python编写自动化 Excel 操作的程序。 文章目录 (1)Python 操作 Excel 详解(2)创建 DataFrame 对象(3)读取 Excel 文件&#…...

一文读懂MySQL基础知识文集(8)
🏆作者简介,普修罗双战士,一直追求不断学习和成长,在技术的道路上持续探索和实践。 🏆多年互联网行业从业经验,历任核心研发工程师,项目技术负责人。 🎉欢迎 👍点赞✍评论…...
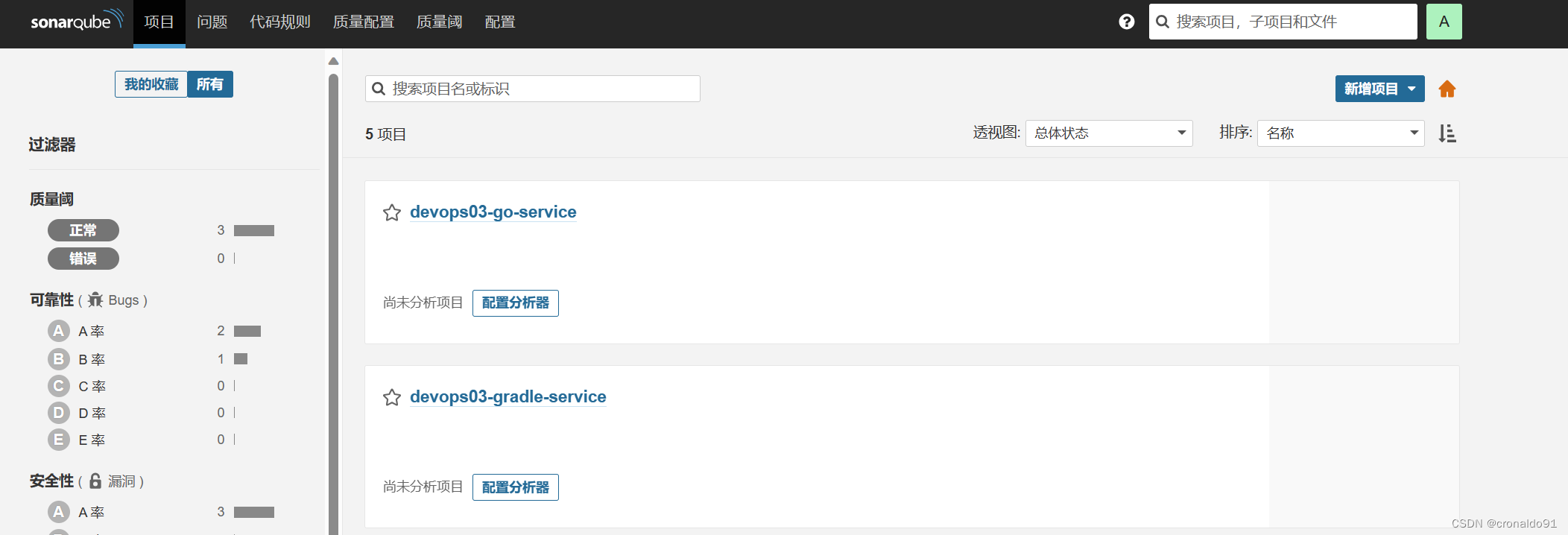
持续集成交付CICD: Sonarqube REST API 查找与新增项目
目录 一、实验 1.SonarQube REST API 查找项目 2.SonarQube REST API 新增项目 一、实验 1.SonarQube REST API 查找项目 (1)Postman测试 转换成cURL代码 (2)Jenkins添加凭证 (3)修改流水线 pipeline…...
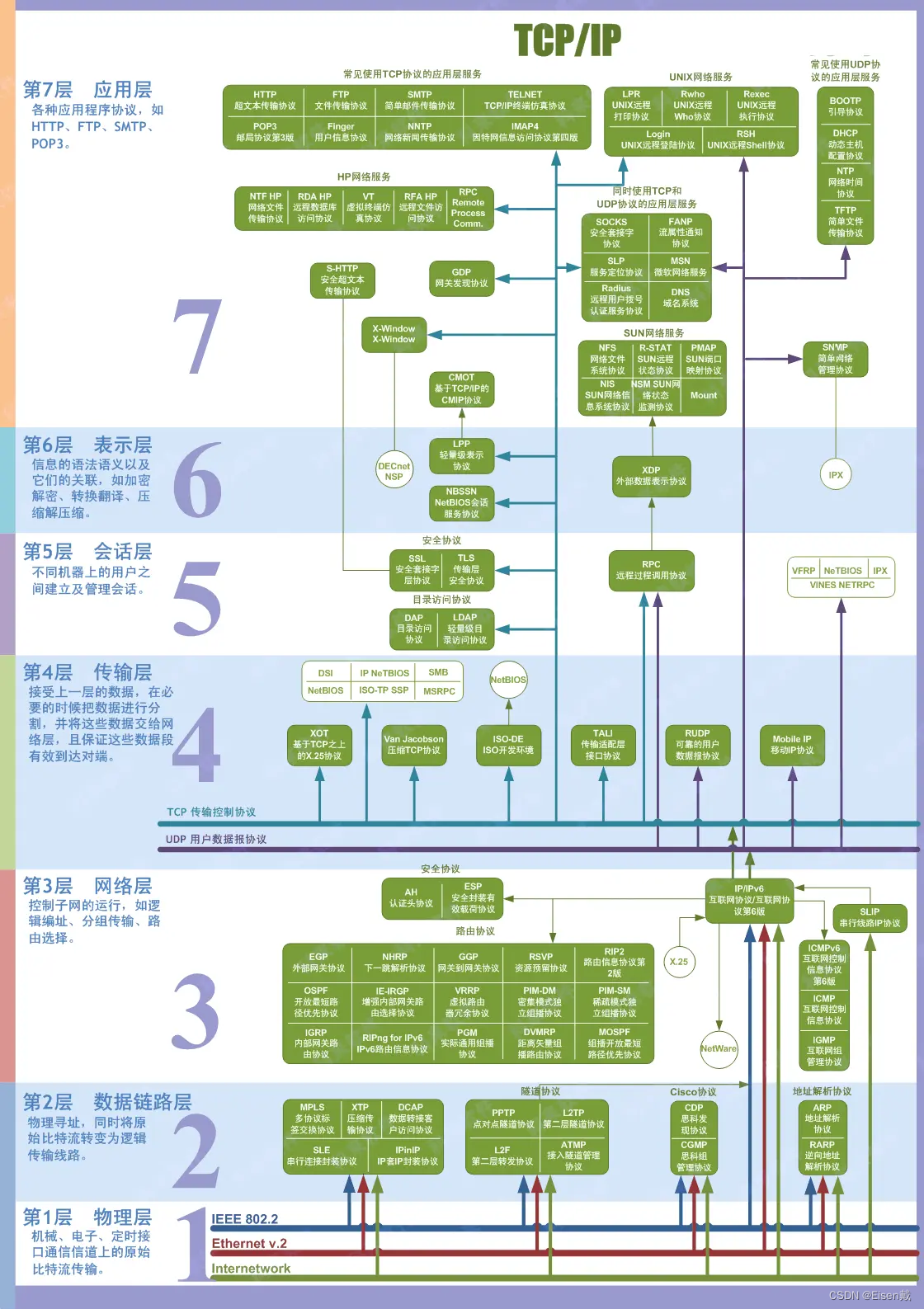
分层网络模型(OSI、TCP/IP)及对应的网络协议
OSI七层网络模型 OSI(Open System Interconnect),即开放式系统互连参考模型, 一般都叫OSI参考模型,是ISO组织于1985年研究的网络互连模型。OSI是分层的体系结构,每一层是一个模块,用于完成某种功…...

如何衡量和提高测试覆盖率?
衡量和提高测试覆盖率,对于尽早发现软件缺陷、提高软件质量和用户满意度,都具有重要意义。如果测试覆盖率低,意味着用例未覆盖到产品的所有代码路径和场景,这可能导致未及时发现潜在缺陷,代码中可能存在逻辑错误、边界…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
