DFS、BFS求解leetcode图像渲染问题(Java)
目录
leetcode733题.图像渲染
DFS
BFS
leetcode733题.图像渲染
733. 图像渲染 - 力扣(LeetCode)
有一幅以
m x n的二维整数数组表示的图画image,其中image[i][j]表示该图画的像素值大小。你也被给予三个整数
sr,sc和newColor。你应该从像素image[sr][sc]开始对图像进行 上色填充 。为了完成 上色工作 ,从初始像素开始,记录初始坐标的 上下左右四个方向上 像素值与初始坐标相同的相连像素点,接着再记录这四个方向上符合条件的像素点与他们对应 四个方向上 像素值与初始坐标相同的相连像素点,……,重复该过程。将所有有记录的像素点的颜色值改为
newColor。最后返回 经过上色渲染后的图像 。
示例 1:
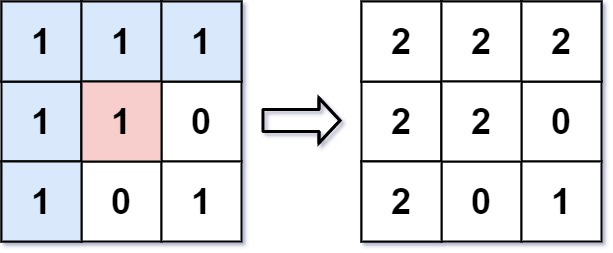
输入: image = [[1,1,1],[1,1,0],[1,0,1]],sr = 1, sc = 1, newColor = 2 输出: [[2,2,2],[2,2,0],[2,0,1]] 解析: 在图像的正中间,(坐标(sr,sc)=(1,1)),在路径上所有符合条件的像素点的颜色都被更改成2。 注意,右下角的像素没有更改为2,因为它不是在上下左右四个方向上与初始点相连的像素点。示例 2:
输入: image = [[0,0,0],[0,0,0]], sr = 0, sc = 0, newColor = 2 输出: [[2,2,2],[2,2,2]]提示:
m == image.lengthn == image[i].length1 <= m, n <= 500 <= image[i][j], newColor < 2160 <= sr < m0 <= sc < n
题目解析:一个矩阵,大小是M*N ,在[sr][sc]处涂色,(sr即row,横坐标 ;sc即column,纵坐标)但是要涂的颜色不能和他本来的颜色一样 ,如果在一个元素的前后左右跟他颜色是一样的话,那可以被涂上新颜色。
DFS
- 创建一个与图像大小相同的布尔数组,用于标记已经访问过的像素。
- 调用dfs方法进行深度优先搜索,将起始点的像素颜色替换为目标颜色,并标记为已访问。
- 在dfs方法中,递归地对起始点的上下左右四个方向进行搜索,将与起始点颜色相同且未访问过的像素替换为目标颜色,并标记为已访问。
- 最终返回填充后的图像数组。
- 在给定的解决方案中,val代表的是起始点(sr, sc)的原始颜色值。在深度优先搜索的过程中,会检查当前像素的颜色是否与val相同,如果相同则将其替换为目标颜色color。val的作用是用来判断当前像素的颜色是否与起始点的颜色相同,从而进行相应的填充操作。
-
在给定的代码中,判断条件是i >= 0和j >= 0,而不是i > 0和j > 0的原因是因为数组的索引是从0开始的。在Java中,数组的索引从0开始,因此当i和j等于0时,表示数组的第一个元素。因此,为了确保不越界,需要使用i >= 0和j >= 0作为条件,以防止访问数组的负索引。如果使用i > 0和j > 0作为条件,那么在i或j等于0时,就会跳过数组的第一行或第一列,这显然是不正确的。因此,应该使用i >= 0和j >= 0作为条件,以确保正确地访问数组中的元素。
class Solution {public int[][] floodFill(int[][] image, int sr, int sc, int color) {int m = image.length;int n = image[0].length;boolean[][] booleans = new boolean[m][n];dfs(image,booleans,sr,sc,color,image[sr][sc]);return image;}public void dfs(int[][] image,boolean[][] booleans,int i,int j,int color,int val){if (i >= 0 && j >= 0 && i < image.length && j< image[0].length&& !booleans[i][j] && image[i][j] == val) {booleans[i][j] = true;image[i][j] = color;dfs(image,booleans,i+1,j,color,val);dfs(image,booleans,i-1,j,color,val);dfs(image,booleans,i,j+1,color,val);dfs(image,booleans,i,j-1,color,val);}}
}BFS
class Solution {public int[][] floodFill(int[][] image, int sr, int sc, int color) {//以这个元素为中心 把符合要求的上下左右元素的 “坐标” 塞到队列里 同时把他现在的颜色记录下来//被涂过颜色的变成color了 没被涂过颜色的之前已经被记录下来了if(image==null || image.length==0 || image[0].length==0 || image[sr][sc]==color)//如果 二维数组是不存在的 || 二维数组的深度↓是0 || 二维数组的宽度→是0 || 要涂的元素正好是新颜色 {return image;//那就不做}int m= image.length-1;//获取整个二维数组的最深下标↓//二维数组.length -> 有多少个一维数组 也就是深度int n= image[0].length-1;//获取整个二维数组的最远下标→//二维数组[0].length -> 每个一维数组的长度是多少int oldcolor = image[sr][sc];//先把当前的颜色记住 这个是原来的颜色Queue<int []> queue = new LinkedList();//先整一个队列 这个队列里面放的是符合条件的元素的“坐标”queue.offer(new int[] {sr,sc} );//把一开始要我们涂的元素的坐标记录下来 塞到队列里去 while(!queue.isEmpty())//如果队列不空 也就是还有元素要被涂色{int point []= queue.poll();//让元素出队 获取元素的坐标//{i,j} i是这个元素的横坐标 j是纵坐标int i = point[0];//获取横坐标int j = point[1];//获取纵坐标//i是管上下的 j是管左右的image[i][j]=color;//给元素上色//这个点的上下左右找//最左边的下标就是0 最右边的下标就是n//最上边的下标就是0 最下边的下标就是mif(i-1>=0 && image[i-1][j]==oldcolor)//如果向下移动不越界 且 他左边的元素没有被涂过色{queue.offer(new int[]{i-1,j});//那么就把他下边的元素的“坐标”记录下来 入队}if(i+1<=m && image[i+1][j]==oldcolor)//如果向上移动不越界 且 他右边的元素没有被涂过色{queue.offer(new int[]{i+1,j});//那么就把他上边的元素的“坐标”记录下来 入队}if(j-1>=0 && image[i][j-1]==oldcolor)//如果向左移动不越界 且 他上边的元素没有被涂过色 {queue.offer(new int[]{i,j-1});//那么就把他左边的元素的“坐标”记录下来 入队}if(j+1<=n && image[i][j+1]==oldcolor)//如果向右移动不越界 且 他下边的元素没有被涂过色{queue.offer(new int[]{i,j+1});//那么就把他右边的元素的“坐标”记录下来 入队}}//做完了就返回该二维数组 return image;}
}//来个没那么多注释的 显得整洁
class Solution {public int[][] floodFill(int[][] image, int sr, int sc, int color) {if(image==null || image.length==0 || image[0].length==0 || image[sr][sc]==color){return image;}int m= image.length-1;int n= image[0].length-1;int oldcolor = image[sr][sc];Queue<int []> queue = new LinkedList();//这个队列里面放的是符合条件的元素的坐标queue.offer(new int[] {sr,sc} ); while(!queue.isEmpty())//如果队列不空 也就是还有元素要被涂色{int point []= queue.poll();int i = point[0];//获取横坐标int j = point[1];//获取纵坐标//i是管上下的 j是管左右的image[i][j]=color;//给元素上色//最左边的下标就是0 最右边的下标就是n//最上边的下标就是0 最下边的下标就是mif(i-1>=0 && image[i-1][j]==oldcolor){queue.offer(new int[]{i-1,j});}if(i+1<=m && image[i+1][j]==oldcolor){queue.offer(new int[]{i+1,j});}if(j-1>=0 && image[i][j-1]==oldcolor){queue.offer(new int[]{i,j-1});}if(j+1<=n && image[i][j+1]==oldcolor){queue.offer(new int[]{i,j+1});}}return image;}
}相关文章:
DFS、BFS求解leetcode图像渲染问题(Java)
目录 leetcode733题.图像渲染 DFS BFS leetcode733题.图像渲染 733. 图像渲染 - 力扣(LeetCode) 有一幅以 m x n 的二维整数数组表示的图画 image ,其中 image[i][j] 表示该图画的像素值大小。 你也被给予三个整数 sr , sc 和 newColor …...
0基础学习云计算难吗?
很多人经常会问云计算是什么?云计算能干什么?学习云计算能做什么工作?其实我们有很多人并不知道云计算是什么,小知今天来给大家讲讲学习云计算能做什么。 中国的云计算行业目前正处于快速发展阶段,随着互联网和数字化…...

【RabbitMQ高级功能详解以及常用插件实战】
文章目录 队列1 、Classic经典队列2、Quorum仲裁队列3、Stream流式队列4、如何使用不同类型的队列 二、死信队列 队列 classic经典队列,Quorum仲裁队列,Stream流式队列 1 、Classic经典队列 这是RabbitMQ最为经典的队列类型。在单机环境中,…...
开源的数据流技术,该选择Redpanda还是Apache Kafka?
本文将比较Apache Kafka和Redpanda两种开源的数据流技术,在云原生实时处理能力上的不同,以及如何在项目中做出选择。 目前,Apache Kafka不但成为了数据流处理领域事实上的标准,而且带动了同类产品的出现。Redpanda就是其中之一…...

720度vr虚拟家居展厅提升客户的参观兴致
VR虚拟展厅线上3D交互展示的优势有以下几点: 打破了场馆的展示限制,可展示危险性制品、珍贵稀有物品、超大型设备等,同时提供了更大的展示空间和更丰富的展示内容。 可提供企业真实环境的实时VR全景参观,提升潜在客户信任度。 提供…...
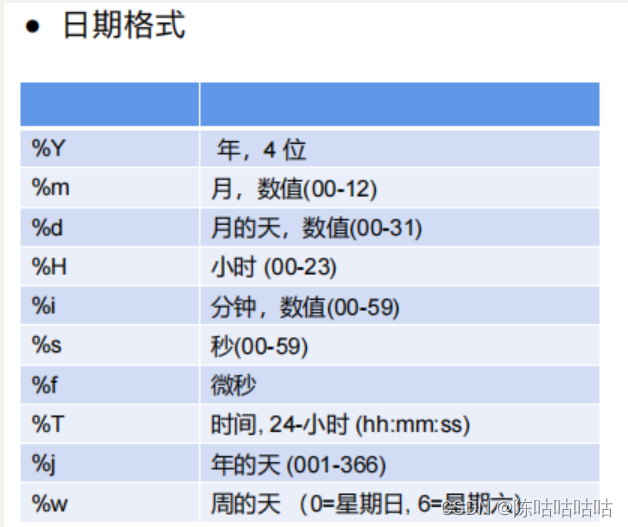
mysql中的DQL查询
表格为: DQL 基础查询 语法:select 查询列表 from 表名:(查询的结果是一个虚拟表格) -- 查询指定的列 SELECT NAME,birthday,phone FROM student -- 查询所有的列 * 所有的列, 查询结果是虚拟的表格&am…...

【数据结构高阶】红黑树
目录 一、红黑树的概念 二、红黑树的性质 2.1 红黑树与AVL树的比较 三、红黑树的实现 3.1 红黑树节点的定义 3.2 数据的插入 3.2.1 红黑树的调整思路 3.2.1.1 cur为红,f为红,g为黑,u存在且为红 3.2.1.2 cur为红,f为红&am…...
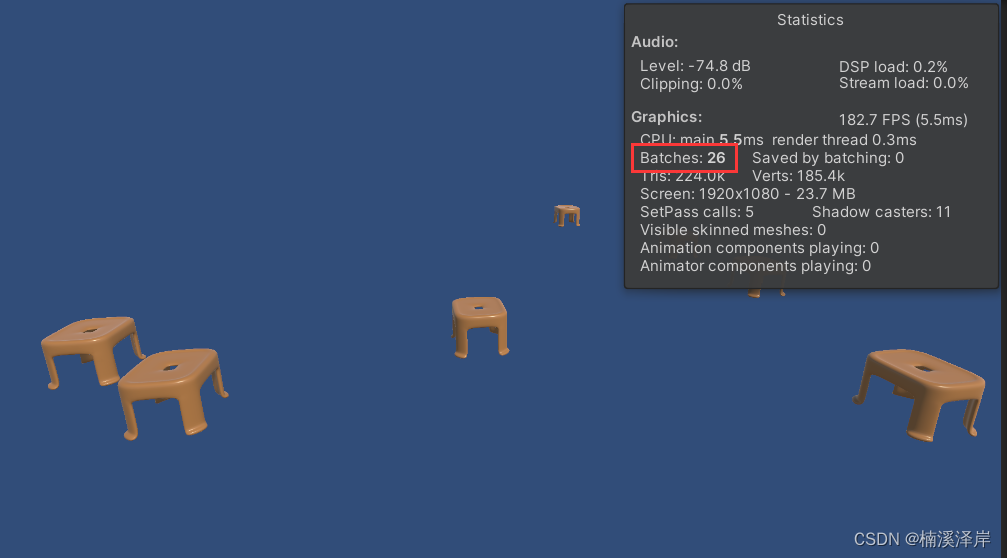
Unity中Batching优化的GPU实例化(1)
文章目录 前言一、GPU实例化的规则1、网格一样,材质一样,但是材质属性不一样2、单个合批最大上限为511个对象3、只有OpenGL es 3.0及以上才支持(3.0及以上有部分硬件可能也不支持) 二、GPU实例化的应用场景1、公开几个成员属性&am…...

vue的data
类型:Object | Function 限制:组件的定义只接受 function。 详细: Vue 实例的数据对象。Vue 会递归地把 data 的 property 转换为 getter/setter,从而让 data 的 property 能够响应数据变化。对象必须是纯粹的对象 (含有零个或多个…...
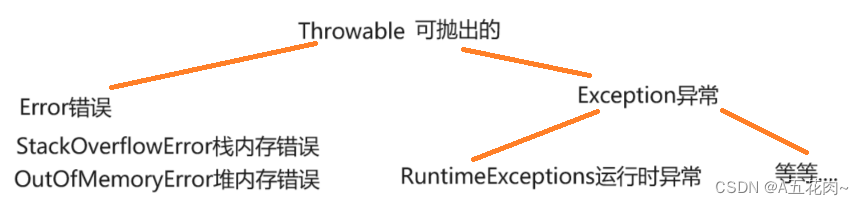
Java基础课的中下基础课04
目录 二十三、集合相关 23.1 集合 (1)集合的分支 23.2 List有序可重复集合 (1)ArrayList类 (2)泛型 (3)ArrayList常用方法 (4)Vector类 (…...
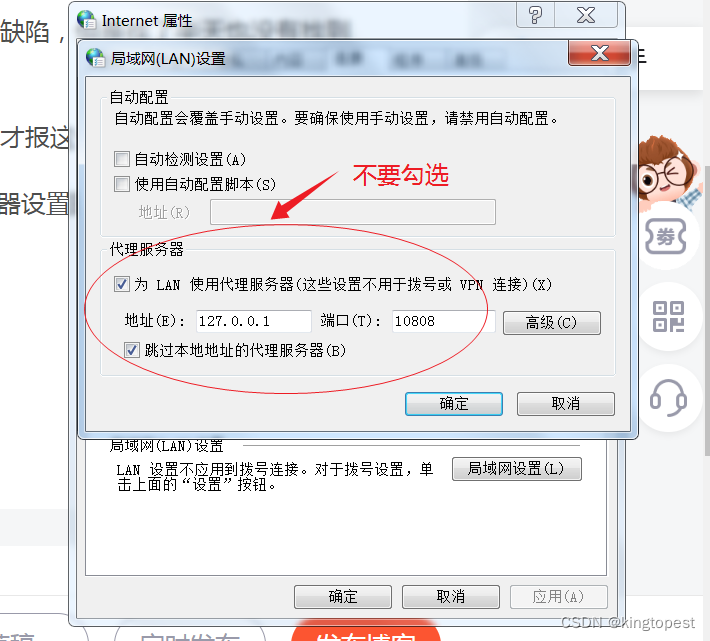
解决vue ssr服务端渲染运行时报错:net::ERR_PROXY_CONNECTION_FAILED
现象: 从代码里找了半天也没有找到问题,但是由于ssr服务端渲染配置本身非常复杂,步骤又繁琐, 而且报错又很多,不知道哪里出了问题。 感觉是header或者cookie丢失造成的,因为据说ssr本身有这样的缺陷&…...

APIFox:打造高效便捷的API管理工具
随着互联网技术的不断发展,API(应用程序接口)已经成为了企业间数据交互的重要方式。然而,API的管理和维护却成为了开发者们面临的一大挑战。为了解决这一问题,APIFox应运而生,它是一款专为API管理而生的工具…...

半导体划片机助力氧化铝陶瓷片切割:科技与工艺的完美结合
在当今半导体制造领域,氧化铝陶瓷片作为一种高性能、高可靠性的材料,被广泛应用于各种电子设备中。而半导体划片机的出现,则为氧化铝陶瓷片的切割提供了新的解决方案,实现了科技与工艺的完美结合。 氧化铝陶瓷片是一种以氧化铝为基…...

java访问数据库的库和API概述
Java & Databases: An Overview of Libraries & APIs:https://www.marcobehler.com/guides/java-databases 这篇文章对JAVA访问数据库的库和API进行了一个概述,由低层访问数据库到通过框架访问的自然演进。每一部分都介绍了简单的概念、使用片段…...

如何实现远程公共网络下访问Windows Node.js服务端
文章目录 前言1.安装Node.js环境2.创建node.js服务3. 访问node.js 服务4.内网穿透4.1 安装配置cpolar内网穿透4.2 创建隧道映射本地端口 5.固定公网地址 前言 Node.js 是能够在服务器端运行 JavaScript 的开放源代码、跨平台运行环境。Node.js 由 OpenJS Foundation࿰…...

Java架构师系统架构设计服务拆分应用
目录 1 概论2 微服务应用的分层架构3 不同维度对服务进行拆分4 新零售业务的微服务拆分5 理解微服务的无状态化6 接口版本控制实现向后兼容7 可用性的保障手段-流量整形8 设计网关层限流和分布式限流9 EDA事件驱动简述10 EDA事件驱动构建的实时账务系统11 微服务的数据一致性-B…...

盛域宏数合伙人张天:AI时代,数字化要以AI重构
大数据产业创新服务媒体 ——聚焦数据 改变商业 在这个飞速发展的科技时代,数字化已经深刻地改变了我们的生活和商业方式。信息技术的迅猛发展使得数据成为现代社会最宝贵的资源之一。数字化已经不再是可选项,而是企业持续发展的必由之路。背靠着数据的…...

Vue自定义指令插槽作用域插槽具名插槽
Vue自定义指令&插槽&作用域插槽&具名插槽 一、学习目标 1.自定义指令 基本语法(全局、局部注册)指令的值v-loading的指令封装 2.插槽 默认插槽具名插槽作用域插槽 3.综合案例:商品列表 MyTag组件封装MyTable组件封装 4.路…...
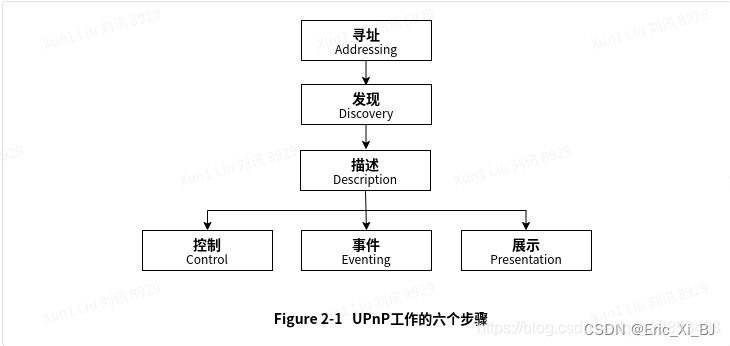
WIFI直连(Wi-Fi P2P)
一、概述 Wifi peer-to-peer(也称Wifi-Direct)是Wifi联盟推出的一项基于原来WIfi技术的可以让设备与设备间直接连接的技术,使用户不需要借助局域网或者AP(Access Point)就可以进行一对一或一对多通信。这种技术的应用…...

基于Spring+Spring boot的SpringBoot在线电子商城管理系统
SSM毕设分享 基于SpringSpring boot的SpringBoot在线电子商城管理系统 1 项目简介 Hi,各位同学好,这里是郑师兄! 今天向大家分享一个毕业设计项目作品【基于SpringSpring boot的SpringBoot在线电子商城管理系统】 师兄根据实现的难度和等级…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...
