数据结构:堆的实现与建堆时间复杂度分析
目录
前言
一.堆的介绍
1.堆的本质
2.堆的分类
二.堆的实现(以小根堆为例)
1.关于二叉树的两组重要结论:
2.堆的物理存储结构框架(动态数组的简单构建)
3. 堆元素插入接口(以小根堆为例)
堆尾元素向上调整的算法接口:
4.堆元素插入接口测试
5.堆元素插入接口建堆的时间复杂度分析(建堆时间复杂度)
6.堆元素删除接口(同样以小根堆为例子)
堆元素向下调整算法接口实现:
7.堆元素删除接口测试
8.逐个删除堆顶数据过程的时间复杂度分析(删堆的时间复杂度分析)
9.堆的实现代码总览(以小根堆为例)
10.结语
前言
关于数据结构的文章:写博客的时候我感觉在表达层面上有点费劲,如果文章整体在表述上让人感觉不够清楚,恳请读者原谅,本菜狗已经尽力了.
一.堆的介绍
1.堆的本质
关于二叉树的图论基础参见:http://t.csdn.cn/Nv325
http://t.csdn.cn/Nv325青菜友情提示:基础概念对于理解堆的实现与运用非常重要
堆的本质是映射在内存中顺序存储结构(数组)上的完全二叉树(完全二叉树是堆的逻辑结构).
堆的图解:
- 结点中的数据存储在相应下标的数组元素空间中
2.堆的分类
堆的两个类型:
- 大根堆:在大根堆中任何子结构的父结点中存储的值大于其左右孩子结点中存储的值
- 小根堆:在小根堆中任何子结构的父结点中存储的值小于其左右孩子结点中存储的值
二.堆的实现(以小根堆为例)
1.关于二叉树的两组重要结论:
- 堆的任何一个父结点的编号parent与其左孩子结点的编号leftchild满足如下关系式:
- 堆的任何一个父结点的编号parent与其右孩子结点的编号rightchild满足如下关系式:
这两组重要结论的推导和分析参见青菜的博客:http://t.csdn.cn/Nv325
http://t.csdn.cn/Nv325
2.堆的物理存储结构框架(动态数组的简单构建)
堆是存储在数组上的(大小根)完全二叉树,因此在实现堆之前我们先构建一个简单的动态数组作为物理存储结构框架:
- 维护动态数组的结构体:
typedef int HPDataType; //堆元素类型 typedef struct Heap {HPDataType* arry; //堆区内存指针size_t size; //堆元素个数size_t capacity; //数组的空间容量 }HP;- 堆的基础操作接口声明:
//维护堆的结构体的初始化接口 void HeapInit(HP* php);//销毁堆的接口 void HeapDestroy(HP* php);//堆元素的打印接口 void HeapPrint(HP* php);//判断堆是否为空(堆中有无元素)的接口 bool HeapEmpty(HP* php);//返回堆中元素个数的接口 size_t HeapSize(HP* php);//返回堆顶元素(即编号为0的元素)的接口 HPDataType HeapTop(HP* php);- 基础接口的实现:
//堆结构体的初始化接口 void HeapInit(HP* ptrheap) {assert(ptrheap);ptrheap->arry = NULL;ptrheap->capacity = 0;ptrheap->size = 0;}//销毁堆的接口 void HeapDestroy(HP* ptrheap) {assert(ptrheap);free(ptrheap->arry);ptrheap->arry = NULL;ptrheap->capacity = 0;ptrheap->size = 0; }//堆的打印接口 void HeapPrint(HP* ptrheap) {assert(ptrheap);size_t tem = 0;for (tem = 0; tem < ptrheap->size; ++tem){printf("%d->", ptrheap->arry[tem]);}printf("END\n"); }//判断堆是否为空的接口 bool HeapEmpty(HP* ptrheap) {assert(ptrheap);return (0 == ptrheap->size); }//返回堆元素个数的接口 size_t HeapSize(HP* ptrheap) {assert(ptrheap);return ptrheap->size; }//返回堆顶元素的接口 HPDataType HeapTop(HP* ptrheap) {assert(!HeapEmpty(ptrheap));return ptrheap->arry[0]; }主函数建堆时的内存布局简单图示:
堆区上的数组是在堆元素插入接口中调用malloc申请出来的(我们暂时还没有实现堆元素插入的接口)
以上是堆在内存中的存储框架的构建,然而堆的核心接口是堆元素的插入和删除接口
3. 堆元素插入接口(以小根堆为例)
- 堆的构建过程概述:向堆尾逐个插入元素(将元素尾插进数组中),每次插入一个元素后都通过堆的调整算法逐层向上(二叉树意义上的层)(子结点和父结点进行大小比较,若不满足小根堆的性质就进行数值交换)调整该元素在堆中的位置以保持小根堆的数据结构.
- 算法过程简图:
- 从0个结点的堆开始,每尾插一个元素我们都按照小根堆的性质(通过元素向上调整算法)调整该元素在堆中的位置来保持小根堆的数据结构,我们就是以这样的基本思想来建堆的.
- 建堆的思路细解:
- 显然在堆尾插入元素6后破坏了小根堆的结构(6小于其父结点20不满足小根堆的性质)(将任意一个子结构中子结点与父结点进行大小比较就可以知道堆的结构有没有被破坏),因此我们就需要将6这个元素逐层向二叉树的上层调整(每个调整的子步骤都是从子结点向父结点调整)
- 通过树的子结构中子结点与父结点的编号关系可以找到堆尾8号结点(元素6)的父结点(元素20,结点编号为3)
- 接下来将元素逐层向上调整(子结点和父结点进行数值交换)来恢复小根堆的数据结构:
向上调整的第一步:将尾插进堆尾的结点(8号结点,值为6)与其父结点(3号结点,值为20)进行比较,父结点大于子结点,交换父结点与子结点的值(下图中的Swap是元素数值交换接口):
向上调整的第二步:交换了8号结点和3号结点的值后,我们发现小堆结构依然不成立,于是重复上述的调整过程,将元素6继续向上层的父结点位置进行调整,不断重复迭代直到小堆结构恢复或者元素6被调到堆顶为止:
- 可见经过再一次调整后,元素6来到了1号结点,此时1号结点大于0号结点,小堆数据结构得到恢复,调整过程终止。
同时不难分析出,任何堆尾元素向上调整的过程都是在堆尾到堆顶元素的连通路径上进行的(该路径长度数量级为logk)(k为当前树结点总个数)):
- 根据上面的分析我们可以设计出一个堆尾元素向上调整的算法接口:
接口首部: arry是指向数组首地址的指针,child是堆尾元素的编号(结点编号同时也是该元素的数组下标)
void AdjustUp(HPDataType* arry, size_t child);堆尾元素向上调整的算法接口:
//元素交换接口 void Swap(HPDataType* e1, HPDataType* e2) {assert(e1 && e2);HPDataType tem = *e1;*e1 = *e2;*e2 = tem; }//小堆元素的向上调整接口 void AdjustUp(HPDataType* arry, size_t child) //child表示孩子结点的编号 {assert(arry);size_t parent = (child - 1) / 2; //算出父结点的数组下标(堆编号)while (child > 0) //child减小到0时则调整结束(堆尾元素已调到堆顶){if (arry[child] < arry[parent]) //父结点大于子结点,则子结点需要上调以保持小堆的结构{Swap(arry + child, arry+parent);child = parent; //将原父结点作为新的子结点继续迭代过程parent = (child - 1) / 2; //算出父结点的数组下标(堆编号)}else{break; //父结点不大于子结点,则堆结构恢复,无需再调整}} }堆尾元素向上调整的算法接口中需要注意的细节:
- 调整循环的终止条件有两个:
- 一个是被调整元素被调到了堆顶(即child=0的时候)
- 当被调整元素大于其父结点时小堆的数据结构得到恢复,break终止循环
有了该接口,我们就可以设计堆元素插入接口:
- HP * ptrheap是指向堆结构体的结构体指针,x是要插入的元素的数值
void HeapPush(HP* ptrheap, HPDataType x)// 插入一个小堆元素的接口 // 插入x以后,保持其数据结构依旧是小堆 void HeapPush(HP* ptrheap, HPDataType x) //ptrheap是指向堆结构体的结构体指针 {assert(ptrheap);if (ptrheap->capacity == ptrheap->size) //数组容量检查,容量不够则扩容{size_t newcapacity = (0 == ptrheap->capacity) ? 4 : 2 * ptrheap->capacity;//注意容量为0则将堆区数组容量调整为4HPDataType* tem = (HPDataType*)realloc(ptrheap->arry, newcapacity*sizeof(HPDataType)); //空间不够则扩容assert(tem); //检查扩容是否成功ptrheap->arry = tem; //将堆区地址赋给结构体中的指针成员ptrheap->capacity = newcapacity; //容量标记更新}ptrheap->arry[ptrheap->size] = x; //元素尾插入堆ptrheap->size++;//将尾插的元素进行向上调整以保持堆的数据结构(复用元素向上调整接口)AdjustUp(ptrheap->arry, ptrheap->size - 1); //根据完全二叉树的结构特点可知堆尾元素 //在二叉树中编号为size-1 }
- 该接口可以完成一个堆元素的插入(而且每次完成插入后小根堆的数据结构都可以得到保持)
- 如果我们想要创建一个n个元素小根堆,则n次调用HeapPush接口即可
4.堆元素插入接口测试
现在我们试着用HeapPush接口来构建六个元素的小堆,并将堆打印出来观察其逻辑结构:
- 主函数代码:
int main () {HP hp; //创建一个堆结构体HeapInit(&hp); //结构体初始化HeapPush(&hp, 1); //调用堆元素插入接口建堆HeapPush(&hp, 5);HeapPush(&hp, 0);HeapPush(&hp, 8);HeapPush(&hp, 3);HeapPush(&hp, 9);HeapPrint(&hp); //打印堆元素 }
我们来观察一下打印出来的小根堆的逻辑结构:
5.堆元素插入接口建堆的时间复杂度分析(建堆时间复杂度)
- 假设现在我们要调用HeapPush接口来创建一个N个元素的小堆(调用N次HeapPush接口)
- 注意:我们只关注时间复杂度最坏的情况(即假设每个插入堆尾的元素都沿着连通路径向上调整到了堆顶)
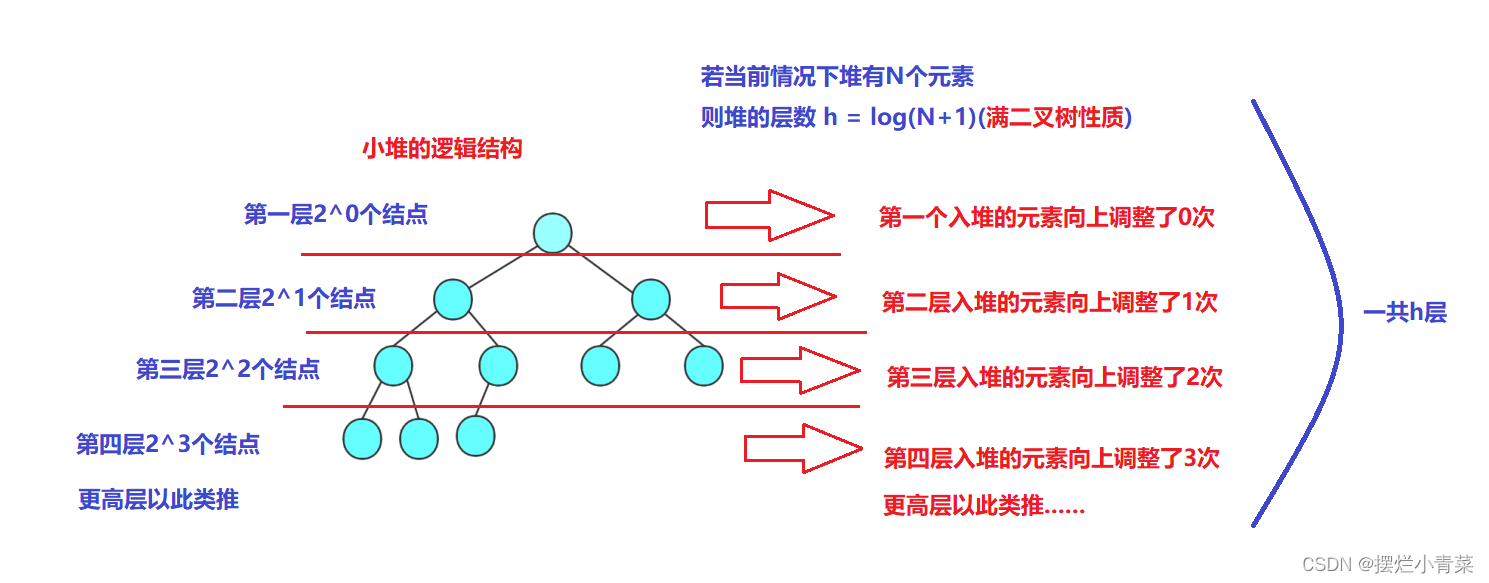
- 分析建堆的时间复杂度时我们将堆看成满二叉树(满二叉树是特殊的完全二叉树),也就是说当堆有N个元素时,堆的层数h=log(N+1)(该对数以2为底,计算机科学中我们一般不关注对数的底数)
- 接下来我们将所有元素的向上调整次数进行求和,即可得出用HeapPush接口建堆的时间复杂度:
- 用错位相减法可对上面公式进行求和计算:
- 因此可以得到用堆元素插入接口(堆元素向上调整算法)建堆(建立N个元素的小根堆)的时间复杂度为:O(N)=NlogN;
6.堆元素删除接口(同样以小根堆为例子)
我们讨论的堆元素删除指的是:删除堆顶数据
删除堆顶的元素的基本思路:
- 先将堆顶元素与堆尾元素进行交换,然后令维护堆的结构体中的size(记录堆元素个数的成员变量)减一(相当于移除堆尾元素)
- 然而原来的堆尾元素被交换到堆顶位置后,小根堆的数据结构会被破坏,因此我们需要将堆顶元素进行向下调整操作:
- 堆顶元素向下调整图解演示:
- 通过算法图解分析我们可以设计一个堆元素向下调整算法接口:
arry是指向内存堆区数组首地址的指针,size是堆的结点总个数,parent是待调整结点在堆中的编号;
void AdjustDown(HPDataType* arry,size_t size,size_t parent)堆元素向下调整算法接口实现:
//元素交换接口 void Swap(HPDataType* e1, HPDataType* e2) {assert(e1 && e2);HPDataType tem = *e1;*e1 = *e2;*e2 = tem; }//小堆元素的向下调整接口 void AdjustDown(HPDataType* arry,size_t size,size_t parent) {assert(arry);size_t child = 2 * parent + 1; //确定父结点的左孩子的编号while (child < size) //child增加到大于或等于size时说明被调整元素被调整到了叶结点上,调整过程结束{if (child + 1 < size && arry[child + 1] < arry[child])//确定左右孩子中较小的孩子结点{++child; //条件成立说明右孩子较小,child更新为右孩子编号}if ( arry[child] < arry[parent])//父结点大于子结点,则父结点需要下调以保持小堆的结构{Swap(arry + parent, arry + child);//父子结点进行值交换parent = child; //将原来的子结点作为新的父结点继续迭代过程child = 2 * parent + 1; //继续向下找另外一个子结点}else{break; //父结点不大于子结点,则小堆结构成立,无需继续调整}} }
- 注意一下算法接口的一些细节和边界条件:
- child<size说明被调整元素已经被调整到叶结点位置,结束调整过程
- 算法接口中我们只设计了一个child变量来记录当前父结点的孩子结点的编号,接着通过arry[child + 1] < arry[child]来比较左右孩子大小来确定child到底是取左孩子的编号还是取右孩子的编号(注意child+1<size判断语句是为了确定右孩子是否存在)
- 有了堆元素向下调整算法接口我们就可以实现堆顶数据删除接口:
//删除堆顶元素 void HeapPop(HP* ptrheap) {assert(ptrheap);Swap(ptrheap->arry, ptrheap->arry + ptrheap->size - 1); //交换堆顶与堆尾元素ptrheap->size--; //删除堆尾元素AdjustDown(ptrheap->arry, ptrheap->size, 0); //将堆顶元素进行向下调整以保持堆的数据结构 }注意:AdjustDown接口的传参中,ptrheadp->size指的是堆元素的总个数,由于我们要将堆顶元素向下调整,因此传入的被调整结点编号为0
该接口每调用一次就可以删除一个堆顶数据(并保持小根堆的数据结构):
7.堆元素删除接口测试
我们先6次调用HeapPush接口创建一个六个元素的小堆,然后再6次调用HeapPop接口逐个删除堆顶元素(每删除一个堆顶数据打印一次堆,借此观察每次删除堆顶数据后堆的数据结构).
int main () {HP hp;HeapInit(&hp);HeapPush(&hp, 1);HeapPush(&hp, 5);HeapPush(&hp, 0);HeapPush(&hp, 8);HeapPush(&hp, 3);HeapPush(&hp, 9);HeapPrint(&hp);HeapPop(&hp);HeapPrint(&hp);HeapPop(&hp);HeapPrint(&hp);HeapPop(&hp);HeapPrint(&hp);HeapPop(&hp);HeapPrint(&hp);HeapPop(&hp);HeapPrint(&hp);HeapDestroy(&hp);}
观察小根堆的数据结构(逻辑结构):
- 可见逐个删除堆顶数据的过程中小根堆的数据结构得到了保持
8.逐个删除堆顶数据过程的时间复杂度分析(删堆的时间复杂度分析)
假设现在有一个N个元素的小根堆,我们逐个删除堆顶数据直到将堆删空。
现在我们来分析这个过程的时间复杂度(我们同样将二叉树看成满二叉树来分析):
- 同样我们考虑的是时间复杂度最坏的情况:即每次调用堆元素删除接口后,被交换到堆顶的元素都沿着连通路径向下被调整到叶结点
- 分析:假设堆的高度为h,则满树的总结点个数N为 : 2^h - 1
需要注意的是满树的第h层(最后一层)的结点个数为: 2^(h-1)所以满树的最后一层的结点个数占树的总结点个数的一半
因此如果我们删去满树的前h-1层的所有结点,则由最后一层结点所构成的新树的高度大致为h-1:
这也就意味着,在删除前h-1层结点的过程中树的总高度几乎不会发生变化:
因此可以得到删除满树的前h-1层所有结点过程中,每个被交换到堆顶的元素都要被向下调整log(N+1)次,则删除满树的前h-1层所有结点过程中,向下调整算法中循环语句执行总次数约为:
接着,对于由原树的最后一层(第h层)结点构成的新树(层数为h-1层)我们可以作类似的分析(即先删除其前h-2层结点,得到由其第h-1层结点构成的新树),以这种方式递推下去直到树被删空为止:
- 由此可得, 逐个删除堆顶数据直到将堆删空过程中,堆元素的向下调整算法中循环语句总的执行次数估算为:
该多项式的和化为大O阶渐进表示法结果为O(NlogN).
- 逐个删除堆顶数据直到将堆删空的过程的时间复杂度分析为:O(NlogN)
9.堆的实现代码总览(以小根堆为例)
接口和结构类型声明的头文件:
#pragma once #include <stdio.h> #include <assert.h> #include <stdlib.h> #include <stdbool.h> #include <time.h>//实现小堆typedef int HPDataType; typedef struct Heap {HPDataType* arry;size_t size;size_t capacity; }HP;//堆的初始化接口 void HeapInit(HP* php); //销毁堆的接口 void HeapDestroy(HP* php); //堆的打印接口 void HeapPrint(HP* php); //判断堆是否为空的接口 bool HeapEmpty(HP* php); //返回堆元素个数的接口 size_t HeapSize(HP* php); //返回堆顶元素的接口 HPDataType HeapTop(HP* php);void Swap(HPDataType* pa, HPDataType* pb); //堆元素向上调整算法接口 void AdjustUp(HPDataType* a, size_t child); //堆元素向下调整算法接口 void AdjustDown(HPDataType* a, size_t size,size_t parent); // 插入元素x以后,保持数据结构是(大/小)堆 void HeapPush(HP* php, HPDataType x); // 删除堆顶的数据后,保持数据结构是(大/小)堆 void HeapPop(HP* php);各个堆操作接口的实现:
#include "heap.h"//堆的初始化接口 void HeapInit(HP* ptrheap) {assert(ptrheap);ptrheap->arry = NULL;ptrheap->capacity = 0;ptrheap->size = 0;} //销毁堆的接口 void HeapDestroy(HP* ptrheap) {assert(ptrheap);free(ptrheap->arry);ptrheap->arry = NULL;ptrheap->capacity = 0;ptrheap->size = 0; }//堆的打印接口 void HeapPrint(HP* ptrheap) {assert(ptrheap);size_t tem = 0;for (tem = 0; tem < ptrheap->size; ++tem){printf("%d->", ptrheap->arry[tem]);}printf("END\n"); }//判断堆是否为空的接口 bool HeapEmpty(HP* ptrheap) {assert(ptrheap);return (0 == ptrheap->size); }//返回堆元素个数的接口 size_t HeapSize(HP* ptrheap) {assert(ptrheap);return ptrheap->size; }//返回堆顶元素的接口 HPDataType HeapTop(HP* ptrheap) {assert(!HeapEmpty(ptrheap));return ptrheap->arry[0]; }//元素交换接口 void Swap(HPDataType* e1, HPDataType* e2) {assert(e1 && e2);HPDataType tem = *e1;*e1 = *e2;*e2 = tem; }//小堆元素的向上调整接口 void AdjustUp(HPDataType* arry, size_t child) //child表示孩子结点的编号 {assert(arry);size_t parent = (child - 1) / 2;while (child > 0) //child减小到0时则调整结束{if (arry[child] < arry[parent]) //父结点大于子结点,则子结点需要上调以保持小堆的结构{Swap(arry + child, arry+parent);child = parent; //将原父结点作为新的子结点继续迭代过程parent = (child - 1) / 2; //继续向上找另外一个父结点}else{break; //父结点不大于子结点,则堆结构任然成立,无需调整}} }// 插入一个小堆元素的接口 // 插入x以后,保持其数据结构依旧是小堆 void HeapPush(HP* ptrheap, HPDataType x) {assert(ptrheap);if (ptrheap->capacity == ptrheap->size) //容量检查,容量不够则扩容{size_t newcapacity = (0 == ptrheap->capacity) ? 4 : 2 * ptrheap->capacity;HPDataType* tem = (HPDataType*)realloc(ptrheap->arry, newcapacity * sizeof(HPDataType));assert(tem);ptrheap->arry = tem;ptrheap->capacity = newcapacity;}ptrheap->arry[ptrheap->size] = x; //先尾插一个元素ptrheap->size++;//将尾插的元素进行向上调整以保持堆的数据结构AdjustUp(ptrheap->arry, ptrheap->size - 1); //根据完全二叉树的结构特点可知尾插进数组的元素在二叉树中编号为size-1 }//小堆元素的向下调整接口 void AdjustDown(HPDataType* arry,size_t size,size_t parent) {assert(arry);size_t child = 2 * parent + 1; //确定父结点的左孩子的编号while (child < size) //child增加到大于或等于size时则调整结束{if (child + 1 < size && arry[child + 1] < arry[child]) //确定左右孩子中较小的孩子结点{++child;}if ( arry[child] < arry[parent])//父结点大于子结点,则子结点需要上调以保持小堆的结构{Swap(arry + parent, arry + child);parent = child; //将原子结点作为新的父结点继续迭代过程child = 2 * parent + 1; //继续向下找另外一个子结点}else{break; //父结点不大于子结点,则堆结构任然成立,无需调整}} }//删除堆顶元素 void HeapPop(HP* ptrheap) {assert(ptrheap);Swap(ptrheap->arry, ptrheap->arry + ptrheap->size - 1); //交换堆顶与堆尾元素ptrheap->size--; //删除堆尾元素AdjustDown(ptrheap->arry, ptrheap->size, 0); //将堆顶元素进行向下调整以保持堆的数据结构 }
我们只需将小根堆的堆元素上下调整算法接口中的子父结点值大小比较符号改为大于号即可实现大根堆
10.结语
- 本文的核心:通过堆元素的上下调整算法接口完成堆的构建和删空(并分析过程的时间复杂度)
- 堆元素上下调整算法接口在后续的堆排序和TopK问题中还会直接用到
- 堆的高效性来源于如下数学思想:利用指数级展开的数据结构模型实现对数级回溯,从而降低了排序和查找的时间复杂度(不得不说前人的创造真的是无可比拟)

相关文章:

数据结构:堆的实现与建堆时间复杂度分析
目录 前言 一.堆的介绍 1.堆的本质 2.堆的分类 二.堆的实现(以小根堆为例) 1.关于二叉树的两组重要结论: 2.堆的物理存储结构框架(动态数组的简单构建) 3. 堆元素插入接口(以小根堆为例) 堆尾元素向上调整的算法接口: 4.堆元素插入接口测试 5.堆元素插入…...
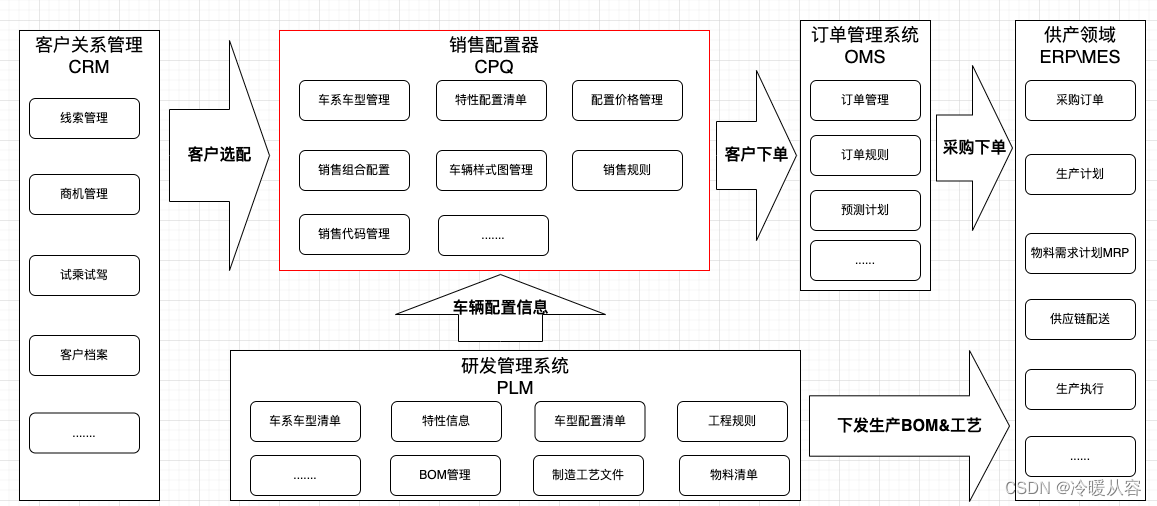
对“车辆销售配置器”的认识与理解
概述 中国汽车市场转为存量阶段后,各车企开始从”以产品为中心“转型到”以客户为中心“,产品的个性化配置需求日益丰富。随着竞争的加剧,车企们不仅要提供出色的产品,而且需要提供更加个性化的产品配置和服务,例如&am…...
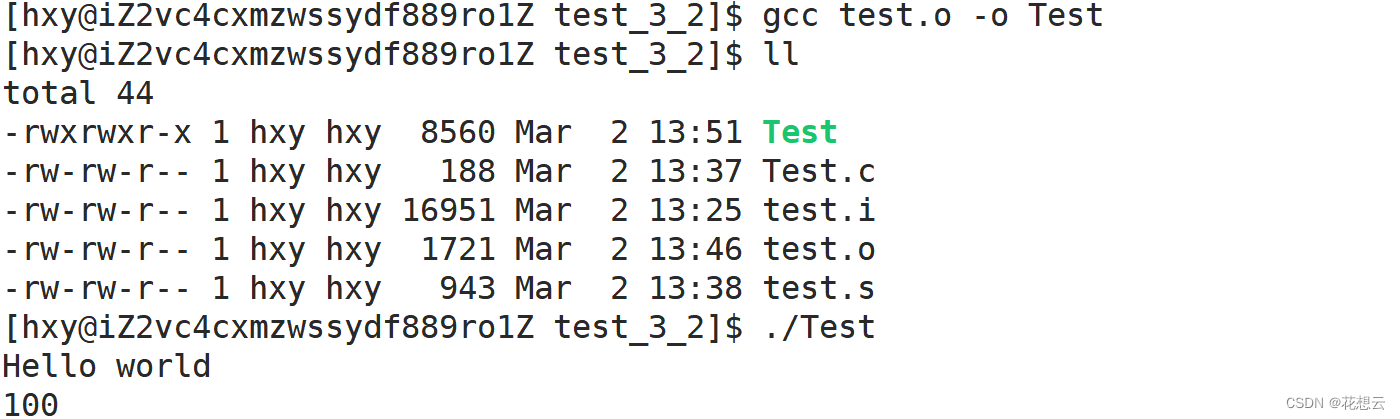
Linux编译器——gcc/g++(预处理、编译、汇编、链接)
目录 0.程序实现的两大环境 1.gcc如何完成 预处理 编译 汇编 链接 2.动态库与静态库 对比二者生成的文件大小 3. gcc常用选项 0.程序实现的两大环境 任何一个C程序的实现都要经过翻译环境与执行环境。 在翻译环境中又分为4个部分,预编译、编译、汇编与链…...

Java 操作图片进行缩放旋转翻转加水印
1 纯原生手写图片操作工具类 import java.awt.Dimension; import java.awt.Graphics2D; import java.awt.Image; import java.awt.Rectangle; import java.awt.image.BufferedImage; public class RotateImageUtil {public static BufferedImage rotateImage(BufferedImage bu…...

不能去演唱会现场就多听听耳机里的他们,教你用python来实现一个音乐播放器
前言 最近可以说大麦网很知名了,哈哈还有好多想要用Python来搞抢票脚本的 怎么说呢也不是不行,但是咱今天可不是来搞这个的,我可不抢票,抢了都去不了,上班搞钱啊铁铁们 咱就是说去不了现场,就多听听手机…...

CLion Debug 调试 Makefile 构建的 C 语言程序断点不起作用
最近在研究 jattach,打算在本地调试项目,发现 CLion 可以正常编译运行代码,却无法断点 Debug。由于笔者对 C/C 项目不熟悉,在此记录研究过程中遇到的一些基本问题与解决方法。 文章目录解决方式尝试过的手段【未解决】找 Native D…...
·神经网络
目录11神经网络demo112神经网络demo213神经网络demo320tensorflow2.0 安装教程,所有安装工具(神经网络)21神经网络-线性回归- demo122神经网络-线性回归- demo228神经网络-多层感知- demo1目录11神经网络demo1 package com.example.xxx; import java.ut…...

【Java 多线程学习】
多线程学习多线程1. 并行与并发2.进程和线程3. *****多线程的实现方式3.1 继承Thread类的方式进行实现3.2 实现Runnable接口方式进行实现3.3 利用Callable和Future接口方式实现3.4 设置获取线程名字4.获得线程对象5.线程休眠6.线程调度[线程的优先级]7.后台线程/守护线程多线程…...

【计算机考研408】快速排序的趟数问题 + PAT 甲级 7-2 The Second Run of Quicksort
前言 该题还未加入PAT甲级题库中,可以通过购买2022年秋季甲级考试进行答题,纯考研题改编 快速排序 常考的知识点 快速排序是基于分治法快速排序是所有内部排序算法中平均性能最优的排序算法快速排序是一种不稳定的排序算法快速排序算法中,…...
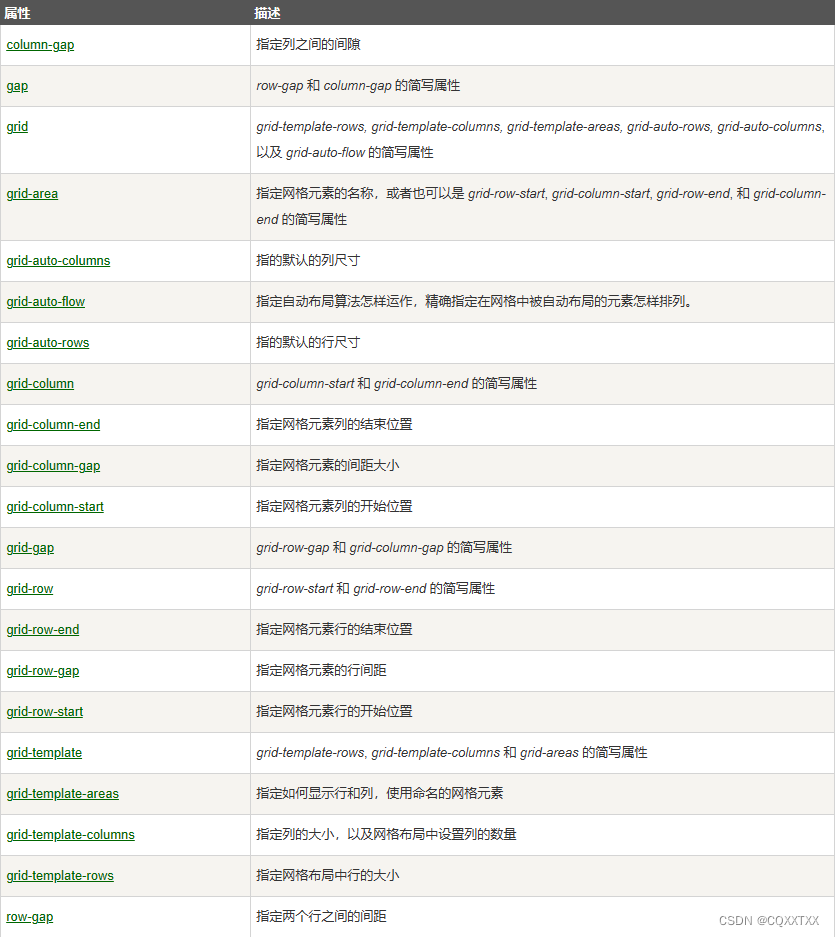
CSS-Grid(网格)布局
前言 之前HTML 页面的布局基本上都是通过 Flexbox 来实现的,能轻松的解决复杂的 Web 布局。 现在又出现了一个构建 HTML 最佳布局体系的新竞争者。就是强大的CSS Grid 布局。 grid和flex区别是什么?适用什么场景? Flexbox 是一维布局系统&am…...

软件测试4
一 form表单标签 1.form表单标签里面就是所有用户填写的表单数据; action“xxx.py”把表单数据提交给哪一个后台程序去处理 method“post” 传递数据时候的方式方法,post代表隐式提交数据、get明文传送数据 2.input标签的type类型 type“text” 普通的输…...

996的压力下,程序员还有时间做副业吗?
996怎么搞副业? 这个问题其实蛮奇怪的:996的压力下,怎么会还想着搞副业呢? 996还想搞副业的原因有哪些? 大家对于996应该都不陌生,总结就是一个字:忙。 996的工作性质就是加班,就…...

每日学术速递3.1
CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 Subjects: cs.CV 1.Directed Diffusion: Direct Control of Object Placement through Attention Guidance 标题:定向扩散:通过注意力引导直接控制物体放置 作者:…...
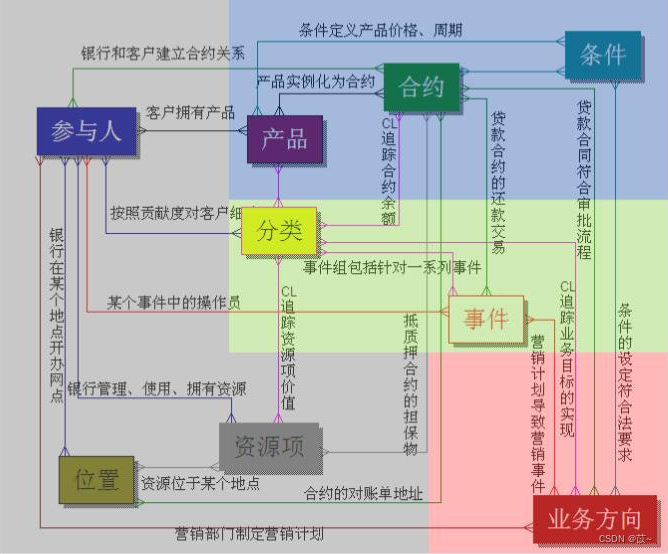
金融行业数据模型
一、Teradata FS-LDM Teradata 公司基于金融业务发布的FS-LDM(Financial Servies Logical Data Model) 十大主题:当事人、产品、协议、事件、资产、财务、机构、地域、营销、渠道。 1、当事人(Party) 银行所服务的任…...

【面试题】2023前端vue面试题及答案
Vue3.0 为什么要用 proxy?在 Vue2 中, 0bject.defineProperty 会改变原始数据,而 Proxy 是创建对象的虚拟表示,并提供 set 、get 和 deleteProperty 等处理器,这些处理器可在访问或修改原始对象上的属性时进行拦截&…...
leetcode128. 最长连续序列)
(哈希查找)leetcode128. 最长连续序列
文章目录一、题目1、题目描述2、基础框架3、原题链接二、解题报告1、思路分析2、时间复杂度3、代码详解三、本题小知识一、题目 1、题目描述 给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。…...

js中splice方法和slice方法
splice方法用来操作数组splice(startIndex,deleteNum,item1,....,)此操作会改变原数组。删除数组中元素参数解释:startIndex为起始index索引。deleteNum为从startIndex索引位置开始需要删除的个数。分三种情况:没有传第三个参数的情况下,dele…...

c++ argparse
需求 c程序传参数,像python中argparse一样方便。 方法1 用gflags 参考https://heroacool.blog.csdn.net/?typeblog git clone https://github.com/gflags/gflags cd gflags # 进入项目文件夹 cmake . # 使用 cmake 编译生成 Makefile 文件 make -j 24 # make 编…...

内大892复试真题16年
内大892复试真题16年 1. 输出三个数中较大数2. 求两个数最大公约数与最小公倍数3. 统计字符串中得字符个数4. 输出菱形5. 迭代法求平方根6. 处理字符串(逆序、进制转换)7. 寻找中位数8. 输入十进制输出n进制1. 输出三个数中较大数 问题 代码 #include <iostream>usin…...

面试题 05.02. 二进制数转字符串
二进制数转字符串。给定一个介于0和1之间的实数(如0.72),类型为double,打印它的二进制表达式。如果该数字无法精确地用32位以内的二进制表示,则打印“ERROR”。 示例1: 输入:0.625输出:"0…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...