当前位置： 首页 > news >正文

uniapp开发小程序经验记录

news 2026/2/8 2:15:59

uniapp开发小程序的过程中会遇到很多问题，这里记录一下相关工具优化，便于后来者参考。

每次保存代码后，小程序都跳回首页

针对这个问题，常规的做法就是修改pages配置文件，但是这种方式不便于路由参数的设置，而且每次都是编码级的调整。
因此推荐使用开发工具中提供的”编译模式进行指定，流程如下：

  1. 小程序模拟器界面点进正在修改的目标页面
  2. 在”普通编译“下拉框中选择”添加编译模式“
    在这里插入图片描述
  3. 这一步会弹出对话框表单，并自动将当前页面已传入的参数填充进表单。如无特殊配置，那么录入”模式名称“然后点击确定即可保存。
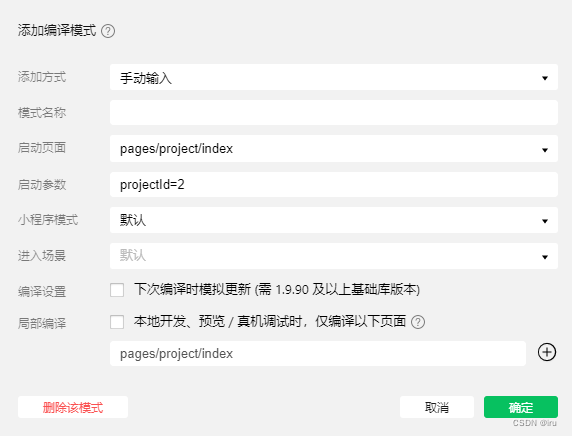
    在这里插入图片描述
    后续再修改代码，只要这里的编译模式切换为指定模式，即可以此页面及当前所设置的传参为首页。

设计稿没按750 宽的屏幕为基准

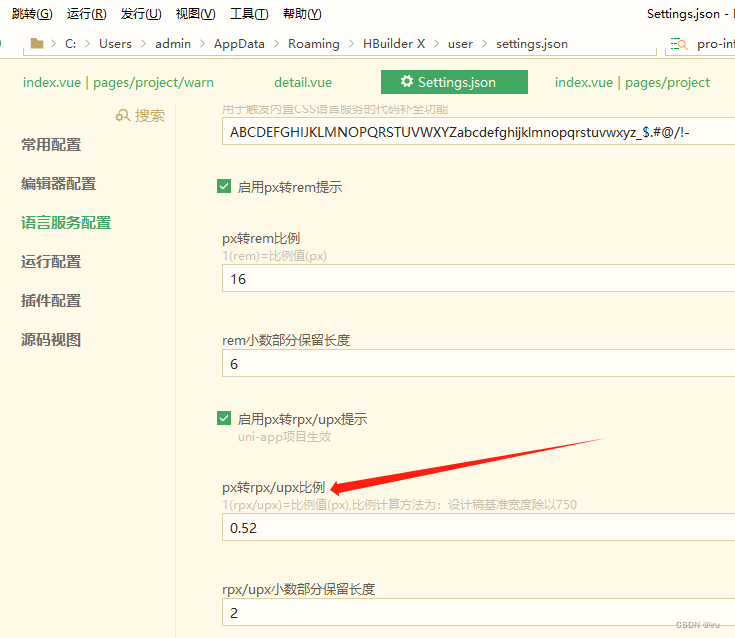
查看设计稿宽度基准值，使用基准值除以750，将值写入下方箭头所指向的位置。比如我的设计稿宽度是390，那么390 ÷ 750 = 0.52，因此我在此处填入值为0.52，保留小数点后两位。

操作入口：工具》设置》语言服务配置
在这里插入图片描述
设置后效果
在这里插入图片描述

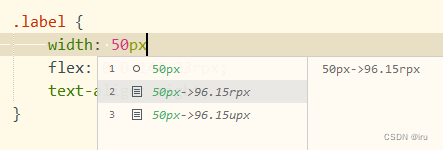
相关文章：

uniapp开发小程序经验记录

uniapp开发小程序的过程中会遇到很多问题，这里记录一下相关工具优化，便于后来者参考。 每次保存代码后，小程序都跳回首页 针对这个问题，常规的做法就是修改pages配置文件，但是这种方式不便于路由参数的设置&#xff…...

编程日记 2023/12/11 21:04:59

PR自动剪辑视频工具AI智能剪辑插件AutoPod

推荐一款可以提高剪辑效率，节约时间成本的AI人工智能自动剪辑视频制作工具pr插件Autopod，辅助你更快地完成视频内容的编辑工作。 Autopod 插件是一款应用于 Adobe Premiere Pro 软件的插件，用于自动剪辑。该插件能够识别和处理视频和音频素材…...

编程日记 2023/12/11 20:59:55

Visual Studio 2022+Python3.11实现C++调用python接口

大家好！我是编码小哥，欢迎关注，持续分享更多实用的编程经验和开发技巧，共同进步。 查了一些资料，不是报这个错，就是报哪个错，没有找到和我安装的环境的一致的案例，于是将自己的摸索分…...

编程日记 2023/12/11 20:57:54

10天玩转Python第2天：python判断语句基础示例全面详解与代码练习

目录 1.课程之前1.1 复习和反馈1.2 作业1.3 今日内容1.4 字符串格式化的补充1.5 运算符1.5.1 逻辑运算符1.5.2 赋值运算符1.5.3 运算符优先 2.判断2.1 if 的基本结构2.1.1 基本语法2.1.2 代码案例2.1.3 练习 2.2 if else 结构2.2.1 基本语法2.2.2 代码案例2.2.3 练习 2.3 if 和…...

编程日记 2023/12/11 20:56:53

2024年网络安全竞赛-网站渗透

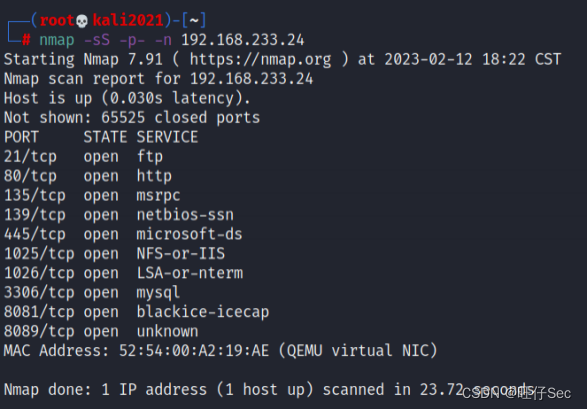
网站渗透 （一）拓扑图 1.使用渗透机对服务器信息收集，并将服务器中网站服务端口号作为flag提交； 使用nmap工具对靶机进行信息收集 2.使用渗透机对服务器信息收集，将网站的名称作为flag提交； 访问页面即可 3.使用渗透机对服务器渗透，将可渗透页面的名称作为flag提交…...

编程日记 2023/12/11 20:55:52

kafka学习笔记--基础知识概述

本文内容来自尚硅谷B站公开教学视频，仅做个人总结、学习、复习使用，任何对此文章的引用，应当说明源出处为尚硅谷，不得用于商业用途。 如有侵权、联系速删 视频教程链接：【尚硅谷】Kafka3.x教程（从入门到调优…...

编程日记 2023/12/11 20:54:51

聊聊AsyncHttpClient的KeepAliveStrategy

序 本文主要研究一下AsyncHttpClient的KeepAliveStrategy KeepAliveStrategy org/asynchttpclient/channel/KeepAliveStrategy.java public interface KeepAliveStrategy {/*** Determines whether the connection should be kept alive after this HTTP message exchange.…...

编程日记 2023/12/11 20:53:50

视频推拉流直播点播EasyDSS平台点播文件加密存储的实现方法

视频推拉流直播点播系统EasyDSS平台，可提供流畅的视频直播、点播、视频推拉流、转码、管理、分发、录像、检索、时移回看等功能，可兼容多操作系统，还能支持CDN转推，具备较强的可拓展性与灵活性，在直播点播领域具有广泛…...

编程日记 2023/12/11 20:52:49

LVGL——按钮部件

目录 一、组成部分 二、按钮部件操作 1、创建 2、设置样式 3、添加事件 4、代码例程 三、按钮部件案例 一、组成部分 主体（LV_PART_MAIN） 二、按钮部件操作 1、创建 lv_obj_t *btn lv_btn_create( parent );2、设置样式 lv_obj_set_siz…...

编程日记 2023/12/11 20:51:47

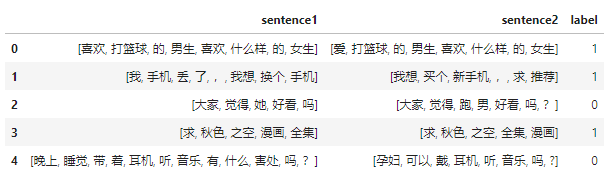
RE2文本匹配调优实战

引言 在RE2文本匹配实战的最后，博主说过会结合词向量以及其他技巧来对效果进行调优，本篇文章对整个过程进行详细记录。其他文本匹配系列实战后续也会进行类似的调优，方法是一样的，不再赘述。 本文所用到的词向量可以在Gensim训练…...

编程日记 2023/12/11 20:50:46

Java - 线程间的通信方式

线程通信的方式 线程中通信是指多个线程之间通过某种机制进行协调和交互 线程通信主要可以分为三种方式，分别为共享内存、消息传递和管道流。每种方式有不同的方法来实现 共享内存：线程之间共享程序的公共状态，线程之间通过读-写内存中的公…...

编程日记 2023/12/11 20:48:45

【计算机网络】HTTP响应报文Cookie原理

目录 HTTP响应报文格式 一. 状态行 状态码与状态码描述 二. 响应头 Cookie原理 一. 前因 二. Cookie的状态管理 结束语 HTTP响应报文格式 HTTP响应报文分为四部分 状态行：包含三部分：协议版本，状态码，状态码描述响应头&a…...

编程日记 2023/12/11 20:47:44

2023年度盘点：智能汽车、自动驾驶、车联网必读书单

【文末送书】今天推荐几本自动驾驶领域优质书籍 前言 2023年，智能驾驶和新能源汽车行业仍然有着肉眼可见的新进展。自动驾驶技术继续尝试从辅助驾驶向自动驾驶的过渡，更重要的是相关技术成本的下降。根据《全球电动汽车展望2023》等行业报告&#xff0c…...

编程日记 2023/12/11 20:46:43

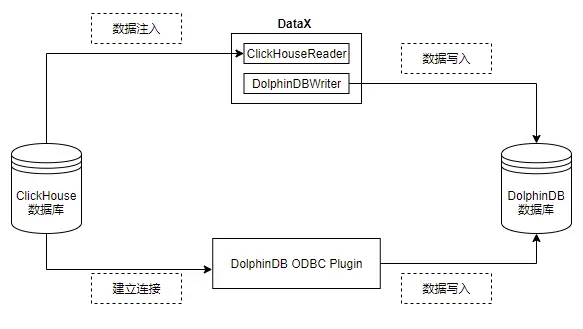
一文讲解如何从 Clickhouse 迁移数据至 DolphinDB

ClickHouse 是 Yandex 公司于2016年开源的 OLAP 列式数据库管理系统，主要用于 WEB 流量分析。凭借面向列式存储、支持数据压缩、完备的 DBMS 功能、多核心并行处理的特点，ClickHouse 被广泛应用于广告流量、移动分析、网站分析等领域。 DolphinDB 是一款…...

编程日记 2023/12/11 20:45:42

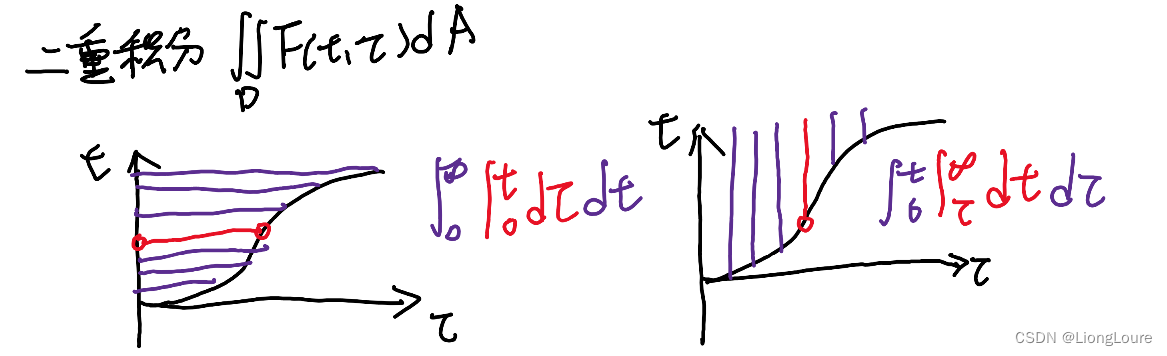
[足式机器人]Part2 Dr. CAN学习笔记-数学基础Ch0-5Laplace Transform of Convolution卷积的拉普拉斯变换

本文仅供学习使用 本文参考： B站：DR_CAN Dr. CAN学习笔记-数学基础Ch0-5Laplace Transform of Convolution卷积的拉普拉斯变换 Laplace Transform : X ( s ) L [ x ( t ) ] ∫ 0 ∞ x ( t ) e − s t d t X\left( s \right) \mathcal{L} \left[ x\lef…...

编程日记 2023/12/11 20:43:40

生产问题: 利用线程Thread预加载数据缓存,其它类全局变量获取缓存偶发加载不到

生产问题: 利用线程Thread预加载数据缓存偶发加载不到 先上代码 public class ThreadTest {//本地缓存Map<String, Object> map new HashMap<String, Object>();class ThreadA implements Runnable{Overridepublic void run() {System.out.println("Thread…...

编程日记 2023/12/11 20:41:38

Elasticsearch mapping 之 性能相关配置

ES 常见类型 通用类型: 二进制: binary 布尔型: boolean 字符串: keyword, constant_keyword, wildcard, text 别名: alias 对象: object, flattened, nested, join 结构化数据类型: Range, ip, version, murmur3 空间数据类型: geo_point, geo_shape, point, shape 性…...

编程日记 2023/12/11 20:39:36

adb push报错：remote couldn‘t create file: Is a directory

adb push报错&#xff1a;remote couldn‘t create file: Is a directory 出现这个问题可能是电脑本地目录中包含中文或者是目录地址中多包含了一个/ 比如说以下两种路径 1. test/测试音频文件1/a.mp3 2.test/test_audio/ 这两种都是不可以的&#xff08;我是在as中执行的…...

编程日记 2023/12/11 20:37:34

GitLab 服务更换了机器，IP 地址或域名没有变化时，可能会出现无法拉取或提交代码的情况。

当 GitLab 服务更换了机器&#xff0c;但 IP 地址或域名没有变化时&#xff0c;可能会出现无法拉取或提交代码的情况。 这可能是由于 SSH 密钥或 SSL 证书发生了变化。以下是一些可能的解决步骤&#xff1a; 这可能是由于 SSH 密钥或 SSL 证书发生了变化。以下是一些可能的解决…...

编程日记 2023/12/11 20:34:32

【华为OD题库-076】执行时长/GPU算力-Java

题目 为了充分发挥GPU算力&#xff0c;需要尽可能多的将任务交给GPU执行&#xff0c;现在有一个任务数组&#xff0c;数组元素表示在这1秒内新增的任务个数且每秒都有新增任务。 假设GPU最多一次执行n个任务&#xff0c;一次执行耗时1秒&#xff0c;在保证GPU不空闲情况下&…...

编程日记 2023/12/11 20:29:28

RocketMQ延迟消息机制

两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数&#xff0c;对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后&#xf…...

编程新知 2026/2/5 5:03:16

Day131 | 灵神 | 回溯算法 | 子集型 子集

Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣&#xff08;LeetCode&#xff09; 思路&#xff1a; 笔者写过很多次这道题了&#xff0c;不想写题解了&#xff0c;大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

编程新知 2026/1/23 12:37:51

深入理解JavaScript设计模式之单例模式

目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式&#xff08;Singleton Pattern&#…...

编程新知 2026/1/31 17:09:43

在四层代理中还原真实客户端ngx_stream_realip_module

一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡&#xff08;如 HAProxy、AWS NLB、阿里 SLB&#xff09;发起上游连接时&#xff0c;将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后&#xff0c;ngx_stream_realip_module 从中提取原始信息…...

编程新知 2026/1/4 5:02:00

MODBUS TCP转CANopen 技术赋能高效协同作业

在现代工业自动化领域&#xff0c;MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步&#xff0c;这两种通讯协议也正在被逐步融合&#xff0c;形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

编程新知 2026/2/6 9:48:02

GitHub 趋势日报 (2025年06月08日)

&#x1f4ca; 由 TrendForge 系统生成 | &#x1f310; https://trendforge.devlive.org/ &#x1f310; 本日报中的项目描述已自动翻译为中文 &#x1f4c8; 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

编程新知 2025/12/13 1:32:15

springboot整合VUE之在线教育管理系统简介

可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生&#xff0c;小白用户&#xff0c;想学习知识的 有点基础&#xff0c;想要通过项…...

编程新知 2026/1/26 9:30:45

【p2p、分布式，区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制

目录 节点的功能承载层&#xff08;GATT/Adv&#xff09;局限性&#xff1a; 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能&#xff0c;如 Configuration …...

编程新知 2026/2/4 22:41:52

华为OD机试-最短木板长度-二分法(A卷,100分)

此题是一个最大化最小值的典型例题&#xff0c; 因为搜索范围是有界的&#xff0c;上界最大木板长度补充的全部木料长度&#xff0c;下界最小木板长度&#xff1b; 即left0,right10^6; 我们可以设置一个候选值x(mid)&#xff0c;将木板的长度全部都补充到x&#xff0c;如果成功…...

编程新知 2026/2/4 17:42:50

机器学习的数学基础：线性模型

线性模型 线性模型的基本形式为&#xff1a; f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法&#xff0c;得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

编程新知 2025/10/2 9:07:50