大话数据结构-栈
1 概述
栈(Stack)是限定仅在表尾进行插入和删除操作的线性表。
允许插入和删除的一端称为栈顶(top),另一端称为栈底(bottom),不含任何数据元素的栈称为空栈,栈又称为后进先出(Last In First Out)的线性表,简称LIFO结构。
栈的插入操作,叫作进栈,也称压栈、入栈;栈的删除操作,叫作出栈,也有的叫作弹栈。
2 栈的抽象数据类型
ADT 栈(Stack)Data:同线性表。元素具有相同的类型,相邻元素具有前驱和后继关系。Operation:init(int maxSize):初始化操作,建立一个空栈;destroy():若栈存在,则销毁它;clear():清空栈;isEmpty():若栈为空,返回true,否则返回false;getTop():若栈存在且非空,则返回栈顶元素;push(DataType e):进栈;pop():出栈;length():返回栈的元素个数;
endADT
3 顺序存储结构
3.1 概述
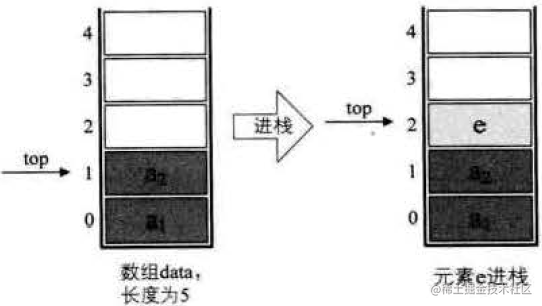
基于栈的特殊性,我们可以考虑使用数组来实现栈,令数组的下标为0的元素作为栈底元素,并定义一个top指针来指向栈顶元素在数组中的位置:

3.2 进栈操作
把数据添加到top指向的下标的下一个下标,然后把top下移一位即可:
代码实现如下:
/*** 进栈操作** @param value 待进栈的值* @throws RuntimeException 栈满时抛出* @author Korbin* @date 2023-01-10 11:32:41**/
public void push(T value) {if (top == maxSize - 1) {throw new RuntimeException("fulled");}data[++top] = value;
}
3.3 出栈操作
返回top所在的当前元素,并令top减1即可:
/*** 出栈** @return 出栈的元素* @throws RuntimeException 栈空时抛出异常* @author Korbin* @date 2023-01-10 11:34:49**/
public T pop() {if (top == -1) {throw new RuntimeException("empty stack");}return data[top--];
}
3.4 完整代码
import java.util.Arrays;/*** 栈* <p>* 线性栈顶的数据为一个数组,数组的第一个元素(索引为0)为栈底* <p>* 栈是先进后出的数据结构** @author Korbin* @date 2023-01-10 11:21:07**/
public class Stack<T> {/*** 栈内数据**/private T[] data;/*** 栈的最大长度**/private int maxSize;/*** 栈顶指针,为数组索引* <p>* 值为-1时表示空栈**/private int top = -1;/*** 清空栈**/public void clear() {init(maxSize);}/*** 获取栈顶指针** @return 栈顶指针* @author Korbin* @date 2023-01-10 11:45:08**/public T getTop() {if (top == -1) {throw new RuntimeException("empty stack");}return data[top];}/*** 初始化** @param maxSize 栈的长度* @author Korbin* @date 2023-01-10 11:38:41**/@SuppressWarnings("unchecked")public void init(int maxSize) {this.maxSize = maxSize;data = (T[]) new Object[maxSize];top = -1;}/*** 栈是否为空栈,空栈返回true,否则返回false* <p>* top为-1时为空栈**/public boolean isEmpty() {return top == -1;}/*** 栈的元素个数**/public int length() {return top + 1;}/*** 出栈** @return 出栈的元素* @throws RuntimeException 栈空时抛出异常* @author Korbin* @date 2023-01-10 11:34:49**/public T pop() {if (top == -1) {throw new RuntimeException("empty stack");}return data[top--];}/*** 进栈操作** @param value 待进栈的值* @throws RuntimeException 栈满时抛出* @author Korbin* @date 2023-01-10 11:32:41**/public void push(T value) {if (top == maxSize - 1) {throw new RuntimeException("fulled");}data[++top] = value;}@Overridepublic String toString() {return "Stack{" + "data=" + Arrays.toString(data) + ", stackSize=" + maxSize + ", top=" + top + '}';}}
4 两栈共享空间
4.1 概述
顺序存储的栈使用数组存储数据,将下标为0的元素作为栈底元素,并定义了top指向栈顶元素,定义maxSize确认栈中最大可以存储的元素个数。
这种实现方式可能造成maxSize定义较大,但实际使用的空间较小的情况,因此为了尽可能节省或者说尽可能利用上存储空间,如果有两个栈是相同的数据类型时,可以将两个栈一起放置在一个数组中,栈A以下标为0的元素为栈底,栈B以下标为maxSize-1的元素为栈底,双向进行操作,以最大利用定义好的数组空间。

实现方式并不复杂,只是由原来的只管理一个top,变成管理两个top,只要top1和top2不“见面”,那么数组就可以一直被使用,因此,当top1 + 1 = top2时,才表示栈满了,这时,两个top“见面”了。
4.2 代码实现
import java.util.Arrays;/*** 双向顺序栈* <p>* 一个数组中包含两个栈,栈1的栈顶索引为0,栈2的栈顶索引为n-1* <p>* 当栈1的栈顶索引为-1时,表示栈1为空栈* <p>* 当栈2的栈顶索引为n时,表示栈2为空栈** @author Korbin* @date 2023-01-10 11:54:20**/
public class BidirectionalStack<T> {/*** 栈内数据**/private T[] data;/*** 栈的最大长度**/private int maxSize;/*** 栈1的栈顶指针,为数组索引* <p>* 值为-1时表示空栈**/private int top1 = -1;/*** 栈2的栈顶指针,为数组索引* <p>* 值为stackSize时表示空栈**/private int top2 = -1;/*** 清空栈** @param stackNumber 栈的数量,只能为1或2* @throws RuntimeException 当栈为空或stackNumber不为1和2时抛出异常* @author Korbin* @date 2023-01-16 10:14:32**/public void clear(int stackNumber) {if (stackNumber == 1) {for (int i = 0; i <= top1; i++) {data[i] = null;}top1 = -1;} else if (stackNumber == 2) {for (int i = maxSize - 1; i >= top2; i--) {data[i] = null;}top2 = maxSize;} else {throw new RuntimeException("error stack number");}}/*** 获取栈1的栈顶指针** @param stackNumber 栈的数量,只能为1或2* @return 栈顶指针* @throws RuntimeException 当栈为空或stackNumber不为1和2时抛出异常* @author Korbin* @date 2023-01-10 11:45:08**/public T getTop(int stackNumber) {if (stackNumber == 1) {if (top1 == -1) {throw new RuntimeException("empty stack");}return data[top1];} else if (stackNumber == 2) {if (top2 == maxSize) {throw new RuntimeException("empty stack");}return data[top2];} else {throw new RuntimeException("error stack number");}}/*** 初始化** @param maxSize 栈的长度* @author Korbin* @date 2023-01-10 11:38:41**/@SuppressWarnings("unchecked")public void init(int maxSize) {this.maxSize = maxSize;this.top1 = -1;this.top2 = maxSize;data = (T[]) new Object[maxSize];}/*** 栈是否为空** @param stackNumber 栈的数量,只能为1或2* @return 为空返回true,不为空返回false* @throws RuntimeException 当栈为空或stackNumber不为1和2时抛出异常* @author Korbin* @date 2023-01-16 10:16:29**/public boolean isEmpty(int stackNumber) {if (stackNumber == 1) {return top1 == -1;} else if (stackNumber == 2) {return top2 == maxSize;} else {throw new RuntimeException("error stack number");}}/*** 返回栈的元素个数** @param stackNumber 栈的数量,只能为1或2* @return 栈的元素个数* @throws RuntimeException 当栈为空或stackNumber不为1和2时抛出异常* @author Korbin* @date 2023-01-16 10:18:19**/public int length(int stackNumber) {if (stackNumber == 1) {return top1 + 1;} else if (stackNumber == 2) {return maxSize - top2;} else {throw new RuntimeException("error stack number");}}/*** 出栈** @param stackNumber 栈的数量,只能为1或2* @return 出栈的值* @throws RuntimeException 当栈为空或stackNumber不为1和2时抛出异常* @author Korbin* @date 2023-01-10 12:06:56**/public T pop(int stackNumber) {if (stackNumber == 1) {// 栈1出栈if (top1 == -1) {throw new RuntimeException("empty stack");}T result = data[top1];data[top1] = null;top1--;return result;} else if (stackNumber == 2) {// 栈2出栈if (top2 == maxSize) {throw new RuntimeException("empty stack");}T result = data[top2];data[top2] = null;top2++;return result;} else {throw new RuntimeException("error stack number");}}/*** 进栈** @param value 待进栈的值* @param stackNumber 栈的数量,为1或2* @throws RuntimeException 栈满或者stackNumber不为1和2时抛出异常* @author Korbin* @date 2023-01-10 12:03:48**/public void push(T value, int stackNumber) {if (top1 + 1 == top2) {throw new RuntimeException("fulled");}if (stackNumber == 1) {// 栈1进栈data[++top1] = value;} else if (stackNumber == 2) {// 栈2进栈data[--top2] = value;} else {throw new RuntimeException("error stack number");}}@Overridepublic String toString() {return "BidirectionalStack{" + "data=" + Arrays.toString(data) + ", stackSize=" + maxSize + ", top1=" + top1 +", top2=" + top2 + '}';}}
5 栈的链式存储结构
5.1 概述
栈的链式存储结构,简称为链栈,处理方式是,把栈顶放在单链表的头部,用来代替头结点:

栈的结点定义中,用data表示存储的元素,用next表示后继节点:
import lombok.Data;/*** 链栈节点** @author Korbin* @date 2023-01-10 17:12:00**/
@Data
public class StackNode<T> {/*** 节点值**/private T data;/*** 后继节点**/private StackNode<T> next;}
5.2 进栈操作
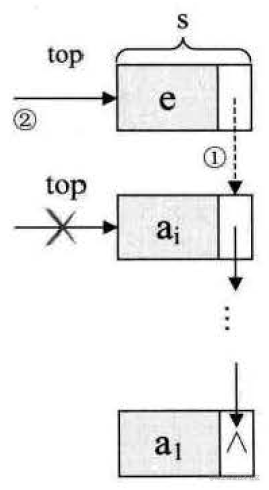
链栈中定义了两个属性,一为top,指向栈顶元素,一为count,表示的是实际元素的数量。
因此链栈在进栈时,只需要两步操作:
(1) 定义一个新的结点,令其的后继结点指向top结点;
(2) 令top指向新定义的结点;
/*** 进栈** @param value 待进栈的节点值* @author Korbin* @date 2023-01-10 17:31:45**/
public void push(T value) {StackNode<T> newNode = new StackNode<>();newNode.setData(value);newNode.setNext(top);top = newNode;count++;
}
5.3 出栈操作
令top指向其后继结点即可:
/*** 出栈** @return 出栈的节点* @throws RuntimeException 栈为空时抛出异常* @author Korbin* @date 2023-01-10 17:38:10**/
public StackNode<T> pop() {if (count == 0) {throw new RuntimeException("empty stack");}StackNode<T> result = top;top = top.getNext();count--;return result;
}
5.4 完整代码
/*** 链栈,即链式存储的栈** @author Korbin* @date 2023-01-10 17:21:26**/
public class LinkStack<T> {/*** 节点数量**/private int count = 0;/*** 栈顶指针**/private StackNode<T> top = null;/*** 清空链栈** @author Korbin* @date 2023-01-16 10:34:55**/public void clear() {init();}/*** 获取栈顶节点** @return 栈顶节点* @author Korbin* @date 2023-01-10 17:34:41**/public StackNode<T> getTop() {return top;}/*** 初始化链栈** @author Korbin* @date 2023-01-16 10:34:55**/public void init() {top = null;count = 0;}/*** 是否为空栈,是则返回true,否则返回false** @return 空栈返回true,否则返回false* @author Korbin* @date 2023-01-16 10:35:29**/public boolean isEmpty() {return count == 0;}/*** 获取总节点数** @return 总节点数* @author Korbin* @date 2023-01-10 17:32:14**/public int length() {return count;}/*** 出栈** @return 出栈的节点* @throws RuntimeException 栈为空时抛出异常* @author Korbin* @date 2023-01-10 17:38:10**/public StackNode<T> pop() {if (count == 0) {throw new RuntimeException("empty stack");}StackNode<T> result = top;top = top.getNext();count--;return result;}/*** 进栈** @param value 待进栈的节点值* @author Korbin* @date 2023-01-10 17:31:45**/public void push(T value) {StackNode<T> newNode = new StackNode<>();newNode.setData(value);newNode.setNext(top);top = newNode;count++;}@Overridepublic String toString() {StringBuilder builder = new StringBuilder("[");if (null != top) {StackNode<T> tmp = top;builder.append(tmp.getData()).append(",");while (null != tmp.getNext()) {builder.append(tmp.getNext().getData()).append(",");tmp = tmp.getNext();}}builder.append("]");return builder.toString();}}
BTW:用Java来描述数据结构可能不是一个好的方式——所有内存的处理都忽略了——也可能是我还学不到家。
6 栈的应用-四则运算表达式求值
6.1 中缀表示法、前缀表示法、后缀表示法
通常我们看到的四则运算,称为中缀表示法比如:
a + b * c - (d + e)
前缀表示法又称波兰表示法,即把运算符放在前面,操作数写在后面,前缀表示法是一种没有括号的表示法,将中缀表示法转化成前缀表示法的步骤为:
(1) 首先按照运算符的优先级对所有的运算单位加括号;
(2) 转前缀则将符号移动到对应括号之前;
(3) 去掉括号;
如上述表达式,我们先将所有运算单位加上括号,我们知道,上述表达式的运算过程应为:
(1) 计算d + e;
(2) 计算b * c;
(3) 计算a + (b * c);
(4) 计算(a + (b * c)) - (d + e);
因此,把所有运算单元都加上括号后,表达式变为:
((a + (b * c)) - ( d + e ))
注意,每一步都要加上括号。
然后,我们把每个运算符,都移到到其对应的括号前面,表达式变成:
-(+(a *(b c)) +( d e ))
再把括号省略掉,得到前缀表达式:
- + a * b c + d e
后缀表达式转换方式类似,先加括号:
((a + (b * c)) - ( d + e ))
然后把运算符移到对应括号后面:
((a (b c)*)+ ( d e )+)-
然后去掉括号,得到结果:
a b c * + d e + -
6.2 中缀表达式转前缀表达式的代码实现
代码实现时与手动算法不同,遵循如下过程:
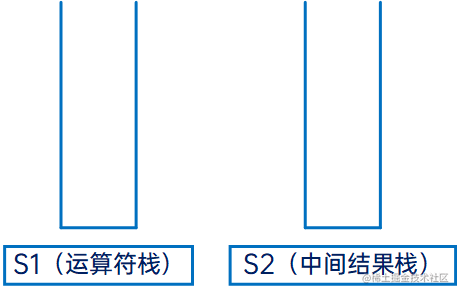
(1) 初始化两个栈:运算符栈S1和储存中间结果的栈S2;
(2) 从右至左扫描中缀表达式;
(3) 遇到操作数时,将其压入S2;
(4) 遇到运算符时,比较其与S1栈顶运算符的优先级:
1) 如果S1为空,或栈顶运算符为右括号“)”,则直接将此运算符入栈;
2) 否则,若优先级比栈顶运算符的较高或相等,也将运算符压入S1;
3) 否则,将S1栈顶的运算符弹出并压入到S2中,然后从S1中取出栈顶元素,再将待处理的元素与栈顶运行符比较,处理方式与第(4)点相同;
(5) 遇到括号时:
1) 如果是右括号“)”,则直接压入S1;
2) 如果是左括号“(”,则依次弹出S1栈顶的运算符,并压入S2,直到遇到右括号为止,此时将这一对括号丢弃;
(6) 重复步骤(2)至(5),直到表达式的最左边;
(7) 将S1中剩余的运算符依次弹出并压入S2;
(8) 依次弹出S2中的元素并输出,结果即为中缀表达式对应的前缀表达式。
以以下表达式为例:
a + b * c - (d + e)
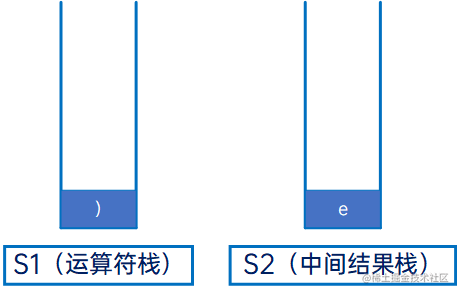
首先是两个空栈S1和S2:
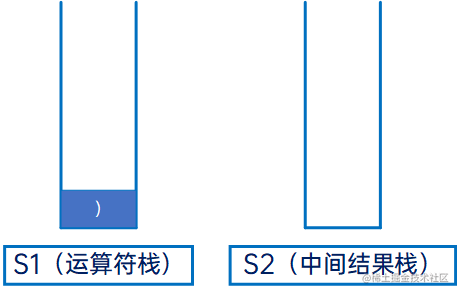
然后是倒序迭代给定的字符串,首先是“)”,右括号直接压入S1:
然后是“e”,操作数,直接压入S2:
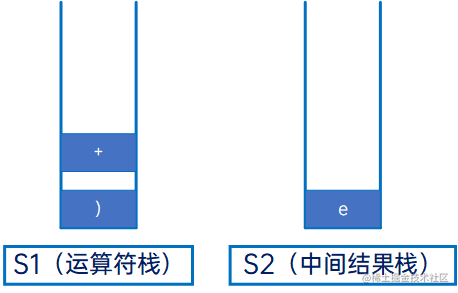
然后是“+”,运算符,与S1的栈顶元素“)”比较,直接入S1栈:
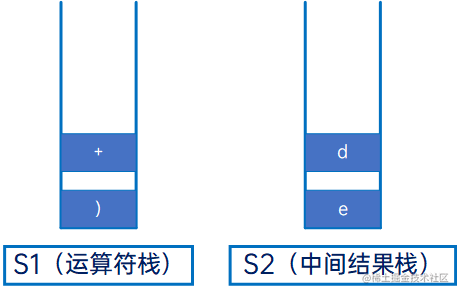
然后是“d”,操作数,直接压入S2:
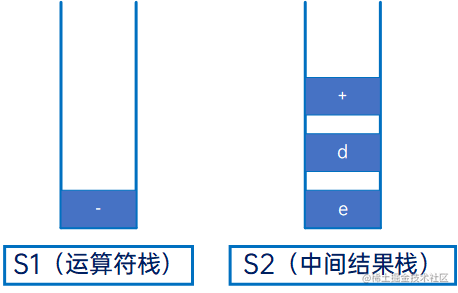
然后是“(”,依次弹出S1的栈顶元素,直到遇到“)”,并抛弃这一对括号:

然后是“-”,与S1的栈顶元素比较,因S1的栈顶元素是空,因此直接进入S1栈:
然后是“c”,操作数,直接压入S2:

然后是“*”,与S的栈顶元素“-”比较,优先级较高,因此压入S1:
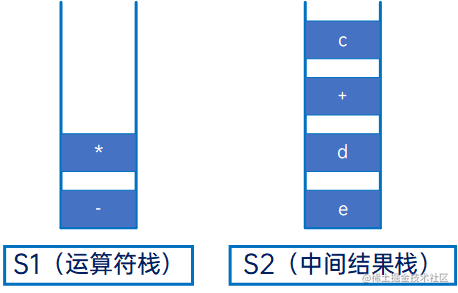
然后是“b”,操作数,直接压入S2:
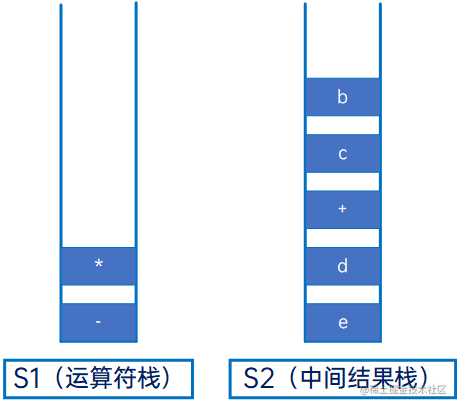
然后是“+”,与S1的栈顶元素“*”比较,优先级较低,因此先将S1的栈顶元素弹出,放到S2:
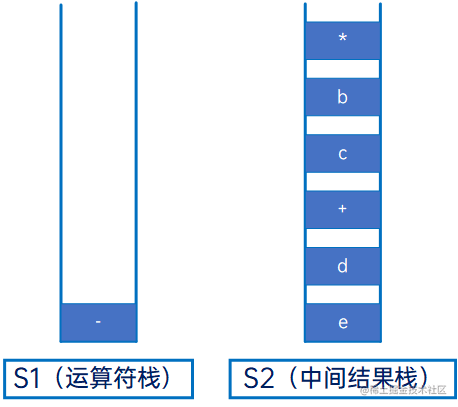
然后与S1新的栈顶元素“-”相比,优先级相同,因此直接将“+”压入S1:
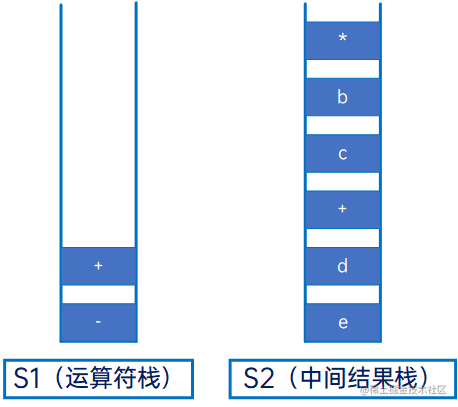
然后是“a”,操作数,直接压入S2:
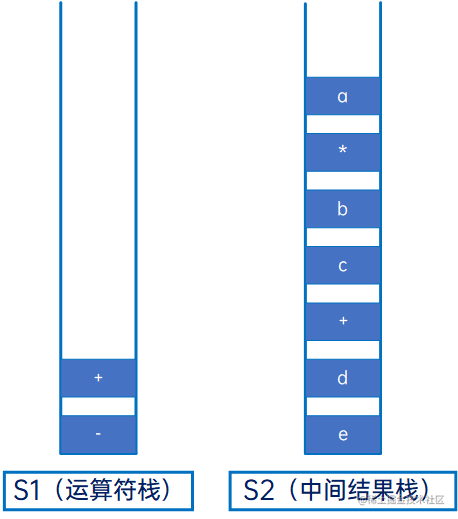
中缀表达式的所有字符都已读取完,这时,将S1的所有元素依次弹出,压入S2:
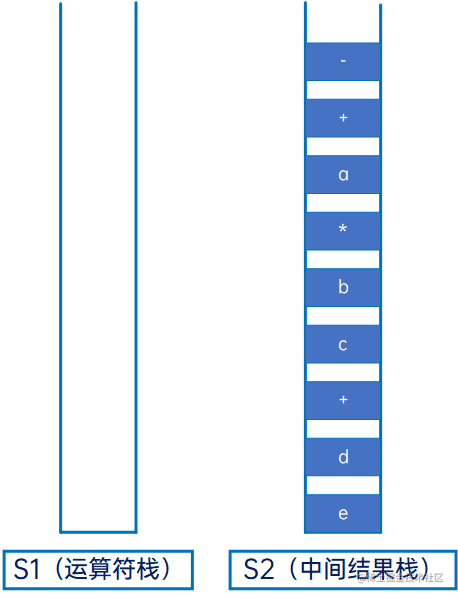
再将S2依次读出,得到前缀表达式结果:
- + a * b c + d e
我们用两栈共享空间的方式来实现代码:
/*** 判断字符串是否是数字** @param val 待判断的字符串* @return 是数字则返回true,否则返回false* @author Korbin* @date 2023-01-16 16:53:26**/
private boolean isData(String val) {Pattern p = Pattern.compile("^[a-zA-Z0-9]+$");return p.matcher(val).find();
}/*** 中缀表达式转前缀表达式** @param infix 中缀表达式* @return 前缀表达式* @author Korbin* @date 2023-01-16 11:49:29**/
public String infix2Prefix(String[] infix) {// 定义一个双向栈// 左边栈为S1,为运算符栈// 右边栈为S2,为中间结果栈BidirectionalStack<String> stack = new BidirectionalStack<>();stack.init(infix.length);for (int i = infix.length - 1; i >= 0; i--) {// 从右至左迭代中缀表达式String curStr = infix[i];// 取出运行符栈的栈顶元素String topOperator = null;try {topOperator = stack.getTop(1);} catch (Exception e) {// do nothing}// 如果为操作数直接入中间结果栈if (isData(curStr)) {// 操作数stack.push(curStr, 2);} else if (curStr.equals("(")) {// 左括号while (null != topOperator && !topOperator.equals(")")) {// 弹出运算符栈的元素,并压入中间结果栈,直到遇到右括号为止stack.push(stack.pop(1), 2);try {topOperator = stack.getTop(1);} catch (Exception e) {// do nothingtopOperator = null;}}if (null != topOperator) {// 抛弃右括号stack.pop(1);}} else if (curStr.equals(")")) {// 右括号// 直接进入运算符栈stack.push(curStr, 1);} else if (curStr.equals("+") || curStr.equals("-") || curStr.equals("*") || curStr.equals("/")) {// 运算符boolean inserted = false;while (!inserted) {if (null == topOperator || topOperator.equals(")")) {// 运算符栈顶为空或栈顶元素为右括号// 直接入栈到运算符栈,并结束stack.push(curStr, 1);inserted = true;} else if (curStr.equals("*") || curStr.equals("/") || topOperator.equals("+") ||topOperator.equals("-")) {// 优先级比栈顶运算符的较高或相等// 即:待比较的字符为乘或除,或者运算符栈顶元素为加或减时// 直接入栈到运算符栈,并结束stack.push(curStr, 1);inserted = true;} else {// 弹出运算符栈的元素,并压入中间结果栈,然后继续比较运算符栈的栈顶元素stack.push(stack.pop(1), 2);try {topOperator = stack.getTop(1);} catch (Exception e) {// do nothingtopOperator = null;}}}} else {// 其他情况,例如为空时,1直接入中间结果栈if (!curStr.equals(" ")) {stack.push(curStr, 2);}}}// 然后将运算符栈中的所有元素再压入中间结果栈while (!stack.isEmpty(1)) {stack.push(stack.pop(1), 2);}// 得到结果StringBuilder result = new StringBuilder();while (!stack.isEmpty(2)) {result.append(stack.pop(2));}return result.toString();}
6.3 中缀表达式转后缀表达式的代码实现
(1) 初始化两个栈:运算符栈S1和储存中间结果的栈S2;
(2) 从左至右扫描中缀表达式;
(3) 遇到操作数时,将其压入S2;
(4) 遇到运算符时,比较其与S1栈顶运算符的优先级:
1) 如果S1为空,或栈顶运算符为左括号“(”,则直接将此运算符入栈;
2) 否则,若优先级比栈顶运算符的高,也将运算符压入S1(注意转换为前缀表达式时是优先级较高或相同,而这里则不包括相同的情况);
3) 否则,将S1栈顶的运算符弹出并压入到S2中,然后取出S1中新的栈顶元素,再次转到(4)进行比较;
(5) 遇到括号时:
1) 如果是左括号“(”,则直接压入S1;
2) 如果是右括号“)”,则依次弹出S1栈顶的运算符,并压入S2,直到遇到左括号为止,此时将这一对括号丢弃;
(6) 重复步骤(2)至(5),直到表达式的最右边;
(7) 将S1中剩余的运算符依次弹出并压入S2;
(8) 依次弹出S2中的元素并输出,结果的逆序即为中缀表达式对应的后缀表达式(转换为前缀表达式时不用逆序)。
&msp; 然后以以下表达式为例:
a + b * c - (d + e)
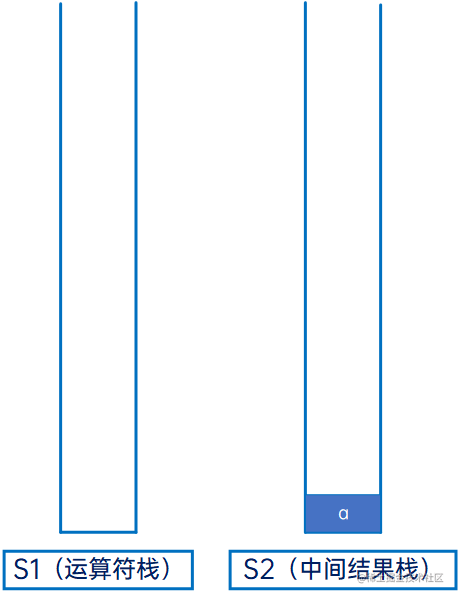
先定义两个空的栈:

然后从头开始迭代,先是“a”,操作数,直接压入S2:
然后是“+”,运算符,与S1的栈顶元素比较,因S1的栈顶元素为空,因此直接压入S1:
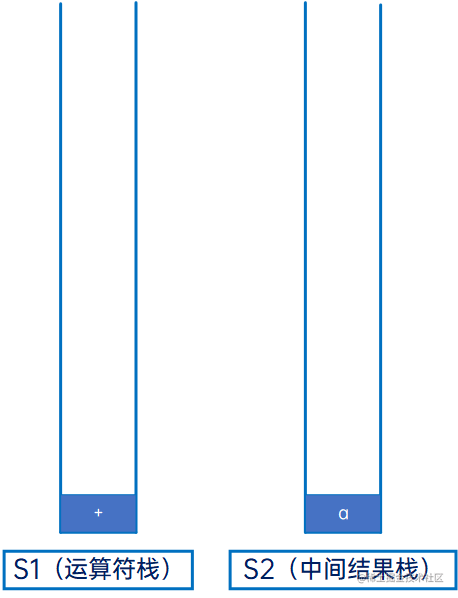
然后是“b”,操作数,直接压入S2:

然后是“*”,运算符,与S1的栈顶元素“+”比较,优先级较高,直接压入S1:
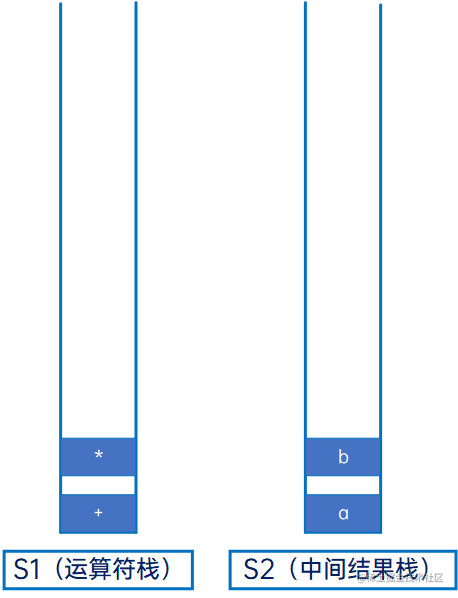
然后是“c”,操作数,直接压入S2:
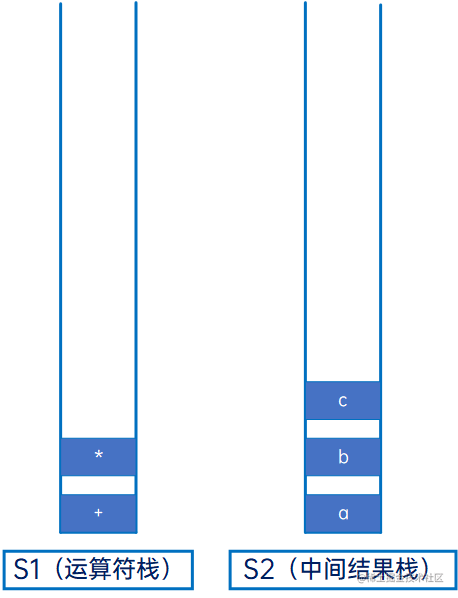
然后是“-”,操作数,与S1的栈顶元素“”比较,发现优先级低,因此将“”从S1弹出,压入S2:
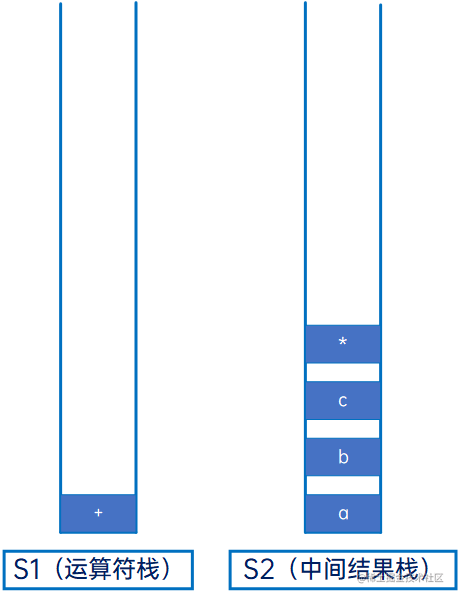
继续与S1新的栈顶元素“+”比较,优先级相同,将“+”从S1弹出,压入S2:
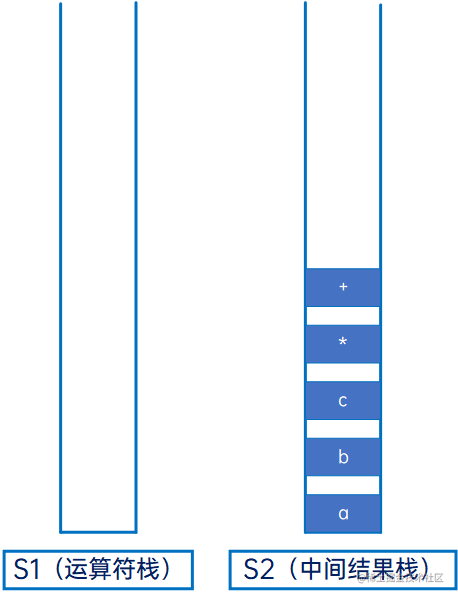
继续与S1新的栈顶元素比较,发现S1为空,因此直接将“-”压入S1:
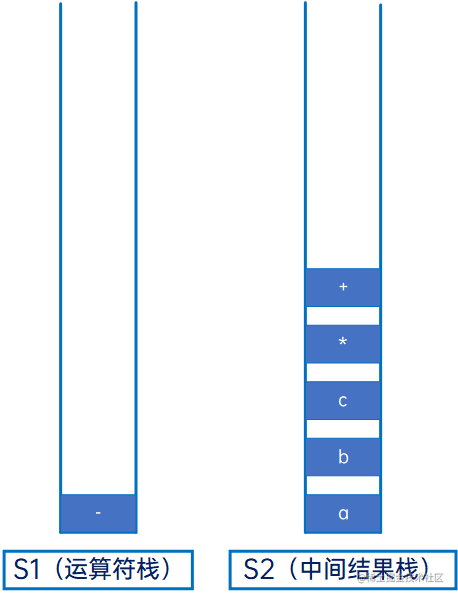
然后是“(”,直接压入S1:
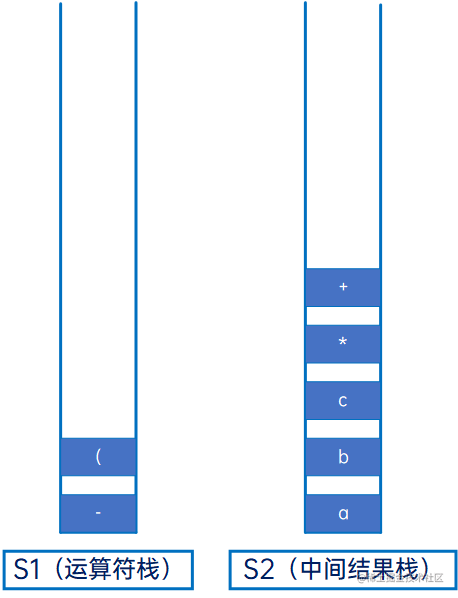
然后是“d”,操作数,直接压入S2:
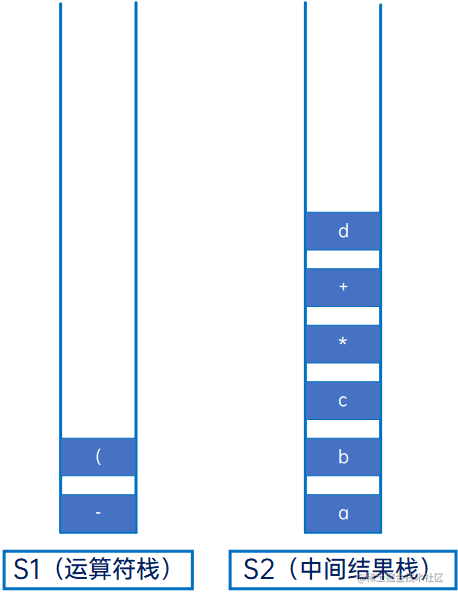
然后是“+”,运算符,与S1的栈顶元素“(”比较,因此是左括号,因此直接压入S1:
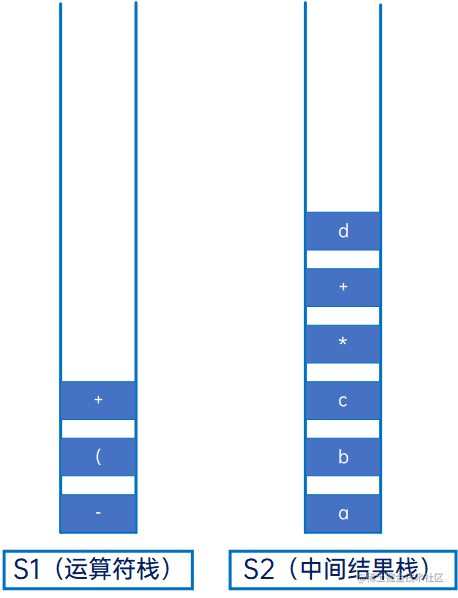
然后是“e”,操作数,直接压入S2:

然后是“)”,依次弹出S1的元素,压入S2,直到遇到左括号,然后把这一对括号去掉:
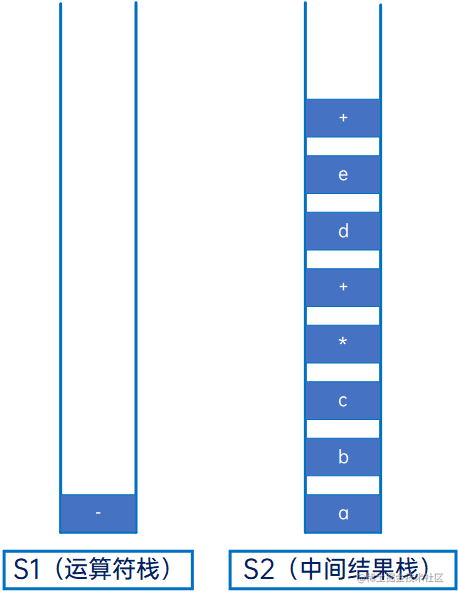
迭代完毕,把S1剩余的元素依次压入S2:

从S2中依次读取出结果:
- + e d + * c b a
reverse,得到后缀表达式结果:
a b c * + d e + -
代码如下所示:
/*** 中缀表达式转后缀表达式** @param infix 后缀表达式* @return 前缀表达式* @author Korbin* @date 2023-01-16 11:49:29**/
public String infix2Suffix(String[] infix) {// 定义一个双向栈// 左边栈为S1,为运算符栈// 右边栈为S2,为中间结果栈BidirectionalStack<String> stack = new BidirectionalStack<>();stack.init(infix.length);for (int i = 0; i <= infix.length - 1; i++) {// 从左至右迭代中缀表达式String curStr = infix[i];// 取出运行符栈的栈顶元素String topOperator = null;try {topOperator = stack.getTop(1);} catch (Exception e) {// do nothing}// 如果为操作数直接入中间结果栈if (isData(curStr)) {// 操作数stack.push(curStr, 2);} else if (curStr.equals("(")) {// 左括号// 直接进入运算符栈stack.push(curStr, 1);} else if (curStr.equals(")")) {// 右括号while (null != topOperator && !topOperator.equals("(")) {// 弹出运算符栈的元素,并压入中间结果栈,直到遇到左括号为止stack.push(stack.pop(1), 2);try {topOperator = stack.getTop(1);} catch (Exception e) {// do nothingtopOperator = null;}}if (null != topOperator) {// 抛弃右括号stack.pop(1);}} else if (curStr.equals("+") || curStr.equals("-") || curStr.equals("*") || curStr.equals("/")) {// 运算符boolean inserted = false;while (!inserted) {if (null == topOperator || topOperator.equals("(")) {// 运算符栈顶为空或栈顶元素为左括号// 直接入栈到运算符栈,并结束stack.push(curStr, 1);inserted = true;} else if ((curStr.equals("*") || curStr.equals("/")) &&(topOperator.equals("+") || topOperator.equals("-"))) {// 优先级比栈顶运算符的较高// 即:运算符栈顶元素为加或减时// 直接入栈到运算符栈,并结束stack.push(curStr, 1);inserted = true;} else {// 弹出运算符栈的元素,并压入中间结果栈,然后继续比较运算符栈的栈顶元素stack.push(stack.pop(1), 2);try {topOperator = stack.getTop(1);} catch (Exception e) {// do nothingtopOperator = null;}}}} else {// 其他情况,例如为空时,1直接入中间结果栈if (!curStr.equals(" ")) {stack.push(curStr, 2);}}}// 然后将运算符栈中的所有元素再压入中间结果栈while (!stack.isEmpty(1)) {stack.push(stack.pop(1), 2);}// 得到结果StringBuilder result = new StringBuilder();while (!stack.isEmpty(2)) {result.append(stack.pop(2));}return result.reverse().toString();
}
6.4 使用前缀表达式计算四则运算
现有四则运算表达式:
9 + (3 - 1) * 3 + 10 / 2
转化成前缀表达式后是:
+ + 9 * - 3 1 3 / 10 2
先初始化一个空栈,然后从右向左开始处理,规则是:如果是数字,则进栈,如果是符号,就将处于栈顶的两个数字出栈,进行运算,运算结果进栈,一直到最终获得结果,注意,栈顶元素是“x”,栈的第二个元素是“y”,则当是运算符“zz”时,运算方式应是“x zz y”。
如上述前缀表达式,先是“2”,直接进栈:

然后是“10”,直接进栈:

然后是“/”,取出栈顶的两个元素,然后进行“10 / 2”处理,得到5,然后入栈:

然后是“3”,直接进栈:

然后是“1”,直接进栈:

然后是“3”,直接进栈:
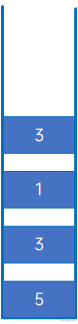
然后是“-”,取出栈顶的两个元素,进行“3 - 1”处理,得到2,然后入栈:

然后是“*”,取出栈顶的两个元素,进行“2 * 3”处理,得到6,然后入栈:

然后是“9”,直接进栈:

然后是“+”,取出栈顶的两个元素,进行“9 + 6”处理,得到15,然后入栈:

然后是“+”,取出栈顶的两个元素,进行“15 + 5”处理,得到20,然后入栈:

于是得到最终结果20。
代码如下所示:
/*** 使用前缀表达式计算** @param prefixExpression 前缀表达式* @return 计算结果* @author Korbin* @date 2023-01-16 18:17:01**/
public double prefixCalc(String[] prefixExpression) {LinkStack<String> stack = new LinkStack<>();int length = prefixExpression.length;for (int i = length - 1; i >= 0; i--) {String curStr = prefixExpression[i];if (isData(curStr)) {// 如果是操作数,则直接入栈stack.push(curStr);} else {// 否则,使用第二个元素 运算符 栈顶元素得出结果后,再将结果入栈double firstData = Double.parseDouble(stack.pop().getData());double secondData = Double.parseDouble(stack.pop().getData());double value = 0;switch (curStr) {case "+":value = firstData + secondData;break;case "-":value = firstData - secondData;break;case "*":value = firstData * secondData;break;case "/":value = firstData / secondData;break;}stack.push(String.valueOf(value));}}return Double.parseDouble(stack.pop().getData());
}
6.5 使用后缀表达式计算四则运算
现有四则运算表达式:
9 + (3 - 1) * 3 + 10 / 2
转化成后缀表达式后是:
9 3 1 - 3 * + 10 2 / +
先初始化一个空栈,然后从左向右开始处理,规则是:如果是数字,则进栈,如果是符号,就将处于栈顶的两个数字出栈,进行运算,运算结果进栈,一直到最终获得结果,注意,栈顶元素是“x”,栈的第二个元素是“y”,则当是运算符“zz”时,运算方式应是“y zz x”。
如上述后缀表达式,先是“9”,直接进栈:

然后是“3”,直接进栈:

然后是“1”,直接进栈:

然后是“-”,取出栈顶的两个值,进行“3 - 1”处理,得到2,再进栈:

然后是“3”,直接进栈:

然后是“*”,取出栈顶的两个值,进行“2 * 3”处理,得到6,再进栈:

然后是“+”,取出栈顶的两个值,进行“9 + 6”处理,得到15,再进栈:

然后是“10”,直接进栈:

然后是“2”,直接进栈:

然后是“/”,取出栈顶的两个值,进行“10 / 2”处理,得到5,再进栈:

然后是“+”,取出栈顶的两个值,进行“15 + 5”处理,得到20,再进栈:

这样就得到了最终结果。
代码如下所示:
/*** 使用后缀表达式计算** @param suffixExpression 后缀表达式* @return 计算结果* @author Korbin* @date 2023-01-16 18:17:01**/
public double suffixCalc(String[] suffixExpression) {LinkStack<String> stack = new LinkStack<>();int length = suffixExpression.length;for (int i = 0; i <= length - 1; i++) {String curStr = suffixExpression[i];if (isData(curStr)) {// 如果是操作数,则直接入栈stack.push(curStr);} else {// 否则,使用栈顶元素 运算符 第二个元素得出结果后,再将结果入栈double secondData = Double.parseDouble(stack.pop().getData());double firstData = Double.parseDouble(stack.pop().getData());double value = 0;switch (curStr) {case "+":value = firstData + secondData;break;case "-":value = firstData - secondData;break;case "*":value = firstData * secondData;break;case "/":value = firstData / secondData;break;}stack.push(String.valueOf(value));}}return Double.parseDouble(stack.pop().getData());
}
6.6 总结
可见,无论在中缀转前缀或中缀转后缀时,或者在使用前缀或后缀进行计算时,都可以使用栈来进行辅助计算。
注:本文为程 杰老师《大话数据结构》的读书笔记,其中一些示例和代码是笔者阅读后自行编制的。
相关文章:

大话数据结构-栈
1 概述 栈(Stack)是限定仅在表尾进行插入和删除操作的线性表。 允许插入和删除的一端称为栈顶(top),另一端称为栈底(bottom),不含任何数据元素的栈称为空栈,栈又称为后进…...

javaFx实现放大镜效果——圆形、矩形、三角形放大镜,拖动调整放大镜大小,设置放大倍数
系列文章专栏:javafx图形绘制、桌面录屏录音源码合集 目录 一、实现的效果 二、实现思路 三、程序实现...

什么是客户忠诚度?建立忠诚文化的 5 种方法
客户忠诚度影响企业的各个方面,例如收入、品牌形象、预算分配和产品路线图。拥有忠实的客户群对于建立成功的企业至关重要,因为您的客户是您的主要拥护者,有助于为您的企业营造积极的氛围。 什么是客户忠诚度? 客户忠诚度衡量客户…...
【ROS2知识】关于colcon编译和ament指定
一、说明 这里说说编译和包生成的操作要点,以python包为例。对于初学者来说,colcon和ament需要概念上搞清楚,与此同时,工作空间、包、节点在一个工程中需要熟练掌握。本文以humble版的ROS2,进行python编程的实现。 二、…...

数据结构: 最小栈
最小栈的特色是保持栈后进先出的特性,同时能够以O(1)复杂度获得当前栈的最小值。 栈是比较好实现的,直接搞个链表,从头部删除和添加即可。 最小栈的核心逻辑是: 因为栈是后进先出的,因此栈顶元素之下的数字永远在栈…...
STM32之PWM
PWMPWM,英文名Pulse Width Modulation,是脉冲宽度调制缩写,它是通过对一系列脉冲的宽度进行调制,等效出所需要的波形(包含形状以及幅值),对模拟信号电平进行数字编码,也就是说通过调…...

操作系统(1.1)--引论
目录 一、操作系统的目标和作用 1.操作系统的目标 2.操作系统的作用 2.1 OS作为用户与计算机硬件系统之间的接口 2.2 OS作为计算机系统资源的管理者 2.3 0S实现了对计算机资源的抽象 3. 推动操作系统发展的主要动力 二、操作系统的发展过程 1.无操作系统的计算机系统…...
Spring boot + mybatis-plus 遇到 数据库字段 创建不规范 大驼峰 下划线 导致前端传参数 后端收不到参数 解决方案
最近使用springboot 连接了一个 sqlserver 数据库 由于数据库年数久远 ,建表字段不规范 大驼峰 下划线的字段名都有 但是 java 中 Spring boot mybatis-plus 又严格按照小驼峰 格式 生成实体类 如果不是小驼峰格式 Data 注解 get set 方法 在前端请求参数 使用这个…...

JavaScript String 字符串对象
文章目录JavaScript String 字符串对象JavaScript 字符串字符串(String)在字符串中查找字符串内容匹配替换内容字符串大小写转换字符串转为数组特殊字符字符串属性和方法JavaScript String 字符串对象 String 对象用于处理已有的字符块。 JavaScript 字…...

Lazada如何做好店铺运营?产品定价是关键
1.东南亚各国状况一览(对比中国) 2.东南亚消费水平真的很低? 精准定价的意义:定价过高,失去核心竞争力;定价过低,亏本对市场失去信心;价格改动,流量下降 定价公式&#…...

空口协议Eapol、802.11 Action、802.11 BAR 和 802.11BA、802.11 Encrypted Data讲解
如下报文 可以看到,除了有之前开放认证的报文之外,还多了 EAPOL 次握手的报文。另外,还有其他几种类型的报文:802.11 Action、802.11 BAR 和 802.11BA、802.11 Encrypted Data 密匙认证协议EAPOL: EAP是Extensible Authentication Protocol的缩写,EAPOL就是(EAP…...

C++类和对象
目录 一、C类定义 二、定义C对象 三、访问数据成员 四、类和对象详解 C 在 C 语言的基础上增加了面向对象编程,C 支持面向对象程序设计。类是 C 的核心特性,通常被称为用户定义的类型。 类用于指定对象的形式,它包含了数据表示法和用于处…...

Leetcode.面试题 05.02 二进制数转字符串
题目链接 面试题 05.02 二进制数转字符串 Mid 题目描述 二进制数转字符串。给定一个介于0和1之间的实数(如0.72),类型为double,打印它的二进制表达式。如果该数字无法精确地用32位以内的二进制表示,则打印“ERROR”。…...

UDPTCP网络编程
udp编程接口 一个UDP程序的编写可以分为3步: 创建一个网络套接字: 它相当于文件操作时的文件描述符,是一个程序进行网络通讯的门户, 所有的网络操作都要基于它 绑定IP和端口: 需要为网络套接字填充IP和端口信息 但是…...

【微信小程序】-- 全局配置 -- tabBar(十七)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &…...

Cortex-A7中断控制器GIC
Cortex-A7中断控制器GIC 中断号 芯片内部的中断都会引起IRQ InterruptGIC将所有的中断源(最多1020个中断ID)分为三类: SPI(SharedPeripheralInterrupt)共享中断,外部中断都属于SPI中断 [ID32-1019]PPI(PrivatePeripheralInterrupt)私有中断 [ID16-31]SGI(Software-…...
JavaSE:常用类
前言从现在开始进入高级部分的学习,鼓励自己一下!画个大饼: 常用类->集合框架->IO流->多线程->网络编程 ->注解与反射->GUI很重要的东西,不能不会!Object类祖宗类,主要方法:t…...
Element中树形控件在项目中的实际应用
文章目录1、使用目的2、官网组件3、组合使用组件案例4、在项目中实际应用4.1 组合组件的使用4.1.2 代码落地4.1.3 后台接口数据4.1.4 实际效果官网连接直达:Tree树形控件的使用 1、使用目的 用清晰的层级结构展示信息,可展开或折叠。 2、官网组件 <…...
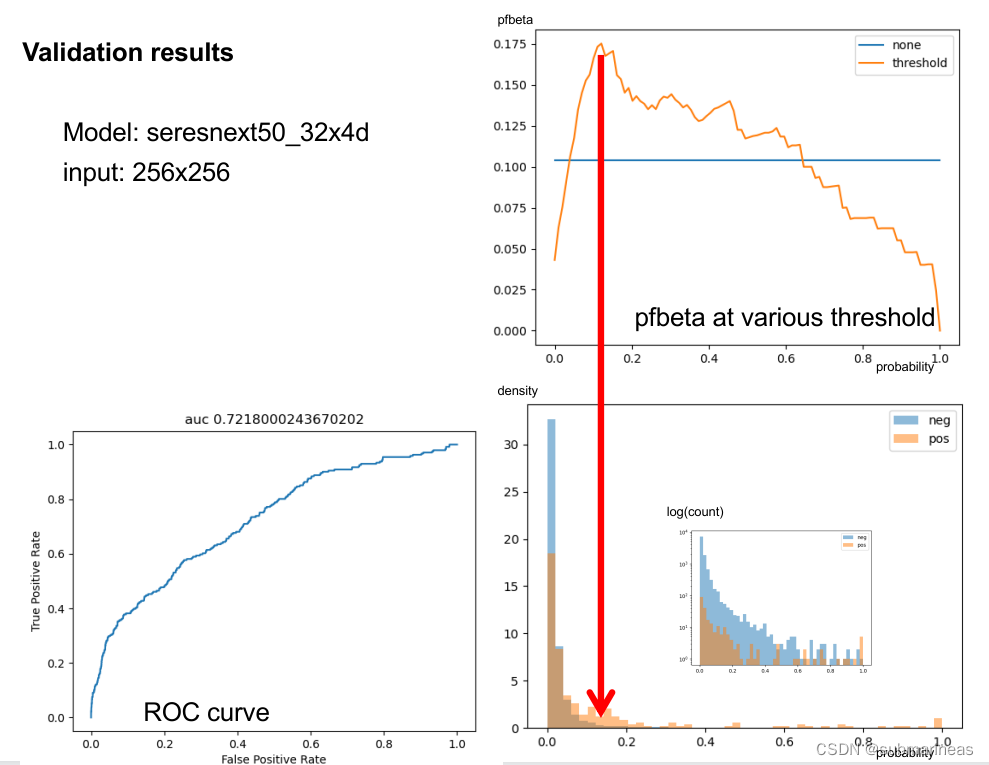
kaggle RSNA 比赛过程总结
引言 算算时间,有差不多两年多没在打kaggle了,自20年最后一场后(其实之前也就打过两场,一场打铁,一场表格赛是金是银不太记得,当时相当于刺激战场,过拟合lb大赛太刺激了,各种trick只…...

51单片机入门————LED灯的控制
LED的电路图通过原理图看出,LED灯是接单片机芯片的P20~P27的一共有8个LED,51单片机也是8字节的P20x010xFE————1111 1110P20xFE可以表示把在P2端的第一个灯点亮1 表示高电平0表示低电平当为0的时候形成一个完整回路,电流从高电平流向低电平…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

TCP/IP 网络编程 | 服务端 客户端的封装
设计模式 文章目录 设计模式一、socket.h 接口(interface)二、socket.cpp 实现(implementation)三、server.cpp 使用封装(main 函数)四、client.cpp 使用封装(main 函数)五、退出方法…...

UE5 音效系统
一.音效管理 音乐一般都是WAV,创建一个背景音乐类SoudClass,一个音效类SoundClass。所有的音乐都分为这两个类。再创建一个总音乐类,将上述两个作为它的子类。 接着我们创建一个音乐混合类SoundMix,将上述三个类翻入其中,通过它管理每个音乐…...
