动态规划(背包问题)
动态规划
文章目录
- 动态规划
- 一、背包问题
- 一、01背包
- 二、完全背包问题
- 三、多重背包问题
- 四、分组背包问题
一、背包问题
一、01背包
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
(1)F[i,j]:只在前i个物品里选,且总体积不超过j的最大价值(2)不选第i个:F[i−1][j](3)选第i个:F[i−1][j−v[i]]+w[i](4)F[i][j]=max(F[i−1][j],F[i−1][j−v[i]]+w[i])\begin{align} &(1)F[i,j]:只在前i个物品里选,且总体积不超过j的最大价值\\ &(2)不选第i个:F[i-1][j]\\ &(3)选第i个 :F[i-1][j-v[i]]+w[i]\\ &(4)F[i][j]=max(F[i-1][j],F[i-1][j-v[i]]+w[i]) \end{align} (1)F[i,j]:只在前i个物品里选,且总体积不超过j的最大价值(2)不选第i个:F[i−1][j](3)选第i个:F[i−1][j−v[i]]+w[i](4)F[i][j]=max(F[i−1][j],F[i−1][j−v[i]]+w[i])
优化前:
memset(f,0,sizeof f);for(int i=1;i<=n;i++)for(int j=0;j<=m;j++){f[i][j]=f[i-1][j]; //不选if(j>=v[i]) f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]); //选}cout<<f[n][m]<<endl;
优化后:(每次只会用到上一层的状态)
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1010;
int n,m;
int f[N];
int v[N],w[N];
int main()
{cin>>n>>m;for(int i=1;i<=n;i++)cin>>v[i]>>w[i];memset(f,0,sizeof f);for(int i=1;i<=n;i++)for(int j=m;j>=v[i];j--){f[j]=max(f[j],f[j-v[i]]+w[i]); //选}cout<<f[m]<<endl;return 0;}
二、完全背包问题
有 N 种物品和一个容量是 V 的背包,每种物品都有无限件可用。
第 i种物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
(1)F[i,j]:只在前i个物品里选,且总体积不超过j的最大价值(2)选k(k>=0)个物品i:F[i−1][j−k∗v[i]]+K∗w[i]\begin{align} &(1)F[i,j]:只在前i个物品里选,且总体积不超过j的最大价值\\ &(2)选k(k>=0)个物品i:F[i-1][j-k*v[i]]+K*w[i]\\ \end{align} (1)F[i,j]:只在前i个物品里选,且总体积不超过j的最大价值(2)选k(k>=0)个物品i:F[i−1][j−k∗v[i]]+K∗w[i]
优化前:
for(int i = 1 ; i<=n ;i++)for(int j = 0 ; j<=m ;j++){for(int k = 0 ; k*v[i]<=j ; k++)f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);}
优化:
f[i , j ] = max( f[i-1,j] , f[i-1,j-v]+w , f[i-1,j-2*v]+2*w , f[i-1,j-3*v]+3*w , .....)
f[i , j-v]= max( f[i-1,j-v] , f[i-1,j-2*v] + w , f[i-1,j-3*v]+2*w , .....)
由上两式,可得出如下递推关系: f[i][j]=max(f[i,j-v]+w , f[i-1][j])
for(int i = 1 ; i <= n ; i++)
for(int j = 0 ; j <= m ; j ++)
{f[i][j] = f[i-1][j];if(j-v[i]>=0)f[i][j] = max(f[i][j],f[i-1][j-v[i]]+w[i]);
}
优化变一维:
for(int i = 1 ; i<=n ;i++)for(int j = v[i] ; j<=m ;j++)//注意了,这里的j是从小到大枚举,和01背包不一样{f[j] = max(f[j],f[j-v[i]]+w[i]);}
三、多重背包问题
有 N 种物品和一个容量是 V 的背包。
第 i 种物品最多有 si 件,每件体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
思路1:参考完全背包
int n,m;
int v[N],w[N],s[N];
int f[N][N];int main()
{cin>>n>>m;for(int i=1;i<=n;i++) cin>>v[i]>>w[i]>>s[i];for(int i=1;i<=n;i++)for(int j=0;j<=m;j++)for(int k=0;k<=s[i]&&k*v[i]<=j;k++)f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);cout<<f[n][m]<<endl;return 0;
}
思路2**:二进制优化将n种物品,每种Si个的多重背包,拆分打包看成N件物品(组)的01背包问题**
(1)例如当s[i]=7时(2)将其拆分为:1,2,4的三组,就可以凑出0−7中的任意数(3)s[i]=9时:1,2,4,2就可以凑出0−7中的任意数\begin{align} &(1)例如当s[i]=7时\\ &(2)将其拆分为:1,2,4的三组,就可以凑出0-7中的任意数\\ &(3)s[i]=9时:1,2,4,2就可以凑出0-7中的任意数 \end{align} (1)例如当s[i]=7时(2)将其拆分为:1,2,4的三组,就可以凑出0−7中的任意数(3)s[i]=9时:1,2,4,2就可以凑出0−7中的任意数
#include<iostream>using namespace std;const int M=12000;int n,m;
int f[M],v[M],w[M];
int main()
{cin>>n>>m;int cnt=0;while(n--){int a,b,c;cin>>a>>b>>c;int t=1;while(c>=t){v[++cnt]=a*t;w[ cnt]=b*t;c-=t;t=t*2;}if(c) {v[++cnt]=a*c; w[cnt]=b*c;}}n=cnt;//转化为了01背包for(int i=1;i<=n;i++)for(int j=m;j>=v[i];j--)f[j]=max(f[j],f[j-v[i]]+w[i]);cout<<f[m]<<endl;return 0;
}
四、分组背包问题
有 N 组物品和一个容量是 V 的背包。
每组物品有若干个,同一组内的物品最多只能选一个。
每件物品的体积是 vij,价值是 wij,其中 i 是组号,j是组内编号。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
(1)F[i,j]:只在前i组里选,且总体积不超过j的最大价值(2)不选:F[i−1][j](3)选i组的第k个:F[i−1][j−v[i][k]]+w[i][k]\begin{align} &(1)F[i,j]:只在前i组里选,且总体积不超过j的最大价值\\ &(2)不选:F[i-1][j]\\ &(3)选i组的第k个:F[i-1][j-v[i][k]]+w[i][k] \end{align} (1)F[i,j]:只在前i组里选,且总体积不超过j的最大价值(2)不选:F[i−1][j](3)选i组的第k个:F[i−1][j−v[i][k]]+w[i][k]
#include<iostream>
using namespace std;
const int N=110;
int n,m;
int s[N],v[N][N],w[N][N];
int f[N][N];
int main()
{cin>>n>>m;for(int i=1;i<=n;i++){cin>>s[i];for(int j=0;j<s[i];j++)cin>>v[i][j]>>w[i][j];}for(int i=1;i<=n;i++)for(int j=0;j<=m;j++){f[i][j]=f[i-1][j]; //不选for(int k=0;k<s[i];k++){if(j>=v[i][k]) f[i][j]=max(f[i][j],f[i-1][j-v[i][k]]+w[i][k]); //选第k个}}cout<<f[n][m]<<endl;return 0;
}
相关文章:
)
动态规划(背包问题)
动态规划 文章目录动态规划一、背包问题一、01背包二、完全背包问题三、多重背包问题四、分组背包问题一、背包问题 一、01背包 有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。 第 i 件物品的体积是 vi,价值是 wi。 求解将哪些物品装入背包…...

04741自考计算机网络原理最详细汇总
04741自考计算机网络原理知识点总结 引言 第一章 计算机网络概述 1.计算机网络基本概念与网络结构 1.1 计算机网络的概念; 1.2 计算机网络结构 1.3 数据交换技术 1.4 计算机网络性能 1.5 计算机网络体系结构 1.6 计算机网络与因特网发展简史 第二章 网络应用 2.1 网络应用体系…...
 基本操作)
MySQL 入门学习笔记(二) 基本操作
MySQL 入门学习笔记(二) 数据库和表的基本操作 我们把一些表的集合称之为数据库,一个服务器中可以存在多个数据库.每个数据库中包含多个表,每个表都有一个名字作为标识,数据表则包含带有数据的记录. PS:SQL 语句对大小写不敏感. 操作数据库命令 在 MySQL 命令中,数据库用DAT…...
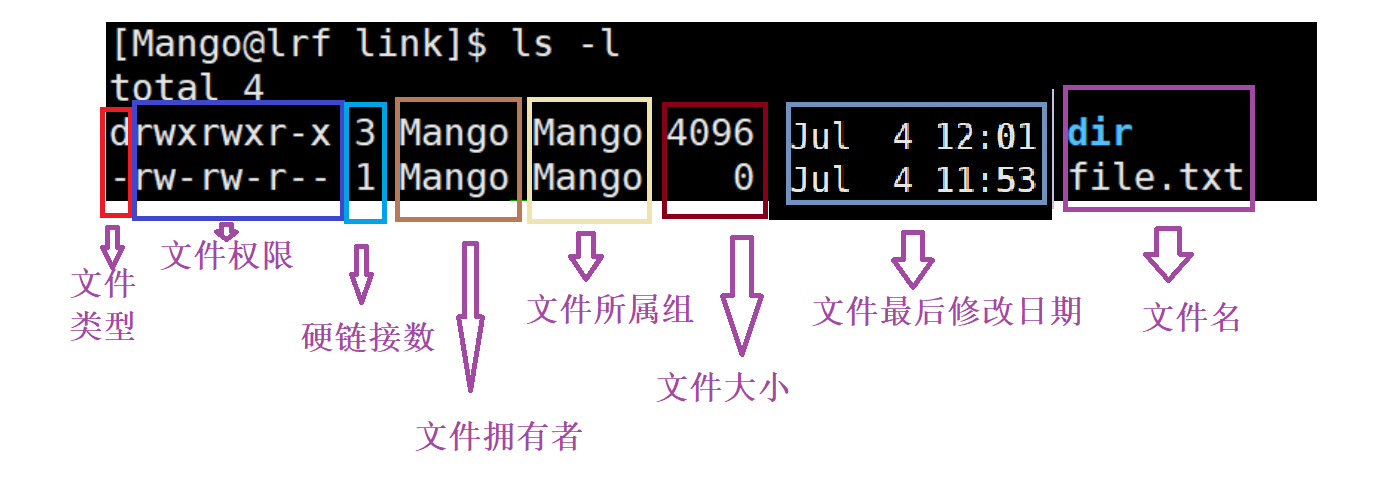
【Linux】理解文件系统
文章目录理解文件系统了解磁盘结构inode理解文件系统 了解磁盘结构 磁盘是计算机中的一个 机械设备 这个磁盘的盘片就像光盘一样,数据就在盘片上放着, 但是光盘是只读的,磁盘是可读可写的 机械硬盘的寻址的工作方式: 盘片不断旋转,磁头不断摆动,定位到特定的位置 我们可以把…...

Java如何String字符串带括号转成List
问题现象 今天在做一个需求:将存入数据库中的数据读到后解析成list遍历分析 数据格式: "[1677660600000, 1677660900000, 1677661200000]" "[5, 4, 4,3,2,0,0]" 我一开始想到的就是使用逗号分割即可 结果变成了这样的…...

react 使用 mqtt
也许很多人都好奇这个mqtt是什么东西,其实在互联网上可能不会使用到它,它是物联网上的东西,也是一种通信协议跟websocket。但它也能在浏览器跟服务器上跑,它的底层实现也是封装了websocket。 MQTT MQTT是一个客户端服务端架构的发…...

W25Q256被写保护如何修改
W25Q256被写保护如何修改1、 W25Q256数据读不到1.1 打印的寄存器的值1.2 可能原因1.3 解决办法1.4 用到的函数1、 W25Q256数据读不到 能够正确的读到ID,但是读到的数据不正确 1.1 打印的寄存器的值 0x2 BUSY :只读, 指令正在执行 WEL (1) &…...

论文投稿指南——中文核心期刊推荐(中国文学作品)
【前言】 🚀 想发论文怎么办?手把手教你论文如何投稿!那么,首先要搞懂投稿目标——论文期刊 🎄 在期刊论文的分布中,存在一种普遍现象:即对于某一特定的学科或专业来说,少数期刊所含…...

MySQL 问题总结
什么是MVCC? 说说MySQL实现MVCC的原理? MVCC,全称Multi-Version Concurrency Control,即多版本并发控制。MVCC是一种并发控制的方法,一般在数据库管理系统中,实现对数据库的并发访问。 对于「读已提交」和…...
62. 不同路径
62. 不同路径 一个机器人位于一个 m∗nm * nm∗n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。 问总共有多少条不同的路…...
在windows安装python3.11同时进行一个数据的练习
安装包百度网盘如下: 链接:https://pan.baidu.com/s/1l9H1GWP64LOxLaXXLie2uA?pwd6666 提取码:6666 1.我们选择自定义安装 2.当我们点了自定义安装后就直接next 3.修改路径,之后点击安装(install) 4.安装完成,进行…...

Java接口专题
基本介绍 接口给出一些没有实现的方法,封装到一起,到某个类使用时再根据具体情况把这些方法写出来。 注意:在jdk7之前,接口里所有的方法都是抽象方法。在jdk8之后接口中可以有静态方法,默认方法 interface 接口名{/…...

6招优化WordPress打开速度-让你的网站飞起来
为什么我们的WordPress网站比你的快? 我们的官网是使用WordPress框架搭建的,有没有发现我们的网站非常快,而你的WordPress网站比较慢呢?那是因为我们的网站经过了优化。 WordPress 很慢? 为什么很多人都会觉得 Word…...

春天到了,来一场 VoxEdit 创作大赛吧!
春天的气息扑面而来,这是让你尽情绽放创造力的最佳时机!我们将以「春天」为主题来一场 VoxEdit 大赛。在这里,你可以展示你的才华并赢得 $SAND 奖励! 无论你是专业的设计师,还是仅仅喜欢创造美丽的艺术,这场…...
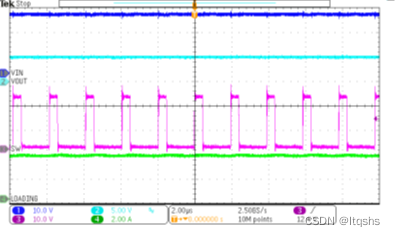
异步Buck和同步Buck的特点
1 介绍 随着时代的发展,工业,车载,通信,消费类等产品都提出了小型化,智能化的需求。相应的,对于这些系统中的电源模块提出了小型化的要求。目前,市场上依然存在很多异步Buck电源管理芯片使用的场…...
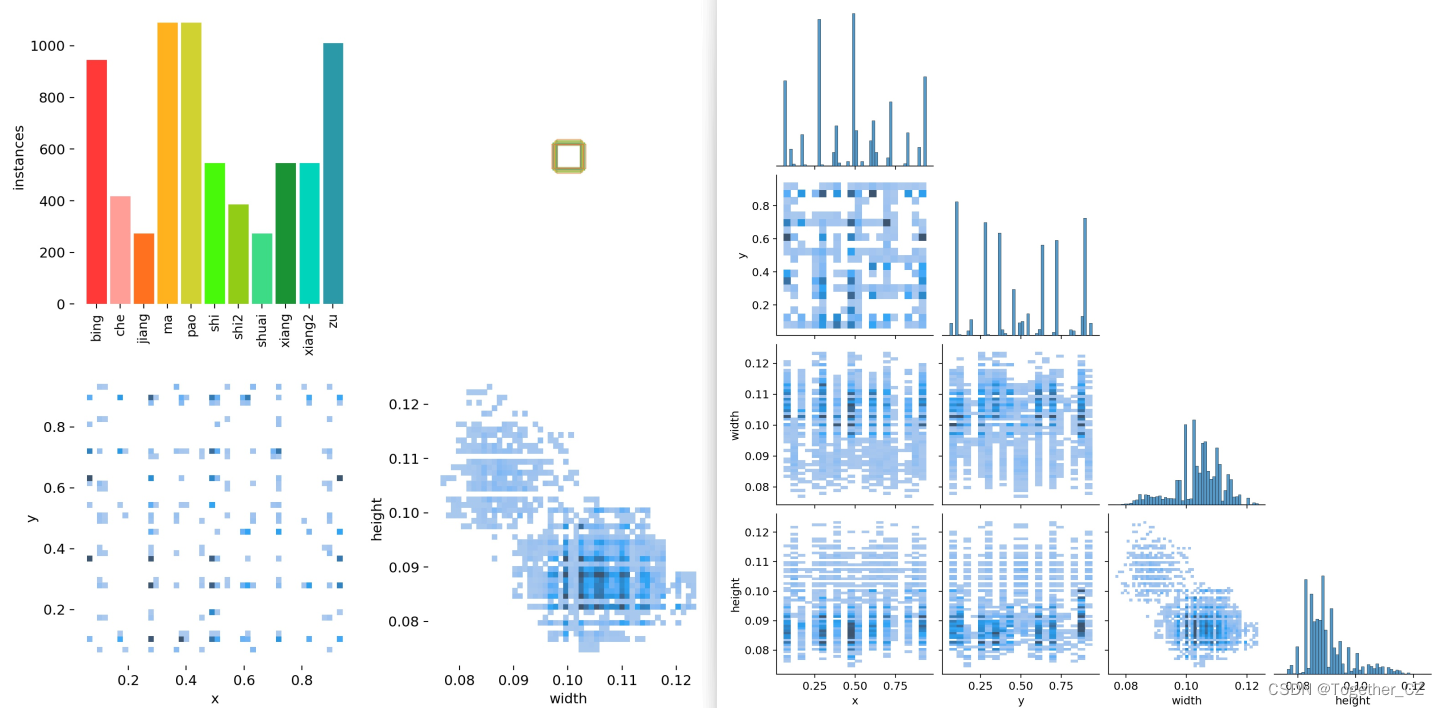
基于轻量级YOLO开发构建中国象棋目标检测识别分析系统
关于棋类相关的项目在我之前的博文里面都有做过,如下:《yolov5s融合SPD-Conv用于提升小目标和低分辨率图像检测性能实践五子棋检测识别》《YOLOV5融合SE注意力机制和SwinTransformer模块开发实践的中国象棋检测识别分析系统》《基于yolov5s实践国际象棋目…...

机器学习100天(三十五):035 贝叶斯公式
《机器学习100天》完整目录:目录 机器学习100天,今天讲的是:贝叶斯公式! 好了,上一节介绍完先验概率、后验概率、联合概率、全概率后,我们来看这样一个问题:如果我现在挑到了一个瓜蒂脱落的瓜,则该瓜是好瓜的概率多大? 显然,这是一个计算后验概率的问题,根据我们之…...

大话数据结构-栈
1 概述 栈(Stack)是限定仅在表尾进行插入和删除操作的线性表。 允许插入和删除的一端称为栈顶(top),另一端称为栈底(bottom),不含任何数据元素的栈称为空栈,栈又称为后进…...

javaFx实现放大镜效果——圆形、矩形、三角形放大镜,拖动调整放大镜大小,设置放大倍数
系列文章专栏:javafx图形绘制、桌面录屏录音源码合集 目录 一、实现的效果 二、实现思路 三、程序实现...

什么是客户忠诚度?建立忠诚文化的 5 种方法
客户忠诚度影响企业的各个方面,例如收入、品牌形象、预算分配和产品路线图。拥有忠实的客户群对于建立成功的企业至关重要,因为您的客户是您的主要拥护者,有助于为您的企业营造积极的氛围。 什么是客户忠诚度? 客户忠诚度衡量客户…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...

鸿蒙HarmonyOS 5军旗小游戏实现指南
1. 项目概述 本军旗小游戏基于鸿蒙HarmonyOS 5开发,采用DevEco Studio实现,包含完整的游戏逻辑和UI界面。 2. 项目结构 /src/main/java/com/example/militarychess/├── MainAbilitySlice.java // 主界面├── GameView.java // 游戏核…...
