当前位置： 首页 > news >正文

maven打包插件maven-jar-plugin与spring-boot-maven-plugin

news 2026/2/8 16:09:49

maven几种打包插件介绍

文章目录

    • 🔊1.spring-boot-maven-plugin
      • 打包后效果
    • 📕2.maven-jar-plugin
    • 打包后效果
    • 🖊️最后总结

🔊1.spring-boot-maven-plugin

<plugins><plugin><groupId>org.springframework.boot</groupId><artifactId>spring-boot-maven-plugin</artifactId></plugin>
</plugins>

spring-boot-maven-plugin：springboot项目默认的打包工具，默认情况下只会将项目源码编译生成的class文件和资源文件依赖jar包都打进来，即打包自己项目的class文件+环境变量+静态资源文件+依赖jar（不会把依赖jar反编译为class文件打入）。

使用2.2.1.RELEASE版本需要maven版本在2.0及以上，JDK在1.8及以上。

打包后效果

image-20231215101626240

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

📕2.maven-jar-plugin

<plugins><plugin><groupId>org.apache.maven.plugins</groupId><artifactId>maven-jar-plugin</artifactId><configuration><excludes><exclude>com/woniu/TestApplication.class</exclude></excludes></configuration></plugin>
</plugins>

插件：使用maven-jar-plugi插件

默认的打包方式，用来打普通的project JAR包，不会将依赖的jar打包进去

打包后效果

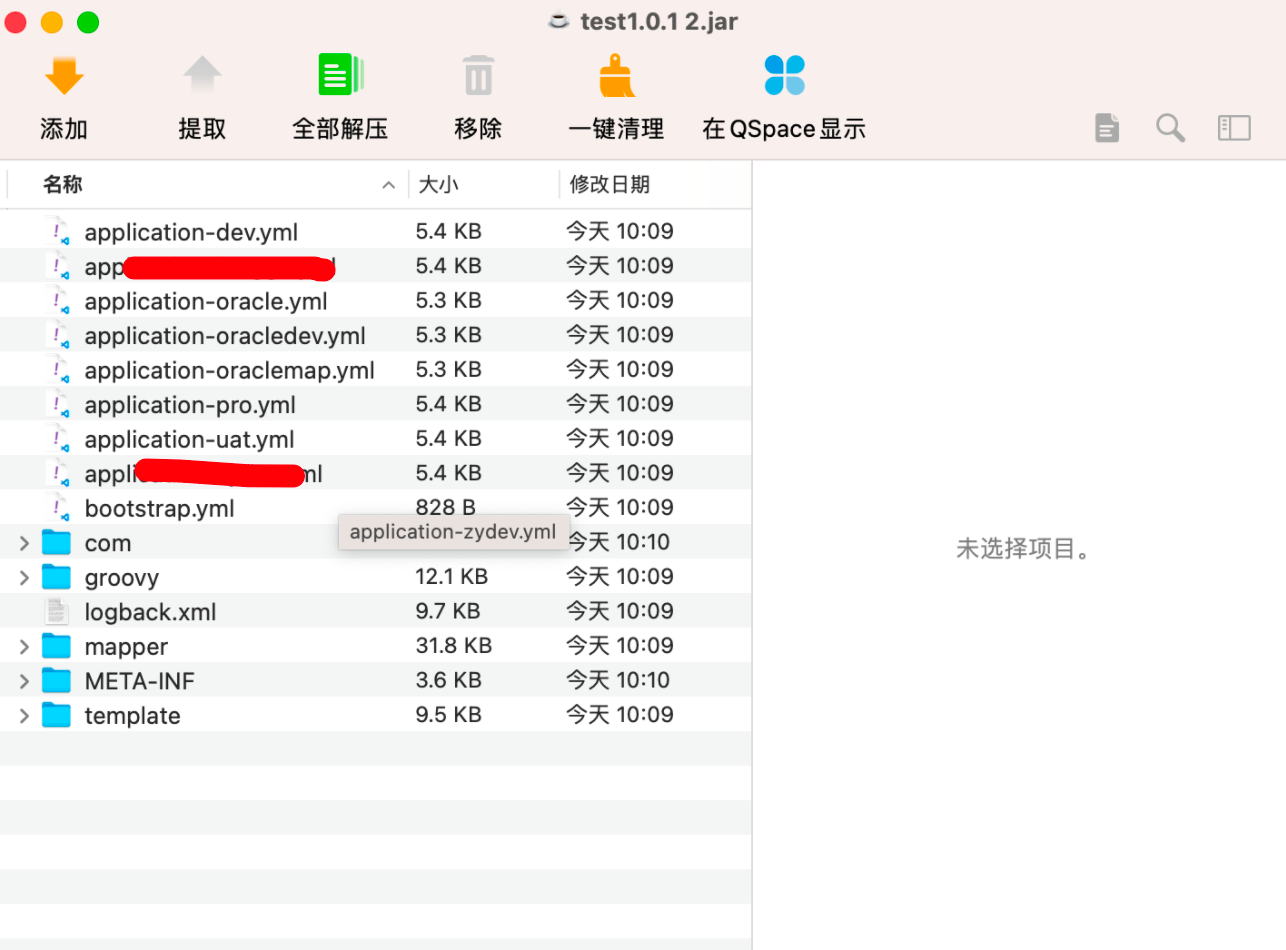
image-20231215141042141

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

🖊️最后总结

🖲要熟练掌握技巧，一定多多坚持练习：骐骥一跃，不能十步；驽马十驾，功在不舍。

搞笑点赞

相关文章：

maven打包插件maven-jar-plugin与spring-boot-maven-plugin

maven几种打包插件介绍 文章目录 &#x1f50a;1.spring-boot-maven-plugin打包后效果 &#x1f4d5;2.maven-jar-plugin打包后效果&#x1f58a;️最后总结 &#x1f50a;1.spring-boot-maven-plugin <plugins><plugin><groupId>org.springframework.boot&…...

编程日记 2023/12/16 5:11:04

uniapp微信小程序下载base64图片流或https图片

常规https的图片下载是这样的 const urlPath https://test/logo.png uni.downloadFile({url: urlPath,success(res){// 这时会产生一个临时路径&#xff0c;在应用本次启动期间可以正常使用。if (res.statusCode 200) {// 需要将图片保存到相册uni.saveImageToPhotosAlbum({…...

编程日记 2023/12/16 5:10:03

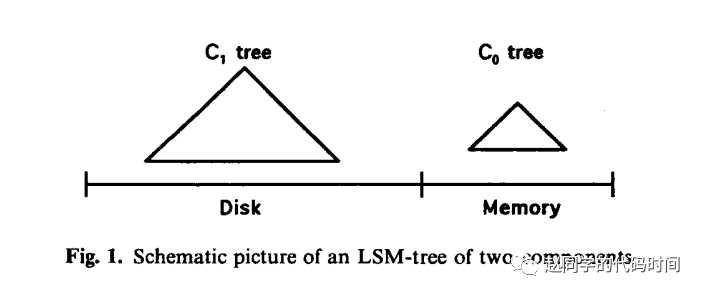
数据结构 | Log-Structured Merge Tree (LSM Tree)

今天介绍LSM Tree这个数据结构&#xff0c;严格意义上来说&#xff0c;他并不像他的名字一样是一棵树型的数据结构&#xff0c;而更多是一种设计思想。 LSM Tree最先在1996年被提出&#xff0c;后来被广泛运用于现代NoSQL&#xff08;非关系型数据库&#xff09;系统中&#xf…...

编程日记 2023/12/16 5:09:02

QEMU源码全解析 —— virtio（9）

接前一篇文章&#xff1a; 上两回讲解了virtio balloon相关类所涉及的realize函数以及大致流程&#xff0c;如下表所示&#xff1a; realize函数parent_dc_realize函数DeviceClassvirtio_pci_dc_realizePCIDeviceClassvirtio_pci_realizeVirtioPCIClassvirtio_balloon_pci_rea…...

编程日记 2023/12/16 5:08:01

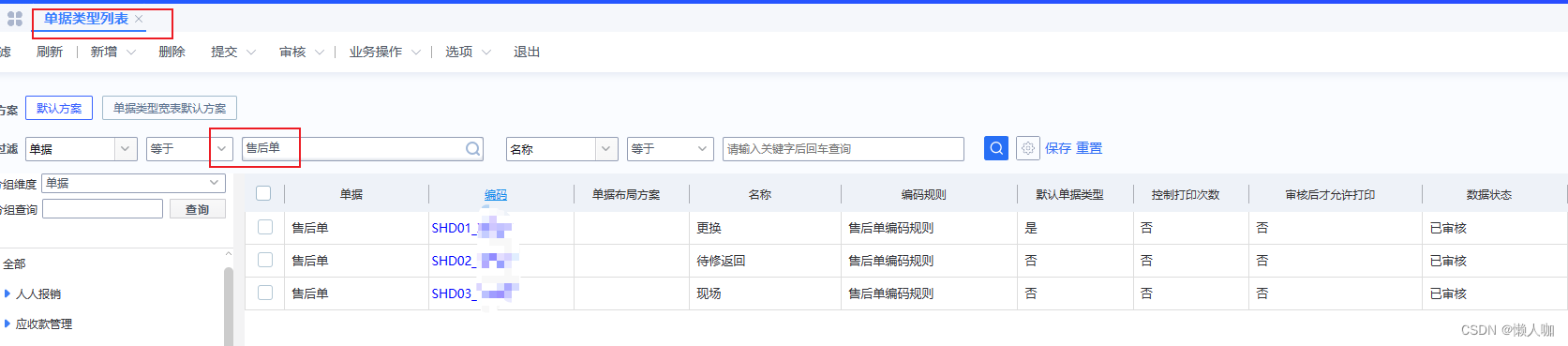
金蝶云星空协同开发环境应用内执行单据类型脚本

文章目录 金蝶云星空协同开发环境应用内执行单据类型脚本业务界面查询单据类型表数据导出数据执行数据库脚本单据类型xml检验是否执行成功检查数据库检查业务数据 金蝶云星空协同开发环境应用内执行单据类型脚本 业务界面 查询单据类型表数据 先使用类型中文在单据类型多语言…...

编程日记 2023/12/16 5:07:00

矩阵理论及其应用邱启荣习题3.5题解

(1) P ( − 1 0 1 − 1 − 1 2 1 1 − 1 ) \begin{pmatrix} -1 & 0&1 \\ -1 & -1&2\\1&1&-1 \end{pmatrix} ​−1−11​0−11​12−1​ ​ A ( 1 0 1 1 1 0 − 1 2 1 ) \begin{pmatrix} 1 & 0&1 \\ 1 & 1&0\\-1&2&1 \end{pmat…...

编程日记 2023/12/16 5:04:59

Java面试题（每天10题）-------连载（49）

目录 Tomcat篇 1、Tomcat的缺省端口是多少&#xff1f;怎么修改&#xff1f; 2、Tomcat有哪几种Connector运行模式&#xff08;优化&#xff09;&#xff1f; 3、Tomcat有几种部署方式&#xff1f; 4、Tomcat容器时如何创建servlet类实例&#xff1f;用到了什么原理&…...

编程日记 2023/12/16 5:03:58

python——数据类型

数据类型目录 前言一、Number（数字）数字类型转换：二、String（字符串）常用字符串运算符：字符串格式化：三、Tuple（元组）常用运算符四、List（列表）嵌套列表：常用列表操作：五、Dictionary（字典）六、Set（集合）...

编程日记 2023/12/16 5:01:57

hive中如何求取中位数？

目录 中位数的概念代码实现准备数据实现 中位数的概念 中位数&#xff08;Median&#xff09;又称中值&#xff0c;统计学中的专有名词&#xff0c;是按顺序排列的一组数据中居于中间位置的数&#xff0c;代表一个样本、种群或概率分布中的一个数值&#xff0c;其可将数值集合…...

编程日记 2023/12/16 5:00:55

在C#中异步编程

在C#中&#xff0c;异步编程是一种编写并发和响应式代码的技术&#xff0c;通过将耗时的操作放在后台线程中执行&#xff0c;以避免阻塞主线程&#xff0c;提高程序的性能和响应性。异步编程使用async和await关键字&#xff0c;结合任务&#xff08;Task&#xff09;和异步操作…...

编程日记 2023/12/16 4:59:54

微服务保护--Feign整合Sentinel

限流是一种预防措施&#xff0c;虽然限流可以尽量避免因高并发而引起的服务故障&#xff0c;但服务还会因为其它原因而故障。而要将这些故障控制在一定范围&#xff0c;避免雪崩&#xff0c;就要靠线程隔离&#xff08;舱壁模式&#xff09;和熔断降级手段了。 线程隔离之前讲到…...

编程日记 2023/12/16 4:58:54

二进制to十六进制

输入小于等于十六位的二进制数据&#xff0c;输出十六进制数据&#xff1b; #include <stdio.h> #include <stdlib.h> #include <math.h>int main(void) {char arr[16] { 0 }; int array[16] { 0 }; int hex[4] { 0 };int i 0; int num 0;scanf("…...

编程日记 2023/12/16 4:57:53

Logistic 回归算法

Logistic 回归 Logistic 回归算法Logistic 回归简述Sigmoid 函数Logistic 回归模型表达式求解参数 $\theta $梯度上升优化算法 Logistic 回归简单实现使用 sklearn 构建 Logistic 回归分类器Logistic 回归算法的优缺点 Logistic 回归算法 Logistic 回归简述 Logistic 回归是一…...

编程日记 2023/12/16 4:56:52

ubuntu安装详细步骤

一&#xff0c;先下载vmware 1&#xff0c;第一步打开上面链接 下载网址 : https://www.vmware.com/products/workstation-pro/wo rkstation-pro-evaluation.html 许可证 JU090-6039P-08409-8J0QH-2YR7F ZF3R0-FHED2-M80TY-8QYGC-NPKYF FC7D0-D1YDL-M8DXZ-CYPZE-P2AY6 ZC3T…...

编程日记 2023/12/16 4:54:50

力扣5. 最长回文子串

动态规划 思路&#xff1a; 假设 dp[i][j] 为字符串 (i, j) 子串是否为回文的结果&#xff1b;那么 dp[i][j] dp[i 1][j - 1] 且 (s[i] s[j])&#xff1b;长度为1的字符串都是回文&#xff1b; 原字符串长度为1&#xff0c;是回文&#xff1b;原字符串子串长度为1&#xff…...

编程日记 2023/12/16 4:53:49

肆[4]，函数VectorToHomMat2d/AffineTransPoint2d

函数VectorToHomMat2d C形式 LIntExport void VectorToHomMat2d( const HTuple& Px, const HTuple& Py, const HTuple& Qx, const HTuple& Qy, HTuple* HomMat2D);//参数1:图像坐标X数组 //参数2:图像坐标Y数组 //参数3:世界坐标X数组 //参数4:世界坐标Y…...

编程日记 2023/12/16 4:52:48

下载文件 后端返回给前端 response header 响应头

当浏览器在请求资源时&#xff0c;会通过http返回头中的content-type决定如何显示/处理将要加载的数据&#xff0c;如果这个类型浏览器能够支持阅览&#xff0c;浏览器就会直接展示该资源&#xff0c;比如png、jpeg、video等格式。在某些下载文件的场景中&#xff0c;服务端可能…...

编程日记 2023/12/16 4:51:47

lvs负载均集群

目录 NAT模式 LVS负载均衡群集部署 1.部署共享存储 2.配置节点服务器 192.168.17.130 ​编辑 192.168.17.133 3.配置负载调度器 4.测试效果 NAT模式 LVS负载均衡群集部署 负载调度器&#xff1a;内网关 ens33&#xff1a;192.168.17.70&#xff0c;外网关 ens36&#x…...

编程日记 2023/12/16 4:50:46

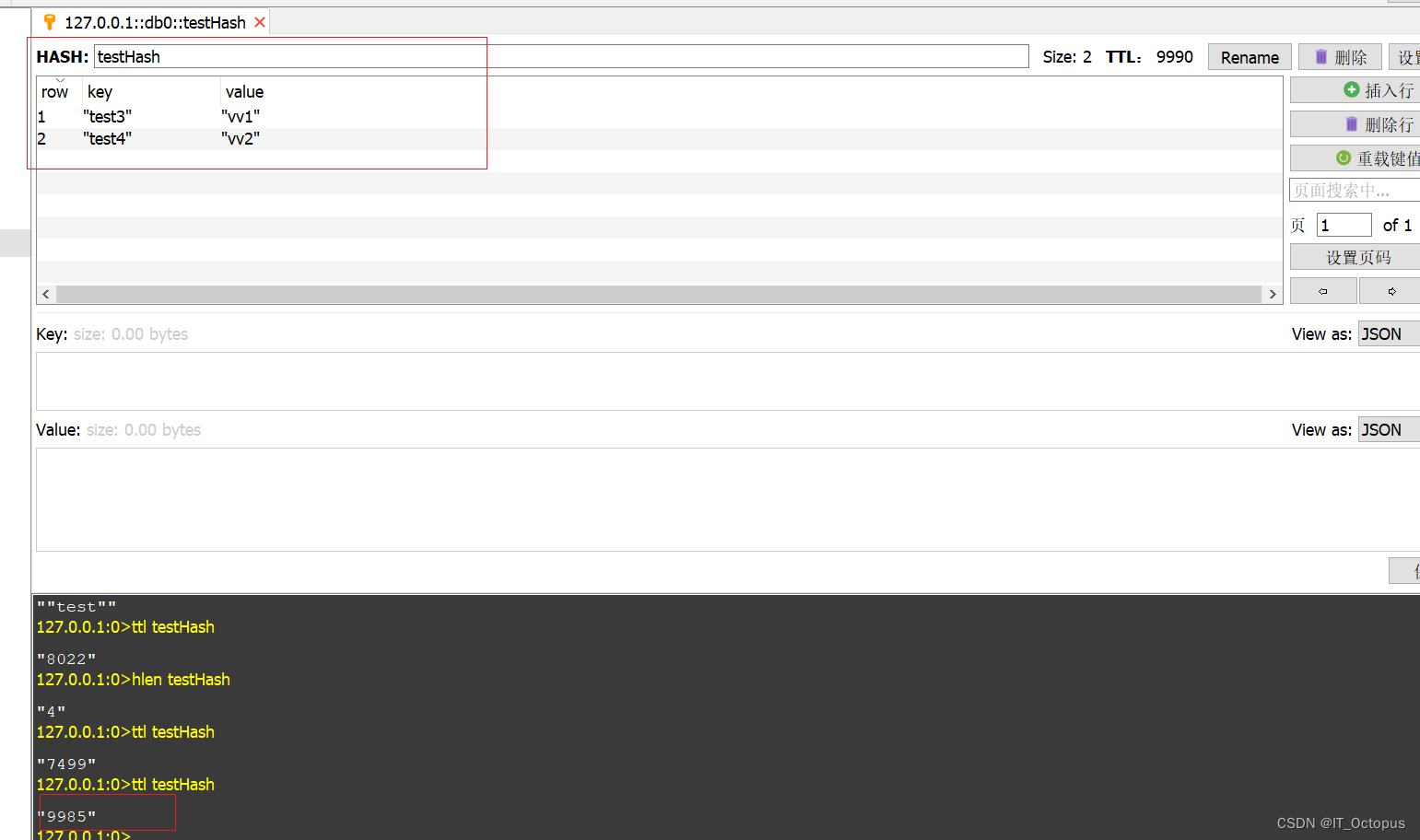
luttuce(RedisTempate)实现hash expire lua脚本

话不多说先放脚本&#xff1a; local argv ARGV local length #argv if length > 0 then local unpackArgs {} for i 1, length - 1 dotable.insert(unpackArgs, argv[i]) end if redis.call(exists, KEYS[1]) 1 thenredis.call(del, KEYS[1])redis.call(hset, KEYS[…...

编程日记 2023/12/16 4:49:45

【Xamarin】WebView连接局域网自动跳转外部浏览器问题的解决

xamarin在中国用的很少&#xff0c;但也有一些独到之处。例如用惯了Visual Studio的就很合适。而且类Java开发&#xff0c;几乎没什么障碍。 protected override void OnCreate(Bundle savedInstanceState) {base.OnCreate(savedInstanceState);Xamarin.Essentials.Platform.I…...

编程日记 2023/12/16 4:48:44

网络编程（Modbus进阶）

思维导图 Modbus RTU&#xff08;先学一点理论&#xff09; 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议&#xff0c;由 Modicon 公司&#xff08;现施耐德电气&#xff09;于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

编程新知 2026/2/7 23:18:34

AI-调查研究-01-正念冥想有用吗？对健康的影响及科学指南

点一下关注吧&#xff01;&#xff01;&#xff01;非常感谢&#xff01;&#xff01;持续更新&#xff01;&#xff01;&#xff01; &#x1f680; AI篇持续更新中&#xff01;&#xff08;长期更新&#xff09; 目前2025年06月05日更新到&#xff1a; AI炼丹日志-28 - Aud…...

编程新知 2026/2/8 5:11:39

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录

ASP.NET Core 是一个跨平台的开源框架&#xff0c;用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录&#xff0c;以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

编程新知 2026/2/8 4:37:06

Opencv中的addweighted函数

一.addweighted函数作用 addweighted&#xff08;&#xff09;是OpenCV库中用于图像处理的函数&#xff0c;主要功能是将两个输入图像&#xff08;尺寸和类型相同&#xff09;按照指定的权重进行加权叠加&#xff08;图像融合&#xff09;&#xff0c;并添加一个标量值&#x…...

编程新知 2026/2/1 1:50:03

镜像里切换为普通用户

如果你登录远程虚拟机默认就是 root 用户&#xff0c;但你不希望用 root 权限运行 ns-3&#xff08;这是对的&#xff0c;ns3 工具会拒绝 root&#xff09;&#xff0c;你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案&#xff1a;创建非 roo…...

编程新知 2025/9/11 11:00:29

第一篇：Agent2Agent (A2A) 协议——协作式人工智能的黎明

AI 领域的快速发展正在催生一个新时代&#xff0c;智能代理&#xff08;agents&#xff09;不再是孤立的个体&#xff0c;而是能够像一个数字团队一样协作。然而&#xff0c;当前 AI 生态系统的碎片化阻碍了这一愿景的实现&#xff0c;导致了“AI 巴别塔问题”——不同代理之间…...

编程新知 2026/1/31 3:30:33

linux 下常用变更-8

1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行&#xff0c;YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID&#xff1a; YW3…...

编程新知 2025/10/7 15:08:22

鱼香ros docker配置镜像报错：https://registry-1.docker.io/v2/

使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题&#xff1a;docker pull 失败 网络不同&#xff0c;需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

编程新知 2025/12/31 6:28:08

SpringTask-03.入门案例

一.入门案例 启动类&#xff1a; package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

编程新知 2026/2/2 0:35:08

第 86 场周赛：矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词

Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵&#xff0c;其中每行&#xff0c;每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid&#xff0c;其中有多少个 3 3 的 “幻方” 子矩阵&am…...

编程新知 2026/2/7 13:27:36