VUE-脚手架搭建
文章目录
- 一、概述
- 二、前提准备
- 1. 安装 node-js
- 2. npm 镜像设置
- 3. 安装 vs-code
- 三、脚手架搭建
- 1. Vue-2 搭建
- 1. Vue-3 搭建
一、概述
官网:http://cn.vuejs.org/
vue 有两个大版本,分别是 vue-2 和 vue-3,目前新项目的话用 vue-3 的会比较多
vue-2 官方文档:https://v2.cn.vuejs.org/v2/guide/installation.html
vue-3 官方文档:https://cn.vuejs.org/guide/introduction.html
以下我会分别提供搭建 vue-2 和 vue-3 脚手架的过程。
二、前提准备
1. 安装 node-js
为什么要下载 node-js ?
node 提供了 Javascript 的运行环境,可以让 Javascript 运行在服务端的开发平台
node-js 下载:https://nodejs.org/en/download/
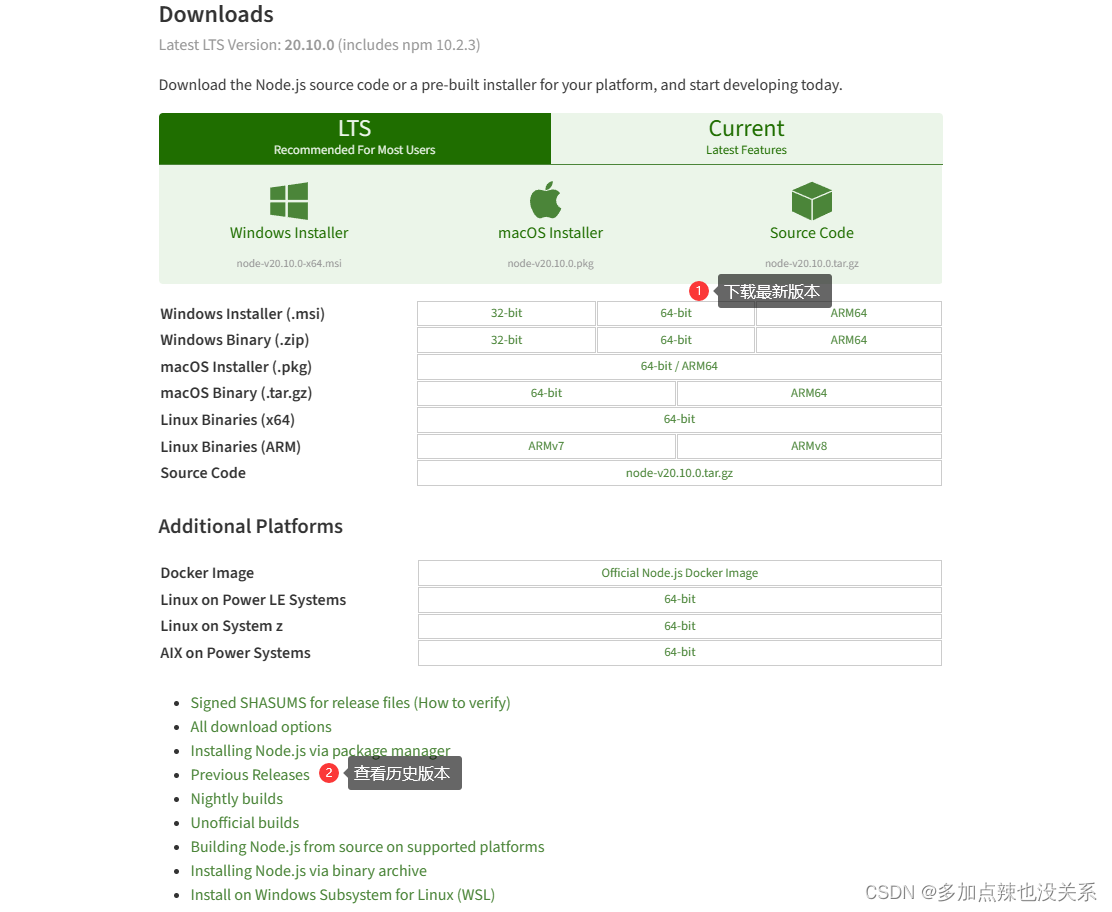
一般会选择在 LTS 下进行下载,因为 LTS 是稳定版本的,然后根据自己电脑的系统选择安装,比方说我电脑是 windows-64x 的,那我就点击 Windows Installer(.msi) > 64-bit 就会开始下载

如果想要下载旧版本可在 Previous Release 中查询
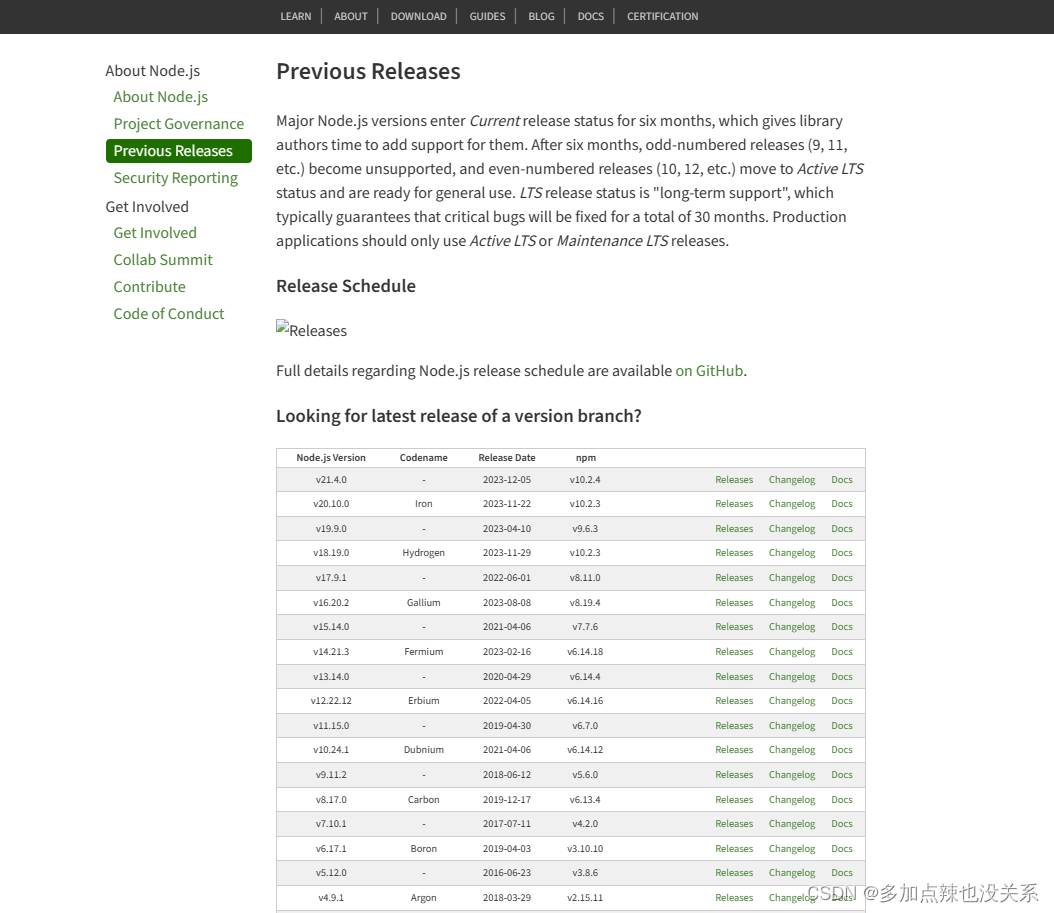
点击 Releases 就能跳转到对应的下载界面
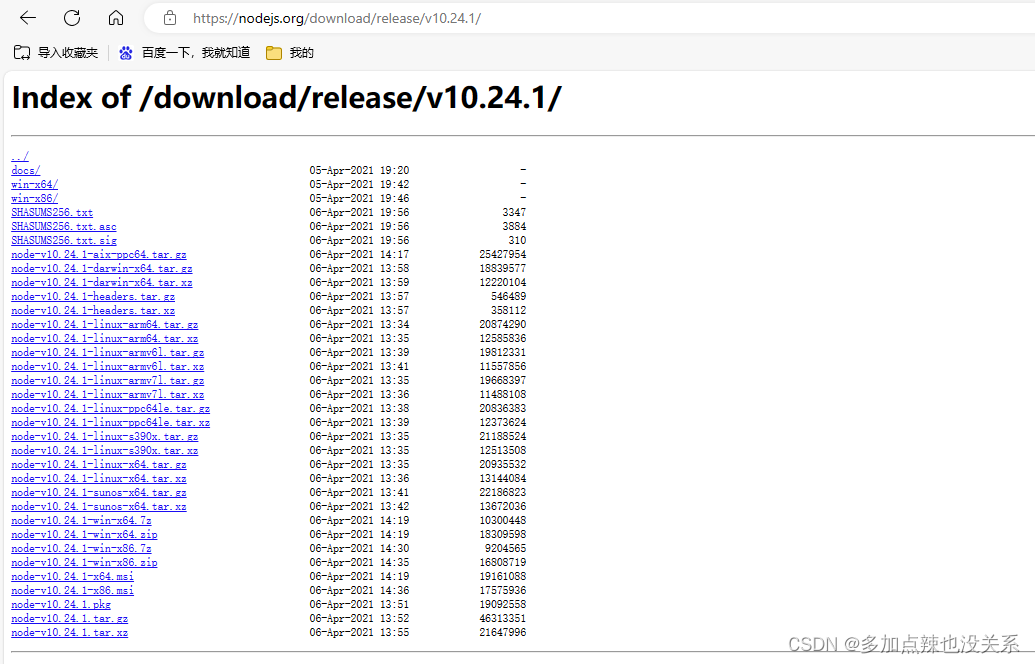
或者直接在地址上面输入,点击 enter 也能获取
PS:建议 node-js 的版本最好在 16 以上
点击对应的包即可下载完成

下载好安装程序包之后,只需要双击打开即可进行安装

node 的安装也是傻瓜式的,一直 next 即可

然后点击 finsh
检测 node-js 是否安装成功,只需要 win + R 调起 运行命令框,输入 cmd 打开 cmd窗口,再输入 node -v 查看 node 的版本,如果有显示版本信息,就表明 node-js 安装成功了

npm 是 node-js 的包管理和分发工具,当安装完成 node-js 后 npm 也随之安装完成,可以通过 npm -v 来校验是否安装成功

2. npm 镜像设置
在 vue 中经常会使用 npm 来安装一些包,而 npm 的下载镜像是在国外,所以使用 npm 下载会非常的慢,这里有两种方式来解决这个问题:
-
方式一:使用
yarn进行安装使用
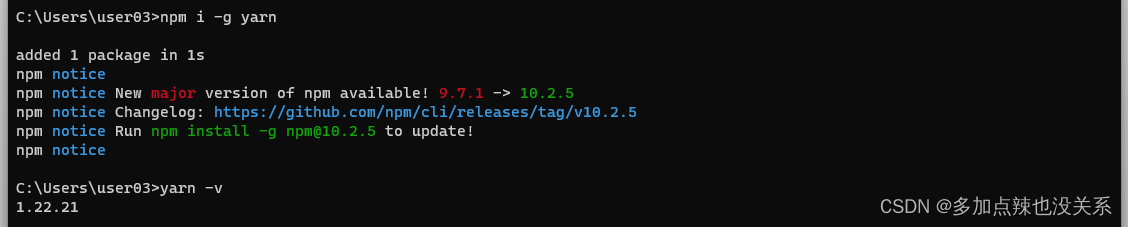
yarn安装就需要保证当前系统有下载过yarn,同样可以在cmd窗口中输入yarn -v来检测是否安装过yarn

如果没有就下载,输入:npm i -g yarn,下载完成之后仍旧可以输入yarn -v来进行检测
-
方式二:设置
npm镜像为国内的
可以在cmd窗口中通过npm config get registry命令来查询npm所使用的镜像

默认使用的镜像是:https://registry.npmjs.org/,如果你 npm 所使用的镜像是这个的话,就换成国内的,比如:
(1)https://registry.npm.taobao.org/
(2)https://registry.npmmirror.com
比如我使用 https://npmmirror.com/ 所提供的镜像 https://registry.npmmirror.com
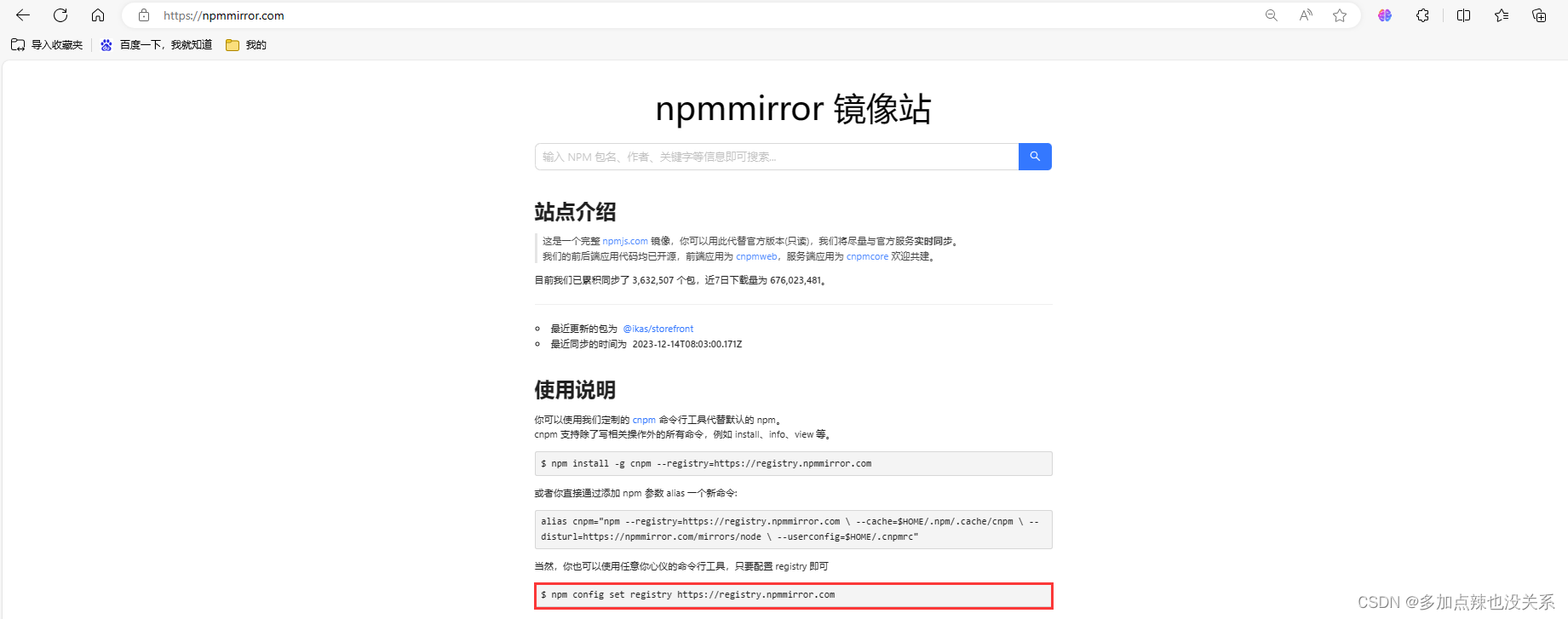
那就可以通过npm config set registry https://registry.npmmirror.com这行命令将镜像设置为 https://registry.npmmirror.com 即可

3. 安装 vs-code
vue 推荐使用 Visual Studio Code 作为编辑器,如果你之前用的是其它的编辑器进行开发,建议换成 vs-code

Visual Studio Code 下载:https://code.visualstudio.com/Download
这个安装就不多做演示了
三、脚手架搭建
1. Vue-2 搭建
(一)安装 vue-cli:
vue-cli 就是 Vue 的脚手架
vue-cli 官方文档:https://cli.vuejs.org/zh/guide/
可以看到目前 vue-cli 已经处于 维护模式 了,但并不影响对它的使用
从官方文档上可以看到安装 vue-cli 可以执行以下任一命令即可:
npm install -g @vue/cli
或者
yarn global add @vue/cli
例如:在 终端窗口 输入 npm install -g @vue/cli 进行安装
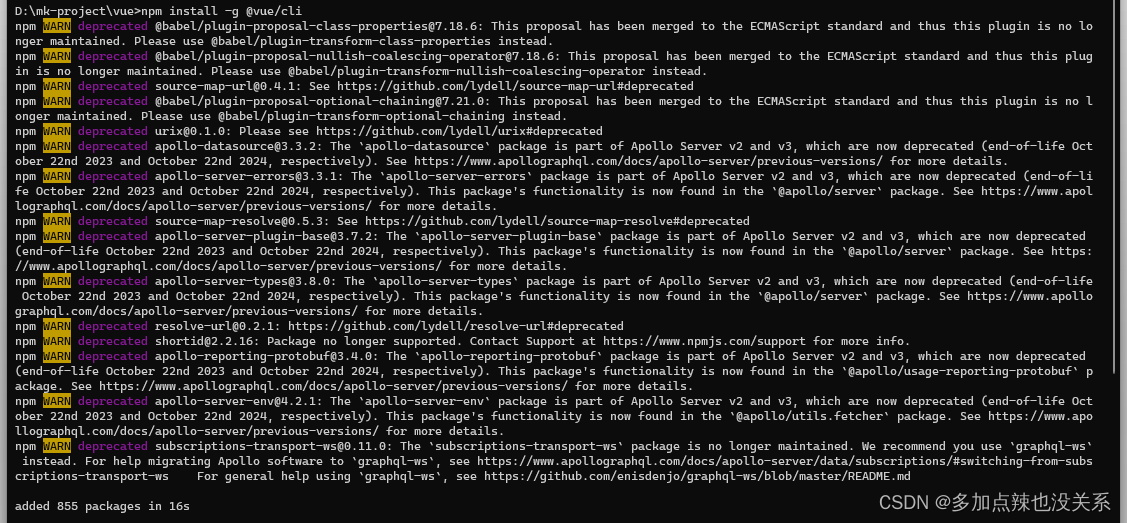
可以通过 vue --version 查看是否安装成功

如果能看到版本信息就表明安装成功
升级
vue-cli
- 如果是通过
npm install -g @vue/cli进行安装的,那么就用npm update -g @vue/cli进行升级- 如果是通过
yarn global add @vue/cli进行安装的,那么就用yarn global upgrade --latest @vue/cli进行卸载
卸载
vue-cli
- 如果是通过
npm install -g @vue/cli进行安装的,那么就用npm uninstall -g @vue/cli进行卸载- 如果是通过
yarn global add @vue/cli进行安装的,那么就用yarn global remove @vue/cli进行卸载
(二)搭建脚手架:
可以建一个空白文件夹来存放项目,在该文件夹下调出 终端窗口

然后输入以下命令创建项目
vue create <product-name>
<product-name> 表示创建项目的名称,值得注意的是 项目名称不能出现大写字母,如:myApp
例如:创建一个名为 my-vue2 的项目
输入 vue create my-vue2 命令,现在默认是创建 vue-3 的脚手架,可以通过 ↑ ↓ 键来选择所需创建 vue 脚手架的版本,这里我就选择 Default([Vue 2] bale, eslint)
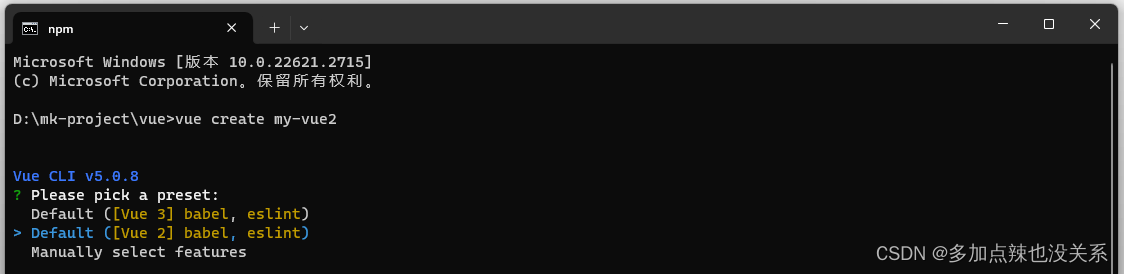
选择之后点击 enter 就会开始自动搭建
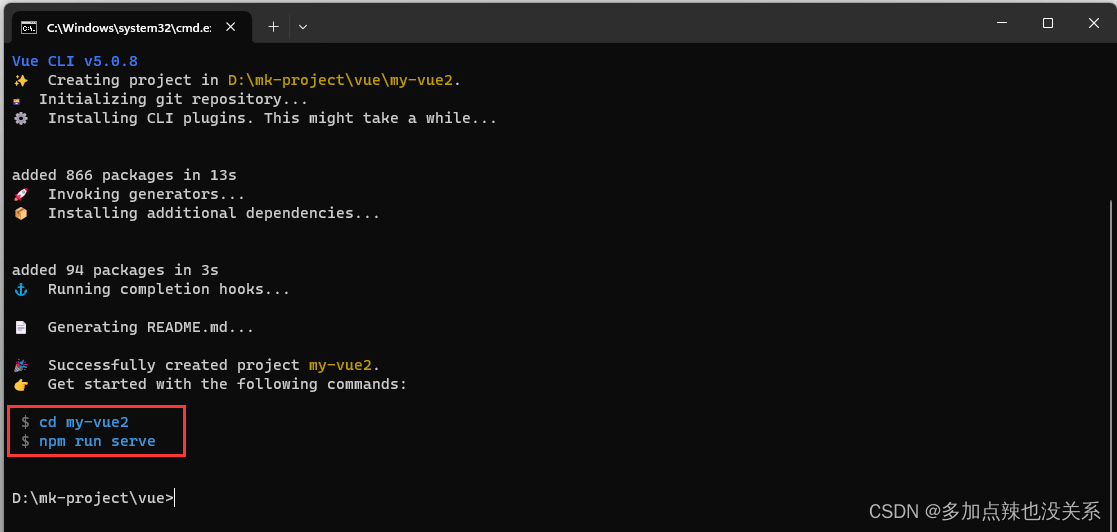
到这里 vue-2 的脚手架就已经搭建完成了,可以将创建完成的项目在 vs-code 当中打开
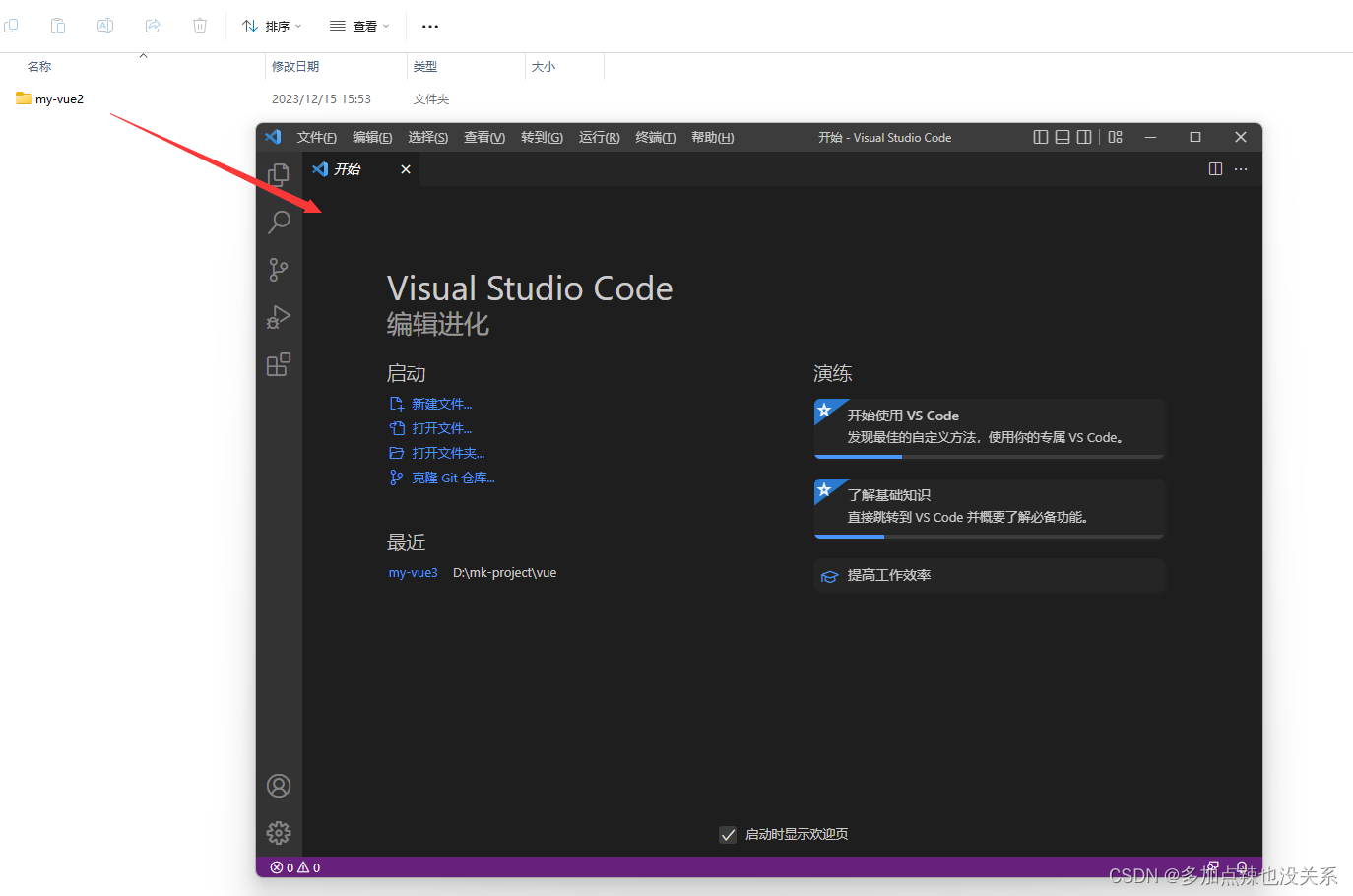
新建一个终端,输入 npm run serve 命令运行项目即可
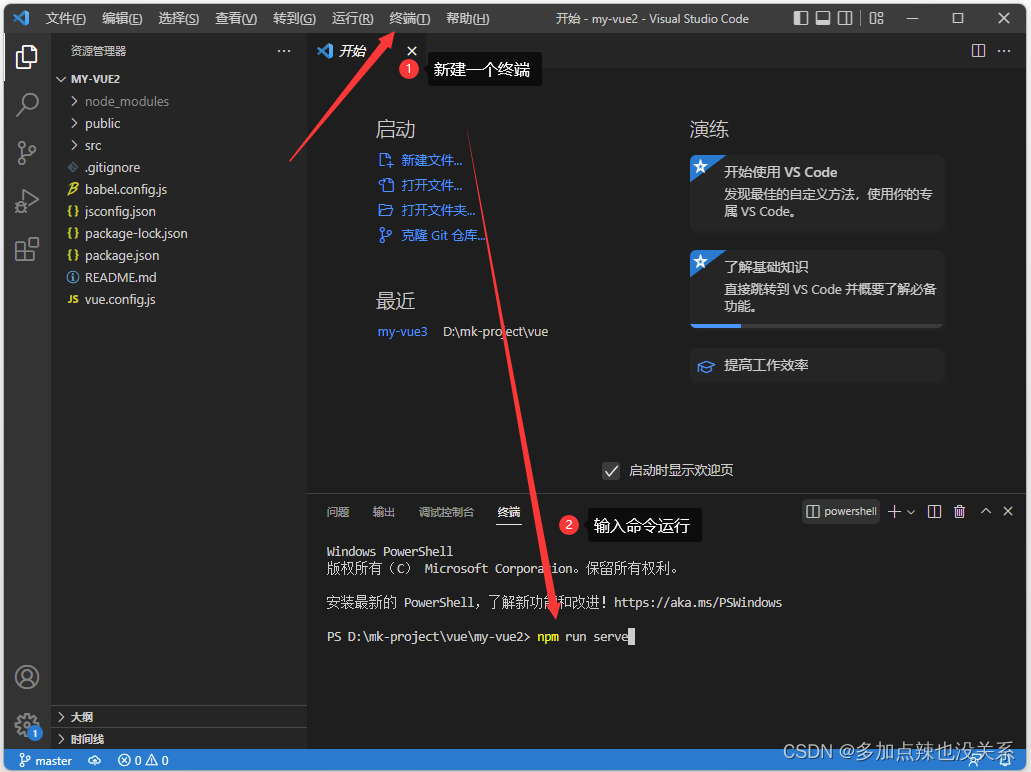
控制台输入以下内容,表示成功

可以复制链接到游览器上查看:http://localhost:8080/

1. Vue-3 搭建
方式一:
可以继续像 vue-2 搭建脚手架那种方式进行搭建,下载 vue-cli,只不过选择 Default([Vue 3] bale, eslint)
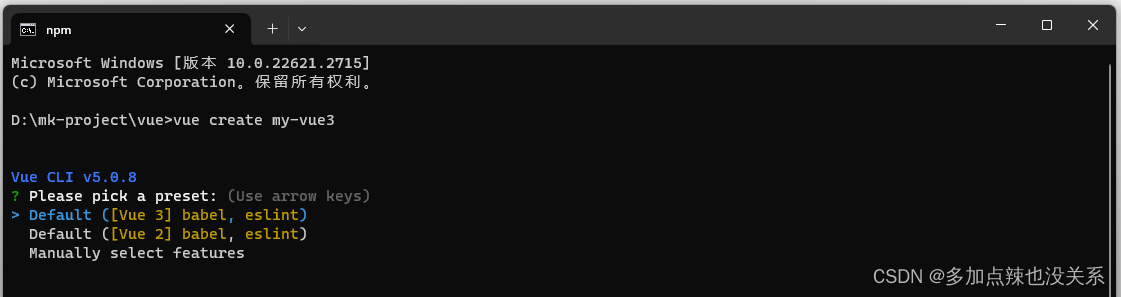
其余步骤与 vue-2 搭建脚手架的步骤一样,就不多做赘述
方式二:
从官方文档中可知

使用 vue-3 ,node-js 的版本最好是在 16.0 以上
创建 vue-3 的脚手架不需要安装 vue-cli,只需要输入以下命令即可:
npm create vue@latest
例如:创建一个名为 my-vue3 的项目
在一个空白的文件夹下调出 终端窗口

输入 npm create vue@latest 命令,接着输入项目名称 <your project-name> ,然后一直按 enter 直至结束,就能创建成功
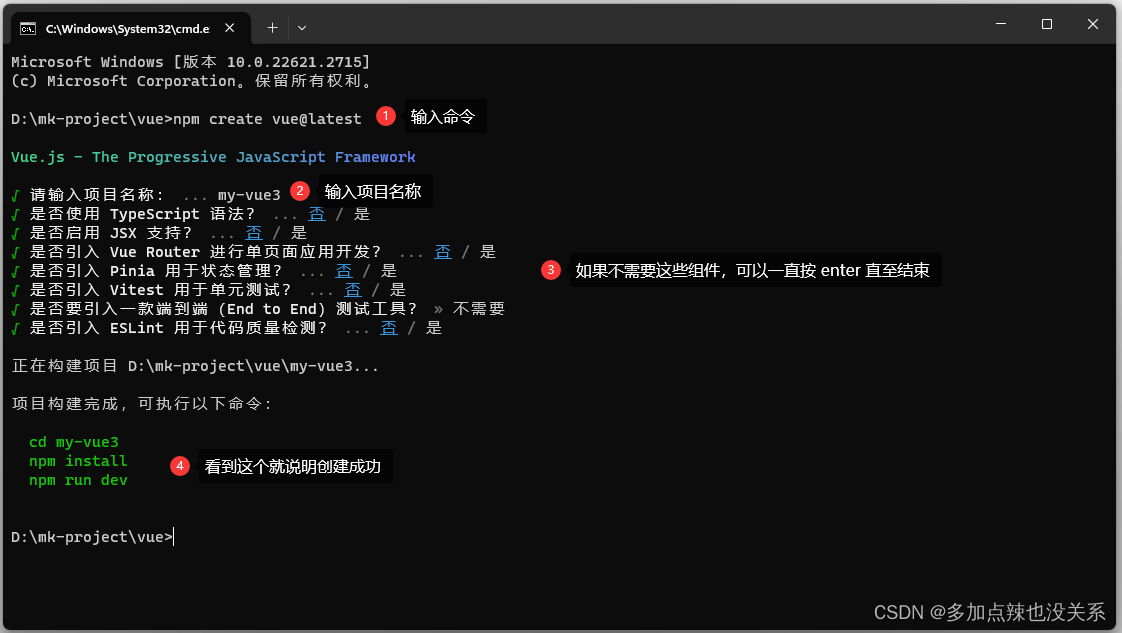
同样也可以将创建好的项目拖动到 vs-code 中
打卡终端工具,先输入 npm install 安装一些必要的包,再 npm run serve 运行即可
可以复制链接到游览器上查看:http://127.0.0.1:5173/
相关文章:

VUE-脚手架搭建
文章目录 一、概述二、前提准备1. 安装 node-js2. npm 镜像设置3. 安装 vs-code 三、脚手架搭建1. Vue-2 搭建1. Vue-3 搭建 一、概述 官网:http://cn.vuejs.org/ vue 有两个大版本,分别是 vue-2 和 vue-3,目前新项目的话用 vue-3 的会比较多…...

ArcGIS Pro SDK根据Xml/Json文件反向生成几何
需求: geometry文件导出后的xml,在另一台电脑上反向生成geometry 解决方案: 点 MapPoint minPointImport MapPointBuilderEx.FromXml(xml); 线 包络线 Envelope envelopeImport EnvelopeBuilderEx.FromXml(xml); 面 var geometryB…...

LY/T 3301-2022 实木厚芯胶合板检测
实木厚芯胶合板是指按照相邻层单板木纹方向垂直组坯,通过胶黏剂将表板、中间层板和芯板黏合而成的5层或5层以上的对称结构板材。 LY/T 3301-2022实木厚芯胶合板测试: 测试项目 测试方法 静曲强度 GB/T 17657 弹性模量 GB/T 17657 含水率 GB/T 17…...

代码随想录算法训练营第十六天| 104. 二叉树的最大深度、111. 二叉树的最小深度、222. 完全二叉树的节点个数
代码随想录算法训练营第十六天| 104. 二叉树的最大深度、111. 二叉树的最小深度、222. 完全二叉树的节点个数 题目 104.二叉树的最大深度 给定一个二叉树 root ,返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。 # Defin…...

字符串——OJ题
📘北尘_:个人主页 🌎个人专栏:《Linux操作系统》《经典算法试题 》《C》 《数据结构与算法》 ☀️走在路上,不忘来时的初心 文章目录 一、字符串相加1、题目讲解2、思路讲解3、代码实现 二、仅仅反转字母1、题目讲解2、思路讲解3…...

Linux---cp和mv命令选项
1. cp命令选项 命令选项说明-i交互式提示-r递归拷贝目录及其内容-v显示拷贝后的路径描述-a保留文件的原有权限 cp -i命令选项效果图: cp -r命令选项效果图: cp -v命令选项效果图: cp -a命令选项效果图: -a选项说明: -a 选项还支持拷贝文件夹并且文件夹中的文件权限不丢失 …...

LVS负载均衡器(nat模式)+nginx(七层反向代理)+tomcat(多实例),实现负载均衡和动静分离
目录 前言 一、配置nfs共享存储 二、配置2个nginx节点服务的网页页面 节点1:192.168.20.10 步骤一:修改网关指向调度器的内网ip地址 步骤二:将nfs共享的目录进行挂载,并修改nginx的配置文件中location的root指向挂载点 步骤三ÿ…...
【深度学习】TensorFlow深度模型构建:训练一元线性回归模型
文章目录 1. 生成拟合数据集2. 构建线性回归模型数据流图3. 在Session中运行已构建的数据流图4. 输出拟合的线性回归模型5. TensorBoard神经网络数据流图可视化6. 完整代码 本文讲解: 以一元线性回归模型为例, 介绍如何使用TensorFlow 搭建模型 并通过会…...

智能插座是什么
智能插座 电工电气百科 文章目录 智能插座前言一、智能插座是什么二、智能插座的类别三、智能插座的原理总结 前言 智能插座的应用广泛,可以用于智能家居系统中的电器控制,也可以应用在办公室、商业场所和工业控制中,方便快捷地实现电器的远…...

5G工业网关视频传输应用
随着科技的不断进步,5G网络技术已经成为了当前最热门的话题之一。而其中一个引人注目的领域就是5G视频传输和5G工业网关应用。在传统网络通信中,由于带宽和延迟的限制,视频传输常常受到限制,而工业网关应用也存在着链路不稳定、数…...
Axure电商产品移动端交互原型,移动端高保真Axure原型图(RP源文件手机app界面UI设计模板)
本作品是一套 Axure8 高保真移动端电商APP产品原型模板,包含了用户中心、会员成长、优惠券、积分、互动社区、运营推广、内容推荐、商品展示、订单流程、订单管理、售后及服务等完整的电商体系功能架构和业务流程。 本模板由一百三十多个界面上千个交互元件及事件组…...

【k8s】使用Finalizers控制k8s资源删除
文章目录 词汇表基本删除操作Finalizers是什么?Owner References又是什么?强制删除命名空间参考 你有没有在使用k8s过程中遇到过这种情况: 通过kubectl delete指令删除一些资源时,一直处于Terminating状态。 这是为什么呢? 本文将…...
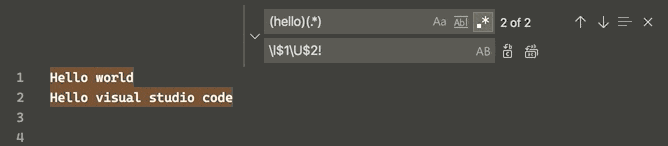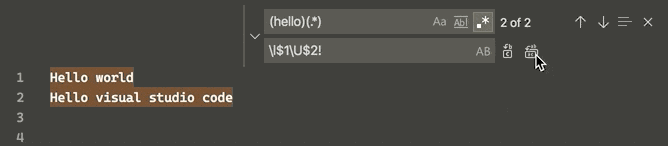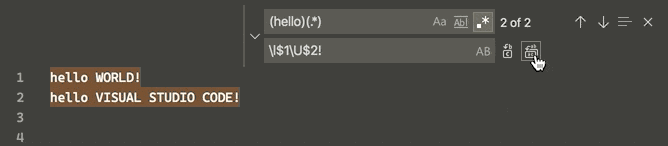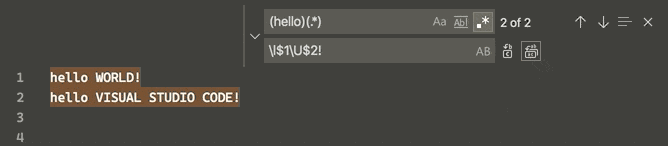
vscode
文章目录 变量引用Multi-selections(multi-cursor)Column (box) selection在正则表达式替换中改变大小写tasks.jsonlaunch.json vscode工作空间下有一个.vscode文件夹,该文件夹下放置了vscode的配置文件,主要有: settings.json : vscode的设置…...
Jrebel 在 Idea 2023.3中无法以 debug 的模式启动问题
Jrebel 在 Idea 2023.3中无法以 debug 的模式启动问题 Idea 在升级了2023.3以后,Jrebel 无法以 debug 的模式启动,找了半天,最后在插件主页的评论区找到了解决方案 特此记录一下...
)
【C++】模版初阶(初识模版)
目录 一、引言 二、函数模版 (一)函数模版的原理 (二)函数模版的实例化 1.隐式实例化 2.显式实例化 (三)模板参数的匹配原则 三、类模版 类模版的实例化 一、引言 我们在练习题目的时候总会遇到需…...

智能优化算法应用:基于差分进化算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于差分进化算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于差分进化算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.差分进化算法4.实验参数设定5.算法结果6.…...

10 种隐藏元素的 CSS 技术
10 种隐藏元素的 CSS 技术 在 Web 开发中,在许多情况下我们可能希望操纵网站上某些元素的可见性。本文将考虑各种用例,探讨使用 CSS 隐藏元素的十种不同方法。 隐藏元素的具体行为可能会根据我们的需要而有所不同。我们可能需要为隐藏元素保留空间的方…...

SQL Server数据库使用T-SQL语句简单填充
文章目录 操作步骤:1.新建数据库起名RGB2.新建表起名rgb3.添加三个列名4.点击新建查询5.填入以下T-SQL语句,点击执行(F5)6.刷新之后,查看数据 操作环境: win10 Microsoft SQL Server Management Studio 20…...
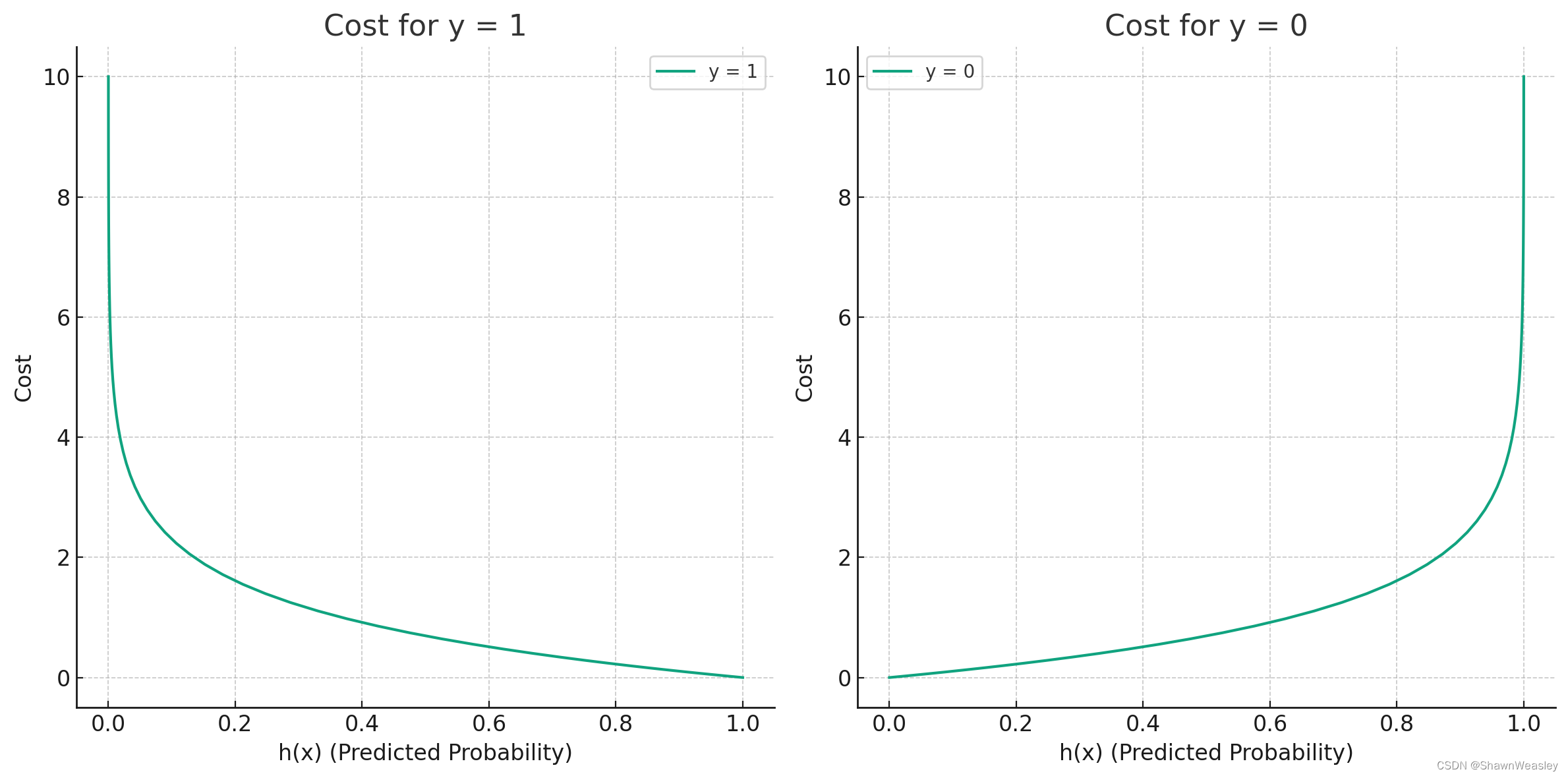
逻辑回归代价函数
逻辑回归的代价函数通常使用交叉熵损失来定义。这种损失函数非常适合于二元分类问题。 本篇来推导一下逻辑回归的代价函数。 首先,我们在之前了解了逻辑回归的定义:逻辑回归模型是一种用于二元分类的模型,其预测值是一个介于0和1之间的概率…...

芯知识 | WT2003Hx系列高品质语音芯片MP3音频解码IC的特征与应用优势
在嵌入式语音领域,唯创知音WT2003Hx系列高品质语音芯片以其卓越的音频解码性能脱颖而出。本文将深入研究该系列芯片的特色与应用优势,重点关注其支持wav、Mp3格式音频解码、高品质播放等方面。 特色一:支持wav、Mp3格式音频解码 1.多格式兼…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...
