代码随想录刷题题Day15
刷题的第十五天,希望自己能够不断坚持下去,迎来蜕变。😀😀😀
刷题语言:C++
Day15 任务
● 513.找树左下角的值
● 112. 路径总和 113.路径总和ii
● 106.从中序与后序遍历序列构造二叉树 105.从前序与中序遍历序列构造二叉树
1 找树左下角的值
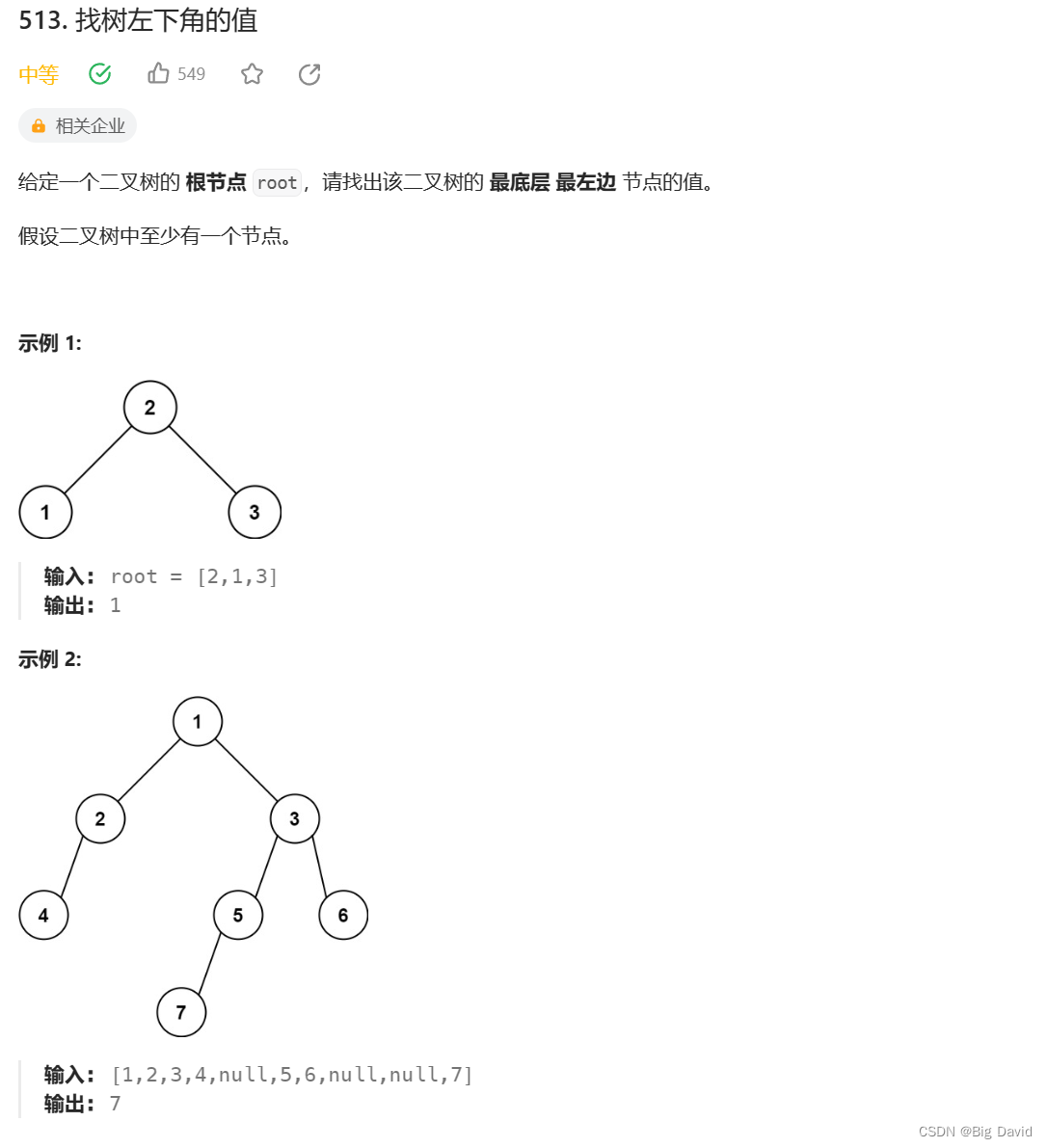
本题要找出树的最后一行最左边的值
思路1:层序遍历
思路2:递归
迭代法
层序遍历模板参考代码随想录刷题题Day12
class Solution {
public:int findBottomLeftValue(TreeNode* root) {queue<TreeNode*> que;int result;if (root != NULL) que.push(root);while (!que.empty()){int size = que.size();for (int i = 0; i < size; i++){TreeNode* node = que.front();que.pop();if (i == 0) result = node->val;// 记录最后一行第一个元素if (node->left) que.push(node->left);if (node->right) que.push(node->right);}}return result;}
};
递归法
误区:不是一直向左遍历,最后一个就是答案
一直向左遍历到最后一个,未必是最后一行
关键:在树的最后一行找到最左边的值
(1) 判断最后一行:深度最大的叶子节点
(2) 最左边的值:可以使用前序遍历(当然中序,后序都可以,因为本题没有 中间节点的处理逻辑,只要左优先就行),保证优先左边搜索,然后记录深度最大的叶子节点,此时就是树的最后一行最左边的值。
(1)确定递归函数的参数和返回值
参数:要遍历的树的根节点,最长深度
返回值:void
int maxDepth = INT_MIN;// 全局变量 记录最大深度
int result; // 全局变量 最大深度最左节点的数值
void traversal(TreeNode* node, int depth)
(2)确定终止条件
当遇到叶子节点的时候,就需要统计一下最大的深度了,所以需要遇到叶子节点来更新最大深度。
if (node->left == NULL && node->right == NULL)
{if (depth > maxDepth){maxDepth = depth; // 更新最大深度result = node->val; // 最大深度最左面的数值}return;
}
(3)确定单层递归的逻辑
找最大深度的时候,递归的过程中依然要使用回溯
// 中
if (node->left) {// 左depth++;// 深度加一traversal(node->left, depth);depth--;// 回溯,深度减一
}
if (node->right) {// 右depth++;// 深度加一traversal(node->right, depth);depth--;// 回溯,深度减一
}
C++:
class Solution {
public:int maxDepth = INT_MIN;int result;void traversal(TreeNode* node, int depth) {if (node->left == NULL && node->right == NULL) {if (maxDepth < depth) {maxDepth = depth;result = node->val;}}if (node->left) {depth++;traversal(node->left, depth);depth--;}if (node->right) {depth++;traversal(node->right, depth);depth--;}return;}int findBottomLeftValue(TreeNode* root) {traversal(root, 0);return result;}
};
精简版本C++:
class Solution {
public:int maxDepth = INT_MIN;int result;void traversal(TreeNode* node, int depth) {if (node->left == NULL && node->right == NULL) {if (maxDepth < depth) {maxDepth = depth;result = node->val;}}if (node->left) {traversal(node->left, depth + 1);// 隐藏着回溯}if (node->right) {traversal(node->right, depth + 1);// 隐藏着回溯}return;}int findBottomLeftValue(TreeNode* root) {traversal(root, 0);return result;}
};
2 路径总和
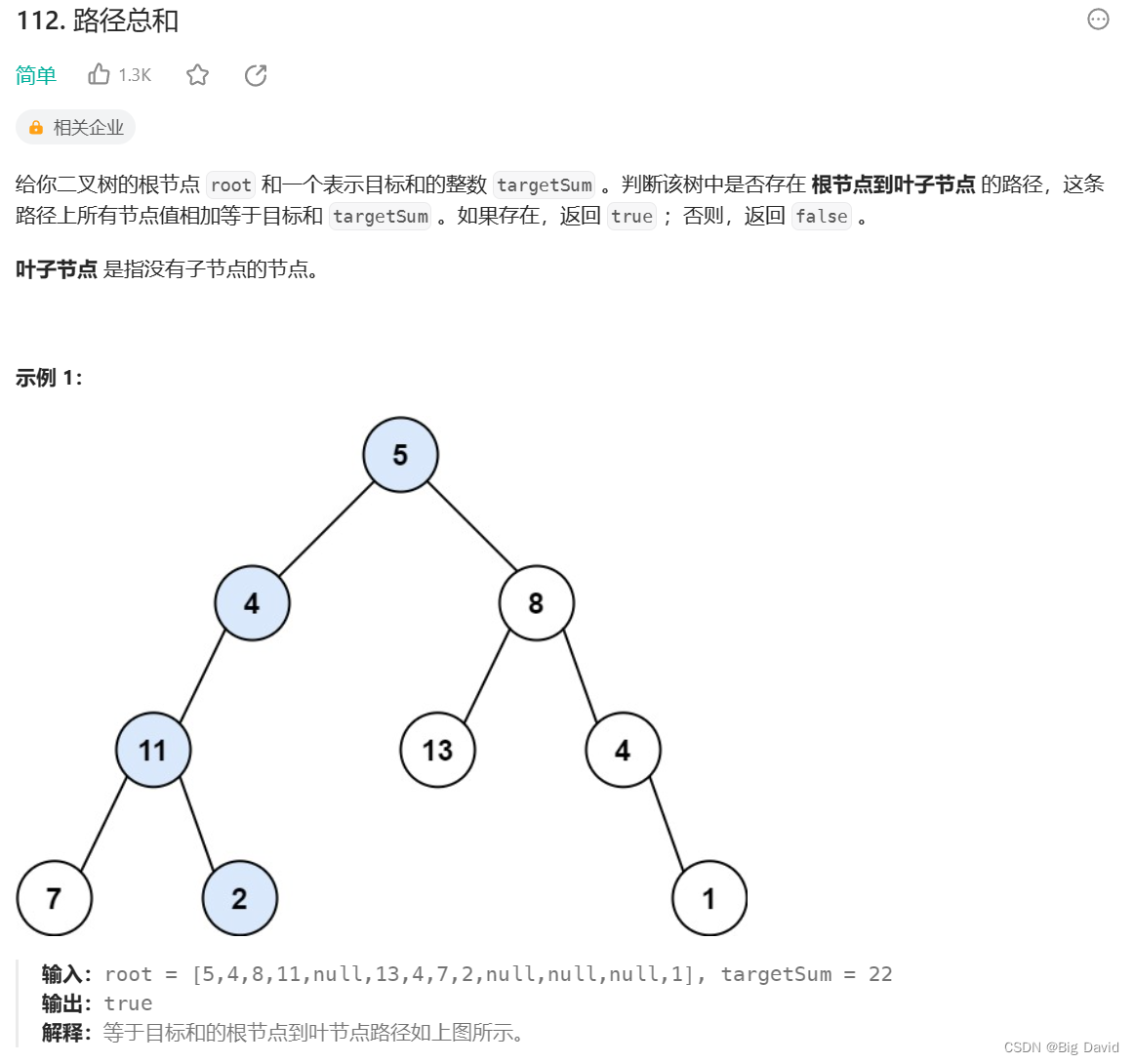
思路:
使用深度优先遍历的方式,本题前中后序都可以,因为中间节点没有处理逻辑
递归法
(1)确定递归函数的参数和返回类型
参数:二叉树的根节点、计算器(用来计算二叉树的一条边之和是否正好是目标和)
返回值:要找一条符合条件的路径,所以递归函数需要返回值,遍历的路线,并不要遍历整棵树,及时返回,返回类型是bool
递归函数返回值:
(1)如果需要搜索整棵二叉树且不用处理递归返回值,递归函数就不要返回值
(2)如果需要搜索整棵二叉树且需要处理递归返回值,递归函数就需要返回值。
(3)如果要搜索其中一条符合条件的路径,那么递归一定需要返回值,因为遇到符合条件的路径了就要及时返回
bool traversal(TreeNode* node, int count)
(2)确定终止条件
计数器count初始为目标和,然后每次减去遍历路径节点上的数值
- 如果最后count == 0,同时到了叶子节点的话,说明找到了目标和
- 如果遍历到了叶子节点,count不为0,就是没找到
if (node->left == NULL && node->right == NULL && count == 0) return true;
if (node->left == NULL && node->right == NULL && count != 0) return false;
(3)确定单层递归的逻辑
递归函数是有返回值的,如果递归函数返回true,说明找到了合适的路径,应该立刻返回
if (node->left) {// 左 (空节点不遍历)// 遇到叶子节点返回true,则直接返回trueif (traversal(node->left, count - node->left->val)) return true;
}
if (node->right) {// 右 (空节点不遍历)// 遇到叶子节点返回true,则直接返回trueif (traversal(node->right, count - node->right->val)) return true;
return false;
把回溯的过程表现出来:
if (node->left) {// 左count -= node->left->val;// 递归,处理节点;if (traversal(node->left, count)) return true;count += node->left->val;// 回溯,撤销处理结果
}
if (node->right) { // 右count -= node->right->val;if (traversal(node->right, count)) return true;count += node->right->val;// 回溯,撤销处理结果
}
C++:
class Solution {
public:bool traversal(TreeNode* node, int count) {if (node->left == NULL && node->right == NULL && count == 0) return true;// 遇到叶子节点,并且计数为0if (node->left == NULL && node->right == NULL && count != 0) return false;// 遇到叶子节点直接返回if (node->left) {// 左count -= node->left->val;// 递归,处理节点;if (traversal(node->left, count)) return true;count += node->left->val;// 回溯,撤销处理结果}if (node->right) {// 右count -= node->right->val;// 递归,处理节点if (traversal(node->right, count)) return true;count += node->right->val;// 回溯,撤销处理结果}return false;}bool hasPathSum(TreeNode* root, int targetSum) {if (root == NULL) return false;return traversal(root, targetSum - root->val);}
};
精简版本C++:
class Solution {
public:bool hasPathSum(TreeNode* root, int targetSum) {if (!root) return false;if (!root->left && !root->right && targetSum == root->val) {return true;}return hasPathSum(root->left, targetSum - root->val) || hasPathSum(root->right, targetSum - root->val);}
};
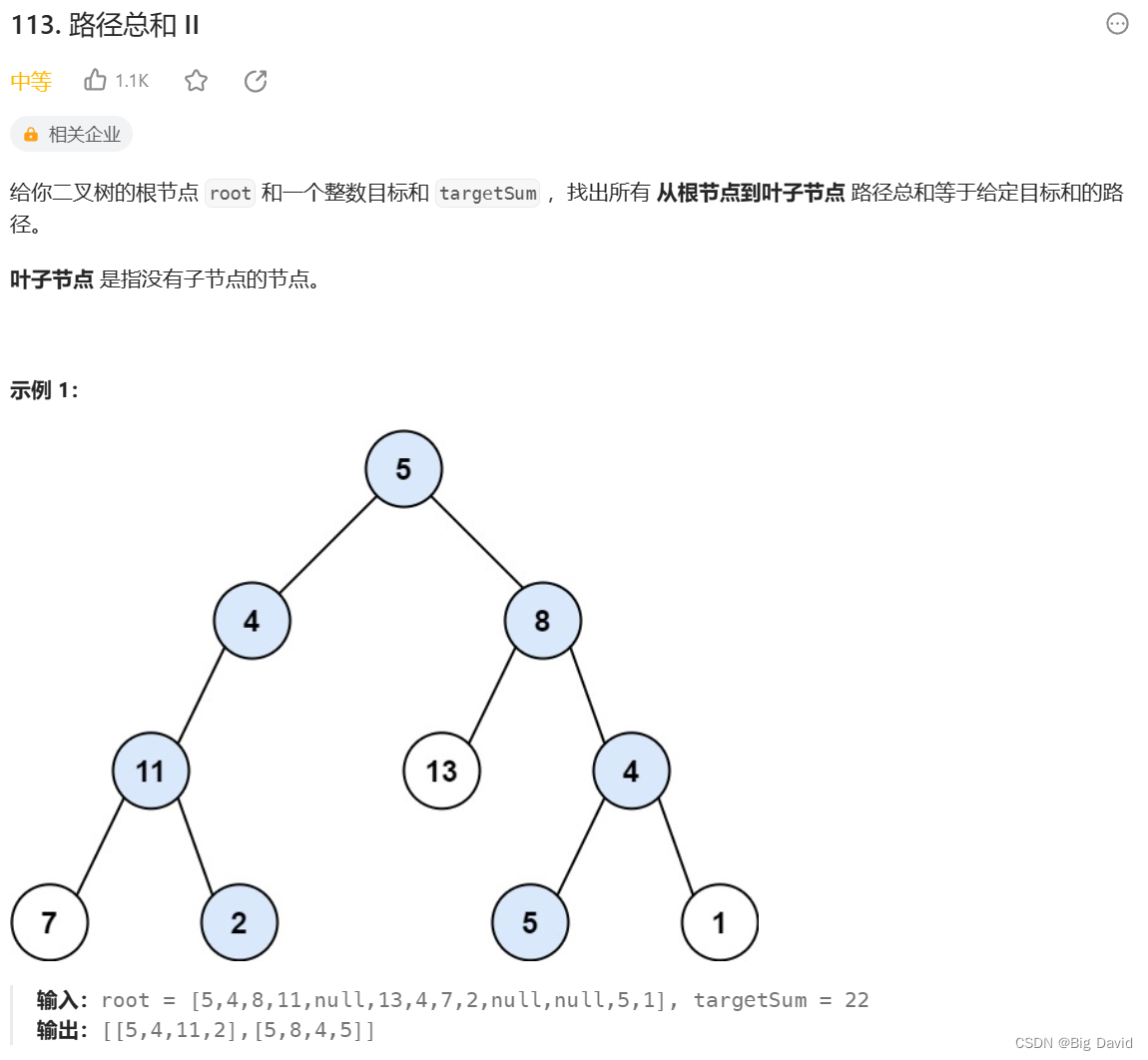
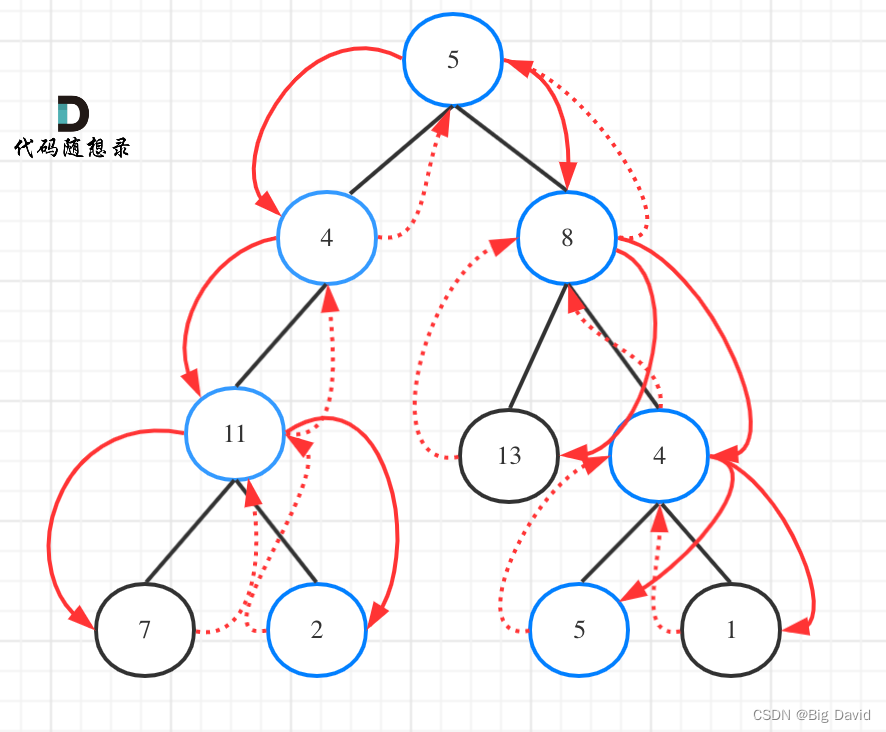
思路:
路径总和ii要遍历整个树,找到所有路径,所以递归函数不要返回值!
class Solution {
public:vector<vector<int>> result;vector<int> path;// 递归函数不需要返回值,因为我们要遍历整个树void traversal(TreeNode* node, int count) {if (node->left == NULL && node->right == NULL && count == 0) {result.push_back(path);return;}if (node->left == NULL && node->right == NULL) return;// 遇到叶子节点而没有找到合适的边,直接返回if (node->left) {// 左 (空节点不遍历)path.push_back(node->left->val);count -= node->left->val;traversal(node->left, count);// 递归count += node->left->val;// 回溯path.pop_back();// 回溯}if (node->right) {// 右 (空节点不遍历)path.push_back(node->right->val);count -= node->right->val;traversal(node->right, count);// 递归count += node->right->val;// 回溯path.pop_back();// 回溯}return;}vector<vector<int>> pathSum(TreeNode* root, int targetSum) {result.clear();path.clear();if (root == NULL) return result;path.push_back(root->val);// 把根节点放进路径traversal(root, targetSum - root->val);return result;}
};
3 从中序与后序遍历序列构造二叉树
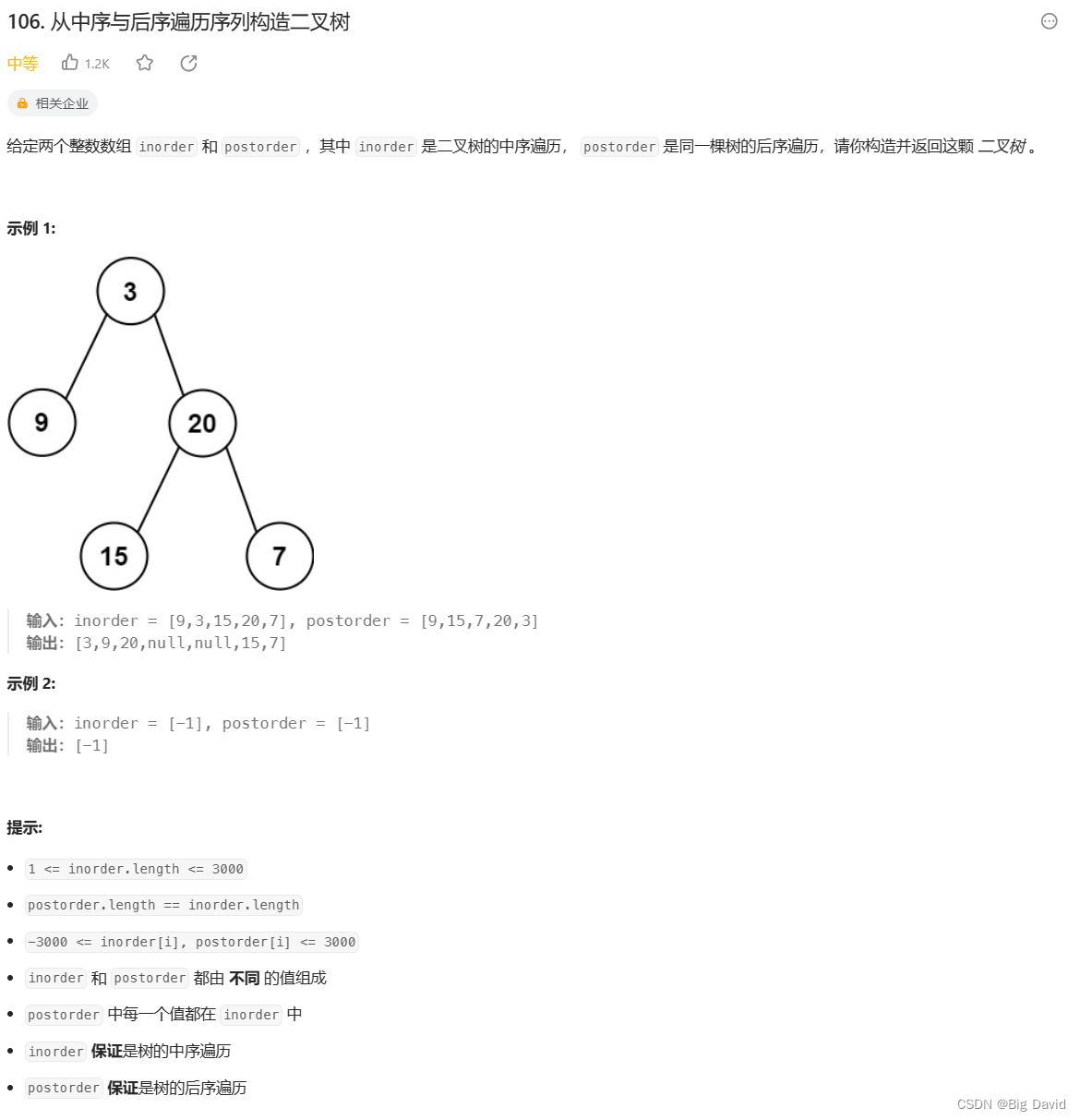
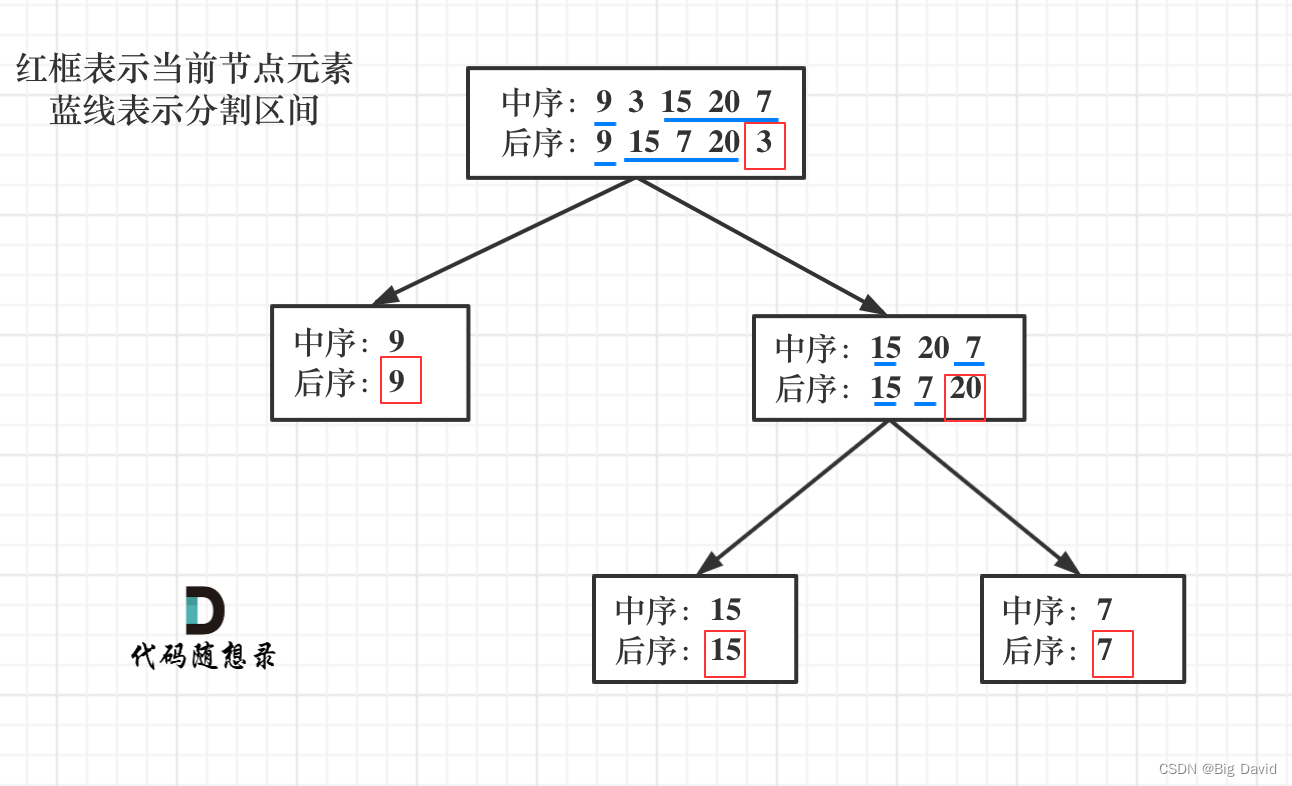
思路:
- 后序数组为0,空节点
- 后序数组最后一个元素为节点元素
- 寻找中序数组位置作为切割点
- 切中序数组
- 切后序数组
- 递归处理左右区间
C++:
class Solution {
public:TreeNode* traversal(vector<int>& inorder, vector<int>& postorder) {if (postorder.size() == 0) return NULL;// 后序遍历数组最后一个元素,就是当前的中间节点int rootValue = postorder[postorder.size() - 1];TreeNode* root = new TreeNode(rootValue);// 叶子节点if (postorder.size() == 1) return root;// 找到中序遍历的切割点int index;for (index = 0; index < inorder.size(); index++){if (inorder[index] == rootValue) break;}// 切割中序数组vector<int> leftInorder(inorder.begin(), inorder.begin() + index);vector<int> rightInorder(inorder.begin() + index + 1, inorder.end());postorder.resize(postorder.size() - 1);// 切割后序数组vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());root->left = traversal(leftInorder, leftPostorder);root->right = traversal(rightInorder, rightPostorder);return root;}TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {if (inorder.size() == 0 || postorder.size() == 0) return NULL;return traversal(inorder, postorder);}
};
4 从前序与中序遍历序列构造二叉树
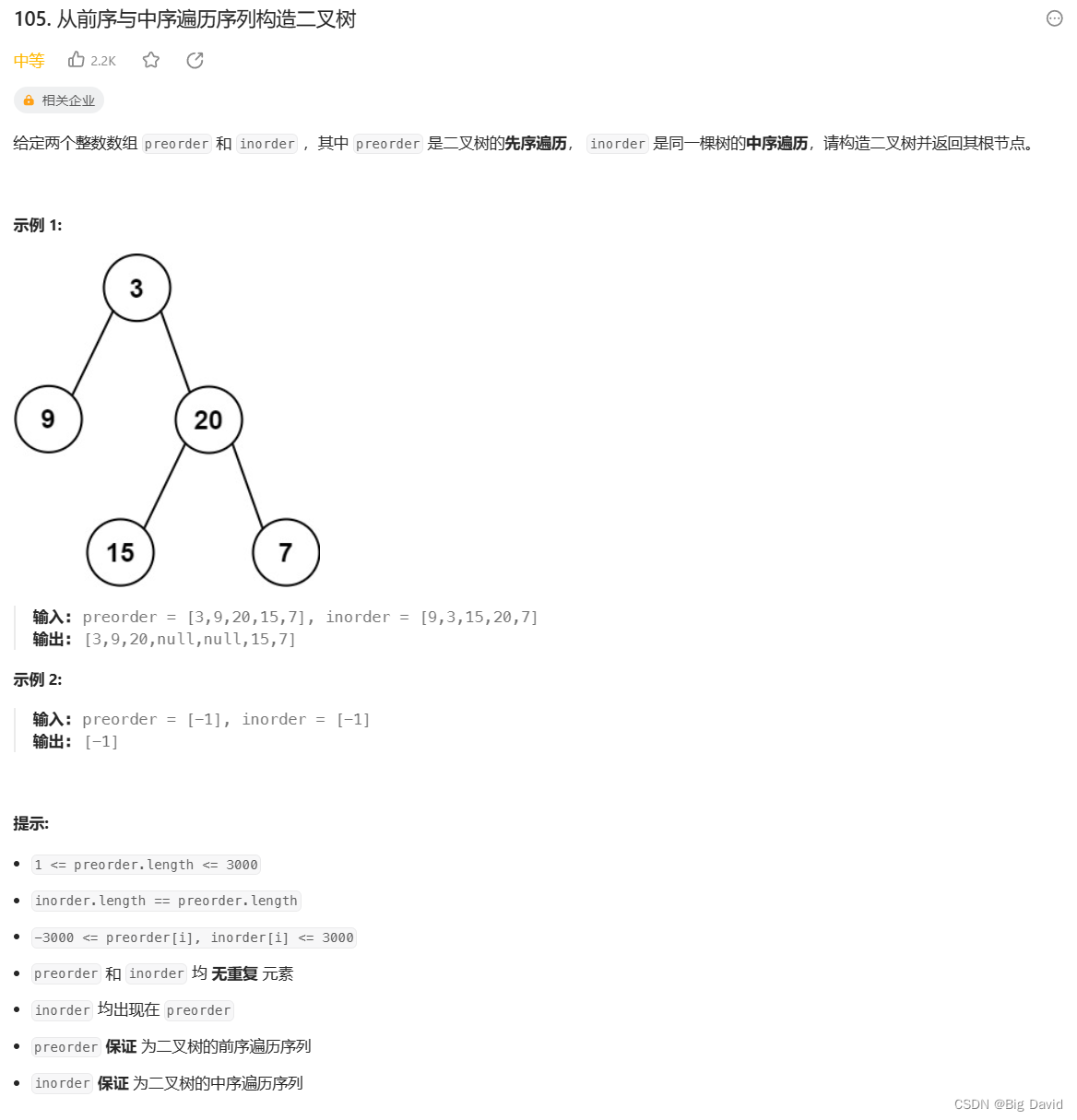
思路:
- 前序数组为0,空节点
- 前序数组第一个元素为节点元素
- 寻找中序数组位置作为切割点
- 切中序数组
- 切前序数组
- 递归处理左右区间
C++:
class Solution {
public:TreeNode* traversal(vector<int>& preorder, vector<int>& inorder) {// 前序数组为0,空节点if (preorder.size() == 0) return NULL;// 前序数组第一个元素为节点元素int rootValue = preorder[0];TreeNode* root = new TreeNode(rootValue);if (preorder.size() == 1) return root;// 寻找中序数组位置作为切割点int index;for (index = 0; index < inorder.size(); index++) {if (inorder[index] == rootValue) break;}// 切中序数组vector<int> leftInorder(inorder.begin(), inorder.begin() + index);vector<int> rightInorder(inorder.begin() + index + 1, inorder.end());// 切前序数组preorder.erase(preorder.begin());vector<int> leftPreorder(preorder.begin(), preorder.begin() + leftInorder.size());vector<int> rightPreorder(preorder.begin() + leftPreorder.size(), preorder.end());// 递归处理左右区间root->left = traversal(leftPreorder, leftInorder);root->right = traversal(rightPreorder, rightInorder);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {if (preorder.size() == 0 || inorder.size() == 0) return NULL;return traversal(preorder, inorder);}
};
鼓励坚持十六天的自己😀😀😀
相关文章:

代码随想录刷题题Day15
刷题的第十五天,希望自己能够不断坚持下去,迎来蜕变。😀😀😀 刷题语言:C Day15 任务 ● 513.找树左下角的值 ● 112. 路径总和 113.路径总和ii ● 106.从中序与后序遍历序列构造二叉树 105.从前序与中序遍历…...
软件设计师——信息安全(一)
📑前言 本文主要是【信息安全】——软件设计师——信息安全的文章,如果有什么需要改进的地方还请大佬指出⛺️ 🎬作者简介:大家好,我是听风与他🥇 ☁️博客首页:CSDN主页听风与他 🌄…...

git必须掌握:git远程变动怎么解决
如何已经指定了选择分支 那下面的分支名称可以省略 如果远程分支存在变动,通常 git 推送的流程如下: 首先,使用 git fetch 命令从远程仓库获取最新的分支信息和变动。 git fetch然后,可以使用 git merge 或者 git rebase 命令进…...

Python里的时间模块
time 模块 时间表示方式 时间戳 timestamp:表示的是从 1970 年1月1日 00:00:00 开始按秒计算的偏移量UTC(Coordinated Universal Time, 世界协调时)亦即格林威治天文时间,世界标准时间。在中国为 UTC+8 DST(Daylight Saving Time) 即夏令时;结构化时间(struct_time): …...
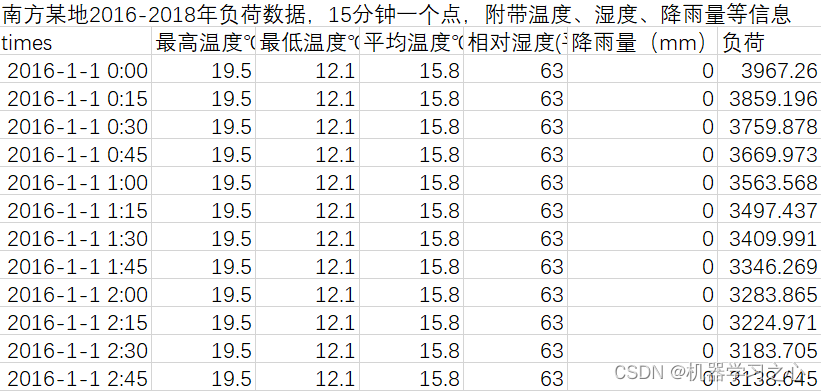
SCI一区级 | Matlab实现GWO-CNN-GRU-selfAttention多变量多步时间序列预测
SCI一区级 | Matlab实现GWO-CNN-GRU-selfAttention多变量多步时间序列预测 目录 SCI一区级 | Matlab实现GWO-CNN-GRU-selfAttention多变量多步时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 1.Matlab实现GWO-CNN-GRU-selfAttention灰狼算法优化卷积门控循环…...

C#学习相关系列之自定义遍历器
在C#中,自定义遍历器需要实现IEnumerable接口和IEnumerator接口。其中,IEnumerable接口包含一个GetEnumerator方法,该方法返回一个IEnumerator接口的实例,而IEnumerator接口包含Current、MoveNext和Reset方法。 IEnumerable&#…...
WPS没保存关闭了怎么恢复数据?3个方法,完成数据恢复!
“我今天在使用WPS时,突然有点急事出去了一趟,但是我忘记保存文档了,回来之后发现电脑自动关机了,我的文档也没了!这可怎么办呢?有什么办法可以找回这些数据吗?” 在快节奏的工作中,…...
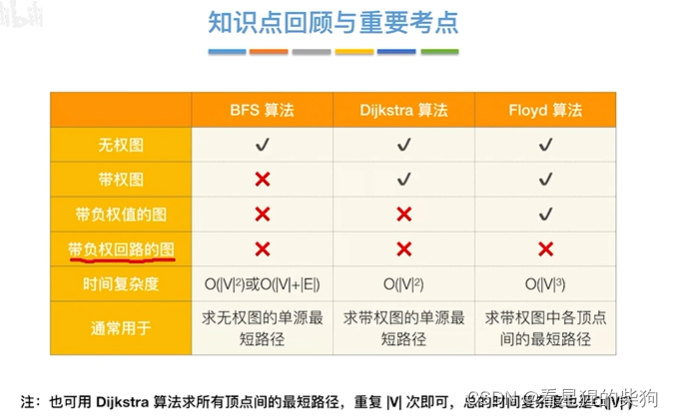
数据结构和算法-最小生成树(prim和krusakal)和最短路径问题(BFS和dijkastra和floyd)
文章目录 最小生成树总览生成树广度优先生成树深度优先生成树最小生成树Prim算法Kruskal算法Prim vs KrusakalPrim的实现Kruskal的实现 小结 最短路径问题单源最短路径问题BFS求无权图的单源最短路径小结Dijkastra算法算法时间复杂度不适用情况 每一对顶点的最短路径问题Floyd算…...
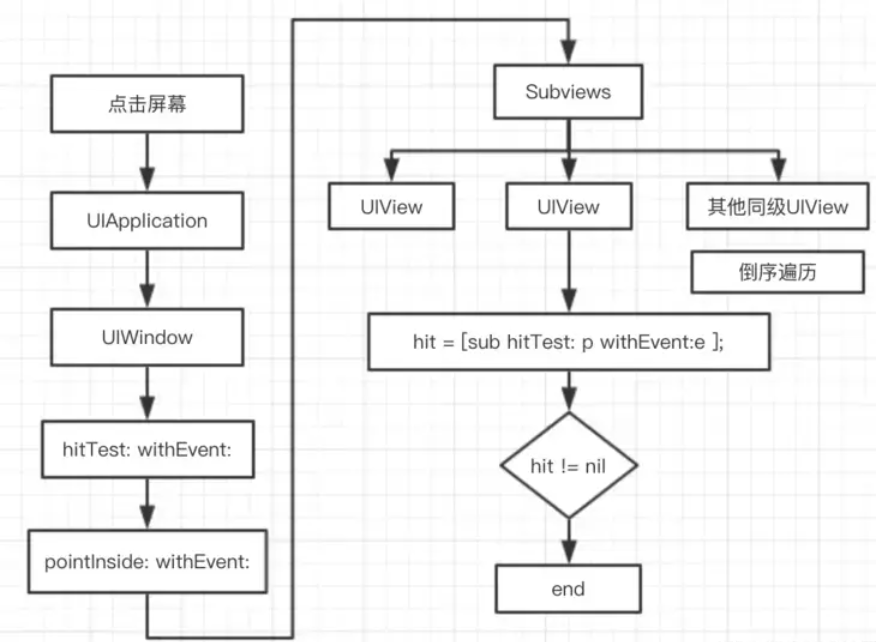
响应者链概述
响应者链 iOS事件的3大类型 Touch Events(触摸事件)Motion Events(运动事件,比如重力感应和摇一摇等)Remote Events(远程事件,比如用耳机上得按键来控制手机) 触摸事件 处理触摸事件的两个步骤 寻找事件的最佳响应者事件的响应在响应链中的传递 寻…...
ShenYu网关Http服务探活解析
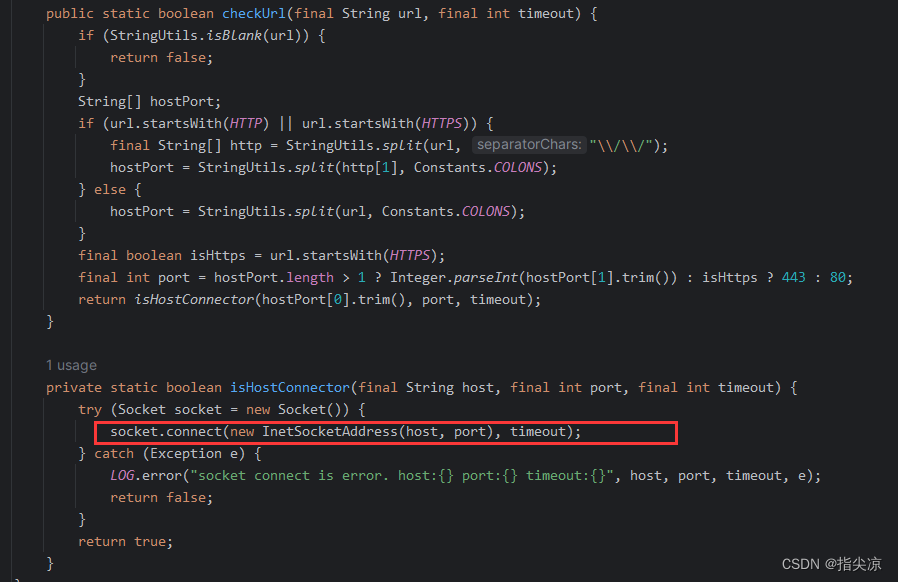
文章目录 网关端服务探活admin端服务探活 Shenyu HTTP服务探活是一种用于检测HTTP服务是否正常运行的机制。它通过建立Socket连接来判断服务是否可用。当服务不可用时,将服务从可用列表中移除。 网关端服务探活 以divide插件为例,看下divide插件是如何获…...
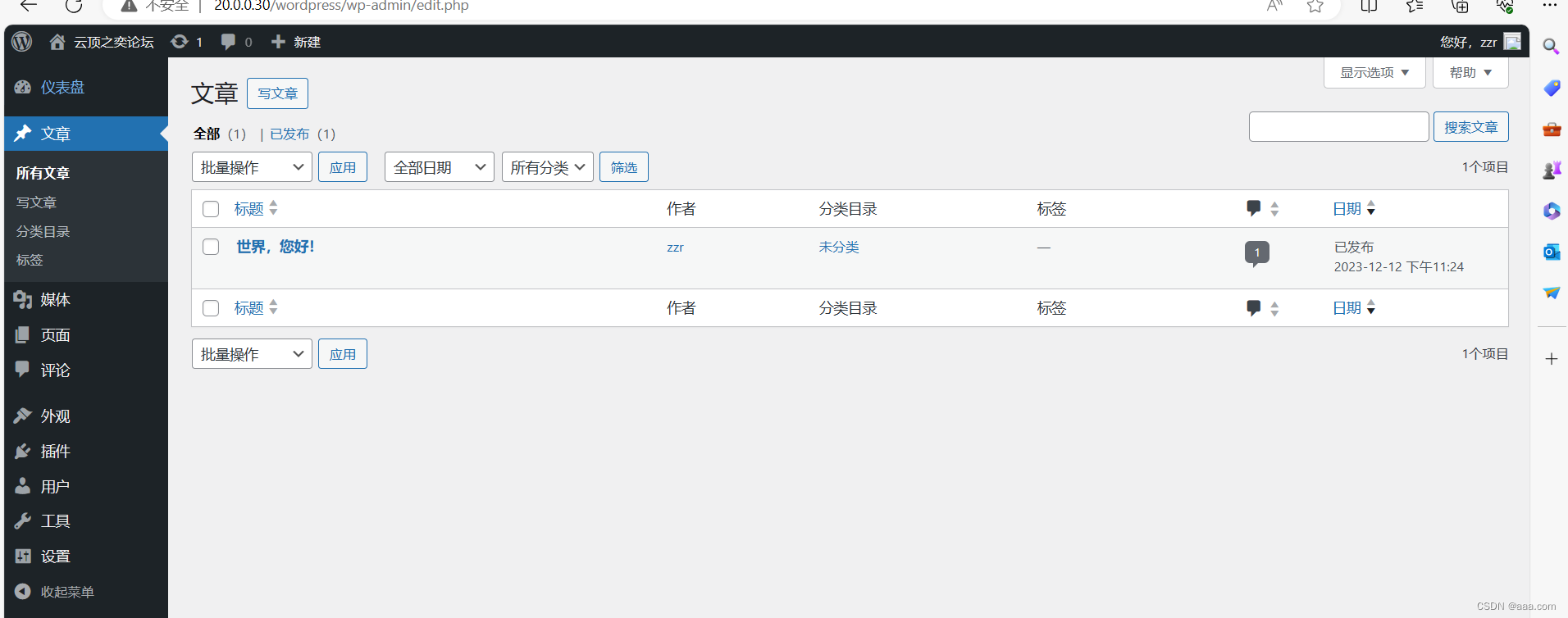
基于dockerfile搭建LNMP
组件自定义IP所需组件nginx172.111.0.10nginxwordpressmysql172.111.0.20mysql-5.7.20php172.111.0.30php LNMP介绍 L:Linux平台,操作系统,另外桑组件的运行平台 N:nginx 提供前端页面 M:MySQL,开源关系的…...
基于VGG-16+Android+Python的智能车辆驾驶行为分析—深度学习算法应用(含全部工程源码)+数据集+模型(三)
目录 前言总体设计系统整体结构图系统流程图 运行环境模块实现1. 数据预处理2. 模型构建3. 模型训练及保存1)模型训练2)模型保存 4. 模型生成1)模型导入及调用2)相关代码(1)布局文件(2ÿ…...
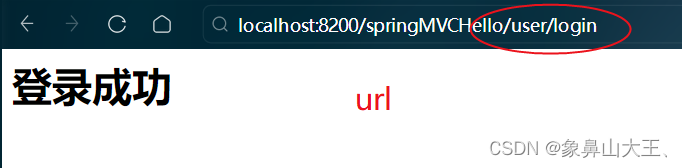
springMVC-@RequestMapping
基本介绍 RequestMapping注解可以指定控制器/处理器的某个方法的请求的url, 示例 (结合springMVC基本原理理解) Controller public class UserHandler {RequestMapping(value "/login")public String login() {System.out.println("登…...

智能优化算法应用:基于树种算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于树种算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于树种算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.树种算法4.实验参数设定5.算法结果6.参考文献7.MA…...

web前端项目-影视网站开发
影视网站 本项目主要使用到了 HTML;CSS;JavaScript脚本技术;AJAX无刷新技术;jQuery等技术实现了动态影视网页 运行效果: 一:index.html <!DOCTYPE> <html lang"en"> <head>…...
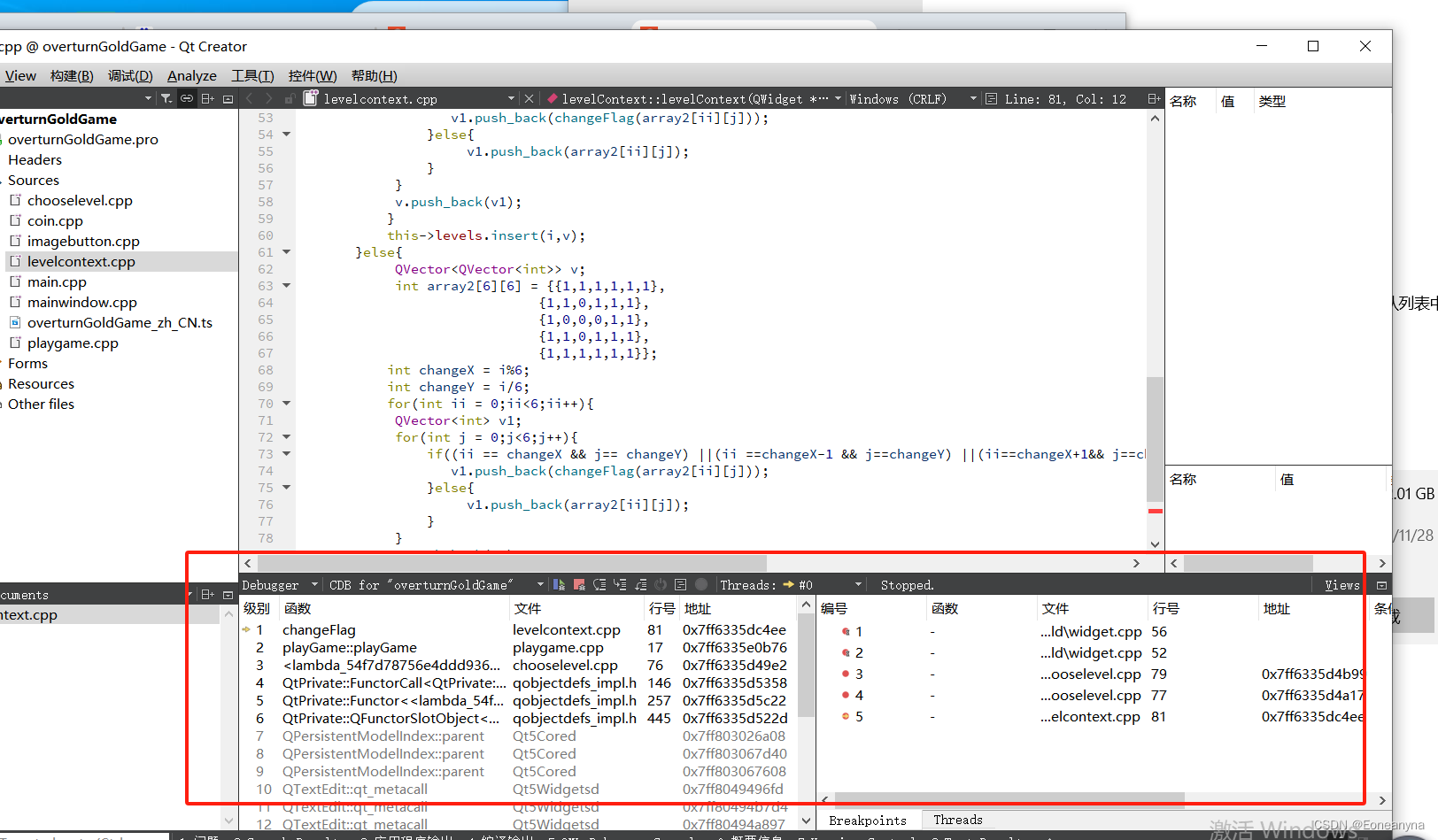
QT:Unable to create a debugging engine.
debug跑不了: 报错:Unable to create a debugging engine. 参考: https://blog.csdn.net/u010906468/article/details/104716198 先检查是否安装了DEBUG插件 工具-》》选项 查看插件,如果没有的话,需要重新安装qt时…...

如何理解Rust语言中的“impl”关键字
在Rust编程语言中,impl是一个关键字,用于为类型实现方法和特性(traits)。impl关键字后面可以跟一个类型或者特性名称,然后在大括号中定义该类型或特性的具体实现。 当我们使用impl关键字为一个类型实现方法时…...

C++实现简单的猜数字小游戏
猜数字 小游戏介绍:猜数字游戏是令游戏机随机产生一个100以内的正整数,用户输入一个数对其进行猜测,需要你编写程序自动对其与随机产生的被猜数进行比较,并提示大了,还是小了,相等表示猜到了。如果猜到&…...

人工智能导论复习资料
题型 1、简答题(5题) 2、设计题 3、综合题 4、论述题(10分) 考点 第一章 1、人工智能的定义、发展; 2、人工智能的学派、认知观及其间的关系; 3、人工智能要素及系统分类; 4、人工智能的研究、…...

Sentinel使用详解
组件简介 Sentinel是阿里开源的一套用于服务容错的综合性解决方案。它以流量为切入点,从流量控制、熔断降级、系统负载保护等多个维度来保护服务的稳定性。Sentinel承接了阿里巴巴近10年的双十一大促流量的核心场景,例如秒杀、消息削峰填谷、集群流量控…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...