代码随想录27期|Python|Day16|二叉树|104.二叉树的最大深度|111.二叉树的最小深度|222.完全二叉树的节点个数
二叉树专题,重点掌握后续的递归和中间节点的处理。
104. 二叉树的最大深度 - 力扣(LeetCode)
本题在前一章已经解决了层序遍历的解法,现在来聊一下递归法。
首先需要明确两个概念:深度和高度。(注意,起始位置的值都是1)
深度:从root开始,到当前位置所在节点的层数;
高度:从底层叶子节点开始,到当前所在节点的层数。

再来说一下选择什么顺序来遍历。
前序:从root出发,直接找的是深度;
后序:从叶子节点出发,返回给root节点高度。
也就是说,不管选择哪一种,中间节点都是单独处理的。
后序遍历
按照递归的书写三部曲,可以写出后序遍历的方法。
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):def maxDepth(self, root):""":type root: TreeNode:rtype: int"""# 后序遍历(Version 1)# step1 确定返回值类型:TreeNode# step2 确定终止条件:当前节点是空if not root:return 0else:# step3 单层处理:按照“左右中”的顺序,先遍历左节点高度,再遍历右节点高度,汇总到中间节点取较大值,再加1(因为当前中间节点也算作一层)left_height = self.maxDepth(root.left)right_height = self.maxDepth(root.right)return max(left_height, right_height) + 1# 精简递归(Version 2)return 0 if not root else max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1前序遍历
要麻烦很多,还涉及到回溯算法,十分甚至九分的不推荐。
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):def maxDepth(self, root):""":type root: TreeNode:rtype: int"""# 递归(前序遍历)res = 0if not root:return 0self.getdepth(root, 1)return resdef getdepth(self, node, depth):res = max(depth, res)if node.left == None and node.right == None:returnif node.left:depth += 1self.getdepth(node.left, depth)depth -= 1 # 回溯算法if node.right:depth += 1self.getdepth(node.right, depth)depth -= 1return559. N 叉树的最大深度 - 力扣(LeetCode)
和上面相似的一道题,只用了递归+左右中的后序遍历。
只需要用for遍历所有孩子节点(其实就是上面分别判断左节点和右节点的推广)。
"""
# Definition for a Node.
class Node(object):def __init__(self, val=None, children=None):self.val = valself.children = children
"""class Solution(object):def maxDepth(self, root):""":type root: Node:rtype: int"""if not root:return 0max_depth = 1 # 在排除顶部节点是空的时候初始化最大值是1# 遍历所有的孩子节点for child in root.children:# 注意在每次比较的时候+ 1,表示计算上了中间节点max_depth = max(self.maxDepth(child) + 1, max_depth)return max_depth111. 二叉树的最小深度 - 力扣(LeetCode)
本题需要注意的是和上面求解最大值需要遍历到底不一样,本题需要遍历到第一个叶子节点,也就是左右子树都没有的第一个节点。
依然使用后序遍历。
递归法
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):def minDepth(self, root):""":type root: TreeNode:rtype: int"""# 递归法if not root:return 0else:# 左left_height = self.minDepth(root.left)# 右right_height = self.minDepth(root.right)# 中if root.left and root.right == None: # 左子树存在,右子树不存在return left_height + 1if root.right and root.left == None: # 右子树存在左子树不存在return right_height + 1# 遇到叶子节点返回到中间节点的最小值return min(left_height, right_height) + 1精简递归
把求解左右高度的简化到中间处理的返回值处。
# 左left_height = self.minDepth(root.left)# 右right_height = self.minDepth(root.right)222. 完全二叉树的节点个数 - 力扣(LeetCode)
递归(后序遍历)
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):def countNodes(self, root):""":type root: TreeNode:rtype: int"""# 当作普通二叉树if not root:return 0# 左left_num = self.countNodes(root.left)# 右right_num = self.countNodes(root.right)# 中return left_num + right_num + 1# 精简版if not root:return 0return self.countNodes(root.left) + self.countNodes(root.right) + 1利用完全二叉树递归
题干当中还特别说明了是完全二叉树,所以我们可以使用完全二叉树在左右外侧深度相等的时候是满二叉树的性质来统计。
简单概括就是:如果这一层的左子树的左深度和右子树的右深度相等,那么就可以判断现在这是满二叉树。
利用这个性质,我们就很容易可以判断满足满二叉树的条件。
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):def countNodes(self, root):""":type root: TreeNode:rtype: int"""# 利用完全二叉树if not root:return 0# 判断是满二叉树直接输出leftnode = root.leftrightnode = root.rightleft_depth, right_depth = 0, 0while leftnode:leftnode = leftnode.leftleft_depth += 1while rightnode:rightnode = rightnode.rightright_depth += 1if left_depth == right_depth:return (2 << left_depth) - 1 # 2 << 1 = 2 ^ 2# 普通二叉树正常递归输出return self.countNodes(root.left) + self.countNodes(root.right) + 1第16天完结🎉
相关文章:

代码随想录27期|Python|Day16|二叉树|104.二叉树的最大深度|111.二叉树的最小深度|222.完全二叉树的节点个数
二叉树专题,重点掌握后续的递归和中间节点的处理。 104. 二叉树的最大深度 - 力扣(LeetCode) 本题在前一章已经解决了层序遍历的解法,现在来聊一下递归法。 首先需要明确两个概念:深度和高度。(注意&…...

༺༽༾ཊ—设计-简介-模式—ཏ༿༼༻
我对设计模式的理解就是一种可复用的且面向对象的设计工具,它与代码无关,我们可以利用设计模式设计出高内聚、低耦合的应用程序,并且最大程度实现程序的复用,以应对复杂的需求变化。 程序的可复用性就是用已存在的程序模块进行更新…...

Matplotlib快速入门,Python通用的绘图工具库上手
Matplotlib是一个用于Python编程语言的综合性绘图库。 它可以生成各种类型的图表,包括折线图、条形图、散点图、直方图、饼图等。Matplotlib支持多种数据格式,包括NumPy数组、Pandas DataFrame和CSV文件。它还可以从URL读取数据。 Matplotlib可以在交互…...
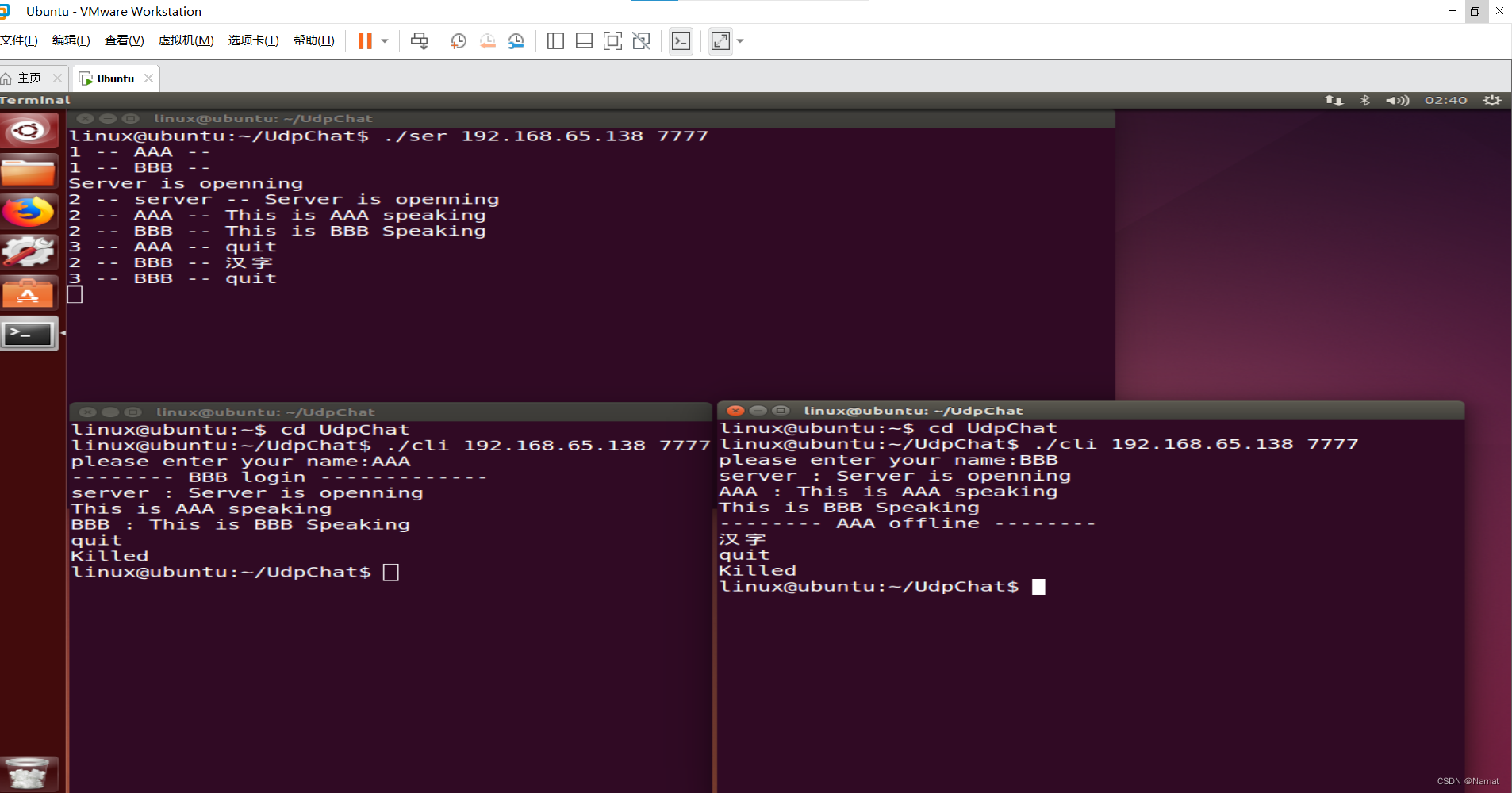
Linux 基本语句_16_Udp网络聊天室
代码: 服务端代码: #include <stdio.h> #include <arpa/inet.h> #include <sys/types.h> #include <sys/socket.h> #include <netinet/in.h> #include <stdlib.h> #include <unistd.h> #include <string…...
使用ffmpeg命令进行视频格式转换
1 ffmpeg介绍 FFmpeg 是一个非常强大和灵活的开源工具集,用于处理音频和视频文件。它提供了一系列的工具和库,可以用于录制、转换、流式传输和播放音频和视频。 FFmpeg 主要特点如下: 格式支持广泛:FFmpeg 支持几乎所有的音频和视…...
)
Mac安装Adobe AE/pr/LR/ai/ps/au/dw/id 2024/2023报错问题解决(常见错误:已损坏/2700/146/130/127)
1.打开允许“允许任何来源” 如何打开允许任何来源?在 Finder 菜单栏选择 【前往】 – 【实用工具 】,找到【终端】程序,双击打开,在终端窗口中输入:sudo spctl --master-disable 输入代码后,按【return …...

Python三级 每周练习题31
如果你感觉有收获,欢迎给我微信扫打赏码 ———— 以激励我输出更多优质内容 练习一: 作业1:编写程序,在下面的字典中找出身高137的同学并输出姓名,如果没找到, 输出没有 a{‘小赵’:136,‘小钱’:141,‘小孙’:146,‘小李’:13…...
【DataSophon】大数据服务组件之Flink升级
🦄 个人主页——🎐开着拖拉机回家_Linux,大数据运维-CSDN博客 🎐✨🍁 🪁🍁🪁🍁🪁🍁🪁🍁 🪁🍁🪁&am…...

Android笔记(十八):面向Compose组件结合Retrofit2和Rxjava3实现网络访问
一、Retrofit2 Square公司推出的Retrofit2库(https://square.github.io/retrofit/),改变了网络访问的方式。它实现了网络请求的封装。Retrofit库采用回调处理方式,使得通过接口提交请求和相应的参数的配置,就可以获得…...

mybatis中oracle的sql没走索引导致特别慢(未加jdbcType的)
如果直接跑sql是能走索引很快,在mybatis中不能,可能就是jdbcType的原因。 比如,我有一个属性A,在表里面是VARCHAR2类型,但是在mybatis中的sql是#{a},缺少jdbcTypeJdbcType.VARCHAR,就会导致myba…...
QT自带打包问题:无法定位程序输入点?metaobject@qsound
文章目录 无法定位程序输入点?metaobjectqsound……检查系统环境变量的配置:打包无须安装qt的文件 无法定位程序输入点?metaobjectqsound…… 在执行release打包程序后,相应的release文件夹下的exe文件,无法打开 如有错误欢迎指出 检查系…...

7.3 lambda函数
一、语法 1.基础语法 [capture](paramLists) mutable ->retunType{statement} capture。捕获列表,用于捕获前文的变量供lambda函数中使用,可省略。(paramLists)。参数列表,可省略。mutable。lambda表达式默认具有常量性,可以…...
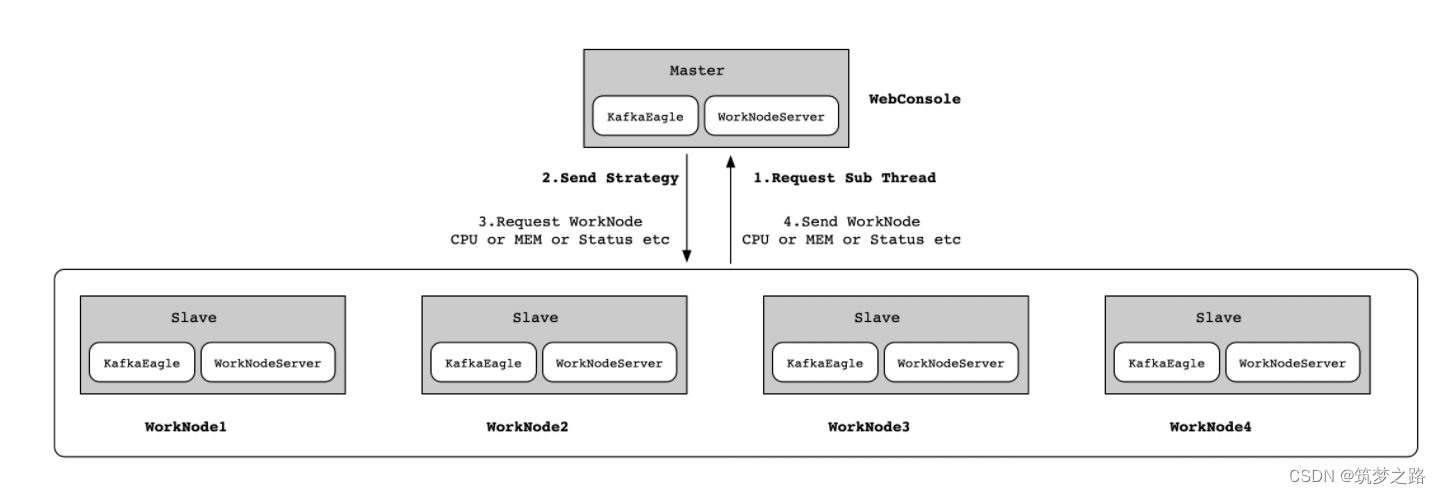
dcoker-compose一键部署EFAK —— 筑梦之路
简介 EFAK(Eagle For Apache Kafka,以前称为 Kafka Eagle)是一款由国内公司开源的Kafka集群监控系统,可以用来监视kafka集群的broker状态、Topic信息、IO、内存、consumer线程、偏移量等信息,并进行可视化图表展示。独…...

音视频:Ubuntu下安装 FFmpeg 5.0.X
1.安装相关依赖 首可选一: sudo apt-get update sudo apt-get install build-essential autoconf automake libtool pkg-config \libavcodec-dev libavformat-dev libavutil-dev \libswscale-dev libresample-dev libavdevice-dev \libopus-dev libvpx-dev libx2…...
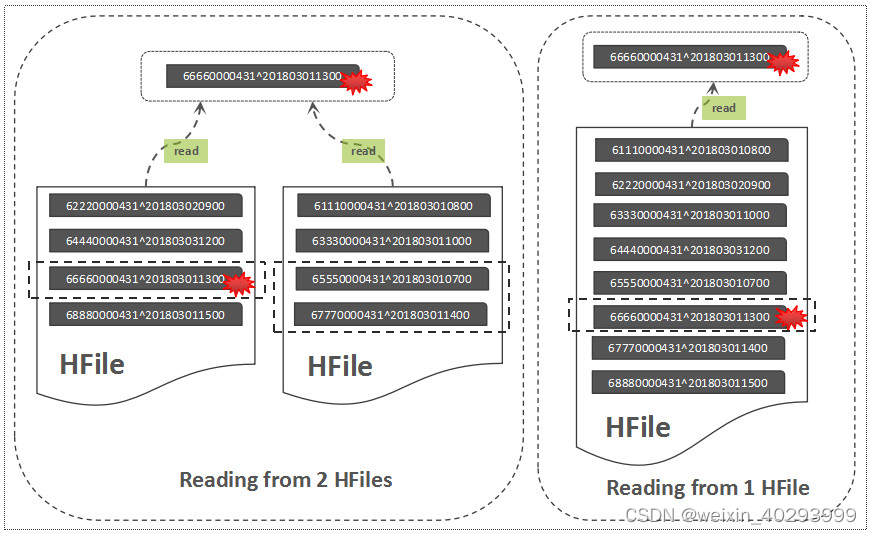
【LSM tree 】Log-structured merge-tree 一种分层、有序、面向磁盘的数据结构
文章目录 前言基本原理读写流程写流程读流程 写放大、读放大和空间放大优化 前言 LSM Tree 全称是Log-structured merge-tree, 是一种分层,有序,面向磁盘的数据结构。其核心原理是磁盘批量顺序写比随机写性能高很多,可以通过围绕这一原理进行…...
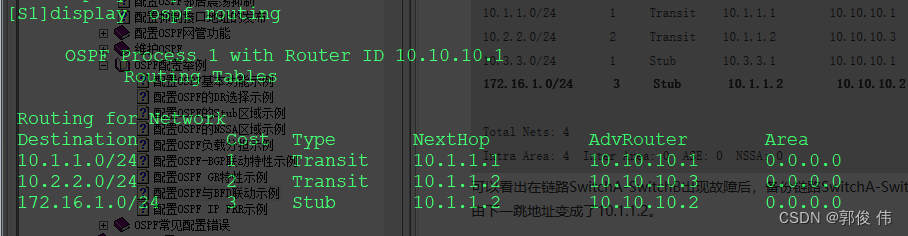
配置OSPF与BFD联动示例
定义 双向转发检测BFD(Bidirectional Forwarding Detection)是一种用于检测转发引擎之间通信故障的检测机制。 BFD对两个系统间的、同一路径上的同一种数据协议的连通性进行检测,这条路径可以是物理链路或逻辑链路,包括隧道。 …...

01到底应该怎么理解“平均负载”
1、如何了解系统的负载情况? 每次发现系统变慢时, 我们通常做的第⼀件事, 就是执⾏top或者uptime命令, 来了解系统的负载情况。 ⽐如像下⾯这样, 我在命令⾏⾥输⼊了uptime命令, 系统也随即给出了结果。 …...

jmeter,动态参数之随机数、随机日期
通过函数助手,执行以下配置: 执行后的结果树: 数据库中也成功添加了数据,对应字段是随机值:...

uniApp常见知识点-问题答案
1、uniApp中如何进行页面跳转? 答案:可以使用 uni.navigateTo、uni.redirectTo 和 uni.reLaunch 等方法进行页面跳转。其中,uni.navigateTo可以实现页面的普通跳转, uni.redirectTo可以实现页面的重定向跳转, uni.reL…...

云原生基础入门概念
文章目录 发现宝藏云原生的概念云原生的关键技术为何选择云原生?云原生的实际应用好书推荐 发现宝藏 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。【宝藏入口】。 云原生的概念 当谈及现…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

jdbc查询mysql数据库时,出现id顺序错误的情况
我在repository中的查询语句如下所示,即传入一个List<intager>的数据,返回这些id的问题列表。但是由于数据库查询时ID列表的顺序与预期不一致,会导致返回的id是从小到大排列的,但我不希望这样。 Query("SELECT NEW com…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...
