安全算法(二):共享密钥加密、公开密钥加密、混合加密和迪菲-赫尔曼密钥交换
安全算法(二):共享密钥加密、公开密钥加密、混合加密和迪菲-赫尔曼密钥交换
本章介绍了共享密钥加密、公开密钥加密,和两种加密方法混合使用的混合加密方法;最后介绍了迪菲-赫尔曼密钥交换。
加密数据的方法可以分为两种:加密和解密都使用相同密钥的“共享密钥加密”和分别使用不同密钥的“公开密钥加密”。以下将分别介绍。
共享密钥加密
共享密钥加密是加密和解密都使用相同密钥的一种加密方式。由于使用的密钥相同,所以这种算法也被称为**“对称加密”**。

假设 A 准备通过互联网向 B 发送数据。由于有被窃听的风险,所以需要把想要保密的数据加密后再发送。A使用密钥加密数据后再发送给B。B 收到密文后,使用相同的密钥对其进行解密。这样,B 就取得了原本的数据。只要是加密好的数据,就算被第三者恶意窃听也无须担心。
*实现共享密钥加密的算法有凯撒密码、AES、DES、动态口令等,其中 AES 的应用最为广泛。
AES: Advanced Encryption Standard
DES: Data Encryption Standard
共享密钥加密中存在的问题

B收到A发送密文时,密文可能已经被窃听。假设A和B无法直接沟通,B不知道加密时使用的什么密钥。A 需要通过某种手段将密钥交给 B。和密文一样,A 又在互联网上向 B 发送了密钥。B 使用收到的密钥对密文进行解密。但是,该密钥也有可能会被 X 窃听。这样一来, X 也可以使用密钥对密文进行解密了。

为了解决这个问题,需要找到可以把密钥安全送出的方法,即“密钥分配问题”。要想解决这个问题,可以使用**“密钥交换协议”和“公开密钥加密”**两种方法。
公开密钥加密
公开密钥加密是加密和解密使用不同密钥的一种加密方法。由于使用的密钥不同,所以这种算法也被称为“非对称加密”。加密用的密钥叫作**“公开密钥”**,解密用的叫作“私有密钥”。

假设 A 准备通过互联网向 B 发送数据。首先,需要由接收方 B 来生成公开密钥 P 和私有密钥 S 。然后把公开密钥发送给A。A 使用 B 发来的公开密钥加密数据。A 将密文发送给 B,B 再使用私有密钥对密文进行解密。这样,B 就得到了原本的数据。

*实现公开密钥加密的算法有RAS 算法、椭圆曲线加密算法等,其中使用最为广泛的是 RSA 算法。
与共享密钥加密不同的是, 公开密钥加密不会出现密钥分配问题。
公开密钥和密文都是通过互联网传输的,因此可能会被 X 窃听。但是,使用公开密钥无法解密密文,因此 X 也无法得到原本的数据。

此外,在和多人传输数据时,使用公开密钥加密十分方便。

公开密钥是不怕被人知道的,所以 B 可以把公开密钥发布在网上。与此相反,私有密钥不能被人知道,必须严密保管。假设有许多人都想向 B 发送数据。想发送数据的人首先在网上取得 B 发布的公开密钥。然后用它加密要发送的数据。最后把密文发给 B。
B 用私有密钥对收到的密文进行解密,取得原本的数据。这种情况就不需要为每个发送对象都准备相对应的密钥了。需要保密的私有密钥仅由接收方保管,所以安全性也更高。

公开密钥加密中存在的问题
“中间人攻击“

X 把公开密钥 PB 替换成自己的公开密钥 PX。A 使用公开密钥 PX 对数据加密。当A把想要给B的密文发送出去后,X接收了这个密文。这个密文由X 生成的公开密钥PX 加密而成,所以 X 可以用自己的私有密钥 SX 对密文进行解密。接下来,X 用 B 生成的公开密钥 PB 加密数据。X把密文发送给B,这个密文由B发出的公开密钥PB 加密而成,所以B可以用自己的私有密钥 SB 来解密。
从收到密文到解密密文都没发生任何问题,因此 B 也意识不到数据已经被窃听。
公开密钥的可靠性会出现问题,就是因为 A 无法判断收到的公开密钥是否来自 B。要想解决这个问题,就要用到之后会讲到的**“数字证书”**。
公开密钥加密还有一个问题,那就是加密和解密都比较耗时,所以这种方法不适用 于持续发送零碎数据的情况。要想解决这个问题,就要用到**“混合加密”**。
*考虑到加密所需的计算流程,算法必须满足如下条件。
① 可以使用某个数值对数据进行加密(计算)。
② 使用另一个数值对加密数据进行计算就可以让数据恢复原样。
③ 无法从一种密钥推算出另一种密钥。
混合加密
共享密钥加密存在无法安全传输密钥的密钥分配问题,公开密钥加密又存在加密解密速度较慢的问题。结合这两种方法以实现互补的一种加密方法就是混合加密。

在混合加密中,要用处理速度较快的共享密钥加密对数据进行加密。不过,加密时使用的密钥,则需要用没有密钥分配问题的公开密钥加密进行处理。

使用处理速度较快的共享密钥加密对数据进行加密。加密时所用的密钥在解密时也要用到,因此 A 需要把密钥发送给 B。将密钥通过公开密钥加密进行加密后,A 就可以将其安全地发送给 B 了。因此,作为接收方,B 需要事先生成公开密钥 P 和私有密钥 S 。然后,B 将公开密钥发送给 A。

A 使用收到的公开密钥,对共享密钥加密中需要使用的密钥进行加密,并将加密后的密钥法发送给B。B 使用私有密钥对密钥进行解密。

接下来,A 只要将使用这个密钥加密好的数据发送给 B 即可。加密数据时使用的是处理速度较快的共享密钥加密。
像这样,混合加密在安全性和处理速度上都有优势。能够为网络提供通信安全的 SSL 协议也应用了混合加密方法。SSL 是 Secure Sockets Layer(安全套接层)的简写,该协议经过版本升级后,现在已正式命名为 TLS(Transport Layer Security,传输层安全)。但是,SSL 这个名字在人们心中已经根深蒂固,因此该协议现在也常被称为 SSL 协议或者 SSL / TLS 协议。
迪菲-赫尔曼密钥交换
迪菲 - 赫尔曼(Diffie-Hellman)密钥交换是一种可以在通信双方之间安全交换密钥的方法。这种方法通过将双方共有的秘密数值隐藏在公开数值相关的运算中,来实现双方之间密钥的安全交换。

假设有一种方法可以合成两个密钥。使用这种方法来合成密钥 P 和密钥 S,就会得到由这两个密钥的成分所构成的密钥 P-S。这种方法有三个特征:
一、即使持有密钥 P 和合成的密钥 P-S, 也无法把密钥 S 单独取出来。即密钥之间可以合成,但不能分解。
二、不管是怎样合成而来的密钥,都可以把它作为新的元素,继续与别的密钥进行合成。即使用密钥 P 和密钥 P-S,还能合成出新的密钥 P-P-S。
三、密钥的合成结果与合成顺序无关,只与用了哪些密钥有关。如下图。

应用实例:

通过图示方法,A 和 B 都得到了密钥 P-SA-SB。这个密钥将作为 “加密密钥”和“解密密钥”来使用。

由于密钥无法被分解, 所以 X 无法取得私有密钥 SA 和 SB。在公开的密钥中,X无法用自己 窃听到的密钥合成出 P-SA-SB,因此这种交换方式是安全的。

以上用公式来表示这种密钥交换法。用 P、G 两个整数来表示一开始生成的公开密钥 P。其中 P 是一 个非常大的素数,而 G 是素数 P 所对应的生成元(或者“原根”)中的一个。
A 和 B 分别准备了各自的秘密数字 X 和 Y。X 和 Y 都必须小于 P-2。
A 和 B 分别计算“(G 的 秘密数字次方)mod P”。mod 运算就是取余运算 。“ G mod P”就是计算G 除以P 后的余数。此处的运算等同于概念意义上的“合成”
然后,A和B交换以上计算结果,并计算这个值的秘密数字次方,然后再mod P。最后会得到相同结果。

同理,窃听者X无法获得最终结果。
*根据素数 P、生成元 G 和“G^X mod P”求出 X 的问题就是“离散对数问题”,人们至今还未找到这个问题的解法,而迪菲 - 赫尔曼密钥交换正是利用了这个数学难题。
实际上,双方并没有交换密钥,而是生成了密钥。因此,该方法又被叫作**“迪菲 - 赫尔曼密钥协议”**。
参考资料:我的第一本算法书 (石田保辉 宮崎修一)
相关文章:

安全算法(二):共享密钥加密、公开密钥加密、混合加密和迪菲-赫尔曼密钥交换
安全算法(二):共享密钥加密、公开密钥加密、混合加密和迪菲-赫尔曼密钥交换 本章介绍了共享密钥加密、公开密钥加密,和两种加密方法混合使用的混合加密方法;最后介绍了迪菲-赫尔曼密钥交换。 加密数据的方法可以分为…...

MYSQL练题笔记-高级字符串函数 / 正则表达式 / 子句-简单3题
这个系列先写了三题,比较简单写在一起。 1.修复表中的名字相关的表和题目如下 看题目就知道是有关字符串函数的,于是在书里查询相关的函数,如下图,但是没有完全对口的函数,所以我还是去百度了。 然后发现结合上面的4个…...

vue扭蛋机抽奖游戏
简易扭蛋机demo 这是一个使用CSS3和JavaScript实现的扭蛋机抽奖游戏。该游戏的主要功能是通过点击按钮进行抽奖,抽奖过程中会显示滚动的小球,最终随机停止并显示一个中奖小球。 该游戏的抽奖过程如下: 当用户点击抽奖按钮时,首先检查当前是否正在进行抽奖任务或者当前有小…...

代码随想录27期|Python|Day16|二叉树|104.二叉树的最大深度|111.二叉树的最小深度|222.完全二叉树的节点个数
二叉树专题,重点掌握后续的递归和中间节点的处理。 104. 二叉树的最大深度 - 力扣(LeetCode) 本题在前一章已经解决了层序遍历的解法,现在来聊一下递归法。 首先需要明确两个概念:深度和高度。(注意&…...

༺༽༾ཊ—设计-简介-模式—ཏ༿༼༻
我对设计模式的理解就是一种可复用的且面向对象的设计工具,它与代码无关,我们可以利用设计模式设计出高内聚、低耦合的应用程序,并且最大程度实现程序的复用,以应对复杂的需求变化。 程序的可复用性就是用已存在的程序模块进行更新…...

Matplotlib快速入门,Python通用的绘图工具库上手
Matplotlib是一个用于Python编程语言的综合性绘图库。 它可以生成各种类型的图表,包括折线图、条形图、散点图、直方图、饼图等。Matplotlib支持多种数据格式,包括NumPy数组、Pandas DataFrame和CSV文件。它还可以从URL读取数据。 Matplotlib可以在交互…...
Linux 基本语句_16_Udp网络聊天室
代码: 服务端代码: #include <stdio.h> #include <arpa/inet.h> #include <sys/types.h> #include <sys/socket.h> #include <netinet/in.h> #include <stdlib.h> #include <unistd.h> #include <string…...
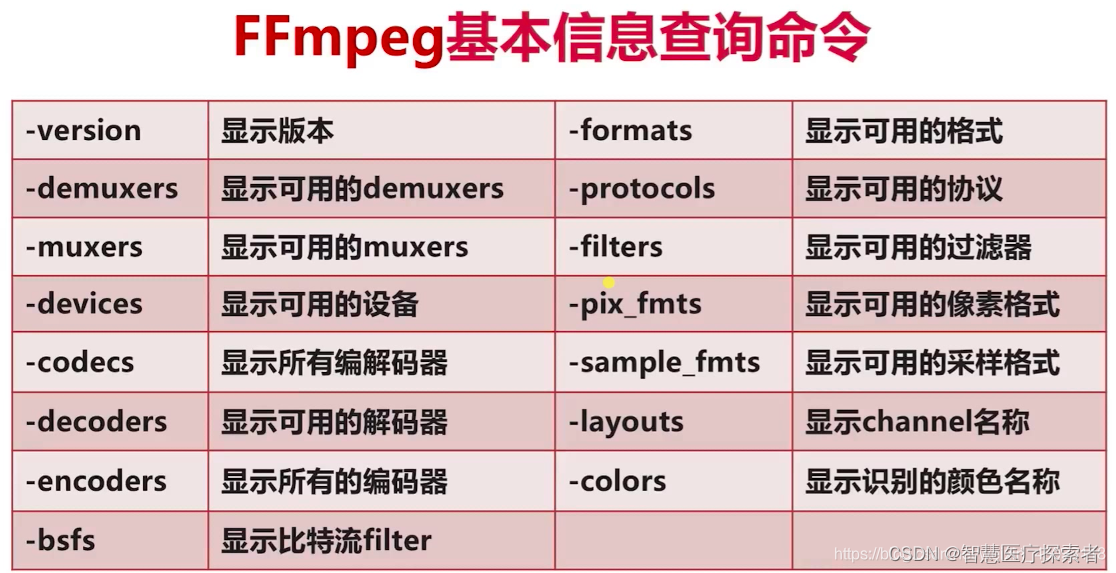
使用ffmpeg命令进行视频格式转换
1 ffmpeg介绍 FFmpeg 是一个非常强大和灵活的开源工具集,用于处理音频和视频文件。它提供了一系列的工具和库,可以用于录制、转换、流式传输和播放音频和视频。 FFmpeg 主要特点如下: 格式支持广泛:FFmpeg 支持几乎所有的音频和视…...
)
Mac安装Adobe AE/pr/LR/ai/ps/au/dw/id 2024/2023报错问题解决(常见错误:已损坏/2700/146/130/127)
1.打开允许“允许任何来源” 如何打开允许任何来源?在 Finder 菜单栏选择 【前往】 – 【实用工具 】,找到【终端】程序,双击打开,在终端窗口中输入:sudo spctl --master-disable 输入代码后,按【return …...

Python三级 每周练习题31
如果你感觉有收获,欢迎给我微信扫打赏码 ———— 以激励我输出更多优质内容 练习一: 作业1:编写程序,在下面的字典中找出身高137的同学并输出姓名,如果没找到, 输出没有 a{‘小赵’:136,‘小钱’:141,‘小孙’:146,‘小李’:13…...
【DataSophon】大数据服务组件之Flink升级
🦄 个人主页——🎐开着拖拉机回家_Linux,大数据运维-CSDN博客 🎐✨🍁 🪁🍁🪁🍁🪁🍁🪁🍁 🪁🍁🪁&am…...

Android笔记(十八):面向Compose组件结合Retrofit2和Rxjava3实现网络访问
一、Retrofit2 Square公司推出的Retrofit2库(https://square.github.io/retrofit/),改变了网络访问的方式。它实现了网络请求的封装。Retrofit库采用回调处理方式,使得通过接口提交请求和相应的参数的配置,就可以获得…...

mybatis中oracle的sql没走索引导致特别慢(未加jdbcType的)
如果直接跑sql是能走索引很快,在mybatis中不能,可能就是jdbcType的原因。 比如,我有一个属性A,在表里面是VARCHAR2类型,但是在mybatis中的sql是#{a},缺少jdbcTypeJdbcType.VARCHAR,就会导致myba…...
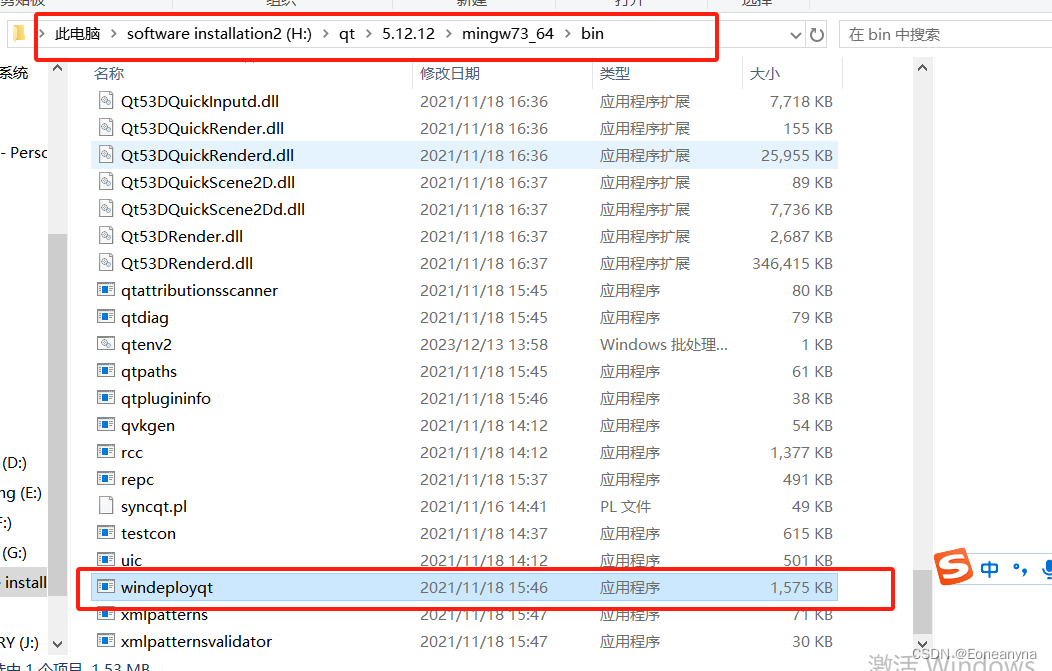
QT自带打包问题:无法定位程序输入点?metaobject@qsound
文章目录 无法定位程序输入点?metaobjectqsound……检查系统环境变量的配置:打包无须安装qt的文件 无法定位程序输入点?metaobjectqsound…… 在执行release打包程序后,相应的release文件夹下的exe文件,无法打开 如有错误欢迎指出 检查系…...

7.3 lambda函数
一、语法 1.基础语法 [capture](paramLists) mutable ->retunType{statement} capture。捕获列表,用于捕获前文的变量供lambda函数中使用,可省略。(paramLists)。参数列表,可省略。mutable。lambda表达式默认具有常量性,可以…...
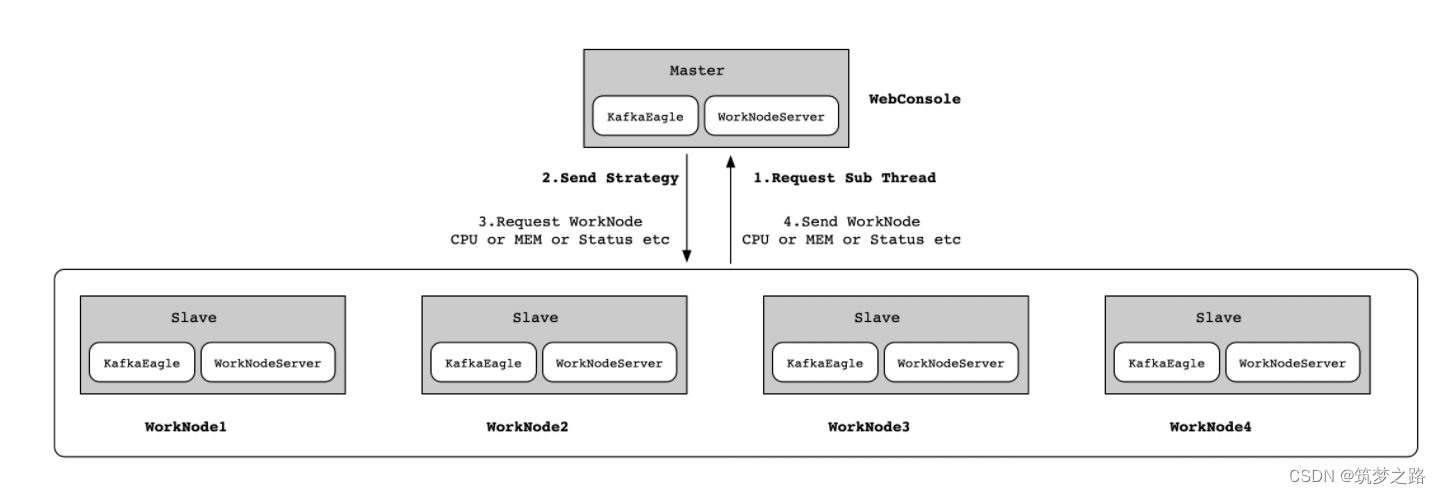
dcoker-compose一键部署EFAK —— 筑梦之路
简介 EFAK(Eagle For Apache Kafka,以前称为 Kafka Eagle)是一款由国内公司开源的Kafka集群监控系统,可以用来监视kafka集群的broker状态、Topic信息、IO、内存、consumer线程、偏移量等信息,并进行可视化图表展示。独…...

音视频:Ubuntu下安装 FFmpeg 5.0.X
1.安装相关依赖 首可选一: sudo apt-get update sudo apt-get install build-essential autoconf automake libtool pkg-config \libavcodec-dev libavformat-dev libavutil-dev \libswscale-dev libresample-dev libavdevice-dev \libopus-dev libvpx-dev libx2…...
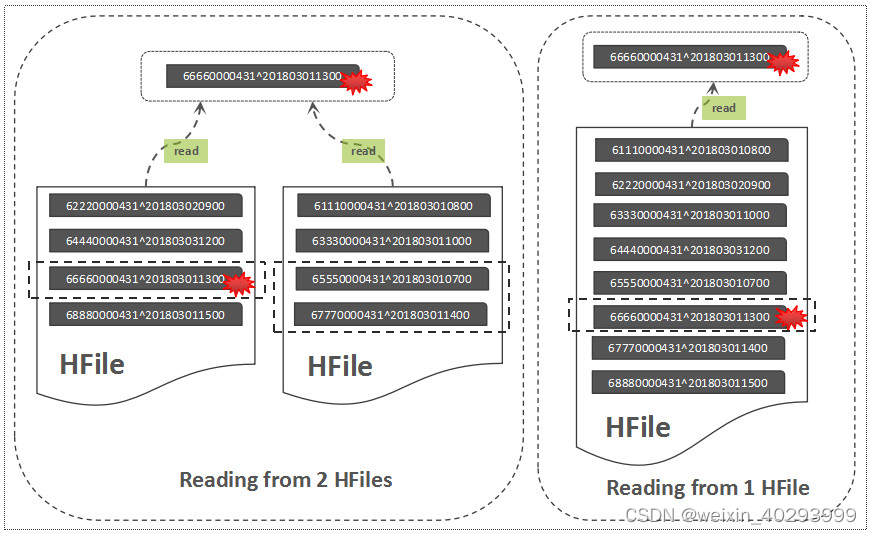
【LSM tree 】Log-structured merge-tree 一种分层、有序、面向磁盘的数据结构
文章目录 前言基本原理读写流程写流程读流程 写放大、读放大和空间放大优化 前言 LSM Tree 全称是Log-structured merge-tree, 是一种分层,有序,面向磁盘的数据结构。其核心原理是磁盘批量顺序写比随机写性能高很多,可以通过围绕这一原理进行…...
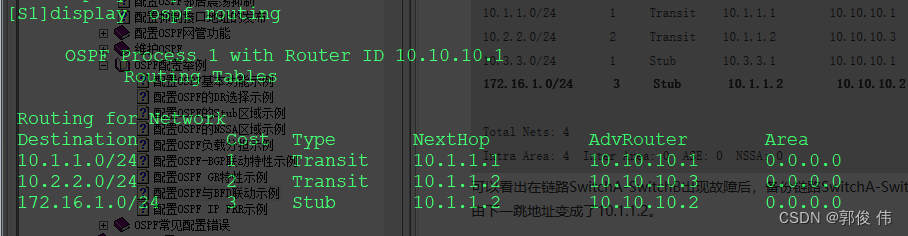
配置OSPF与BFD联动示例
定义 双向转发检测BFD(Bidirectional Forwarding Detection)是一种用于检测转发引擎之间通信故障的检测机制。 BFD对两个系统间的、同一路径上的同一种数据协议的连通性进行检测,这条路径可以是物理链路或逻辑链路,包括隧道。 …...

01到底应该怎么理解“平均负载”
1、如何了解系统的负载情况? 每次发现系统变慢时, 我们通常做的第⼀件事, 就是执⾏top或者uptime命令, 来了解系统的负载情况。 ⽐如像下⾯这样, 我在命令⾏⾥输⼊了uptime命令, 系统也随即给出了结果。 …...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
