凸优化问题求解
这里写目录标题
- 1. 线性规划基本定理
- 2.单纯形法
- 2.1 转轴运算
- 3. 内点法
- 3.1 线性规划的内点法
1. 线性规划基本定理
首先我们指出,线性规划均可等价地化成如下标准形式 { min c T x , s . t A x = b , x ⪰ 0 , \begin{align}\begin{cases}\min~c^Tx,\\\mathrm{s.t}~Ax=b,\\x\succeq0,&\end{cases}\end{align} ⎩ ⎨ ⎧min cTx,s.t Ax=b,x⪰0,其中, A = [ a 1 , ⋯ , a n ] ∈ R m × n , b ∈ R m , c ∈ R n A=[a_1,\cdots,a_n]\in\mathbb{R}^{m\times n},b\in\mathbb{R}^m,c\in\mathbb{R}^n A=[a1,⋯,an]∈Rm×n,b∈Rm,c∈Rn不妨恒假定矩阵 A A A 是行满秩的,即 r a n k ( A ) = m \mathbf{rank}(A)=m rank(A)=m(否则根据线性代数的理论,可以找到 r a n k ( A ) \mathbf{rank}(A) rank(A) 行方程来替换原方程,同时为了叙述简便,分别称矩阵 A A A 和 向量 b b b 为(1)的系数矩阵和右端向量.
因为线性规划的可行集是一个多面体,并且目标函数是线性的,从几何上直观地看,线性函数在多面体上的极小点若存在,则必然在多面体的顶点上取得.对于标准形式的线性规划问题,其最小值点必在坐标轴上达到,于是这就需要研究 A x = b Ax = b Ax=b 的所谓基础解的性质.
对标准形式的线性规划问题(7.1.1), 设方程组 A x = b Ax=b Ax=b 有解. 设 b ∈ s p a n ( A ) , { a j } j ∈ J b\in\mathbf{span}(A),\{a_j\}_{j\in J} b∈span(A),{aj}j∈J 是 A A A的列向量的一个极大线性无关组,其中 J ⊂ { 1 , . . . , n } , ∣ J ∣ = m ( ∣ J ∣ J\subset \{ 1, ..., n\} , |J|= m( |J| J⊂{1,...,n},∣J∣=m(∣J∣ 表示集合 J J J 所含元素个数).那么 b b b 必可表示为 { a j } j ∈ J \{a_j\}_{j\in J} {aj}j∈J 的线性组合.
定义 1.1 (线性方程组的基础解) 设 A ∈ R m × n , b ∈ R m , x = ( x 1 , . . . , x n ) T A\in\mathbb{R}^{m\times n},\:b\in\mathbb{R}^m,\:x=(x_1,...,x_n)^T A∈Rm×n,b∈Rm,x=(x1,...,xn)T 是线性方程组 A x = b Ax=b Ax=b 的一个解.如果存在 J ⊂ { 1 , ⋯ , n } , ∣ J ∣ = r a n k ( A ) J\subset\{1,\cdots,n\},\quad|J|=\mathbf{rank}(A) J⊂{1,⋯,n},∣J∣=rank(A),使得 x j = 0 , ∀ j ∉ J ; { a j ∣ j ∈ J } 线性无关 , x_j=0,\quad\forall j\not\in J;\quad\{a_j|j\in J\}\text{线性无关}, xj=0,∀j∈J;{aj∣j∈J}线性无关,则称 x x x 为一个基础解, x x x 的分量 { x j ∣ j ∈ J } \{x_j|j\in J\} {xj∣j∈J} 称为相应的基变量,并称 { x j ∣ j ∉ J } \{x_j|j\not\in J\} {xj∣j∈J} 为非基变量.若 { x j ∣ j ∈ J } \{x_j|j\in J\} {xj∣j∈J} 含有零元素,则称 x x x 是一个退化的基础解.
显然,若 A x = b Ax=b Ax=b 有解,则矩阵 A A A 的列向量 { a 1 , . . . , a n } \{a_1,...,a_n\} {a1,...,an} 的每一个极大线性无关组对应于一个基础解,由于 { a 1 , . . . , a n } \{a_1,...,a_n\} {a1,...,an} 的极大线性无关组未必唯一,所以 A x = b Ax=b Ax=b 的基础解也不一定是唯一的.
引理 1.1 设 A = [ a 1 , . . . , a n ] ∈ R m × n , b ∈ R m , x ∈ R n A=[a_1,...,a_n]\in\mathbb{R}^{m\times n},\:b\in\mathbb{R}^m,\:x\in\mathbb{R}^n A=[a1,...,an]∈Rm×n,b∈Rm,x∈Rn 是 A x = b Ax=b Ax=b 的一个解,那么 x x x 是基础解当且仅当 { a j ∣ x j ≠ 0 } \{a_j|x_j\neq0\} {aj∣xj=0} 线性无关.
证. 设 x x x 是基础解,根据线性方程组基础解的定义,存在 J ⊂ { 1 , ⋯ , n } , ∣ J ∣ = r a n k ( A ) J\subset\{1,\cdots,n\},\quad|J|=\mathbf{rank}(A) J⊂{1,⋯,n},∣J∣=rank(A),使得 x j = 0 , ∀ j ∉ J ; { a j ∣ j ∈ J } 线性无关 , x_j=0,\quad\forall j\not\in J;\quad\{a_j|j\in J\}\text{线性无关}, xj=0,∀j∈J;{aj∣j∈J}线性无关,于是由集合的性质可以得到, { a j ∣ x j ≠ 0 } ⊂ { a j ∣ j ∈ J } \{a_j|x_j\neq0\}\subset\{a_j|j\in J\} {aj∣xj=0}⊂{aj∣j∈J}, 所以 { a j ∣ x j ≠ 0 } \{a_j|x_j\neq0\} {aj∣xj=0} 是极大线性无关组的子集,故线性无关.
反之,设 A x = b Ax=b Ax=b 且 { a j ∣ x j ≠ 0 } \{a_j|x_j\neq0\} {aj∣xj=0} 线性无关.不妨设
{ x j ≠ 0 j = 1 , ⋯ , k ; x j = 0 j = k + 1 , ⋯ , n . \begin{cases}x_j\neq0&j=1,\cdots,k;\\x_j=0&j=k+1,\cdots,n.\end{cases} {xj=0xj=0j=1,⋯,k;j=k+1,⋯,n.因为 a 1 , . . . , a k a_1,...,a_k a1,...,ak 线性无关,所以 k ≤ m = r a n k ( A ) k\leq m= \mathbf{rank}(A) k≤m=rank(A). 当 k < m k<m k<m 时从 a k + 1 , ⋯ , a n a_{k+1},\cdots,a_n ak+1,⋯,an 中挑选 m − k m-k m−k 个向量,不妨设为 a k + 1 , ⋯ , a m a_{k+1},\cdots,a_m ak+1,⋯,am,使得 a 1 , ⋯ , a m a_1,\cdots,a_m a1,⋯,am 线性无关. 由于 x m + 1 = . . . = x n = 0 x_{m+1}=...=x_n= 0 xm+1=...=xn=0,所以 x x x 是 A x = b Ax=b Ax=b 的一个基础解.
n n n 维线性方程组 A x = b Ax=b Ax=b 的解 x x x的全体构成 R n \mathbb{R} ^n Rn 中的一个仿射集. 其基础解是落在某个 m m m 维子空间的解,它使得 { a j ∣ x j ≠ 0 } \{a_j|x_j\neq0\} {aj∣xj=0} 线性无关.
定义 1.2 (基础可行解和基础最优解) 对于线性规划(1)即 { min c T x , s . t A x = b , x ⪰ 0 , \begin{aligned}\begin{cases}\min~c^Tx,\\\mathrm{s.t}~Ax=b,\\x\succeq0,&\end{cases}\end{aligned} ⎩ ⎨ ⎧min cTx,s.t Ax=b,x⪰0,设 x x x 是 A x = b Ax=b Ax=b 的一个基础解,
(1) 若 x x x 还是(1)的一个可行点,即 x ⪰ 0 x\succeq0 x⪰0, 则称之为(1)的一个基础可行解;
(2) 若 x x x 还是(1)的一个最优解,则称之为(1)的一个基础最优解.
对于线性规划(7.1.1),有
命题 1.2 (线性规划基本定理) 对于线性规划(1)有
(1) 若存在可行点,则必存在基础可行解;
(2) 若存在最优解,则存在基础最优解
证.设 A = [ a 1 , ⋯ , a n ] ∈ R m × n , b ∈ R m , x A=[a_1,\cdots,a_n]\in\mathbb{R}^{m\times n},b\in\mathbb{R}^m,x A=[a1,⋯,an]∈Rm×n,b∈Rm,x 是(1)的一个可行点.若 { a j ∣ x j > 0 } \{a_j|x_j>0\} {aj∣xj>0} 线性相关,不妨设 x x x 的前 k k k 个分量非零: x j > 0 , j = 1 , ⋯ , k ; x j = 0 , j = k + 1 , ⋯ , n . \begin{aligned}x_j>0,&&j=1,\cdots,k;&&x_j=0,&&j=k+1,\cdots,n.\end{aligned} xj>0,j=1,⋯,k;xj=0,j=k+1,⋯,n.由于 { a j ∣ x j > 0 } \{a_j|x_j>0\} {aj∣xj>0} 线性相关,于是存在 0 ≠ y = ( y 1 , ⋯ , y k , 0 , ⋯ , 0 ) T ∈ R n 0\neq y=(y_1,\cdots,y_k,0,\cdots,0)^T\in\mathbb{R}^n 0=y=(y1,⋯,yk,0,⋯,0)T∈Rn, 使得 A y = y 1 a 1 + ⋯ + y k a k = 0. Ay=y_1a_1+\cdots+y_ka_k=0. Ay=y1a1+⋯+ykak=0.易见,当 ϵ > 0 \epsilon>0 ϵ>0 充分小时,有
\quad (a) x j ± ϵ y j > 0 , j = 1 , ⋯ , k x_j\pm \epsilon y_j> 0, j= 1, \cdots , k xj±ϵyj>0,j=1,⋯,k.所以 x ± ϵ y x\pm\epsilon y x±ϵy 都是可行点;
\quad (b) 若 x x x 是最优解,则 c T x ≤ c T ( x ± ϵ y ) c^Tx\leq c^T(x\pm\epsilon y) cTx≤cT(x±ϵy),即 c T y = 0 c^Ty=0 cTy=0. 从而 c T ( x ± ϵ y ) = c T x . c^T(x\pm\epsilon y)=c^Tx. cT(x±ϵy)=cTx.
不妨设 y 1 , . . . , y k y_1,...,y_k y1,...,yk 中至少有一个为正的项. 下面我们用用逐步逼近的思想,来让可行解 x x x 其中一个分量变为零后但仍为可行解.
让 ϵ \epsilon ϵ 逐步增大,直到 { x j − ϵ y j ∣ j = 1 , . . . , k } \{x_j-\epsilon y_j|j=1,...,k\} {xj−ϵyj∣j=1,...,k} 中至少有一项为 0 而其余各项非负. 因为 ϵ \epsilon ϵ 充分小,于是 x ~ : = x − ϵ y \tilde{x}:=x-\epsilon y x~:=x−ϵy 仍是一个可行点,且它比 x x x 至少多出一个为零的分量.
若 { a j ∣ x ~ j > 0 } \{a_j|\tilde{x}_j>0\} {aj∣x~j>0} 仍线性相关,不断重复上述逐步逼近的操作,那么有限次后便得到可行点 x ~ \tilde{x} x~, 使得 { a j ∣ x ~ j > 0 } \{a_j|\tilde{x}_j>0\} {aj∣x~j>0} 线性无关(因为线性方程组 A x = b Ax=b Ax=b的 系数矩阵 A A A 的秩不为0).因为 0 ⪯ x 0\preceq x 0⪯x,所以 { a j ∣ x ~ j > 0 } = { a j ∣ x ~ j ≠ 0 } \{a_j|\tilde{x}_j>0\}=\{a_j|\tilde{x}_j\neq0\} {aj∣x~j>0}={aj∣x~j=0}, 于是由引理 1.1可知, x ~ \tilde{x} x~ 是一个基础可行解. (1) 获证.
命题 1.2是非常重要的,它能够说明在整个可行集中求解线性规划(1)的问题可以归结为在基础可行集中求解.而 A x = b Ax=b Ax=b 的基础解个数就是 { a 1 , . . . , a n } \{a_1,...,a_n\} {a1,...,an} 的极大线性无关组的个数,且最大个数为 ( n m ) \binom{n}{m} (mn).
定义 1.3 (极点) 设 x ∈ S ⊂ R n x\in S\subset\mathbb{R}^n x∈S⊂Rn. 如果不存在互异的 x 1 , x 2 ∈ S x_1,x_2\in S x1,x2∈S 以及 0 < θ < 1 0<\theta<1 0<θ<1, 使得 x = θ x 1 + ( 1 − θ ) x 2 x=\theta x_1+(1-\theta)x_2 x=θx1+(1−θ)x2,即线段 x 1 x 2 x_1x_2 x1x2之间任意一点都不属于集合 S S S ,则称 x x x 是 S S S 的一个极点.
命题 1.3 (基础可行解的几何特征) 设 A ∈ R m × n , b ∈ R m A\in\mathbb{R}^{m\times n},\quad b\in\mathbb{R}^m A∈Rm×n,b∈Rm,记 D : = { x ∈ R n ∣ A x = b , x ⪰ 0 } \mathcal{D}:=\{x\in\mathbb{R}^n|Ax=b,\:x\succeq0\} D:={x∈Rn∣Ax=b,x⪰0}.那么, x x x 是一个基础可行解当且仅当它是 D D D 的一个极点.
证.设 x x x 不是 D \mathcal{D} D 的一个极点,不妨设 x ∈ D ( x\in\mathcal{D}( x∈D(否则已经不是基础可行解). 因为 x x x是基础可行解且 x x x 不是极点,于是存在 y , z ∈ D , y ≠ z y,z\in\mathcal{D},\:y\neq z y,z∈D,y=z,以及 0 < θ < 1 0<\theta<1 0<θ<1, 使得 x = θ y + ( 1 − θ ) z x=\theta y+(1-\theta)z x=θy+(1−θ)z.不妨设设 { i ∣ x i > 0 } = { 1 , . . . , k } . \{i|x_i>0\}=\{1,...,k\}. {i∣xi>0}={1,...,k}. 由于 x , y , z x,y,z x,y,z 的所有分量都是非负的,且由于 x = θ y + ( 1 − θ ) z x=\theta y+(1-\theta)z x=θy+(1−θ)z,所以 y , z y,z y,z 的后 n − k n-k n−k 个分量也是 0. 于是 ∑ i = 1 k ( y i − z i ) a i = ∑ i = 1 k y i a i − ∑ i = 1 k z i a i = A y − A z = b − b = 0. \sum_{i=1}^k(y_i-z_i)a_i=\sum_{i=1}^ky_ia_i-\sum_{i=1}^kz_ia_i=Ay-Az=b-b=0. i=1∑k(yi−zi)ai=i=1∑kyiai−i=1∑kziai=Ay−Az=b−b=0.所以 a 1 , . . . , a k a_1,...,a_k a1,...,ak 线性相关. 由 引理 1.1可知, x x x 不是一个基础可行解,矛盾
反之,设 x x x 不是一个基础可行解但 x x x是极点,不妨设 x ∈ D ( x\in\mathcal{D}( x∈D(否则它已经不是 D \mathcal{D} D 的极点). 由于 x x x 不是基础可行解,则 x x x 也不是 A x = b Ax=b Ax=b 的基础解. 不妨设 { i ∣ x i > 0 } = { 1 , . . . , k } \{i|x_i>0\}=\{1,...,k\} {i∣xi>0}={1,...,k}, 那么 a 1 , . . . , a k a_1,...,a_k a1,...,ak 线性相关. 于是存在 0 ≠ y = ( y 1 , ⋯ , y k , 0 , ⋯ , 0 ) T 0\neq y=(y_1,\cdots,y_k,0,\cdots,0)^T 0=y=(y1,⋯,yk,0,⋯,0)T, 使得 A y = 0 Ay=0 Ay=0. 易见当 ϵ \epsilon ϵ 充分小时,有 x ± ϵ y ∈ D , x = 1 2 [ ( x + ϵ y ) + ( x − ϵ y ) ] . x\pm\epsilon y\in\mathcal{D},\quad x=\frac{1}{2}\big[(x+\epsilon y)+(x-\epsilon y)\big]. x±ϵy∈D,x=21[(x+ϵy)+(x−ϵy)].所以 x x x 不是 D \mathcal D D 的极点,矛盾.
2.单纯形法
单纯形法的基本思想是从线性规划的一个基础可行解出发,寻找另一个基础可行解,并在此过程中使目标函数不断下降,直至达到基础最优解.
2.1 转轴运算
转轴运算是单纯形算法的基本运算单元,现考虑如下标准形式的线性规划 { min f ( x ) = c T x + d s . t A x = b , x ⪰ 0 , \begin{align}\begin{cases}&\min f(x)=c^Tx+d\\ &\mathrm{s.t}Ax=b,\\&x\succeq0,&\end{cases}\end{align} ⎩ ⎨ ⎧minf(x)=cTx+ds.tAx=b,x⪰0, 其中 A ∈ R m × n , b ∈ R m , c ∈ R n . 下面先介绍单纯形表和三种基本变换 . \text{其中 }A\in\mathbb{R}^{m\times n},\mathrm{~}b\in\mathbb{R}^m,\mathrm{~}c\in\mathbb{R}^n.\text{ 下面先介绍单纯形表和三种基本变换}. 其中 A∈Rm×n, b∈Rm, c∈Rn. 下面先介绍单纯形表和三种基本变换.构造如下所示的图表: [ x T b A b c T − d ] = [ x 1 ⋯ x p ⋯ x q ⋯ x n b a 11 ⋯ a 1 p ⋯ a 1 q ⋯ a 1 n b 1 ⋮ ⋮ ⋮ ⋮ ⋮ a m 1 ⋯ a m p ⋯ a m q ⋯ a m n b m c 1 ⋯ c p ⋯ c q ⋯ c n − d ] , \begin{align}\left.\left[\begin{array}{c|c}x^T&b\\\hline A&b\\\hline c^T&-d\end{array}\right.\right]=\left[\begin{array}{cccccc|c}x_1&\cdots&x_p&\cdots&x_q&\cdots&x_n&b\\\hline a_{11}&\cdots&a_{1p}&\cdots&a_{1q}&\cdots&a_{1n}&b_1\\\vdots&&\vdots&&\vdots&&\vdots&\vdots\\a_{m1}&\cdots&a_{mp}&\cdots&a_{mq}&\cdots&a_{mn}&b_m\\\hline c_1&\cdots&c_p&\cdots&c_q&\cdots&c_n&-d\end{array}\right],\end{align} xTAcTbb−d = x1a11⋮am1c1⋯⋯⋯⋯xpa1p⋮ampcp⋯⋯⋯⋯xqa1q⋮amqcq⋯⋯⋯⋯xna1n⋮amncnbb1⋮bm−d ,并且称之为线性规划(2)的单纯形表.其中第一行且并非数值或变量,称之为标记行,其作用是在后续列交换时过程中标记对应变量的位置.最后一行是线性规划(1)的目标函数的系数,称之为目标行.而除标记行和目标行以外的部分是矩阵 [ A , b ] [A, b] [A,b],为叙述简便,对 1 ≤ i ≤ m 1 ≤ i ≤ m 1≤i≤m,仍称矩阵 [ A , b [A, b [A,b] 的第 i i i 行为单纯形表的第 i i i 行.
(2.1.1) 变量置换, 设 1 ≤ p < q ≤ n 1 ≤ p<q ≤ n 1≤p<q≤n 将单纯性表(3)的第 p p p 列与第 q q q 列进行交换,可以得到如下新的单纯性表 [ x ′ T b A ′ b ′ c ′ T − d ′ ] = [ x 1 ⋯ x q ⋯ x p ⋯ x n b a 11 ⋯ a 1 q ⋯ a 1 p ⋯ a 1 n b 1 ⋮ ⋮ ⋮ ⋮ ⋮ a m 1 ⋯ a m q ⋯ a m p ⋯ a m n b m c 1 ⋯ c q ⋯ c p ⋯ c n − d ] . \left.\left[\begin{array}{c|c}x'^T&b\\\hline A'&b'\\\hline c'^T&-d'\end{array}\right.\right]=\left[\begin{array}{cccccc|c}x_1&\cdots&x_q&\cdots&x_p&\cdots&x_n&b\\\hline a_{11}&\cdots&a_{1q}&\cdots&a_{1p}&\cdots&a_{1n}&b_1\\\vdots&&\vdots&&\vdots&&\vdots&\vdots\\a_{m1}&\cdots&a_{mq}&\cdots&a_{mp}&\cdots&a_{mn}&b_m\\\hline c_1&\cdots&c_q&\cdots&c_p&\cdots&c_n&-d\end{array}\right]. x′TA′c′Tbb′−d′ = x1a11⋮am1c1⋯⋯⋯⋯xqa1q⋮amqcq⋯⋯⋯⋯xpa1p⋮ampcp⋯⋯⋯⋯xna1n⋮amncnbb1⋮bm−d .根据线性代数的内容,有 x ′ = Q x , A ′ = A Q T , b ′ = b , c ′ = Q c , d ′ = d , x'=Qx,\quad A'=AQ^T,\quad b'=b,\quad c'=Qc,\quad d'=d, x′=Qx,A′=AQT,b′=b,c′=Qc,d′=d,其中 Q Q Q 是交换第 p p p 行和第 q q q 行的 n n n 阶置换矩阵, x x x 是 n n n 维列向量,即 x = ( x 1 , x 2 , ⋯ , x n ) T x=(x_1,x_2,\cdots,x_n)^T x=(x1,x2,⋯,xn)T,由此可得 A x = b ⟺ A ′ x ′ = b ′ . Ax=b\iff A^{\prime}x^{\prime}=b^{\prime}. Ax=b⟺A′x′=b′.
(2.1.2) 行初等变换, 将单纯性表(3)除标记行和目标行以外的各行进行矩阵的行初等
变换,得到新的单纯形表X.显然标记行和目标行不会改变-,仅仅是将 [ A , b ] [A, b] [A,b] 变成了 [ A ′ , b ′ ] X [A′, b′]X [A′,b′]X 显然 A x = b Ax = b Ax=b 同解于 A ′ x = b ′ A′x = b′ A′x=b′
(2.1.3) 目标函数变形:设 1 ≤ i ≤ m , λ ∈ R 1\leq i\leq m,\lambda\in\mathbb{R} 1≤i≤m,λ∈R.将单纯性表(7.2.2)的目标行减去 [ A , b ] [A,b] [A,b] 的第 i i i 行的 λ倍,得到新的目标行 [ c ′ , − d ′ ] [c^{\prime},-d^{\prime}] [c′,−d′]. 记目标函数 f ( x ) : = c T x + d f(x):=c^Tx+d f(x):=cTx+d ,那么,这相当于用 c T x = f ( x ) − d c^Tx=f(x)-d cTx=f(x)−d 减去 A x = b Ax=b Ax=b 的 i i i 行的 入倍,得 c ′ T x = f ( x ) − d − λ b i c^{\prime T}x=f(x)-d-\lambda b_i c′Tx=f(x)−d−λbi, 即
3. 内点法
3.1 线性规划的内点法
内点法的基本思想
单纯形法从顶点到顶点搜索最优解- 当初始点远离最优解时- 需要很长的搜索代价X 而内
点法在可行域内部进行搜索迭代的算法X 设当前点 x0 是可行集 D 的一个相对内点- 根
据 优化问题笔记 中的引理 1.2.1,设 x ∗ ∈ D x^*\in\mathcal{D} x∗∈D,那么 S F D ( x ∗ ) \mathbf{SFD}(x^*) SFD(x∗) 是一个闭集,且当 x ∗ ∈ r i ( D ) x^*\in\mathbf{ri}(\mathcal{D}) x∗∈ri(D) 时,有 V P ∩ ∂ B ( 0 , 1 ) ⊂ F D ( x ∗ ) V_{\mathcal{P}}\cap\partial B(0,1)\subset\mathbf{FD}(x^*) VP∩∂B(0,1)⊂FD(x∗),因而 c l ( F D ( x ∗ ) ) ⊂ S F D ( x ∗ ) ⊂ U ( x ∗ ) ∩ ∂ B ( 0 , 1 ) ⊂ V D ∩ ∂ B ( 0 , 1 ) \mathbf{cl}(\mathbf{FD}(x^{*}))\subset\mathbf{SFD}(x^{*})\subset\mathbf{U}(x^{*})\cap\partial B(0,1)\subset V_{\mathcal{D}}\cap\partial B(0,1) cl(FD(x∗))⊂SFD(x∗)⊂U(x∗)∩∂B(0,1)⊂VD∩∂B(0,1)中四个集合均相等,
相关文章:

凸优化问题求解
这里写目录标题 1. 线性规划基本定理2.单纯形法2.1 转轴运算 3. 内点法3.1 线性规划的内点法 1. 线性规划基本定理 首先我们指出,线性规划均可等价地化成如下标准形式 { min c T x , s . t A x b , x ⪰ 0 , \begin{align}\begin{cases}\min~c^Tx,\\\mathrm{s.…...
文件操作入门指南
目录 一、为什么使用文件 二、什么是文件 2.1 程序文件 2.2 数据文件 2.3 文件名 三、文件的打开和关闭 3.1 文件指针 3.2 文件的打开和关闭 四、文件的顺序读写 编辑 🌻深入理解 “流”: 🍂文件的顺序读写函数介绍: …...

Axure之交互与情节与一些实例
目录 一.交互与情节简介 二.ERP登录页到主页的跳转 三.ERP的菜单跳转到各个页面的跳转 四.省市联动 五.手机下拉加载 今天就到这里了,希望帮到你哦!!! 一.交互与情节简介 "交互"通常指的是人与人、人与计算机或物体…...
)
【数据库设计和SQL基础语法】--连接与联接--多表查询与子查询基础(二)
一、子查询基础 1.1 子查询概述 子查询是指在一个查询语句内部嵌套另一个查询语句的过程。子查询可以嵌套在 SELECT、FROM、WHERE 或 HAVING 子句中,用于从数据库中检索数据或执行其他操作。子查询通常返回一个结果集,该结果集可以被包含它的主查询使用…...
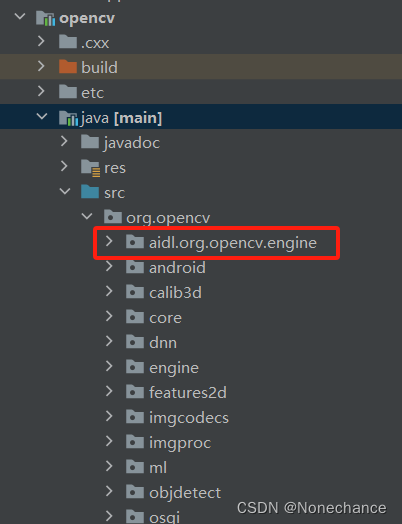
Android studio中导入opencv库
具体opencv库的导入流程参考链接:Android Studio开发之路 (五)导入OpenCV以及报错解决 一、出现的错误:NullPointerException: Cannot invoke “java.io.File.toPath()” because “this.mySdkLocation” is null 解决办法&#…...
_基础知识)
Linux(1)_基础知识
第一部分 一、Linux系统概述 创始人:芬兰大学大一的学生写的Linux内核,李纳斯托瓦兹。 Linux时unix的类系统; 特点:多用户 多线程的操作系统; 开源操作系统; 开源项目:操作系统,应用…...

网络相关面试题
简述 TCP 连接的过程(淘系) 参考答案: TCP 协议通过三次握手建立可靠的点对点连接,具体过程是: 首先服务器进入监听状态,然后即可处理连接 第一次握手:建立连接时,客户端发送 syn 包…...

Vue2面试题:说一下对跨域的理解?
http请求分为两大类:普通http请求(如百度请求)和ajax请求(跨域是出现在ajax请求) 同源策略:在浏览器发起ajax请求时,当前的网址和被请求的网址协议、域名、端口号必须完全一致,目的是…...

Axure中如何使用交互样式交互事件交互动作情形
🎬 艳艳耶✌️:个人主页 🔥 个人专栏 :《产品经理如何画泳道图&流程图》 ⛺️ 越努力 ,越幸运 目录 一、Axure中交互样式 1、什么是交互样式? 2、交互样式的作用? 3、Axure中如何…...
)
1112. 迷宫(DFS之连通性模型)
1112. 迷宫 - AcWing题库 一天Extense在森林里探险的时候不小心走入了一个迷宫,迷宫可以看成是由 n∗n 的格点组成,每个格点只有2种状态,.和#,前者表示可以通行后者表示不能通行。 同时当Extense处在某个格点时,他只…...
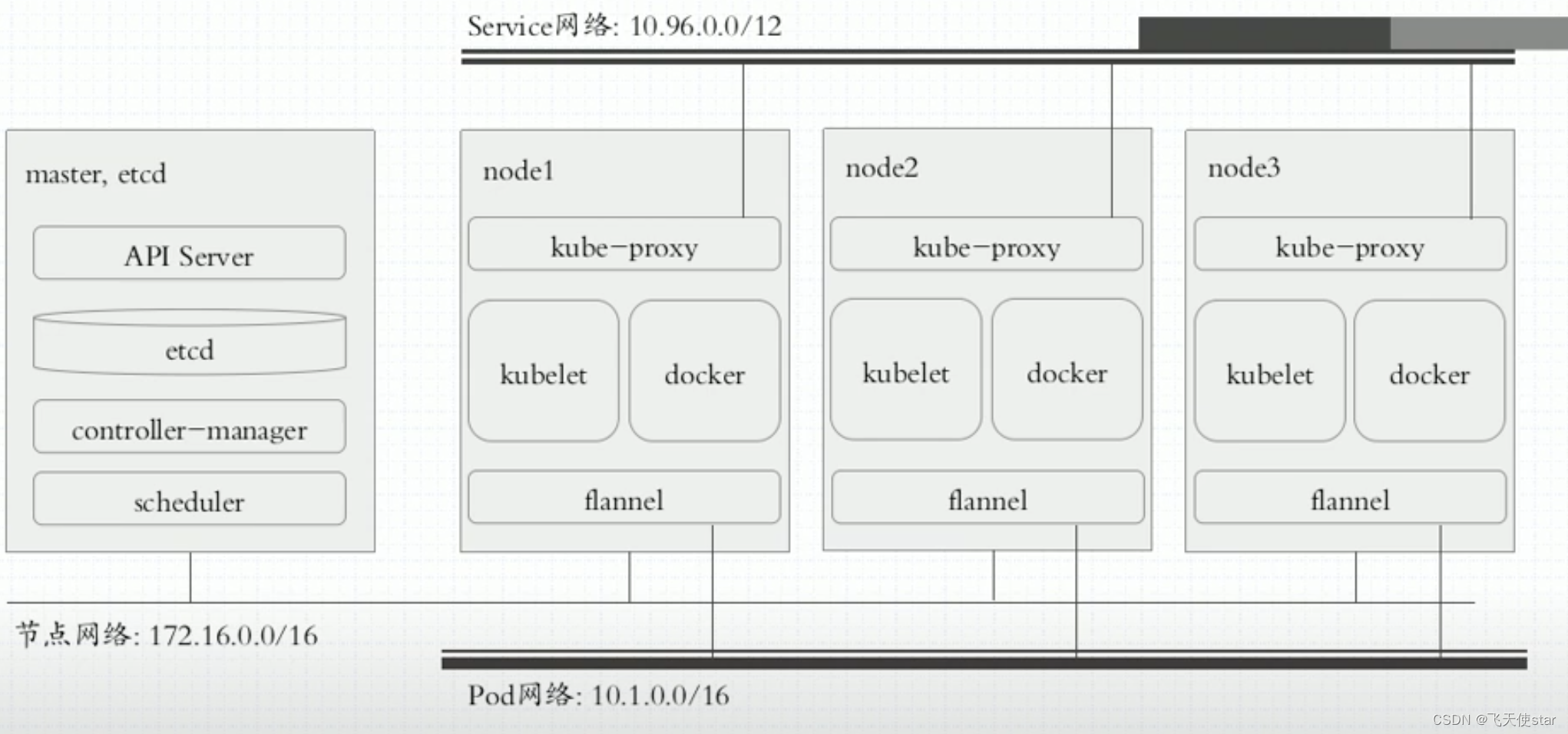
飞天使-k8s知识点1-kubernetes架构简述
文章目录 名词功能要点 k8s核心要素CNCF 云原生框架简介k8s组建介绍 名词 CI 持续集成, 自动化构建和测试:通过使用自动化构建工具和自动化测试套件,持续集成可以帮助开发人员自动构建和测试他们的代码。这样可以快速检测到潜在的问题,并及早…...
linux中deadline调度原理与代码注释
简介 deadline调度是比rt调度更高优先级的调度,它没有依赖于优先级的概念,而是给了每个实时任务一定的调度时间,这样的好处是:使多个实时任务场景的时间分配更合理,不让一些实时任务因为优先级低而饿死。deadline调度…...

jquery、vue、uni-app、小程序的页面传参方式
jQuery、Vue、Uni-app 和小程序(例如微信小程序)都有它们自己的页面传参方式。下面分别介绍这几种方式的页面传参方式: jQuery: 在jQuery中,页面传参通常是通过URL的查询参数来实现的。例如: <a href"page2…...
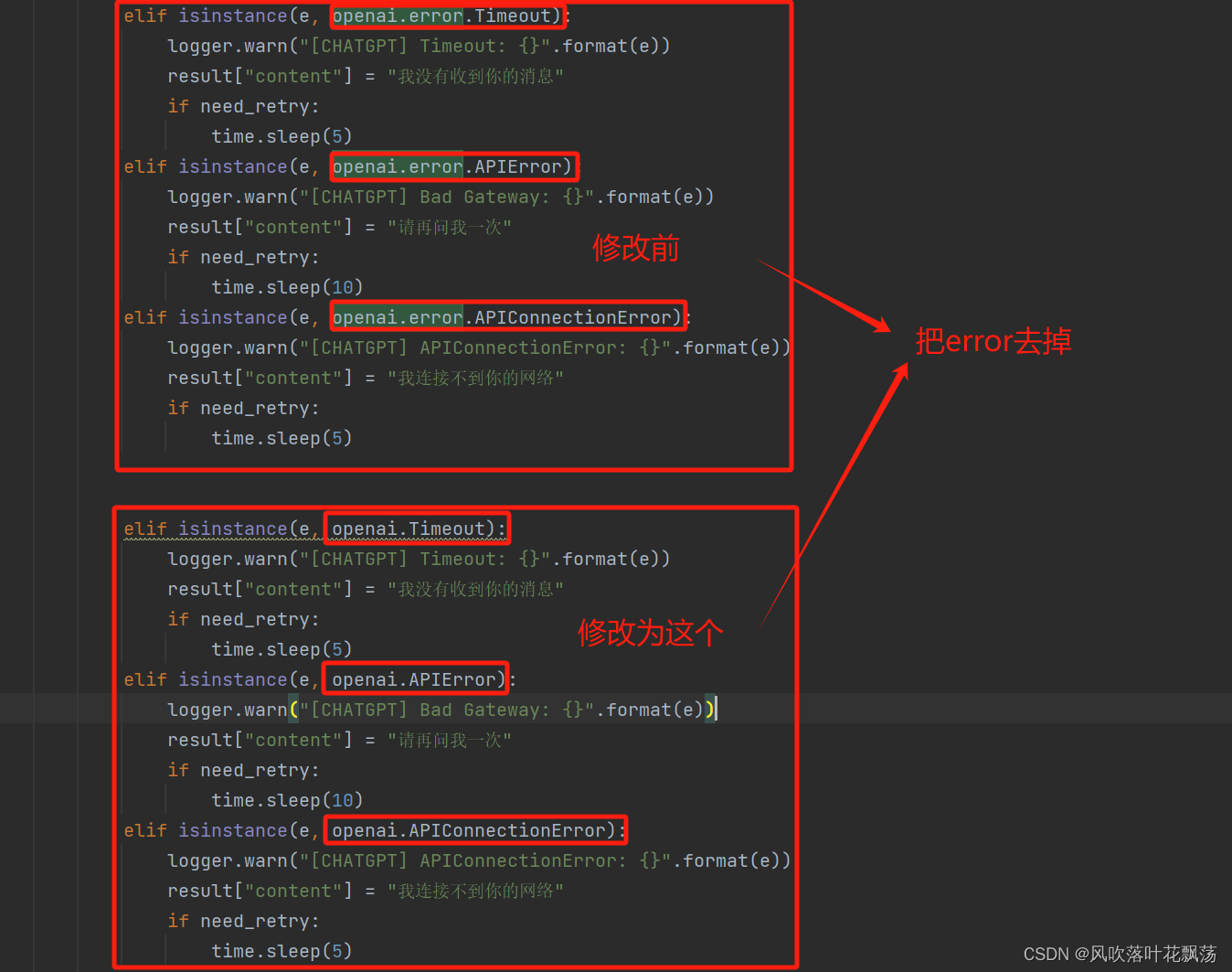
ModuleNotFoundError: No module named ‘openai.error‘
ModuleNotFoundError: No module named ‘openai.error’ result self.fn(*self.args, **self.kwargs) File “H:\chatGPTWeb\chatgpt-on-wechat\channel\chat_channel.py”, line 168, in _handle reply self._generate_reply(context) File “H:\chatGPTWeb\chatgpt-on-wec…...

理解pom.xml中的parent标签
✅作者简介:大家好,我是Leo,热爱Java后端开发者,一个想要与大家共同进步的男人😉😉 🍎个人主页:Leo的博客 💞当前专栏: 循序渐进学SpringBoot ✨特色专栏&…...
element ui el-avatar 源码解析零基础逐行解析
avatar功能介绍 快捷配置头像的样式 avatar 的参数配置 属性说明参数size尺寸type string 类型 (‘large’,‘medium’,‘small’)number类型 validator 校验shape形状circle (原型) square(方形)icon传入的iconsrc传入的图片st…...
Linux下c语言实现动态库的动态调用
在Linux操作系统下,有时候需要在不重新编译程序的情况下,运行时动态地加载库,这时可以通过Linux操作系统提供的API可以实现,涉及到的API主要有dlopen、dlsym和dlclose。使用时,需要加上头文件#include <dlfcn.h>…...
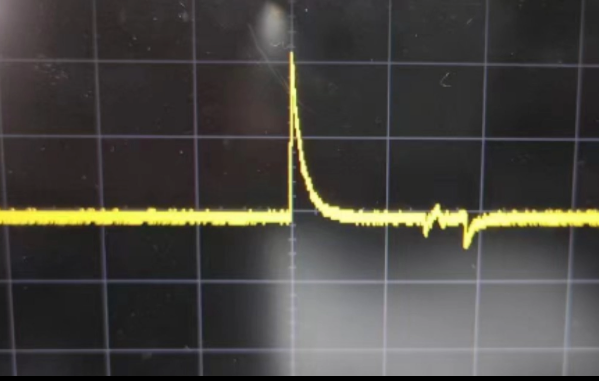
为什么MCU在ADC采样时IO口有毛刺?
大家在使用MCU内部ADC进行信号采样一个静态电压时,可能在IO口上看到这样的波形。这个时候大家一般会认识是信号源有问题,但仔细观察会发现这个毛刺的频率是和ADC触发频率一样的。 那么为什么MCU在ADC采样时IO口会出现毛刺呢?这个毛刺对结果有…...

C# 将 Word 转化分享为电子期刊
目录 需求 方案分析 相关库引入 关键代码 Word 转 Pdf Pdf 转批量 Jpeg Jpeg 转为电子书 实现效果演示 小结 需求 曾经的一个项目,要求实现制作电子期刊定期发送给企业进行阅读,基本的需求如下: 1、由编辑人员使用 Microsoft Word…...

网络世界的黑暗角落:常见漏洞攻防大揭秘
网络世界的黑暗角落:常见漏洞攻防大揭秘 今天带来了网站常见的漏洞总结,大家在自己的服务器上也需要好好进行防护,密码不要过于简单.不然非常容易遭到攻击,最终达到不可挽回的损失.很多黑客想网络乞丐一样将你服务器打宕机,然后要求你进行付费.不知道大家有没有遇到…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...
