no module named cv2 、numpy 、xxx超全解决方案
常规解决方案可见博客:
https://blog.csdn.net/ALiLiLiYa/article/details/126988014
案例
上述仍没有解决,可以参考如下进行:
例如:明明文件夹存在下述文件,仍然报错。那么可能缺少环境变量导致。
No module named 'torchvision.edgeailite'
解决方案1:
export PYTHONPATH=:$PYTHONPATH:yourfile/path/edgeai/torchvision
注意:
将yourfile/path/edgeai/torchvision替换为你的文件路径
解决方案2
主动添加环境变量
import sys
sys.path.append('/path/to/my/module')
'/path/to/my/module’替换为你确实文件的路径
总结:
sys.path 注意1
在 Python 中,sys.path 是一个包含 Python 解释器在导入模块时搜索路径的列表。默认情况下,sys.path 会包含以下几个路径:
- 空字符串(表示当前目录)
- Python 安装目录
- PYTHONPATH 环境变量中指定的路径
- 操作系统特定的目录
如果您想添加自定义路径到 sys.path 中,可以使用 sys.path.append() 方法。该方法接受一个路径作为参数,并将其添加到 sys.path 的末尾。例如:
import sys
sys.path.append('/path/to/my/module')
在这个例子中,我们将 /path/to/my/module 路径添加到 sys.path 中。这将使得 Python 解释器在导入模块时也会搜索该路径。这对于导入自己编写的模块或第三方模块非常有用。
需要注意的是,sys.path 的顺序很重要。Python 解释器会按照 sys.path 中出现的顺序来搜索模块。因此,如果您同时拥有与 Python 标准库同名的模块,那么 Python 可能会首先找到您自己编写的模块,而不是标准库中的模块。所以您需要确保添加到 sys.path 中的路径不会与其他已存在的路径中的模块命名产生冲突。
注意2PYTHONPATH
在这个命令中,您尝试使用export命令将一个路径添加到PYTHONPATH环境变量中。PYTHONPATH是一个告诉Python解释器在哪里搜索模块的环境变量。在这个命令中,使用了$PYTHONPATH来引用当前PYTHONPATH的值,并使用:来分隔不同的路径。
然而,这个命令有一个错误:在将新路径添加到PYTHONPATH时,冒号前面没有指定任何路径。冒号实际上用于分隔不同的路径,在这里表示将当前的PYTHONPATH添加到新路径之前。因此,应该将这个命令修改为:
export PYTHONPATH=$PYTHONPATH:/yourfile/path/edgeai/torchvision
这样做将会把/yourfile/path/edgeai/torchvision添加到当前PYTHONPATH的末尾,使得Python解释器在搜索模块时也会查找这个路径。
请注意,这个命令只在当前的shell会话中有效。如果您希望每次启动shell时都设置这个环境变量,可以将这个命令添加到您的shell配置文件(比如~/.bashrc或~/.zshrc)中。
希望这些信息对您有所帮助。如果您还有其他问题,请随时提出。
相关文章:

no module named cv2 、numpy 、xxx超全解决方案
常规解决方案可见博客: https://blog.csdn.net/ALiLiLiYa/article/details/126988014 案例 上述仍没有解决,可以参考如下进行: 例如:明明文件夹存在下述文件,仍然报错。那么可能缺少环境变量导致。 No module named …...
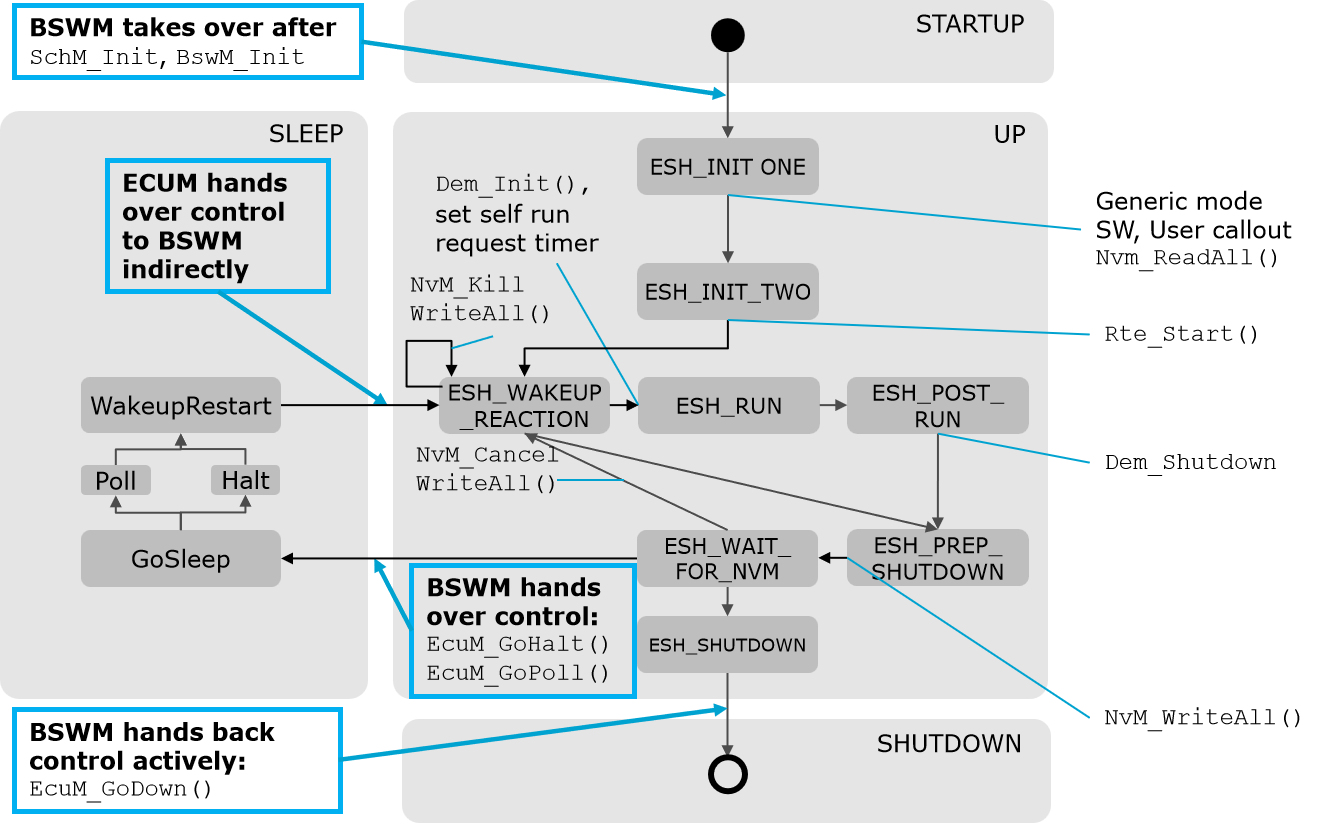
BSWM 模式管理(二)ESH
BSWM 模式管理 ESH 1 ECU State Handling (ESH)2 BSWM ESH 五大模式与六大通用状态机3 状态机对应的切换条件 conditions or rules4 默认主要的 ACTION 或者 ACTION LIST1 ECU State Handling (ESH) 与 ECUM 相关,整个 ECU 状态管理的状态机制 2 BSWM ESH 五大模式与六大通…...
mac电脑安装虚拟机教程
1、准备一台虚拟机,安装CentOS7 常用的虚拟化软件有两种: VirtualBoxVMware 这里我们使用VirtualBox来安装虚拟机,下载地址:Downloads – Oracle VM VirtualBox 001 点击安装 002 报错:he installer has detected an…...

手动配置 kafka 用户密码,认证方式等的方式
场景 部分场景会指定使用某一kafka 来提高安全性,这里就不得不使用用户密码认证方式等来控制 方法示例 // 手动加载配置信息private Map<String, Object> consumerConfigs() {Map<String, Object> props new HashMap<>();props.put(ConsumerCo…...
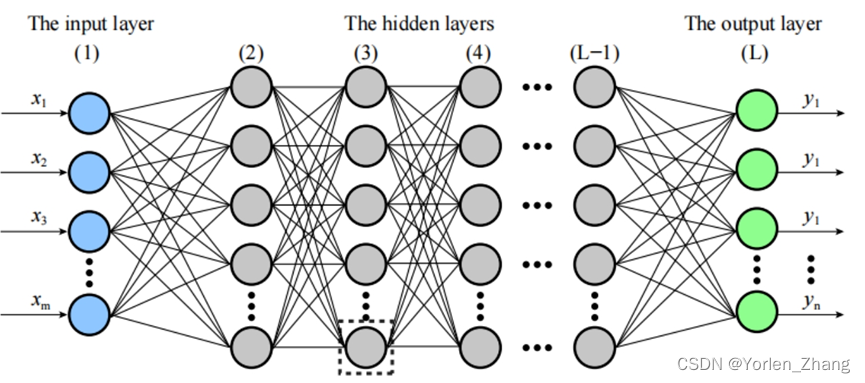
机器学习 深度学习 神经网络
神经网络概念: 神经网络是一个由生物神经元组成的网络或电路,或者从现代意义上讲,是一个由人工神经元或节点组成的人工神经网络。因此,一个神经网络要么是由生物神经元组成的生物神经网络,要么是用于解决人工智能&…...
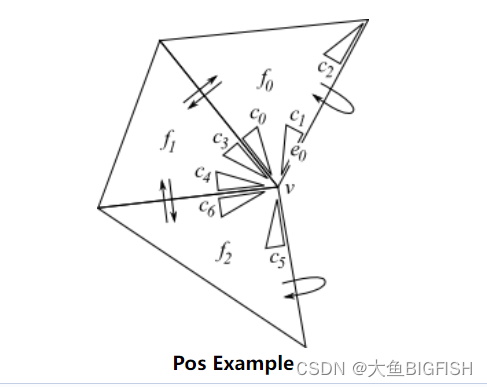
VCG 获取某个顶点的邻接顶点
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 与之前的思路相同,这里我们利用VCG为我们提供的拓扑结构,获取某个顶点的邻接顶点,这在我们处理网格数据时往往很有用。 二、实现代码 //VCG #include <vcg/complex/algorithms/create/platonic.h> #inclu…...

四川云汇优想教育咨询有限公司电商服务靠谱吗
随着抖音电商的兴起,越来越多的商家开始关注这一领域。四川云汇优想教育咨询有限公司作为一家专注于电商服务的企业,也受到了广泛的关注。那么,四川云汇优想教育咨询有限公司的抖音电商服务靠谱吗?下面我们将从多个方面进行深入剖…...

Spring MVC框架支持RESTful,设计URL时可以使用{自定义名称}的占位符@Get(“/{id:[0-9]+}/delete“)
背景:在开发实践中,如果没有明确的规定URL,可以参考: 传统接口 获取数据列表,固定接口路径:/数据类型的复数 例如:/albums/select RESTful接口 - 根据ID获取某条数据:/数据类型的复数/{id} - 例…...
【GoLang】哪些大公司正在使用Go语言
你见过哪些令你膛目结舌的代码技巧? 文章目录 你见过哪些令你膛目结舌的代码技巧?前言:哪些大公司正在使用Go语言谷歌(Google):脸书(Facebook):亚马逊(Amazon…...
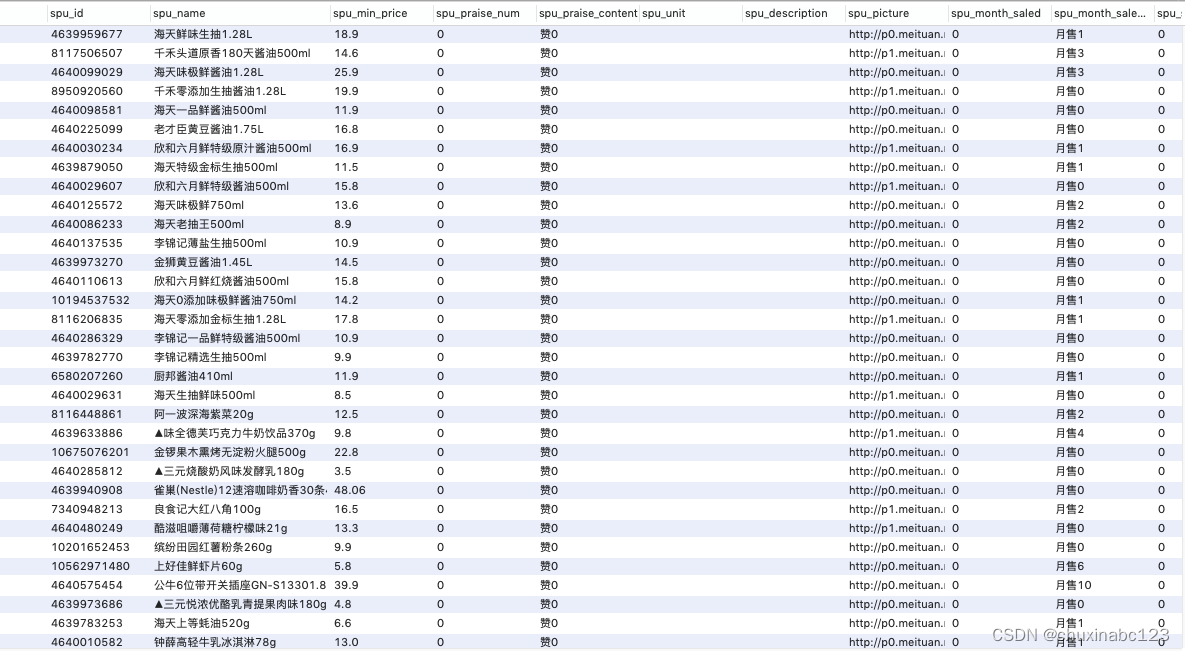
美团外卖商超商品销量数据
美团外卖商超商品月销量 字段名 店铺id 店铺名称 商品id 商品名称 商品分类 规格名 原价 现价 月销 规格属性 描述 商品图片 含商家月销量...

【C++高阶(八)】单例模式特殊类的设计
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:C从入门到精通⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学习C 🔝🔝 单例模式 1. 前言2. 设计一个不能被拷贝/继承的…...
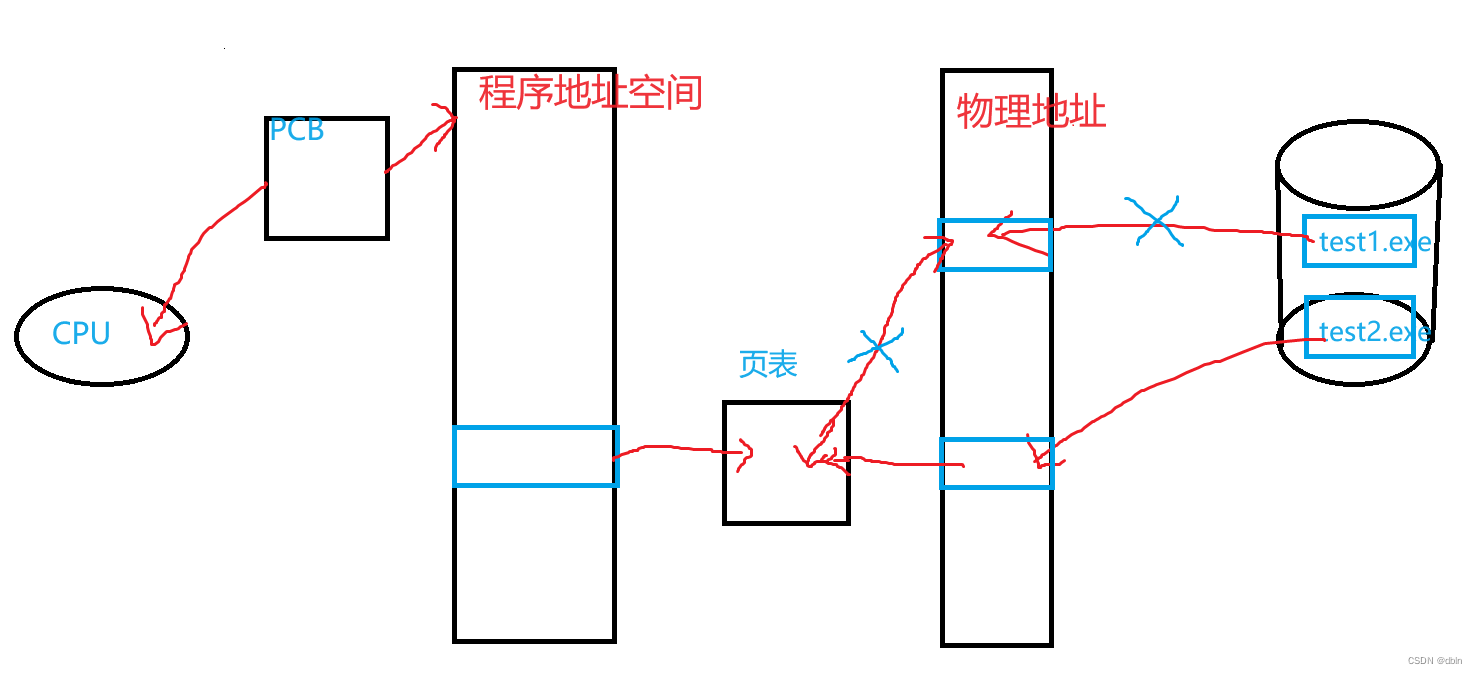
Linux之进程(五)(进程控制)
目录 一、进程创建 1、fork函数创建进程 2、fork函数的返回值 3、fork常规用法 4、fork调用失败的原因 二、进程终止 1、进程终止的方式 2、进程退出码 3、进程的退出方法 三、进程等待 1、进程等待的必要性 2、wait函数 3、waitpid函数 四、进程程序替换 1、概念…...

63. 不同路径 II 23.12.21(二)
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。 现在考虑网格中有障碍物。那么从左上角到右下角…...

【线性代数】两个向量组等价,其中一个向量组线性无关,另一个向量组也是线性无关吗?
一、问题 两个向量组等价,其中一个向量组线性无关,另一个向量组也是线性无关吗? 二、答案 不一定,当两个向量组中的向量个数也相同时,结论才成立.若向量个数不相同,结论不成立. 例如: 向量组一:(1,0),(0,1) 向量组二:(1,0),(0,1),(1,1) 两…...

c语言:指针作为参数传递
探究实参与形参它们相互独立 由于主调函数的变量a,b与被调函数的形参x,y它们相互独立。函数 swap 可以修改变量x,y,但是却无法影响到主调函数中的a,b。 现在利用取地址运算符,分别打印它们的首地址&#x…...

YOLOv5性能评估指标->mAP、Precision、Recall、FPS、Confienc (讲解论文关注的主要指标)
简介 这篇博客,主要给大家讲解我们在训练yolov5时生成的结果文件中各个图片及其中指标的含义,帮助大家更深入的理解,以及我们在评估模型时和发表论文时主要关注的参数有那些。本文通过举例训练过程中的某一时间的结果来帮助大家理解…...

陶建辉在 CIAS 2023 谈“新能源汽车的数字化”
近年,中国的新能源汽车发展迅猛,在全球竞争中表现出色,已经连续 8 年保持全球销量第一。在新兴技术的推动下,新能源汽车的数字化转型也正在加速进行,从汽车制造到能源利用、人机交互,各个环节都在进行数字化…...
PSP - 结构生物学中的机器学习 (NIPS MLSB Workshop 2023.12)
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://spike.blog.csdn.net/article/details/135120094 Machine Learning in Structural Biology (机器学习在结构生物学中) 网址:https://www.mlsb.io/ Workshop at the 37th Co…...

某领先的集成电路研发中心:建立跨网交换平台 杜绝数据泄露风险
1、客户介绍 某技术领先的集成电路研发中心,是产学研合作的国家级集成电路研发中心,致力于解决重大共性技术的研发及服务支撑问题。该中心积极探索国际化道路,不断提升国际影响力,与多家国际著名集成电路企业和研发机构建立技术合…...

map|动态规划|单调栈|LeetCode975:奇偶跳
作者推荐 【贪心算法】【中位贪心】.执行操作使频率分数最大 涉及知识点 单调栈 动态规划 map 题目 给定一个整数数组 A,你可以从某一起始索引出发,跳跃一定次数。在你跳跃的过程中,第 1、3、5… 次跳跃称为奇数跳跃,而第 2、…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...
