C语言——高精度乘法
一、引子
高精度乘法相较于高精度加法和减法有更多的不同,加法和减法是一位对应一位进行操作的,而乘法是一个数的每一位对另一个数的每一位进行操作,需要的计算步骤更多。
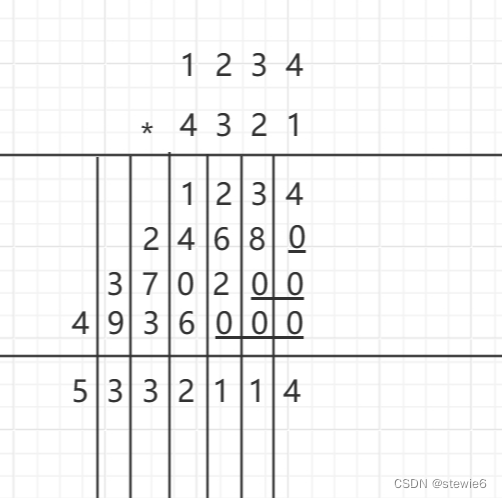
二、核心算法
void Calculate(int num1[], int num2[], int numres[], int len1, int len2)
{// 核心乘法算法for (int i = 0; i < len1; i++){for (int j = 0; j < len2; j++){numres[i + j] += num1[i] * num2[j];numres[i + j + 1] += numres[i + j] / 10;numres[i + j] = numres[i + j] % 10;}}
}这一段代码是高精度乘法核心算法的实现,它模拟了我们手工进行多位数乘法的过程。这里,我们有两个数n1和n2,它们分别以字符串的形式存储,并被转换成整数数组num1和num2,其中低位在前,高位在后(即字符串“123”会被存储成整数数组{3, 2, 1})。然后我们对这两个数组执行乘法。
对于乘法,我们对于num1的每一位(由外层循环 i 控制)与num2的每一位(由内层循环 j 控制)相乘。由于我们是按位计算,所以需要考虑结果的位数(res数组的下标 i + j )。这里考虑结果的位数是最低位数,由于数组的特性,两个数字的最低位在数组中是作为第零位的,而且在数组中两个数的每一位相当于之前都是减少了一位,如果是10 * 10两个两位数相乘理论上结果是三位,但是如果将两数字的位数相加作为结果的位数,那结果就是四(2 + 2)位数,这样就不对了,但是由于数组的特性,将两数字位数相加改成两数字当前索引相加就可以了,10 * 10,索引相加是(1 + 1) = 2,而二作为索引是3位数,结果是三位数,这样就对了。在这里的原理是转换的过程,两个数的位数转成索引要减一,两个数就是减二,而结果的索引转成位数又要加一,这是就相当于减一,在前面直接用位数运算的版本中,结果是四位,这里的就相当于结果的位数减一,结果的位数就变成了三,就对了。
假设两个两位数相乘,结果的位数最低可能是三位,最高是四位,这里是按最低算的。如果放到了最高位就会导致这一步的结果扩大了十倍,对比上面的解释我们发现数组是可以直接实现将每一步结果存到正确的位上的。也就是num1[i] * num2[j]的结果可以直接放到res[i + j]里的这样是正确的。
如果不使用数组而使用数字位数的话,也就是假设 i 和 j 不是索引而是数位,那就不能将(num1的 i 位的数字) * (num2的 j 位的数字)的结果放到res的(i + j)位上,而要把结果放到res的(i + j - 1)位上。
假设是10 * 10 = 100,结果是三位,
num1[0] * num2[0]是0 * 0 = 0,res[0 + 0] = 0,res[0] = 0
num1[1] * num2[0] = 0,res[1 + 0] = 0,res[1] = 0
num1[0] * num2[1] = 0,res[0 + 1] = 0,res[1] = 0
num1[1] * num[1] = 1,res[1 + 1] = 1,res[2] = 1
这是结果就是100
这个乘法的过程是:
1. res[i + j] += n1[i] * n2[j]:这里我们将num1的第i位和num2的第 j 位相乘,然后加到结果的相应位置。由于n1和n2的下标为 i 和 j ,那么对应的结果应该是res[i + j]。这里的结果为res[i + j]就是我们上面解释的体现,用数组的特性使得这样做是正确的。
2. res[i + j + 1] += res[i + j] / 10:这里我们处理进位。如果res[i + j]的结果是两位数(即大于或等于10),我们需要将十位上的数字进位到结果的下一个位置res[i + j + 1]。
3. res[i + j] = res[i + j] % 10:保证结果数组res的每一位都是个位数,即进行模10操作。进位已经在上一步处理过了,这里确保数组res中存储的是当前位的正确数字。
这个过程会一直重复,直到num1和num2中的每一位都相乘。由于进位可能影响到最终结果的位数,结果数组res的实际使用长度可能会比num1和num2的长度总和还要大。所以,我们在定义res数组的时候要确保它有足够的空间来存储可能的最大结果,即num1长度和num2长度的和。
在乘法完成后,结果数组res中存储的是乘法结果的每一位数字,但是顺序是反的,即最低位在数组的第0个位置。在最后,我们需要将结果数组转换回字符串,并且反转回正确的顺序来输出最终的乘积。
三、处理正负
我们同时还要考虑结果的正负,对结果的正负进行判断,影响结果正负的因素是乘数的正负,这里就是同正异负,可以判断好结果的正负,然后将负号在最后打印。
在输入乘数时会有负号,所以要判断乘数是否为负数,然后还要将乘数前的负号去除,防止对之后的计算产生影响。
同时,在处理正负前不能将字符数组反转或者转成整型数组。
int JudgePorN(char arrch1[], char arrch2[])//1代表负,0代表正
{if (arrch1[0] == '-' && arrch2[0] != '-'){arrch1[0] = '0';//将 - (负号)替换为符号0,防止对后面的计算有影响,符号0在后面的计算中不会有影响,因为零会在后面作为前导零去除。注意是'0',如果写成数字0就不对了,数字0是\0的ASIIC码,写成数字0会被转换成\0,\0是字符串的结束符return 1;}else if (arrch1[0] != '-' && arrch2[0] == '-'){arrch2[0] = '0';return 1;}else if (arrch1[0] == '-' && arrch2[0] == '-'){arrch1[0] = '0';arrch2[0] = '0';return 0;}return 0;
}所以处理正负函数要在字符数组反转函数和转成整型数组函数之前调用。
四、代码实现
#include <stdio.h>
#include <string.h>void DigitReverse(char arr[])//反转字符串,以便后续计算
{int length = (int)strlen(arr);for (int i = 0; i < length / 2; i++){int temp = arr[i];arr[i] = arr[length - i - 1];arr[length - i - 1] = temp;}
}void StringTranstoNumber(char arrchar[],int arrnum[])//将字符数组转换为数字数组
{int length = (int)strlen(arrchar);for (int i = 0; i < length; i++){arrnum[i] = arrchar[i] - '0';}
}void Calculate(int num1[], int num2[], int numres[], int len1, int len2)
{// 核心乘法算法for (int i = 0; i < len1; i++){for (int j = 0; j < len2; j++){numres[i + j] += num1[i] * num2[j];numres[i + j + 1] += numres[i + j] / 10;numres[i + j] = numres[i + j] % 10;}}
}void BigNumMul(char arrch1[], char arrch2[], int res[],int len1,int len2)
{DigitReverse(arrch1);DigitReverse(arrch2);int num1[505] = {0};int num2[505] = {0};StringTranstoNumber(arrch1,num1);StringTranstoNumber(arrch1,num2);Calculate(num1,num2,res,len1,len2);//计算结果
}void Print(int resnum[],int lengthmax)//打印函数
{int i = lengthmax;while (i > 0 && resnum[i] == 0)//去除前导零,因为是按最大位数算的,可能有前导零{i--;}for (; i >= 0; i--){printf("%d",resnum[i]);}
} int JudgePorN(char arrch1[], char arrch2[])//1代表负,0代表正
{if (arrch1[0] == '-' && arrch2[0] != '-'){arrch1[0] = '0';//将 - (负号)替换为符号0,防止对后面的计算有影响,符号0在后面的计算中不会有影响,因为零会在后面作为前导零去除。注意是'0',如果写成数字0就不对了,数字0是\0的ASIIC码,写成数字0会被转换成\0,\0是字符串的结束符return 1;}else if (arrch1[0] != '-' && arrch2[0] == '-'){arrch2[0] = '0';return 1;}else if (arrch1[0] == '-' && arrch2[0] == '-'){arrch1[0] = '0';arrch2[0] = '0';return 0;}return 0;
}int main()
{char ch1[505] = "0";char ch2[505] = "0";scanf("%s",ch1);scanf("%s",ch2);int res[1010] = {0};int len1 = (int)strlen(ch1);int len2 = (int)strlen(ch2);if (len1 == 1 && ch1[0] == '0'){printf("0");}else if (len2 == 1 && ch2[0] == '0'){printf("0");}else if (len1 == 1 && len2 == 1 && ch1[0] == '0' && ch2[0] == '0'){printf("0");}else//非零情况{int judgevalue = JudgePorN(ch1, ch2);//判断结果正负并去除字符串前面的 - (负号)BigNumMul(ch1, ch2, res, len1, len2);int lengthmax = len1 + len2;//乘法结果最大可能是两个乘数的位数和if (judgevalue == 1)//结果为负{printf("-");Print(res, lengthmax);}else//结果为正{Print(res, lengthmax);}}
}相关文章:

C语言——高精度乘法
一、引子 高精度乘法相较于高精度加法和减法有更多的不同,加法和减法是一位对应一位进行操作的,而乘法是一个数的每一位对另一个数的每一位进行操作,需要的计算步骤更多。 二、核心算法 void Calculate(int num1[], int num2[], int numres…...
为什么C语言没有被C++所取代呢?
今日话题,为什么C语言没有被C所取代呢?虽然C是一个功能更强大的语言,但C语言在嵌入式领域仍然广泛使用,因为它更轻量级、更具可移植性,并且更适合在资源受限的环境中工作。这就是为什么C语言没有被C所取代的原因。如果…...
)
基于Spring的枚举类+策略模式设计(以实现多种第三方支付功能为例)
摘要 最近阅读《贯彻设计模式》这本书,里面使用一个更真实的项目来介绍设计模式的使用,相较于其它那些只会以披萨、厨师为例的设计模式书籍是有些进步。但这书有时候为了使用设计模式而强行朝着对应的 UML 图来设计类结构,并且对设计理念缺少…...

基于Linphone android sdk开发Android软话机
1.Linphone简介 1.1 简介 LinPhone是一个遵循GPL协议的开源网络电话或者IP语音电话(VOIP)系统,其主要如下。使用linphone,开发者可以在互联网上随意的通信,包括语音、视频、即时文本消息。linphone使用SIP协议&#…...
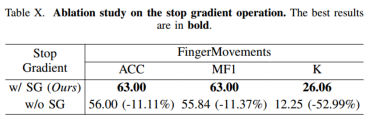
[论文分享]TimeDRL:多元时间序列的解纠缠表示学习
论文题目:TimeDRL: Disentangled Representation Learning for Multivariate Time-Series 论文地址:https://arxiv.org/abs/2312.04142 代码地址:暂无 关键要点:多元时间序列,自监督表征学习,分类和预测 摘…...
分享一个好看的vs主题
最近发现了一个很好看的vs主题(个人认为挺好看的),想要分享给大家。 主题的名字叫NightOwl,和vscode的主题颜色挺像的。操作方法也十分简单,首先我们先在最上面哪一行找到扩展。 然后点击管理扩展,再搜索栏…...

什么是云呼叫中心?
云呼叫中心作为一种高效的企业呼叫管理方案,越来越受到企业的青睐,常被用于管理客服和销售业务。那么,云呼叫中心到底是什么? 什么是云呼叫中心? 云呼叫中心是一种基于互联网的呼叫管理系统,与传统的呼叫…...
还在用nvm?来试试更快的node版本管理工具——fnm
前言 📫 大家好,我是南木元元,热衷分享有趣实用的文章,希望大家多多支持,一起进步! 🍅 个人主页:南木元元 目录 什么是node版本管理 常见的node版本管理工具 fnm是什么 安装fnm …...
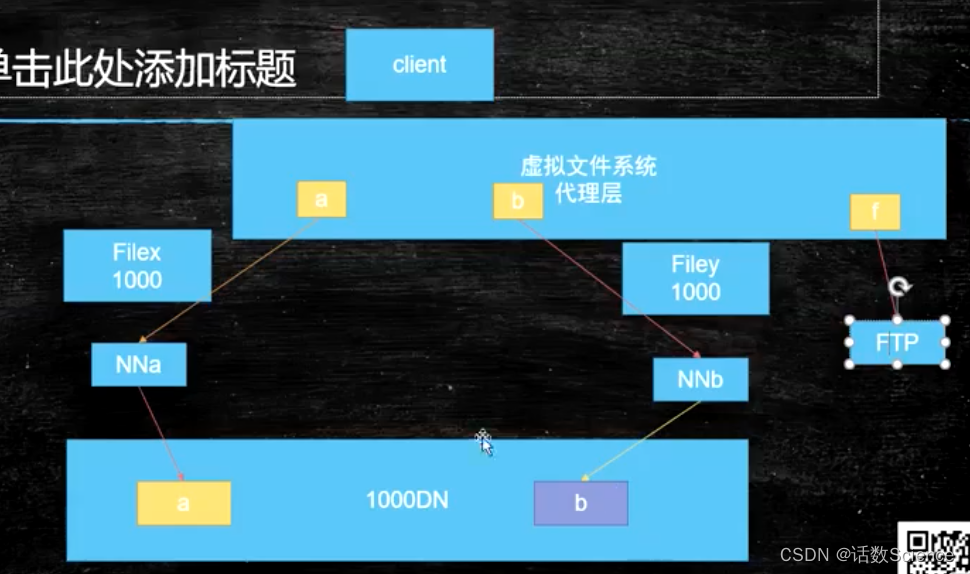
【Hadoop精讲】HDFS详解
目录 理论知识点 角色功能 元数据持久化 安全模式 SecondaryNameNode(SNN) 副本放置策略 HDFS写流程 HDFS读流程 HA高可用 CPA原则 Paxos算法 HA解决方案 HDFS-Fedration解决方案(联邦机制) 理论知识点 角色功能 元数据持久化 另一台机器就…...
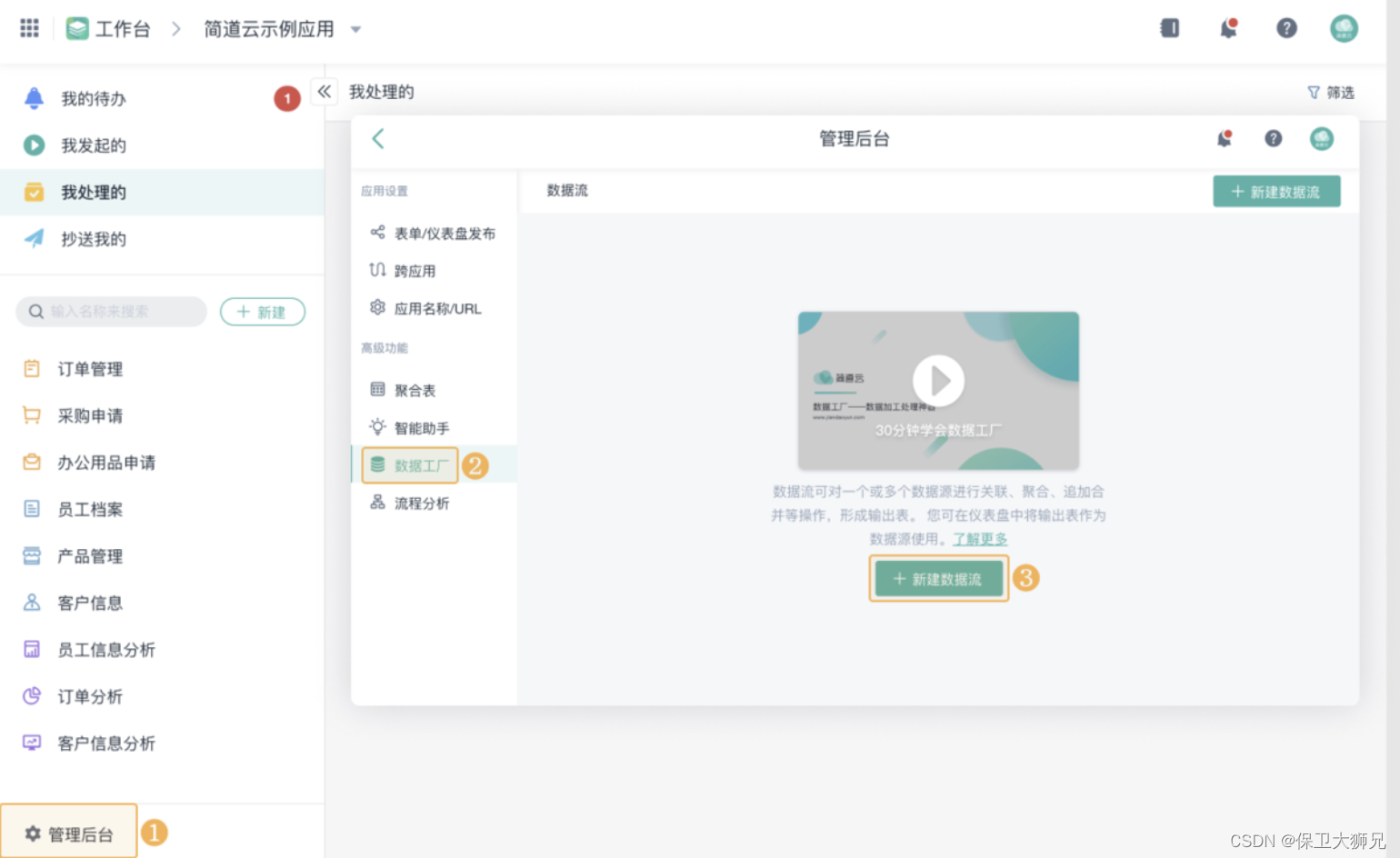
企业需要哪些数字化管理系统?
企业需要哪些数字化管理系统? ✅企业引进管理系统肯定是为了帮助整合和管理大量的数据,从而优化业务流程,提高工作效率和生产力。 ❌但是,如果各个系统之间不互通、无法互相关联数据的话,反而会增加工作量和时间成本…...
【vue】开发常见问题及解决方案
有一些问题不限于 Vue,还适应于其他类型的 SPA 项目。 1. 页面权限控制和登陆验证页面权限控制 页面权限控制是什么意思呢? 就是一个网站有不同的角色,比如管理员和普通用户,要求不同的角色能访问的页面是不一样的。如果一个页…...

飞天使-k8s知识点3-卸载yum 安装的k8s
要彻底卸载使用yum安装的 Kubernetes 集群,您可以按照以下步骤进行操作: 停止 Kubernetes 服务: sudo systemctl stop kubelet sudo systemctl stop docker 卸载 Kubernetes 组件: sudo yum remove -y kubelet kubeadm kubectl…...

ZooKeeper 集群搭建
文章目录 ZooKeeper 概述选举机制搭建前准备分布式配置分布式安装解压缩并重命名配置环境配置服务器编号配置文件 操作集群编写脚本运行脚本搭建过程中常见错误 ZooKeeper 概述 Zookeeper 是一个开源的分布式服务协调框架,由Apache软件基金会开发和维护。以下是对Z…...

Meson:现代的构建系统
Meson是一款现代化、高性能的开源构建系统,旨在提供简单、快速和可读性强的构建脚本。Meson被设计为跨平台的,支持多种编程语言,包括C、C、Fortran、Python等。其目标是替代传统的构建工具,如Autotools和CMake,提供更简…...
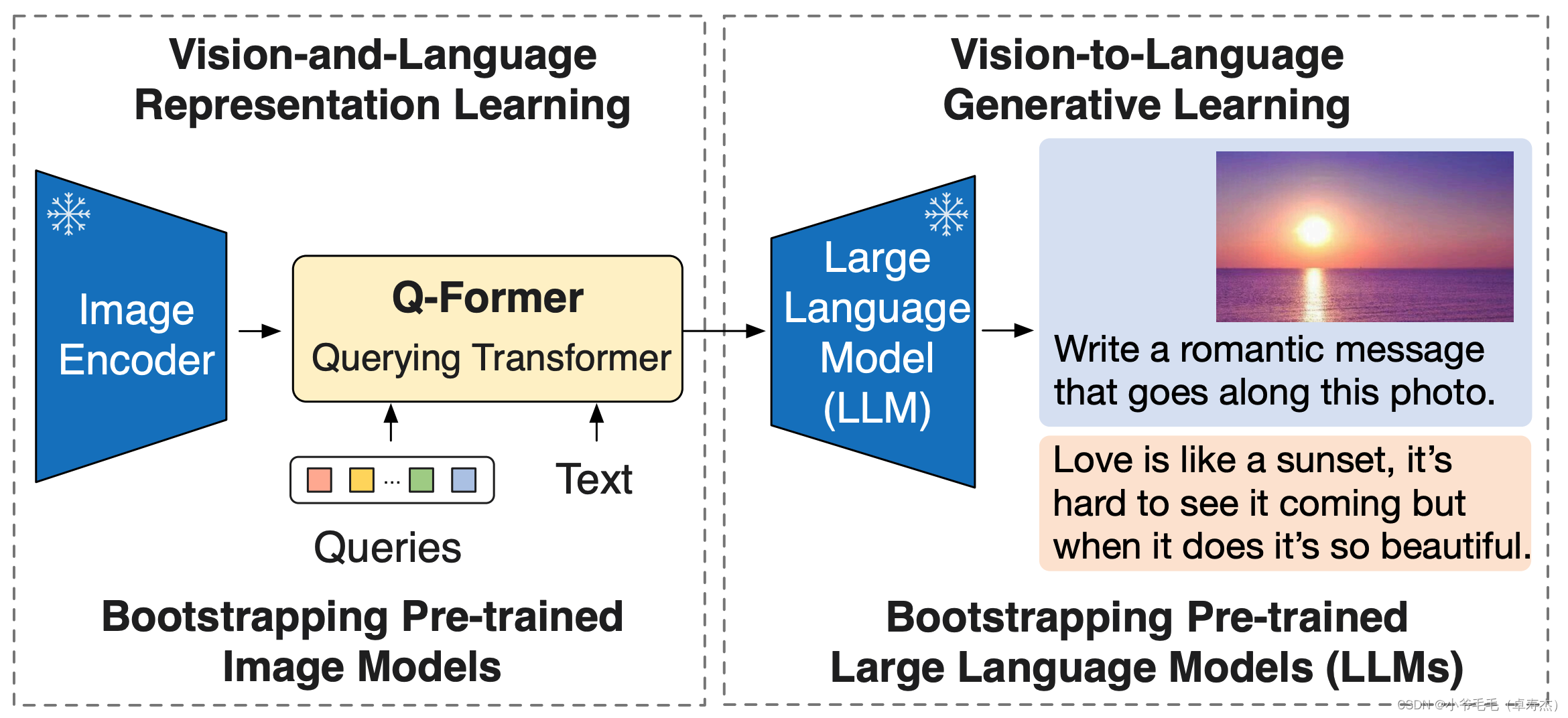
【大模型AIGC系列课程 5-2】视觉-语言大模型原理
重磅推荐专栏: 《大模型AIGC》;《课程大纲》 本专栏致力于探索和讨论当今最前沿的技术趋势和应用领域,包括但不限于ChatGPT和Stable Diffusion等。我们将深入研究大型模型的开发和应用,以及与之相关的人工智能生成内容(AIGC)技术。通过深入的技术解析和实践经验分享,旨在…...

震惊!难怪别人家的孩子越来越聪明,原来竟是因为它
前段时间工作调动给孩子换了个新学校,刚开始担心她不能适应新学校的授课方式,但任课老师对她评价很高,夸她上课很专注。 为了训练孩子的专注力,作为家长可没少下功夫,画画,下五子棋等益智游戏的兴趣班没少…...
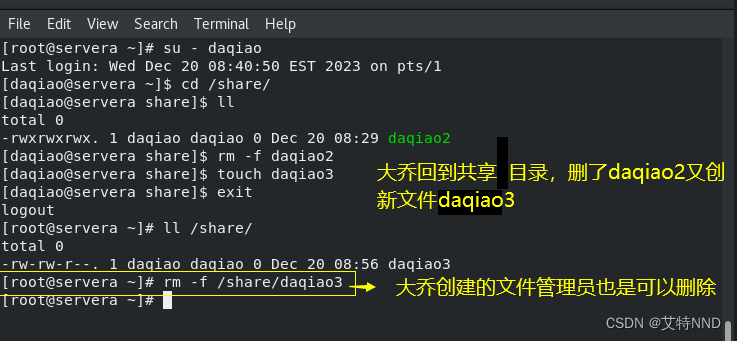
Linux操作系统(UMASK+SUID+SGID+STICK)
UMASK反掩码 如何查看反掩码:直接在终端窗口运行 umask root用户反掩码:0022 普通用户反掩码:0002 UMASK的作用:确定目录,文件的缺省权限值 以root身份创建目录,观察目录的9位权限值 以root身份创建普通文件…...

Java 中单例模式的常见实现方式
目录 一、什么是单例模式? 二、单例模式有什么作用? 三、常见的创建单例模式的方式 1、饿汉式创建 2、懒汉式创建 3、DCL(Double Checked Lock)双检锁方式创建 3.1、synchronized 同步锁的基本使用 3.2、使用 DCL 中存在的疑…...

【C语言】自定义类型之联合和枚举
目录 1. 前言2. 联合体2.1 联合体类型的声明2.2 联合体的特点2.3 相同成员的结构体和联合体对比2.4 联合体大小的计算2.4 判断当前机器的大小端 3. 枚举3.1 枚举类型的声明3.2 枚举类型的优点3.3 枚举类型的使用 1. 前言 在之前的博客中介绍了自定义类型中的结构体,…...
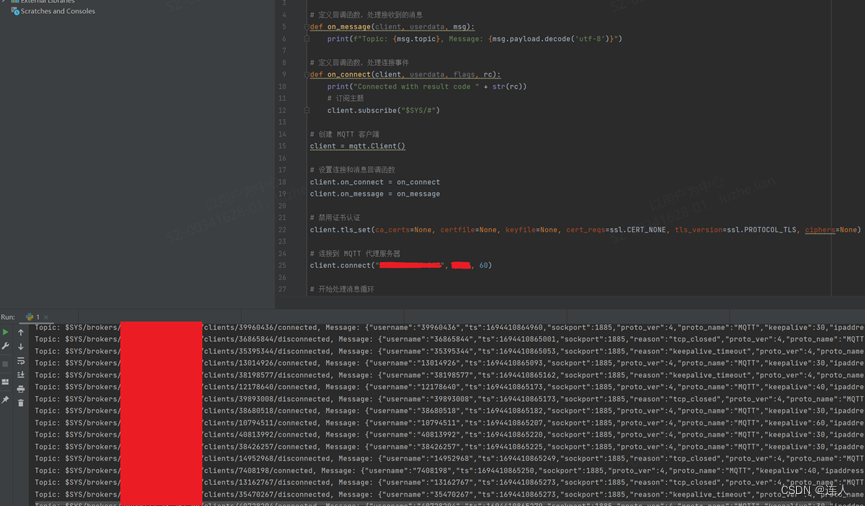
使用Mosquitto/python3进行MQTT连接
一、简介 MQTT(消息队列遥测传输)是ISO 标准(ISO/IEC PRF 20922)下基于发布/订阅范式的消息协议。它工作在 TCP/IP协议族上,是为硬件性能低下的远程设备以及网络状况糟糕的情况下而设计的发布/订阅型消息协议,为此,它需要一个消息中间件。 …...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...
