76. 最小覆盖子串。优化官方题解!
leetcode原题如下:
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。
注意:
- 对于
t中重复字符,我们寻找的子字符串中该字符数量必须不少于t中该字符数量。 - 如果
s中存在这样的子串,我们保证它是唯一的答案。
解题思路---滑动窗口
如何判断当前的窗口包含所有 t 所需的字符呢?我们可以用一个哈希表表示 t 中所有的字符以及它们的个数,用一个哈希表动态维护窗口中所有的字符以及它们的个数,如果这个动态表中包含 t 的哈希表中的所有字符,并且对应的个数都不小于 t 的哈希表中各个字符的个数,那么当前的窗口是「可行」的。
官方题解:
Map<Character, Integer> ori = new HashMap<Character, Integer>();Map<Character, Integer> cnt = new HashMap<Character, Integer>();public String minWindow(String s, String t) {Map<Character, Integer> ori = new HashMap<>();Map<Character, Integer> cnt = new HashMap<>();// 预处理,初始化 ori 表for (int i = 0; i < t.length(); i++) {char c = t.charAt(i);ori.put(c, ori.getOrDefault(c, 0) + 1);}int l = 0, r = 0;int len = Integer.MAX_VALUE, ansL = -1, ansR = -1;int sLen = s.length();int required = ori.size(); // 需要匹配的字符种类数量int formed = 0; // 已经匹配的字符种类数量while (r < sLen) {char c = s.charAt(r);cnt.put(c, cnt.getOrDefault(c, 0) + 1);if (ori.containsKey(c) && cnt.get(c).equals(ori.get(c))) {formed++;}while (formed == required && l <= r) {if (r - l + 1 < len) {len = r - l + 1;ansL = l;ansR = l + len;}char leftChar = s.charAt(l);cnt.put(leftChar, cnt.get(leftChar) - 1);if (ori.containsKey(leftChar) && cnt.get(leftChar) < ori.get(leftChar)) {formed--;}l++;}r++;}return ansL == -1 ? "" : s.substring(ansL, ansR);}注意:这里 t 中可能出现重复的字符,所以我们要记录字符的个数。
考虑如何优化? 如果 s=XX⋯XABCXXXX,t=ABC,那么显然 [XX⋯XABC]是第一个得到的「可行」区间,得到这个可行区间后,我们按照「收缩」窗口的原则更新左边界,得到最小区间。我们其实做了一些无用的操作,就是更新右边界的时候「延伸」进了很多无用的 X,更新左边界的时候「收缩」扔掉了这些无用的 X,做了这么多无用的操作,只是为了得到短短的 ABC。没错,其实在 s 中,有的字符我们是不关心的,我们只关心 t中出现的字符,我们可不可以先预处理 s,扔掉那些 t 中没有出现的字符,然后再做滑动窗口呢?也许你会说,这样可能出现 XXABXXC的情况,在统计长度的时候可以扔掉前两个 X,但是不扔掉中间的 X,怎样解决这个问题呢?优化后的时空复杂度又是多少?代码给出优化的版本.
public class MinimumWindowSubstring {public String minWindow(String s, String t) {// 用于记录 t 中各字符需要匹配的次数Map<Character, Integer> ori = new HashMap<>();// 用于记录当前窗口中各字符已匹配的次数Map<Character, Integer> cnt = new HashMap<>();// 预处理,初始化 ori 表for (int i = 0; i < t.length(); i++) {char c = t.charAt(i);ori.put(c, ori.getOrDefault(c, 0) + 1);}int l = 0, r = 0; // 窗口的左右边界int len = Integer.MAX_VALUE; // 记录当前最小窗口的长度int ansL = -1, ansR = -1; // 记录当前最小窗口的左右边界int sLen = s.length(); // 字符串 s 的长度int required = ori.size(); // 需要匹配的字符种类数量int formed = 0; // 已经匹配的字符种类数量// 右指针滑动while (r < sLen) {char c = s.charAt(r);cnt.put(c, cnt.getOrDefault(c, 0) + 1);// 如果当前字符在 ori 表中,并且已匹配次数等于 ori 表中的次数,增加已匹配字符种类数量if (ori.containsKey(c) && cnt.get(c).equals(ori.get(c))) {formed++;}// 左指针滑动,窗口收缩while (formed == required && l <= r) {// 更新最小窗口的长度和边界if (r - l + 1 < len) {len = r - l + 1;ansL = l;ansR = l + len;}// 移动左指针,减少已匹配字符的次数char leftChar = s.charAt(l);cnt.put(leftChar, cnt.get(leftChar) - 1);// 如果左边界字符在 ori 表中,并且减少后的次数小于 ori 表中的次数,减少已匹配字符种类数量if (ori.containsKey(leftChar) && cnt.get(leftChar) < ori.get(leftChar)) {formed--;}l++;}// 右指针继续滑动r++;}// 返回最小窗口对应的子串return ansL == -1 ? "" : s.substring(ansL, ansR);}
}这段代码中的核心思想是使用滑动窗口来找到包含字符串 t 中所有字符的最小窗口。下面是代码中各部分的解释:
-
ori和cnt的初始化:ori表用于记录字符串t中各字符需要匹配的次数。cnt表用于记录当前窗口中各字符已匹配的次数。
-
预处理,初始化
ori表:- 遍历字符串
t,将其中各字符及其需要匹配的次数记录在ori表中。
- 遍历字符串
-
窗口的左右边界
l和r:- 使用两个指针
l和r来确定窗口。
- 使用两个指针
-
required和formed:required记录需要匹配的字符种类数量,即ori表的大小。formed记录已经匹配的字符种类数量,初始为 0。
-
右指针滑动(
while (r < sLen)):- 不断移动右指针
r,直到窗口包含了字符串s中的所有字符。
- 不断移动右指针
-
左指针滑动,窗口收缩(
while (formed == required && l <= r)):- 移动左指针
l,尝试缩小窗口的大小。 - 更新最小窗口的长度和边界。
- 移动左指针
-
左右指针继续滑动,直至右指针到达字符串末尾:
相关文章:

76. 最小覆盖子串。优化官方题解!
leetcode原题如下: 给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。 注意: 对于 t 中重复字符,我们寻找的子字符串中该字符数量…...

在国产GPU寒武纪MLU上快速上手Pytorch使用指南
本文旨在帮助Pytorch使用者快速上手使用寒武纪MLU。以代码块为主,文字尽可能简洁,许多部分对标NVIDIA CUDA。不正确的地方请留言更正。本文不定期更新。 文章目录 前言Cambricon PyTorch的Python包torch_mlu导入将模型加载到MLU上model.to(mlu)定义损失函…...

重生奇迹MU觉醒战士攻略
剑士连招技巧:生命之光:PK前起手式,增加血上限。 雷霆裂闪:眩晕住对手,剑士PK战士第一技能,雷霆裂闪是否使用好关系到胜负。 霹雳回旋斩:雷霆裂闪后可以选择用霹雳回旋斩跑出一定范围(因为对手…...

美颜技术详解:深入了解视频美颜SDK的工作机制
本文将深入探讨视频美颜SDK的工作机制,揭示其背后的科技奥秘和算法原理。 1.引言 视频美颜SDK作为一种集成到应用程序中的技术工具,通过先进的算法和图像处理技术,为用户提供令人印象深刻的实时美颜效果。 2.视频美颜SDK的基本工作原理 首…...
3D模型格式转换工具如何实现高性能数据转换?请看CAE系统开发实例!
客户背景 DP Technology是全球知名的CAM的供应商,在全球8个国家设有18个办事处。DP Technology提供的CAMESPRIT系统是一个用于数控编程,优化和仿真全方面的CAM系统。CAMESPRIT的客户来自多个行业,因此支持多种CAD工具和文件格式显得格外重…...
多级缓存:亿级流量的缓存方案
文章目录 一.多级缓存的引入二.JVM进程缓存三.Lua语法入门四.多级缓存1.OpenResty2.查询Tomcat3.Redis缓存预热4.查询Redis缓存5.Nginx本地缓存6.缓存同步 一.多级缓存的引入 传统缓存的问题 传统的缓存策略一般是请求到达Tomcat后,先查询Redis,如果未…...
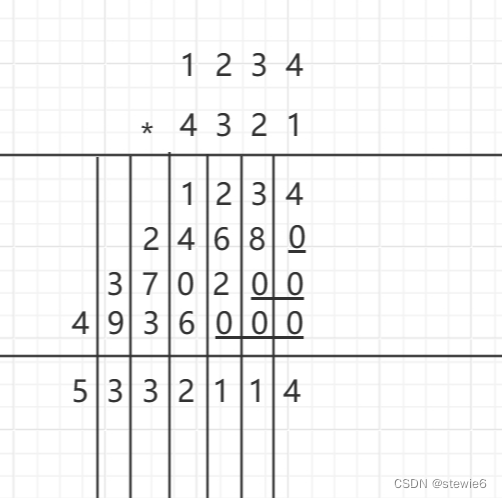
C语言——高精度乘法
一、引子 高精度乘法相较于高精度加法和减法有更多的不同,加法和减法是一位对应一位进行操作的,而乘法是一个数的每一位对另一个数的每一位进行操作,需要的计算步骤更多。 二、核心算法 void Calculate(int num1[], int num2[], int numres…...
为什么C语言没有被C++所取代呢?
今日话题,为什么C语言没有被C所取代呢?虽然C是一个功能更强大的语言,但C语言在嵌入式领域仍然广泛使用,因为它更轻量级、更具可移植性,并且更适合在资源受限的环境中工作。这就是为什么C语言没有被C所取代的原因。如果…...
)
基于Spring的枚举类+策略模式设计(以实现多种第三方支付功能为例)
摘要 最近阅读《贯彻设计模式》这本书,里面使用一个更真实的项目来介绍设计模式的使用,相较于其它那些只会以披萨、厨师为例的设计模式书籍是有些进步。但这书有时候为了使用设计模式而强行朝着对应的 UML 图来设计类结构,并且对设计理念缺少…...

基于Linphone android sdk开发Android软话机
1.Linphone简介 1.1 简介 LinPhone是一个遵循GPL协议的开源网络电话或者IP语音电话(VOIP)系统,其主要如下。使用linphone,开发者可以在互联网上随意的通信,包括语音、视频、即时文本消息。linphone使用SIP协议&#…...
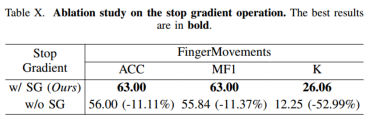
[论文分享]TimeDRL:多元时间序列的解纠缠表示学习
论文题目:TimeDRL: Disentangled Representation Learning for Multivariate Time-Series 论文地址:https://arxiv.org/abs/2312.04142 代码地址:暂无 关键要点:多元时间序列,自监督表征学习,分类和预测 摘…...
分享一个好看的vs主题
最近发现了一个很好看的vs主题(个人认为挺好看的),想要分享给大家。 主题的名字叫NightOwl,和vscode的主题颜色挺像的。操作方法也十分简单,首先我们先在最上面哪一行找到扩展。 然后点击管理扩展,再搜索栏…...

什么是云呼叫中心?
云呼叫中心作为一种高效的企业呼叫管理方案,越来越受到企业的青睐,常被用于管理客服和销售业务。那么,云呼叫中心到底是什么? 什么是云呼叫中心? 云呼叫中心是一种基于互联网的呼叫管理系统,与传统的呼叫…...
还在用nvm?来试试更快的node版本管理工具——fnm
前言 📫 大家好,我是南木元元,热衷分享有趣实用的文章,希望大家多多支持,一起进步! 🍅 个人主页:南木元元 目录 什么是node版本管理 常见的node版本管理工具 fnm是什么 安装fnm …...
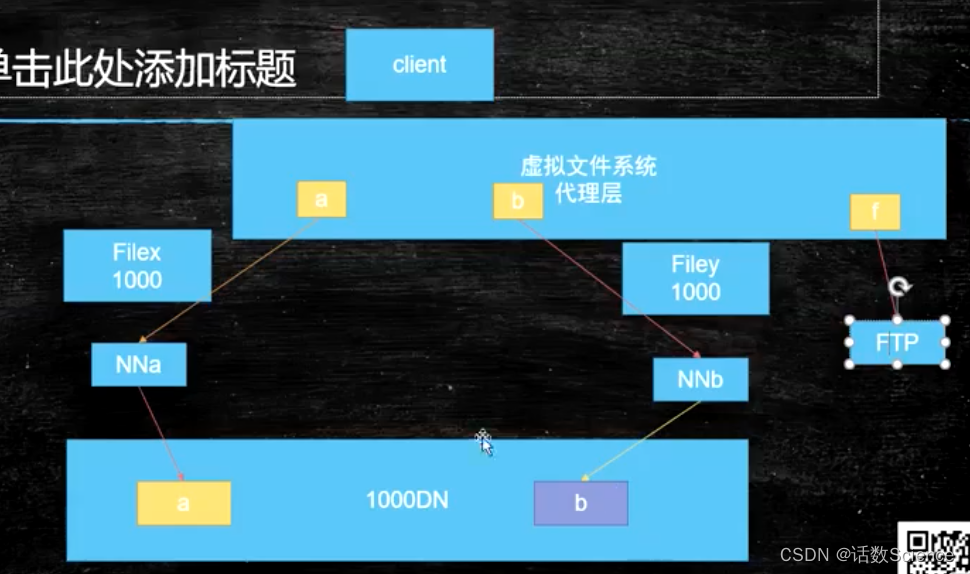
【Hadoop精讲】HDFS详解
目录 理论知识点 角色功能 元数据持久化 安全模式 SecondaryNameNode(SNN) 副本放置策略 HDFS写流程 HDFS读流程 HA高可用 CPA原则 Paxos算法 HA解决方案 HDFS-Fedration解决方案(联邦机制) 理论知识点 角色功能 元数据持久化 另一台机器就…...
企业需要哪些数字化管理系统?
企业需要哪些数字化管理系统? ✅企业引进管理系统肯定是为了帮助整合和管理大量的数据,从而优化业务流程,提高工作效率和生产力。 ❌但是,如果各个系统之间不互通、无法互相关联数据的话,反而会增加工作量和时间成本…...
【vue】开发常见问题及解决方案
有一些问题不限于 Vue,还适应于其他类型的 SPA 项目。 1. 页面权限控制和登陆验证页面权限控制 页面权限控制是什么意思呢? 就是一个网站有不同的角色,比如管理员和普通用户,要求不同的角色能访问的页面是不一样的。如果一个页…...

飞天使-k8s知识点3-卸载yum 安装的k8s
要彻底卸载使用yum安装的 Kubernetes 集群,您可以按照以下步骤进行操作: 停止 Kubernetes 服务: sudo systemctl stop kubelet sudo systemctl stop docker 卸载 Kubernetes 组件: sudo yum remove -y kubelet kubeadm kubectl…...

ZooKeeper 集群搭建
文章目录 ZooKeeper 概述选举机制搭建前准备分布式配置分布式安装解压缩并重命名配置环境配置服务器编号配置文件 操作集群编写脚本运行脚本搭建过程中常见错误 ZooKeeper 概述 Zookeeper 是一个开源的分布式服务协调框架,由Apache软件基金会开发和维护。以下是对Z…...

Meson:现代的构建系统
Meson是一款现代化、高性能的开源构建系统,旨在提供简单、快速和可读性强的构建脚本。Meson被设计为跨平台的,支持多种编程语言,包括C、C、Fortran、Python等。其目标是替代传统的构建工具,如Autotools和CMake,提供更简…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...
