【生物信息学】层次聚类过程
文章目录
- 一、理论
- 二、实践
- 过程1
- 过程2
一、理论
层次聚类是一种基于树状结构的聚类方法,它试图通过在不同层次上逐步合并或分裂数据集来构建聚类结构。这个树状结构通常被称为“树状图”(dendrogram),其中每个节点代表一个数据点或一组数据点,而连接节点的分支表示聚类的形成过程。
下面是层次聚类的一般原理:
-
距离矩阵计算: 首先,计算数据集中每对数据点之间的距离。这可以是欧氏距离、曼哈顿距离、相关性等不同的距离度量。
-
初始化: 将每个数据点作为一个独立的簇,形成初始的聚类。
-
迭代合并或分裂: 从最小距离开始,迭代地合并或分裂簇,直到满足某个停止条件。
-
合并(Agglomerative): 从底层开始,将最近的两个簇合并为一个新的簇。合并的标准可以是簇内点之间的最小距离、最大距离、平均距离等。
-
分裂(Divisive): 从顶层开始,将一个簇分裂成两个新的簇。分裂的标准通常是选择一个簇中的一个点,然后将其他点分配给最近的簇。
-
-
更新距离矩阵: 在每次合并或分裂后,更新距离矩阵,反映新形成的簇之间的距离。
-
形成树状图: 记录每次合并或分裂的过程,形成树状图。树状图的叶子节点代表单个数据点,内部节点代表合并的簇。
-
停止条件: 根据具体任务和目标选择停止合并或分裂的条件,可以是簇的数量、簇的直径、距离的阈值等。
层次聚类的优点之一是它提供了在不同层次上观察数据结构的能力,同时不需要预先指定簇的数量。然而,由于其复杂度较高,对大型数据集的处理可能会受到计算资源的限制。
二、实践
考虑下图所示的单链聚类,其中数据集包含 5 个点,任意两点之间的距离在图的左下角给出。绘制其按照Mini-Distance树状图
| δ \delta δ | B | C | D | E |
|---|---|---|---|---|
| A | 1 | 3 | 2 | 4 |
| B | 3 | 2 | 3 | |
| C | 1 | 3 | ||
| D | 5 |
聚类过程:
用 δ ( A , B ) \delta(A, B) δ(A,B) 表示两个簇 A 和 B 之间的距离,这个距离可以根据不同的标准进行计算,比如最小距离、最大距离、平均距离等。
过程1
这里 δ ( A , B ) = 1 , δ ( C , D ) = 1 \delta(A,B)=1,\delta(C,D)=1 δ(A,B)=1,δ(C,D)=1,选择先合并AB,则 δ ( A B , E ) = min ( δ ( A , E ) , δ ( B , E ) ) = 3 \delta(AB,E)=\min(\delta(A,E),\delta(B,E))=3 δ(AB,E)=min(δ(A,E),δ(B,E))=3
| δ \delta δ | C | D | E |
|---|---|---|---|
| AB | 3 | 2 | 3 |
| C | 1 | 3 | |
| D | 5 |
- 再合并CD,则
| δ \delta δ | CD | E |
|---|---|---|
| AB | 2 | 3 |
| CD | 3 |
- 再合并ABCD,则
| δ \delta δ | E |
|---|---|
| ABCD | 3 |
┌──────── ABCDE ────────┐│3 │┌──── ABCD ────┐ ││2 2│ 3│
┌───── AB ────┐ ┌──── CD ───┐ │
│1 1│ │1 │1 │
A B C D E
过程2
- 选择先合并CD
| δ \delta δ | B | C | D | E |
|---|---|---|---|---|
| A | 1 | 3 | 2 | 4 |
| B | 3 | 2 | 3 | |
| C | 1 | 3 | ||
| D | 5 |
- δ ( C D , E ) = min ( δ ( C , E ) , δ ( D , E ) ) = 3 \delta(CD,E)=\min(\delta(C,E),\delta(D,E))=3 δ(CD,E)=min(δ(C,E),δ(D,E))=3
- δ ( C D , A ) = min ( δ ( C , A ) , δ ( D , A ) ) = 2 \delta(CD,A)=\min(\delta(C,A),\delta(D,A))=2 δ(CD,A)=min(δ(C,A),δ(D,A))=2
- δ ( C D , B ) = min ( δ ( C , B ) , δ ( D , B ) ) = 2 \delta(CD,B)=\min(\delta(C,B),\delta(D,B))=2 δ(CD,B)=min(δ(C,B),δ(D,B))=2
| δ \delta δ | B | CD | E |
|---|---|---|---|
| A | 1 | 2 | 4 |
| B | 2 | 3 | |
| CD | 3 |
-
再合并AB
-
δ ( A B , C D ) = min ( δ ( A , C D ) , δ ( B , C D ) ) = 2 \delta(AB,CD)=\min(\delta(A,CD),\delta(B,CD))=2 δ(AB,CD)=min(δ(A,CD),δ(B,CD))=2
-
δ ( A B , E ) = min ( δ ( A , E ) , δ ( B , E ) ) = 3 \delta(AB,E)=\min(\delta(A,E),\delta(B,E))=3 δ(AB,E)=min(δ(A,E),δ(B,E))=3
| δ \delta δ | CD | E |
|---|---|---|
| AB | 2 | 3 |
| CD | 3 |
- 再合并ABCD,则
| δ \delta δ | E |
|---|---|
| ABCD | 3 |
相关文章:

【生物信息学】层次聚类过程
文章目录 一、理论二、实践过程1过程2 一、理论 层次聚类是一种基于树状结构的聚类方法,它试图通过在不同层次上逐步合并或分裂数据集来构建聚类结构。这个树状结构通常被称为“树状图”(dendrogram),其中每个节点代表一个数据点或…...

变分自动编码器【03/3】:使用 Docker 和 Bash 脚本进行超参数调整
一、说明 在深入研究第 1 部分中的介绍和实现,并在第 2 部分中探索训练过程之后,我们现在将重点转向在第 3 部分中通过超参数调整来优化模型的性能。要访问本系列的完整代码,请访问我们的 GitHub 存储库在GitHub - asokraju/ImageAutoEncoder…...
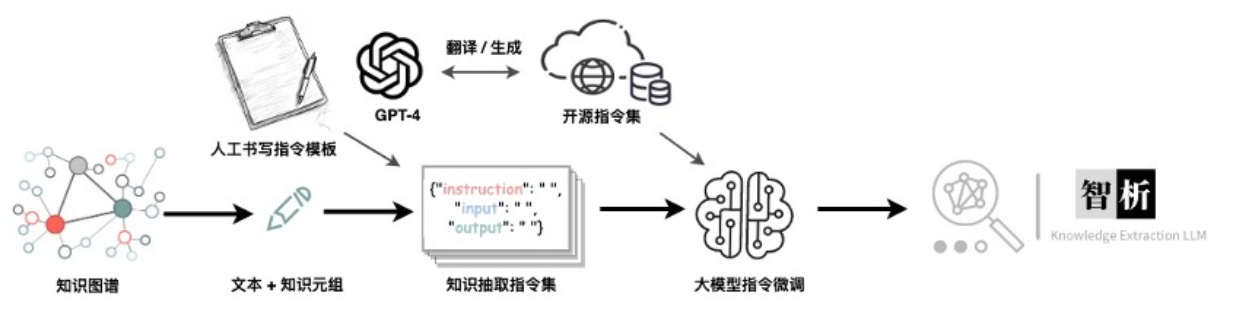
KnowLM知识抽取大模型
文章目录 KnowLM项目介绍KnowLM项目的动机ChatGPT存在的问题 基于LLama的知识抽取的智析大模型数据集构建及训练过程预训练数据集构建预训练训练过程指令微调数据集构建 指令微调训练过程开源的数据集及模型局限性信息抽取Prompt 部署环境配置模型下载预训练模型使用LoRA模型使…...
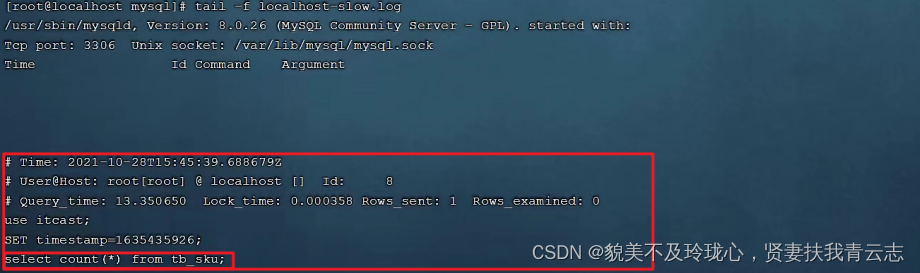
MySQL数据库 索引
目录 索引概述 索引结构 二叉树 B-Tree BTree Hash 索引分类 索引语法 慢查询日志 索引概述 索引 (index)是帮助MySQL高效获取数据的数据结构(有序)。在数据之外,数据库系统还维护着满足特定查找算法的数据结构,这些数据结构以某种…...

ES 错误码
2xx状态码(如200)表示请求成功处理,并且不需要重试。 400状态码表示客户端发送了无效的请求,例如请求的语法有误或缺少必需的参数。在这种情况下,重试相同的请求很可能会导致相同的错误。因此,应该先检查并…...

听GPT 讲Rust源代码--src/tools(18)
File: rust/src/tools/rust-analyzer/crates/ide-ssr/src/from_comment.rs 在Rust源代码中的from_comment.rs文件位于Rust分析器(rust-analyzer)工具的ide-ssr库中,它的作用是将注释转换为Rust代码。 具体来说,该文件实现了从注…...

如何实现设备远程控制?
在工业自动化领域,设备远程控制是一项非常重要的技术。它使得设备可以在远离现场的情况下进行远程操作和维护,大大提高了设备的可用性和效率。 设备远程控制的应用场景有哪些? 远程故障排除:当设备出现故障时,工程师…...

百度侯震宇详解:大模型将如何重构云计算?
12月20日,在2023百度云智大会智算大会上,百度集团副总裁侯震宇以“大模型重构云计算”为主题发表演讲。他强调,AI原生时代,面向大模型的基础设施体系需要全面重构,为构建繁荣的AI原生生态筑牢底座。 侯震宇表示&…...

[Java]FileOutputStream的换行/续写/一次性写出一个字符串的方法
1.续写:FileOutputStream这个io流中的write方法默认情况下是覆盖写入的,如果需要追加写入,需要添加一个参数true 2.虽然write只能一个字符一个字符写入 但是我们可以把想输入的字符串放在str 再将str转化成byte数组 import java.io.FileOutp…...

VM进行TCP/IP通信
OK就变成这样 vm充当服务端的话也是差不多的操作 点击连接 这里我把端口号换掉了因为可能被占用报错了,如果有报错可以尝试尝试换个端口号 注: 还有一个点在工作中要是充当服务器,要去网络这边看下他的ip地址 拉到最后面...

剑指Offer 队列栈题目集合
目录 用两个栈实现队列 用两个栈实现队列 刷题链接: https://www.nowcoder.com/practice/54275ddae22f475981afa2244dd448c6 题目描述 思路一: 使用两个栈来实现队列的功能。栈 1 用于存储入队的元素,而栈 2 用于存储出队的元素。 1.push…...

grafana基本使用
一、安装grafana 1.下载 官网下载地址: https://grafana.com/grafana/download官网包的下载地址: yum install -y https://dl.grafana.com/enterprise/release/grafana-enterprise-10.2.2-1.x86_64.rpm官网下载速度非常慢,这里选择清华大…...
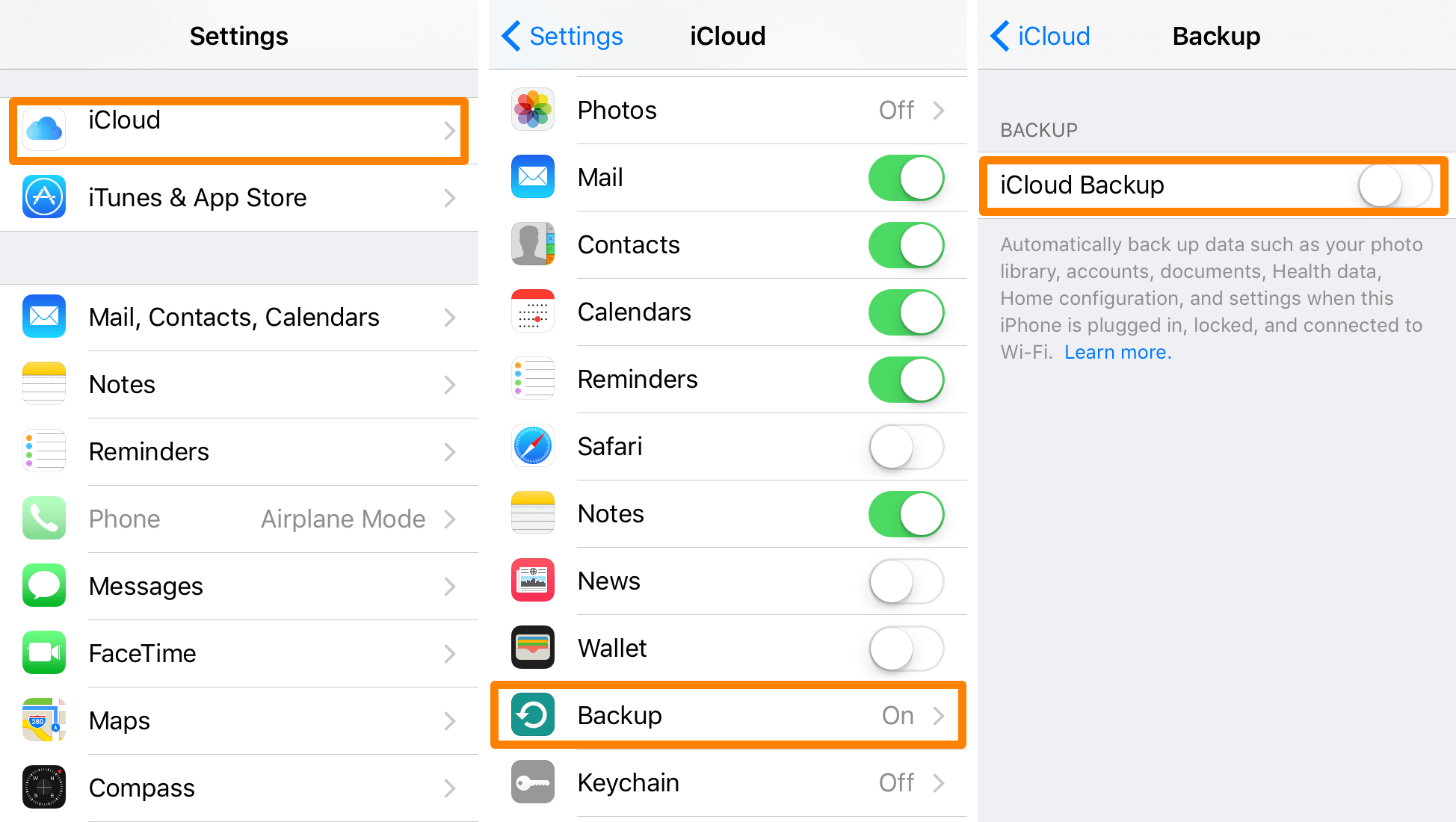
备份至关重要!如何解决iCloud的上次备份无法完成的问题
将iPhone和iPad备份到iCloud对于在设备发生故障或丢失时确保数据安全至关重要。但iOS用户有时会收到一条令人不安的消息,“上次备份无法完成。”下面我们来看看可能导致此问题的原因,如何解决此问题,并使你的iCloud备份再次顺利运行。 这些故…...

【项目问题解决】% sql注入问题
目录 【项目问题解决】% sql注入问题 1.问题描述2.问题原因3.解决思路4.解决方案1.前端限制传入特殊字符2.后端拦截特殊字符-正则表达式3.后端拦截特殊字符-拦截器 5.总结6.参考 文章所属专区 项目问题解决 1.问题描述 在处理接口入参的一些sql注入问题,虽然通过M…...
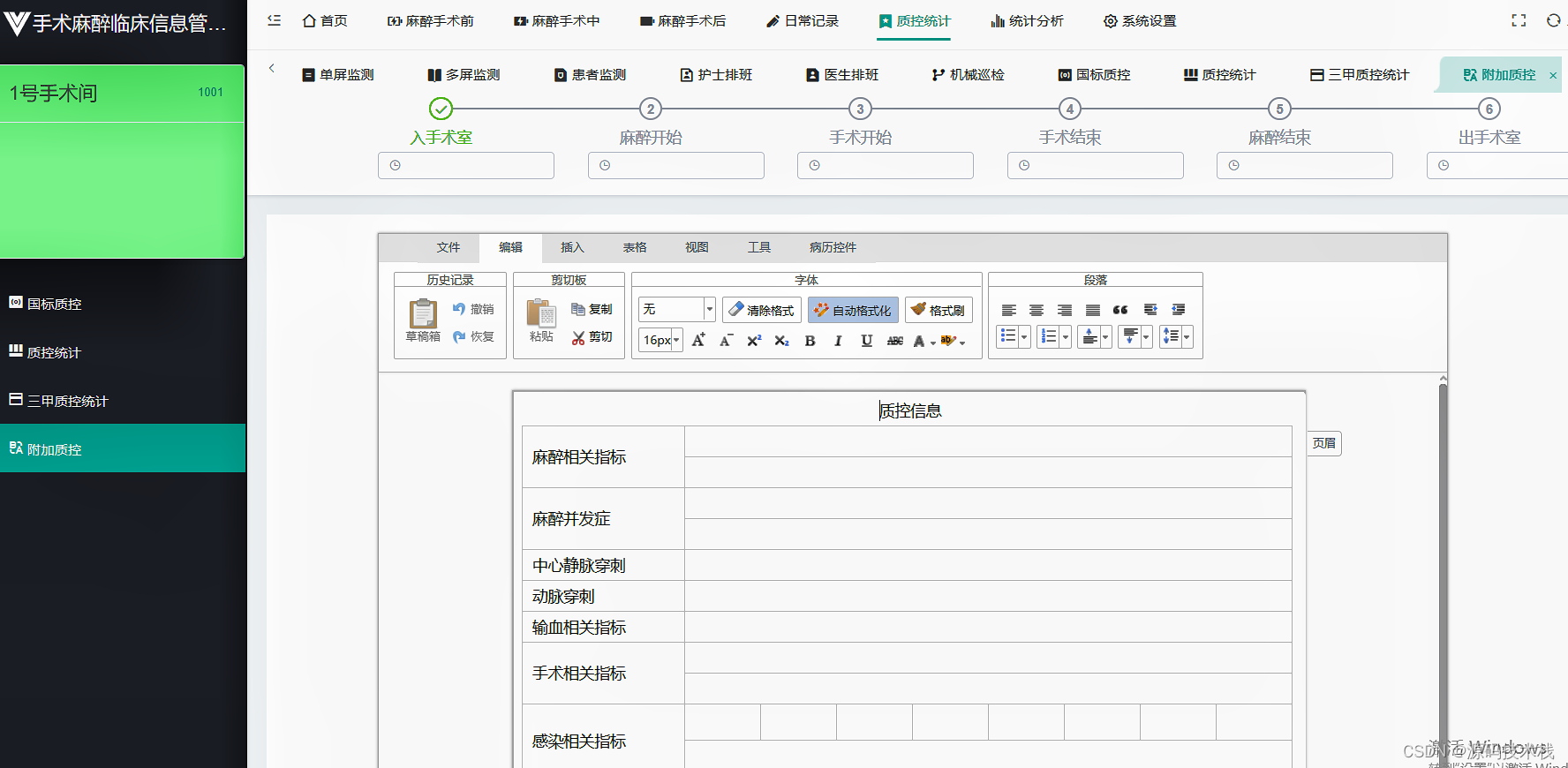
B/S医院手术麻醉临床管理系统源码 手术申请、手术安排
手术麻醉系统概述 手术室是医院各个科室工作交叉汇集的一个重要中心,在时间、空间、设备、药物、材料、人员调配的科学管理、高效运作、安全质控、绩效考核,都十分重要。手术麻醉管理系统(Operation Anesthesia Management System࿰…...

解锁高效工作!5款优秀工时管理软件推荐
工时管理,一直是让许多企业和团队头疼的问题。传统的纸质工时表、复杂的电子表格,不仅操作繁琐,还容易出错。幸好,随着科技的进步,我们迎来了工时管理软件的春天。今天,就让我们一起走进这个新时代…...

ICLR 2024 高分论文 | Step-Back Prompting 使大语言模型通过抽象进行推理
文章目录 一、前言二、主要内容三、总结🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 一、前言 ICLR 2024 高分论文:《Step-Back Prompting Enables Reasoning Via Abstraction in Large Language Models》 论文地址:https://openreview.net/forum?id=3bq3jsvcQ1 …...
边缘计算有哪些常用场景?TSINGSEE边缘AI视频分析技术行业解决方案
随着ChatGPT生成式人工智能的爆发,AI技术在业界又掀起一波新浪潮。值得关注的是,边缘AI智能也在AI人工智能技术进步的基础上得到了快速发展。IDC跟踪报告数据显示,2021年我国的边缘计算服务器整体市场规模达到33.1亿美元,预计2020…...

配置BGP的基本示例
目录 BGP简介 BGP定义 配置BGP目的 受益 实验 实验拓扑 编辑 组网需求 配置思路 配置步骤 配置各接口所属的VLAN 配置各Vlanif的ip地址 配置IBGP连接 配置EBGP 查看BGP对等体的连接状态 配置SwitchA发布路由10.1.0.0/16 配置BGP引入直连路由 BGP简介 BGP定义 …...
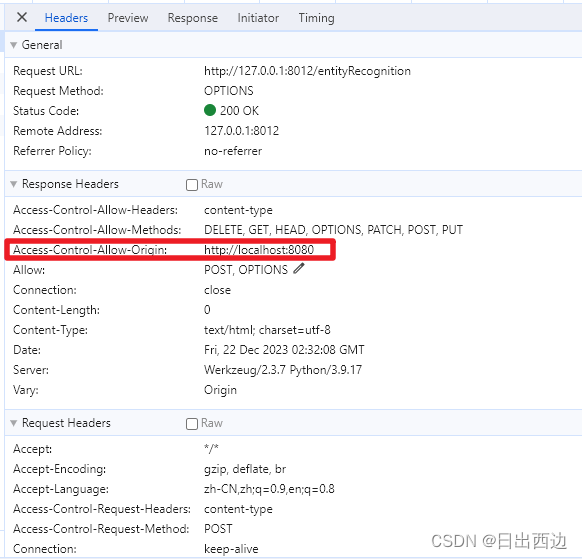
Flask解决接口跨域问题
1、什么是跨域CROS CORS(Cross-Origin Resource Sharing,跨域资源共享)是一种浏览器安全策略,用于控制在一个网页应用中如何让一个域的Web页面能够请求另一个域的资源。在Web开发中,由于同源策略(Same-Ori…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...

2025年低延迟业务DDoS防护全攻略:高可用架构与实战方案
一、延迟敏感行业面临的DDoS攻击新挑战 2025年,金融交易、实时竞技游戏、工业物联网等低延迟业务成为DDoS攻击的首要目标。攻击呈现三大特征: AI驱动的自适应攻击:攻击流量模拟真实用户行为,差异率低至0.5%,传统规则引…...

医疗AI模型可解释性编程研究:基于SHAP、LIME与Anchor
1 医疗树模型与可解释人工智能基础 医疗领域的人工智能应用正迅速从理论研究转向临床实践,在这一过程中,模型可解释性已成为确保AI系统被医疗专业人员接受和信任的关键因素。基于树模型的集成算法(如RandomForest、XGBoost、LightGBM)因其卓越的预测性能和相对良好的解释性…...
