【动画图解】一次理清九大排序算法!面试官问到再也不慌!
排序算法
- 交换排序
- 冒泡排序
- 快速排序
- 插入排序
- 直接插入排序
- 希尔排序
- 选择排序
- 简单选择排序
- 堆排序
- 归并排序
- 基数排序
- 桶排序
一、冒泡排序
冒泡排序是一种简单的交换排序算法,以升序排序为例,其核心思想是:
- 从第一个元素开始,比较相邻的两个元素。如果第一个比第二个大,则进行交换。
- 轮到下一组相邻元素,执行同样的比较操作,再找下一组,直到没有相邻元素可比较为止,此时最后的元素应是最大的数。
- 除了每次排序得到的最后一个元素,对剩余元素重复以上步骤,直到没有任何一对元素需要比较为止。
/*** 冒泡排序** @param arr*/
public void bubbleSort(int[] arr) {int tmp;// 冒泡优化:如果在某一次冒泡过程中,没有发生交换,则证明数组已经是有序的了for (int i = 0; i < arr.length; i++) {boolean flag = true;for (int j = i + 1; j < arr.length; j++) {if (arr[j] < arr[i]) {flag = false;tmp = arr[j];arr[j] = arr[i];arr[i] = tmp;}}if (flag) {break;}}
}
二、快速排序
快速排序的思想很简单,就是先把待排序的数组拆成左右两个区间,左边都比中间的基准数小,右边都比基准数大。接着左右两边各自再做同样的操作,完成后再拆分再继续,一直到各区间只有一个数为止。
/*** 快速排序** @param arr*/
public void quickSort(int[] arr, int low, int high) {if (low >= high) {return;}int left = low;int right = high;int baseIndex = left;int base = arr[baseIndex];int tmp;while (left < right) {while (arr[right] >= base && left < right) {// 以base为基准,从右往左找到比基准小的数right--;}while (arr[left] <= base && left < right) {// 以base为基准,从左往右找到比基准大的数left++;}if (left < right) {// 左右还没相交,大小对换位置tmp = arr[left];arr[left] = arr[right];arr[right] = tmp;}}// 这一轮快排结束,交换相遇点与基准点,把基准数放在对应的位置上// 因为要把基准数和相遇点交换,由于if判断包含等于,那么从左往右就会找到比基准数小的数,从右往左就会找到比基准数大的数,会越过基准数// 因此当基准点小于相遇点时(基准点取第一位数),必须保证从先移动右指针,再移动左指针;当基准点大于相遇点时(基准点取最后一位位数),必须保证从先移动左指针,再移动右指针// 如果一定要随机基准数,有个简单的改进方法,就是随机一位数,与首位,或最后一位先做一下交换tmp = arr[baseIndex];arr[baseIndex] = arr[right];arr[right] = tmp;//数组“分两半”,再重复上面的操作quickSort(arr, low, left - 1);quickSort(arr, left + 1, high);
}
三、插入排序
插入排序是一种简单的排序方法,其基本思想是将一个记录插入到已经排好序的有序表中,使得被插入数的序列同样是有序的。按照此法对所有元素进行插入,直到整个序列排为有序的过程。
1. 直接插入排序
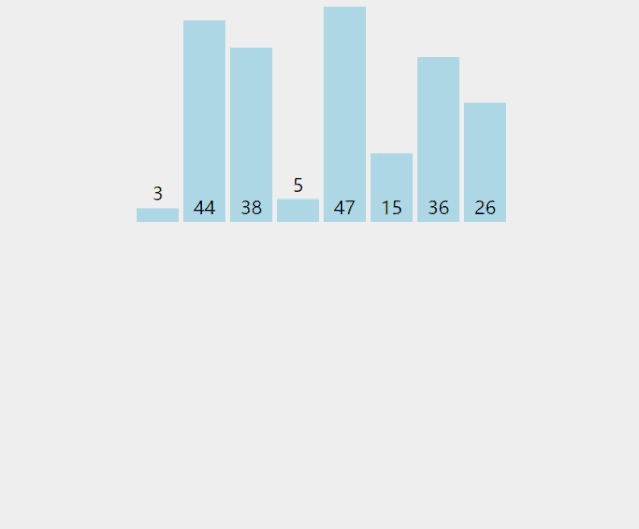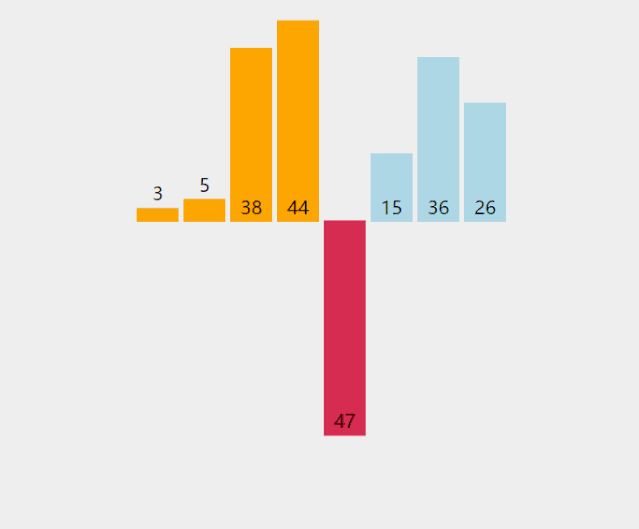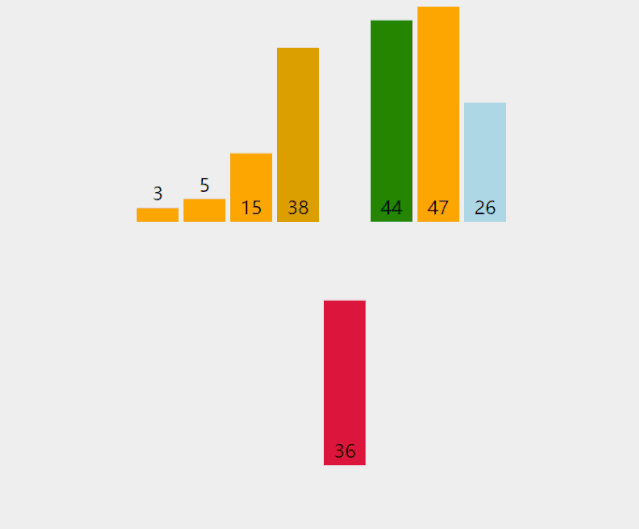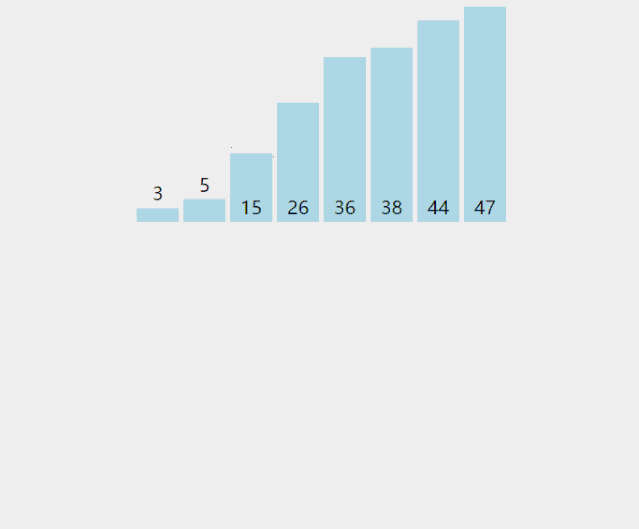
直接插入排序就是插入排序的粗暴实现。对于一个序列,选定一个下标,认为在这个下标之前的元素都是有序的。将下标所在的元素插入到其之前的序列中。接着再选取这个下标的后一个元素,继续重复操作。直到最后一个元素完成插入为止。我们一般从序列的第二个元素开始操作。
/*** 插入排序** @param arr*/
public void insertSort(int[] arr) {// 从第二个数开始遍历for (int i = 1; i < arr.length; i++) {// 插入的数int insertNum = arr[i];// 寻找插入点int insertIndex = 0;for (int j = 0; j < i; j++, insertIndex++) {// 插入点在比插入数大的这一位的前面if (insertNum < arr[j]) {break;}}// 从插入点往后依次挪动for (int j = i; j >= insertIndex; j--) {if (j > 0) {arr[j] = arr[j - 1];}}// 最后插入数据arr[insertIndex] = insertNum;}
}
插入排序对已经排好序的数组操作时,效率很高
2. 希尔排序
某些情况下直接插入排序的效率极低。比如一个已经有序的升序数组,这时再插入一个比最小值还要小的数,也就意味着被插入的数要和数组所有元素比较一次。我们需要对直接插入排序进行改进。
我们可以试着先将数组变为一个相对有序的数组,然后再做插入排序。
希尔排序的步骤简述如下:
- 把元素按步长gap分组,gap的数值其实就是分组的个数。gap的起始值为数列长度的一半,每循环一轮gap减为原来的一半。
- 对每组元素采用直接插入排序算法进行排序。
- 随着步长逐渐减小,组就越少,组中包含的元素就越多。
- 当步长值减小到1时,整个数据合成一组,最后再对这一组数列用直接插入排序进行最后的调整,最终完成排序。
我们以无序数列[5,8,6,3,9,2,1,7,,4]为例,详细介绍希尔排序的步骤:
(1). 第一轮排序,gap = length/2 = 4,即将数组分成4组。四组元素分别为[5,9,4]、[8,2]、[6,1]、[3,,7]。对四组元素分别进行排序结果为:[4,5,9]、[2,8]、[1,6]、[3,7]。将四组排序结果进行合并,得到第一轮的排序结果为:[4,2,1,3,5,8,6,7,9]。如下图所示。
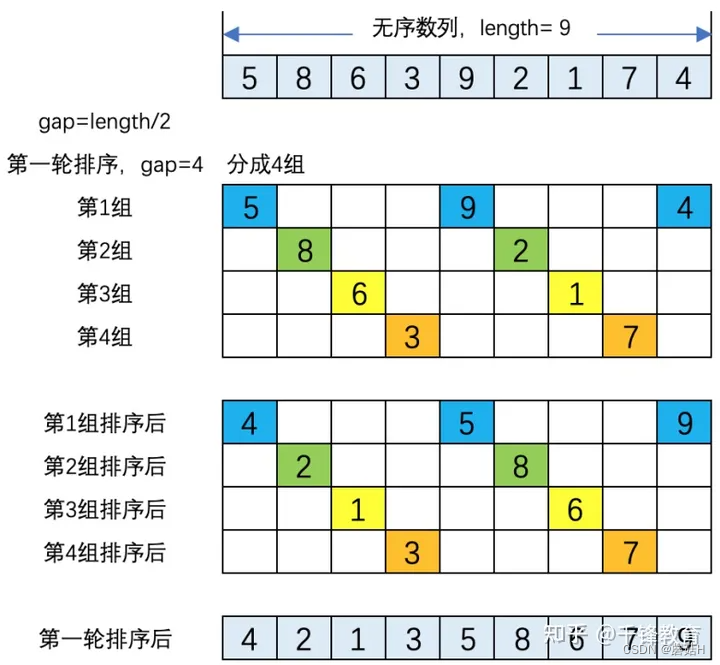
(2). 第二轮排序,gap = 2,将数列分成2组。两组的元素分别是[4,1,5,6,9]和[2,3,8,,7]。这两个组分别执行直接插入排序后的结果为[1,4,5,6,9]和[2,3,7,8]。将两组合并后的结果为[1,2,4,3,5,7,6,8,9],如下图所示。
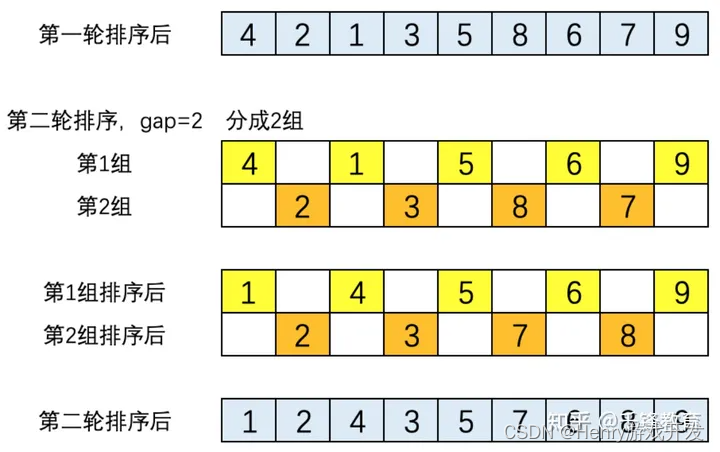
(3). 第三轮排序,gap = 1,数组就变成了一组。该组的元素是[1,2,4,3,5,7,6,8,9],这个组执行直接插入排序后结果为[1,2,3,4,5,6,7,8,9],这个结果就是第三轮排序后得到的结果。此时排序完成,如下图所示。
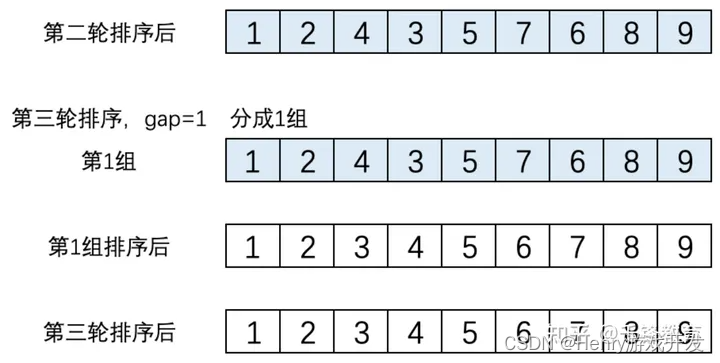
public void shellSort(int[] arr) {// gap 为步长,每次减为原来的一半。for (int gap = arr.length / 2; gap > 0; gap /= 2) {// 对每一组都执行直接插入排序for (int i = 0 ;i < gap; i++) {// 对本组数据执行直接插入排序for (int j = i + gap; j < arr.length; j += gap) {// 如果 a[j] < a[j-gap],则寻找 a[j] 位置,并将后面数据的位置都后移if (arr[j] < arr[j - gap]) {int k;int temp = arr[j];for (k = j - gap; k >= 0 && arr[k] > temp; k -= gap) {arr[k + gap] = arr[k];}arr[k + gap] = temp;}}}}
}
四、选择排序
1. 简单选择排序
选择排序思想的暴力实现,每一趟从未排序的区间找到一个最小元素,并放到第一位,直到全部区间有序为止。
public void selectSort(int[] arr) {for (int i = 0; i < arr.length; i++) {// 遍历数据int minIndex = i;for (int j = i + 1; j < arr.length; j++) {// 从当前位置往后遍历,找到最小数的下标if (arr[j] < arr[minIndex]) {minIndex = j;}}// 最小数的下标不是第一个数,那么就把最小下标和第一个数做交换if (i != minIndex) {int temp = arr[i];arr[i] = arr[minIndex];arr[minIndex] = temp;}}
}
2. 堆排序
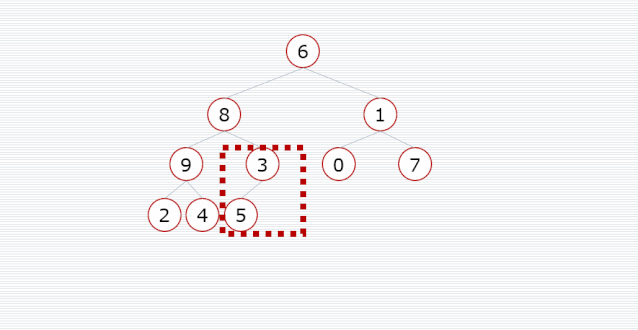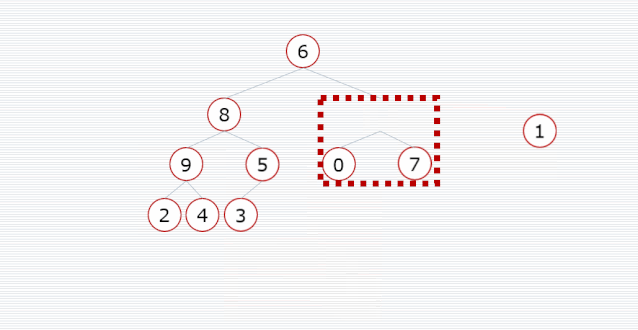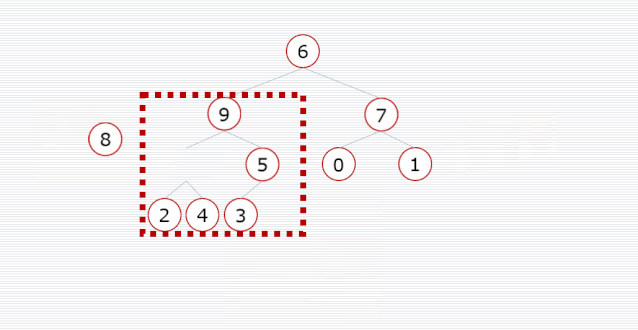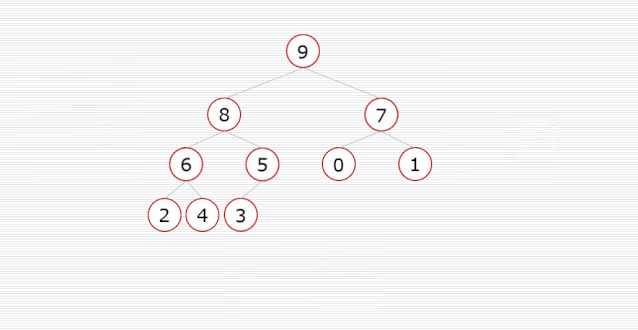
对于任何一个数组都可以看成一颗完全二叉树。堆是具有以下性质的完全二叉树
- 大顶堆:每个结点的值都大于或等于其左右孩子结点的值
- 小顶堆:每个结点的值都小于或等于其左右孩子结点的值
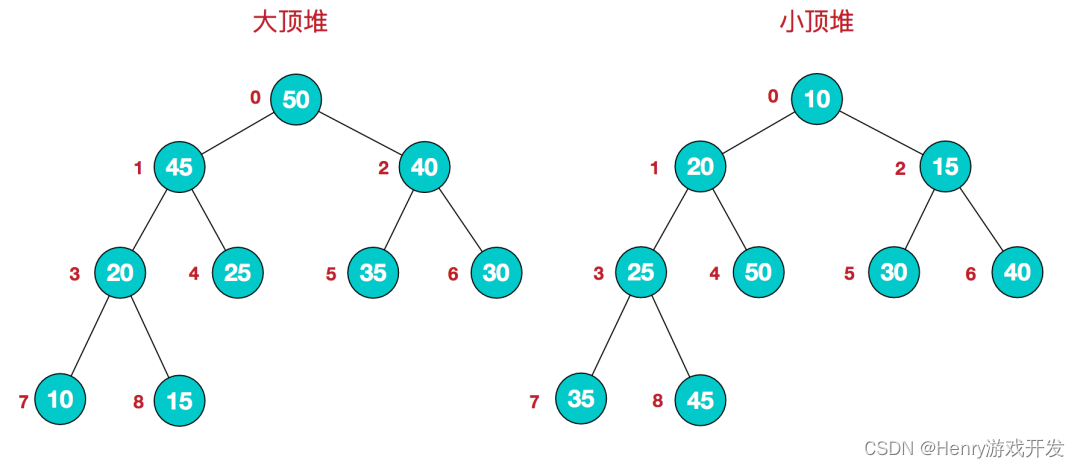
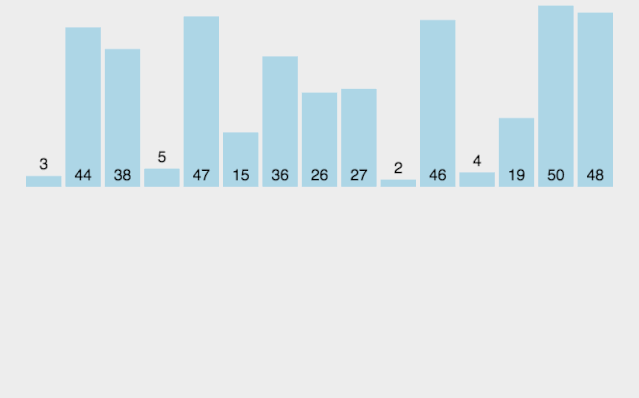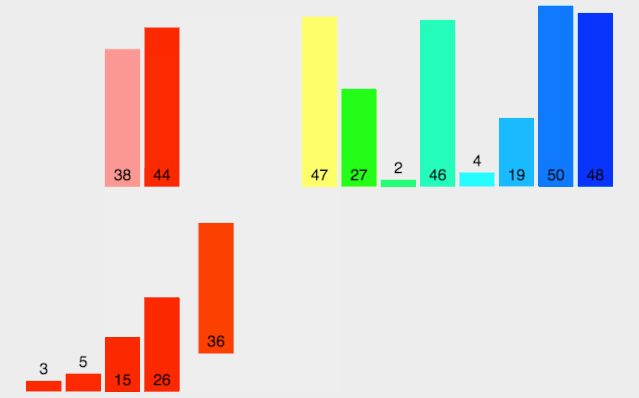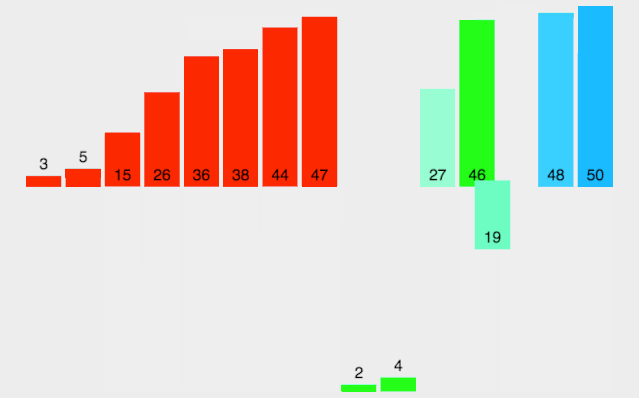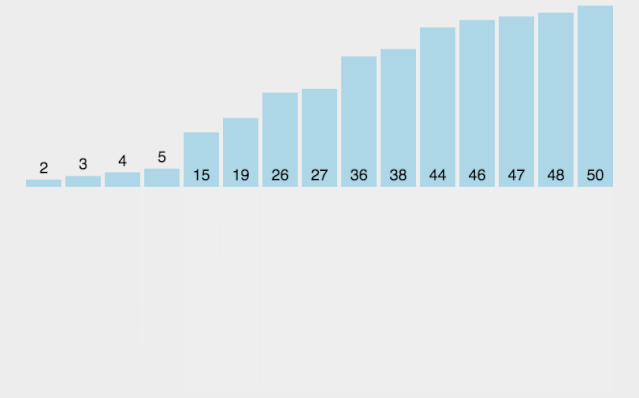
像上图的大顶堆,映射为数组,就是 [50, 45, 40, 20, 25, 35, 30, 10, 15]。可以发现第一个下标的元素就是最大值,将其与末尾元素交换,则末尾元素就是最大值。所以堆排序的思想可以归纳为以下两步:
- 将待排序的数组初始化为大顶堆,该过程即建堆。
- 将堆顶元素与最后一个元素进行交换,除去最后一个元素外可以组建为一个新的大顶堆。
- 由于第二部堆顶元素跟最后一个元素交换后,新建立的堆不是大顶堆,需要重新建立大顶堆。重复上面的处理流程,直到堆中仅剩下一个元素。
重复以上两个步骤,直到没有元素可操作,就完成排序了。
我们需要把一个普通数组转换为大顶堆,调整的起始点是最后一个非叶子结点,然后从左至右,从下至上,继续调整其他非叶子结点,直到根结点为止。
/*** 堆排序** @param arr*/
public void heapSort(int[] arr) {// 开始位置是最后一个非叶子结点,即最后一个结点的父结点int start = (arr.length - 1) / 2;// 调整为大顶堆for (int i = start; i >= 0; i--) {maxHeap(arr, arr.length, i);}// 先把数组中第 0 个位置的数和堆中最后一个数交换位置,再把前面的处理为大顶堆for (int i = arr.length - 1; i > 0; i--) {int temp = arr[0];arr[0] = arr[i];arr[i] = temp;maxHeap(arr, i, 0);}
}
/*** 转化为大顶堆** @param arr 待转化的数组* @param size 待调整的区间长度* @param index 结点下标*/
public void maxHeap(int[] arr, int size, int index) {// 左子结点int leftNode = 2 * index + 1;// 右子结点int rightNode = 2 * index + 2;int max = index;// 和两个子结点分别对比,找出最大的结点if (leftNode < size && arr[leftNode] > arr[max]) {max = leftNode;}if (rightNode < size && arr[rightNode] > arr[max]) {max = rightNode;}// 交换位置if (max != index) {int temp = arr[index];arr[index] = arr[max];arr[max] = temp;// 因为交换位置后有可能使子树不满足大顶堆条件,所以要对子树进行调整maxHeap(arr, size, max);}
}
五、归并排序
归并排序是建立在归并操作上的一种有效,稳定的排序算法。该算法采用分治法的思想,是一个非常典型的应用。归并排序的思路如下:
- 将 n 个元素分成两个各含 n/2 个元素的子序列
- 借助递归,两个子序列分别继续进行第一步操作,直到不可再分为止
- 此时每一层递归都有两个子序列,再将其合并,作为一个有序的子序列返回上一层,再继续合并,全部完成之后得到的就是一个有序的序列
关键在于两个子序列应该如何合并。假设两个子序列各自都是有序的,那么合并步骤就是:
- 创建一个用于存放结果的临时数组,其长度是两个子序列合并后的长度
- 设定两个指针,最初位置分别为两个已经排序序列的起始位置
- 比较两个指针所指向的元素,选择相对小的元素放入临时数组,并移动指针到下一位置
- 重复步骤 3 直到某一指针达到序列尾
- 将另一序列剩下的所有元素直接复制到合并序列尾
/*** 合并数组*/
public void merge(int[] arr, int low, int middle, int high) {// 用于存储归并后的临时数组int[] temp = new int[high - low + 1];// 记录第一个数组中需要遍历的下标int i = low;// 记录第二个数组中需要遍历的下标int j = middle + 1;// 记录在临时数组中存放的下标int index = 0;// 遍历两个数组,取出小的数字,放入临时数组中while (i <= middle && j <= high) {// 第一个数组的数据更小if (arr[i] <= arr[j]) {// 把更小的数据放入临时数组中temp[index] = arr[i];// 下标向后移动一位i++;} else {temp[index] = arr[j];j++;}index++;}// 处理剩余未比较的数据while (i <= middle) {temp[index] = arr[i];i++;index++;}while (j <= high) {temp[index] = arr[j];j++;index++;}// 把临时数组中的数据重新放入原数组for (int k = 0; k < temp.length; k++) {arr[k + low] = temp[k];}
}
/*** 归并排序*/
public void mergeSort(int[] arr, int low, int high) {int middle = (high + low) / 2;if (low < high) {// 处理左边数组mergeSort(arr, low, middle);// 处理右边数组mergeSort(arr, middle + 1, high);// 归并merge(arr, low, middle, high);}
}
六、基数排序
基数排序的原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。为此需要将所有待比较的数值统一为同样的数位长度,数位不足的数在高位补零。

/*** 基数排序** @param arr*/
public void radixSort(int[] arr) {// 存放数组中的最大数字int max = Integer.MIN_VALUE;for (int value : arr) {if (value > max) {max = value;}}// 计算最大数字是几位数int maxLength = (max + "").length();// 用于临时存储数据(0-9)int[][] temp = new int[10][arr.length];// 用于记录在 temp 中相应的下标存放数字的数量(0-9)int[] counts = new int[10];// 根据最大长度的数决定比较次数(从低位往高位以此比较)for (int i = 0, n = 1; i < maxLength; i++, n *= 10) {// 每一个数字分别计算余数for (int value : arr) {// 计算余数int remainder = value / n % 10;// 把当前遍历的数据放到指定的数组中temp[remainder][counts[remainder]] = value;// 记录数量counts[remainder]++;}// 记录取的元素需要放的位置int index = 0;// 把数字取出来for (int k = 0; k < counts.length; k++) {// 记录数量的数组中当前余数记录的数量不为 0if (counts[k] != 0) {// 循环取出元素for (int l = 0; l < counts[k]; l++) {arr[index] = temp[k][l];// 记录下一个位置index++;}// 把数量置空counts[k] = 0;}}}
}
七、桶排序
桶排序(Bucket Sort)又称箱排序,是一种比较常用的排序算法。其算法原理是将数组分到有限数量的桶里,再对每个桶分别排好序(可以是递归使用桶排序,也可以是使用其他排序算法将每个桶分别排好序),最后一次将每个桶中排好序的数输出。
桶排序的思想就是把待排序的数尽量均匀地放到各个桶中,再对各个桶进行局部的排序,最后再按序将各个桶中的数输出,即可得到排好序的数。
- 首先确定桶的个数。因为桶排序最好是将数据均匀地分散在各个桶中,那么桶的个数最好是应该根据数据的分散情况来确定。首先找出所有数据中的最大值mx和最小值mn;根据mx和mn确定每个桶所装的数据的范围 size,有size = (mx - mn) / n + 1,n为数据的个数,需要保证至少有一个桶,故而需要加个1;
求得了size即知道了每个桶所装数据的范围,还需要计算出所需的桶的个数cnt,有cnt = (mx - mn) / size + 1,需要保证每个桶至少要能装1个数,故而需要加个1;
- 求得了size和cnt后,即可知第一个桶装的数据范围为 [mn, mn + size),第二个桶为 [mn + size, mn + 2 * size),…,以此类推因此步骤2中需要再扫描一遍数组,将待排序的各个数放进对应的桶中。
- 对各个桶中的数据进行排序,可以使用其他的排序算法排序,例如快速排序;也可以递归使用桶排序进行排序;
- 将各个桶中排好序的数据依次输出,最后得到的数据即为最终有序。
/*** 桶排序** @param arr*/
public void bucketSort(int[] arr) {int n = arr.length;int mn = arr[0], mx = arr[0];// 找出数组中的最大最小值for (int i = 1; i < n; i++) {mn = Math.min(mn, arr[i]);mx = Math.max(mx, arr[i]);}// 每个桶存储数的范围大小,使得数尽量均匀地分布在各个桶中,保证最少存储一个int size = (mx - mn) / n + 1;// 桶的个数,保证桶的个数至少为1int cnt = (mx - mn) / size + 1;// 声明cnt个桶List<Integer>[] buckets = new List[cnt];for (int i = 0; i < cnt; i++) {buckets[i] = new ArrayList<>();}// 扫描一遍数组,将数放进桶里for (int k : arr) {int idx = (k - mn) / size;buckets[idx].add(k);}// 对各个桶中的数进行排序,这里用库函数快速排序for (int i = 0; i < cnt; i++) {// 默认是按从小打到排序// 这里可以用任何的方式排序,这里直接用List的sort方法buckets[i].sort(null);}// 依次将各个桶中的数据放入返回数组中int index = 0;for (int i = 0; i < cnt; i++) {for (int j = 0; j < buckets[i].size(); j++) {arr[index++] = buckets[i].get(j);}}
}
排序算法对比
| 排序算法 | 时间复杂度(平均) | 时间复杂度(最坏) | 时间复杂度(最好) | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O(n2) | O(n2) | O(n) | O(1) | 稳定 |
| 选择排序 | O(n²) | O(n²) | O(n²) | O(1) | 不稳定 |
| 插入排序 | O(n²) | O(n²) | O(n) | O(1) | 稳定 |
| 快速排序 | O(nlogn) | O(n²) | O(nlogn) | O(nlogn) | 不稳定 |
| 堆排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | 不稳定 |
| 希尔排序 | O(n^1.3) | O(n²) | O(n) | O(1) | 不稳定 |
| 归并排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | 稳定 |
| 基数排序 | O(d(n+k)) | O(d(n+k)) | O(d(n+k)) | O(n+k) | 稳定 |
| 桶排序 | O(n+k) | O(n²) | O(n) | O(n+k) | 稳定 |
参考资料:https://mp.weixin.qq.com/s?__biz=MzAxMjY5NDU2Ng==&mid=2651862169&idx=1&sn=e011e79ff77736dfb389084bb3a20d37&chksm=804971d0b73ef8c649d7c9b08706f3c33b0e10c3935e24982337b05d69f1487ace072fbd48d9&scene=27
相关文章:

【动画图解】一次理清九大排序算法!面试官问到再也不慌!
排序算法 交换排序 冒泡排序快速排序 插入排序 直接插入排序希尔排序 选择排序 简单选择排序堆排序 归并排序基数排序桶排序 一、冒泡排序 冒泡排序是一种简单的交换排序算法,以升序排序为例,其核心思想是: 从第一个元素开始,…...

组播地址段及其作用
作用 组播(Multicast)传输:在发送者和每一接收者之间实现点对多点网络连接。如果一台发送者同时给多个的接收者传输相同的数据,也只需复制一份的相同数据包。它提高了数据传送效率。减少了骨干网络出现拥塞的可能性。 地址段 组播协议的地址在 IP 协议中属于 D 类…...

Vue+ElementUI前端添加展开收起搜索框按钮
1、搜索框添加判断 v-if"advanced" <el-form-item label"创建日期" v-if"advanced"><el-date-pickerv-model"daterangeLedat"size"small"style"width: 240px"value-format"yyyy-MM-dd"type&q…...

速盾网络:sdk游戏盾有什么作用?
速盾cdn是一款非常优秀的CDN加速服务,它能够帮助游戏开发者们提升游戏的性能和稳定性。其中,速盾cdn的sdk游戏盾是其一项非常实用的功能,它能够为游戏提供更加稳定和快速的网络连接。 首先,让我们来了解一下什么是sdk游戏…...

理解BeEF的架构
BeEF的组件和工作原理BeEF(The Browser Exploitation Framework)是一款用于浏览器渗透测试和漏洞利用的强大工具。它由多个组件组成,这些组件协同工作以实现对受害者浏览器的控制和攻击。本文将深入探讨BeEF的各个组件和其工作原理࿰…...

esp32-s3训练自己的数据进行目标检测、图像分类
esp32-s3训练自己的数据进行目标检测、图像分类 一、下载项目二、环境三、训练和导出模型四、部署模型五、存在的问题 esp-idf的安装参考我前面的文章: esp32cam和esp32-s3烧录human_face_detect实现人脸识别 一、下载项目 训练、转换模型:ModelAssist…...
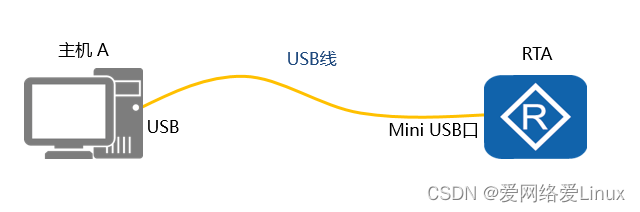
华为设备VRP基础
交换机可以隔离冲突域,路由器可以隔离广播域,这两种设备在企业网络中应用越来越广泛。随着越来越多的终端接入到网络中,网络设备的负担也越来越重,这时网络设备可以通过华为专有的VRP系统来提升运行效率。通用路由平台VRP…...

论文笔记 | ICLR 2023 WikiWhy:回答和解释因果问题
文章目录 一、前言二、主要内容三、总结🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 一、前言 ICLR 2023 | Accept: notable-top-5%:《WikiWhy: Answering and Explaining Cause-and-Effect Questions》 一段话总结:WikiWhy 是一个新的 QA 数据集,围绕一个新的任务…...

LC24. 两两交换链表中的节点
代码随想录 class Solution {// 举例子:假设两个节点 1 -> 2// 那么 head 1; next 2; next.next null// 那么swapPairs(next.next),传入的是null,再下一次递归中直接返回null// 因此 newNode null// 所以 next.next head; > 2.next 1; 2 -> 1// head.next…...

使用redis-rds-tools 工具分析redis rds文件
redis-rdb-tools安装部署及使用 发布时间:2020-07-28 12:33:12 阅读:29442 作者:苏黎世1995 栏目:关系型数据库 活动:开发者测试专用服务器限时活动,0元免费领,库存有限,领完即止&…...
C# Onnx yolov8 plane detection
C# Onnx yolov8 plane detection 效果 模型信息 Model Properties ------------------------- date:2023-12-22T10:57:49.823820 author:Ultralytics task:detect license:AGPL-3.0 https://ultralytics.com/license version&am…...
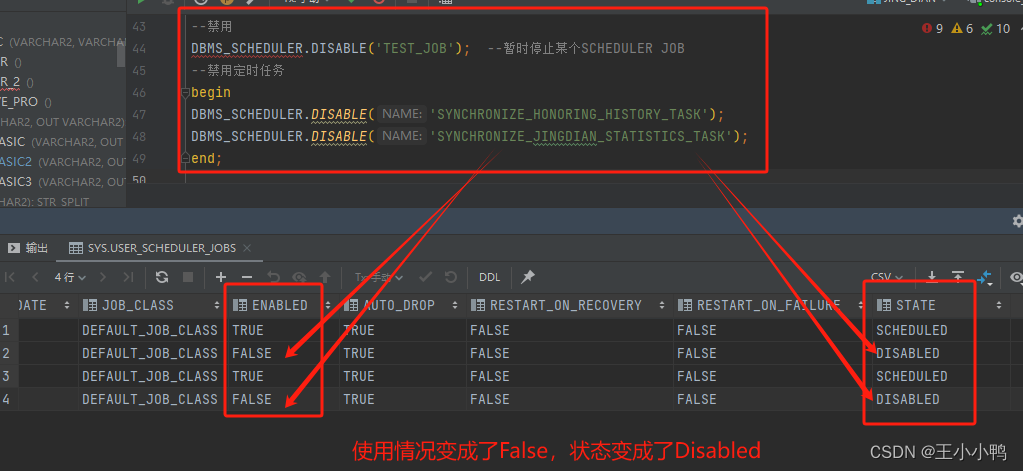
Oracle定时任务的创建与禁用/删除
在开始操作之前,先从三W开始,即我常说的what 是什么;why 为什么使用;how 如何使用。 一、Oracle定时器是什么 Oracle定时器是一种用于在特定时间执行任务或存储过程的工具,可以根据需求设置不同的时间段和频率来执行…...
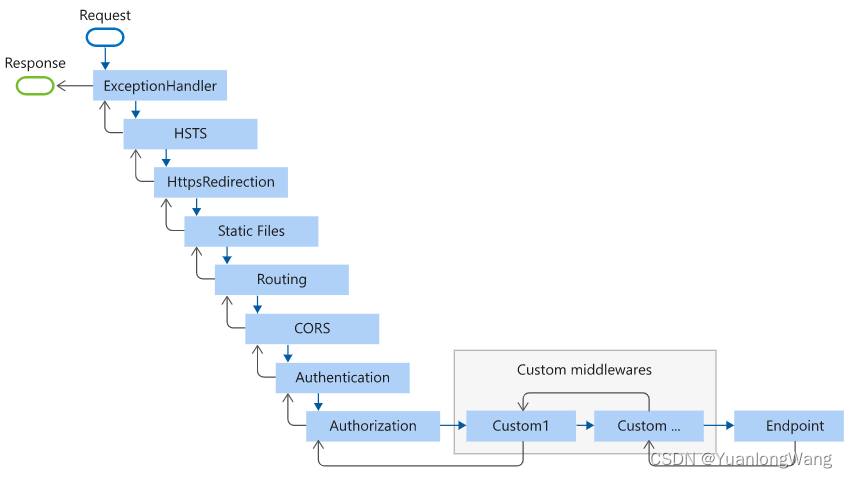
Asp.Net Core 项目中常见中间件调用顺序
常用的 AspNetCore 项目中间件有这些,调用顺序如下图所示: 最后的 Endpoint 就是最终生成响应的中间件。 Configure调用如下: public void Configure(IApplicationBuilder app, IWebHostEnvironment env){if (env.IsDevelopment()){app.UseD…...
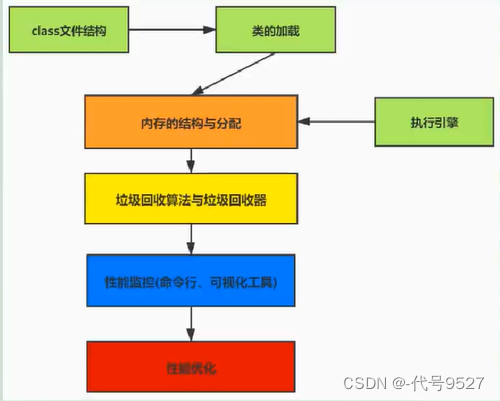
【JVM】一、认识JVM
文章目录 1、虚拟机2、Java虚拟机3、JVM的整体结构4、Java代码的执行流程5、JVM的分类6、JVM的生命周期 1、虚拟机 虚拟机,Virtual Machine,一台虚拟的计算机,用来执行虚拟计算机指令。分为: 系统虚拟机:如VMware&am…...
[SWPUCTF 2021 新生赛]Do_you_know_http已
打开环境 它说用WLLM浏览器打开,使用BP抓包,发送到重发器 修改User-Agent 下一步,访问a.php 这儿他说添加一个本地地址,它给了一个183.224.40.160,我用了发现没用,然后重新添加一个地址:X-Forwa…...

hadoop01_完全分布式搭建
hadoop完全分布式搭建 1 完全分布式介绍 Hadoop运行模式包括:本地模式(计算的数据存在Linux本地,在一台服务器上 自己测试)、伪分布式模式(和集群接轨 HDFS yarn,在一台服务器上执行)、完全分…...

【每日一题】得到山形数组的最少删除次数
文章目录 Tag题目来源解题思路方法一:最长递增子序列 写在最后 Tag 【最长递增子序列】【数组】【2023-12-22】 题目来源 1671. 得到山形数组的最少删除次数 解题思路 方法一:最长递增子序列 前后缀分解 根据前后缀思想,以 nums[i] 为山…...

2023年,为什么汽车依然有很多小毛病?
汽车出现小毛病是一个复杂的问题,其原因涉及到汽车本身的设计、制造质量、维护保养以及使用环境等多个方面。只有汽车制造商、车主和社会各界共同努力,才能够减少汽车的小毛病,提高汽车的可靠性和安全性。 比如,汽车的维护和保养…...

yocto系列讲解[实战篇]93 - 添加Qtwebengine和Browser实例
By: fulinux E-mail: fulinux@sina.com Blog: https://blog.csdn.net/fulinus 喜欢的盆友欢迎点赞和订阅! 你的喜欢就是我写作的动力! 目录 概述集成meta-qt5移植过程中的问题问题1:virtual/libgl set to mesa, not mesa-gl问题2:dmabuf-server-buffer tries to use undecl…...
Python实验报告十一、自定义类模拟三维向量及其运算
一、实验目的: 1、了解如何定义一个类。 2、了解如何定义类的私有数据成员和成员方法。 3、了解如何使用自定义类实例化对象。 二、实验内容: 定义一个三维向量类,并定义相应的特殊方法实现两个该类对象之间的加、减运算(要…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...
