算法基础之表达整数的奇怪方式
表达整数的奇怪方式
中国剩余定理:
-
求M = 所有m之积 然后Mi = M / mi

- x = 如下图 满足要求
- x = 如下图 满足要求
扩展中国剩余定理
-

-
找到x **使得x mod mi = ai**成立
-
对于每两个式子 都可以推出①式
-
即 用扩展欧几里得算法 可以算出k1,-k2和m2–m1
-

-
判无解 : 若**(m2–m1) % d != 0** 说明该等式无解 即原方程无解 本题无解
-
-
找到最小正整数解
- 已知k1的通式(如下图 代入原方程可证成立) 则求最小正整数解 只要 %abs(a2/d)

-
等效替代
-
设a0 = gcd(a1,a2) , m0 = k1 * a1 + m1 得到新的式子和原方程长得一模一样
-

-
也就是说 每两个式子 都可以通过合并的方式 写成一个式子
-
只要将所有n个式子全都合并成一个式子 x = k*a + m 就可以求解x了
-
-
-
#include <iostream>#include <algorithm>using namespace std;typedef long long LL;LL exgcd(LL a,LL b,LL &x,LL &y){ //拓展欧几里得算法if(!b){x=1,y=0;return a;}LL d=exgcd(b,a%b,y,x);y-=a/b*x;return d;}int main(){int n;cin>>n;LL x=0,m1,a1;cin>>a1>>m1;for(int i=0;i<n-1;i++){ //输入n-1次LL m2,a2;cin>>a2>>m2;LL k1,k2;LL d=exgcd(a1, a2,k1,k2);if((m2-m1) % d) //无解{x = -1;break;}k1 *= (m2-m1) / d; //k1乘相应系数k1 = (k1 %(a2/d) + a2 / d) % (a2/d); //见下方注释x = k1 * a1 + m1; //根据公式③//更新a1 m1 进行下一次合并m1 = k1 * a1 + m1;a1 = abs(a1 * a2 /d);}if(x!=-1) x=(m1%a1+a1)%a1; //若x为负数 将x变成正数cout<<x<<endl;return 0;}- k1 = (k1 %(a2/d) + a2 / d) % (a2/d);
- c++中 若k1为负数 %完 仍然是负数 而不是正数 因此 我们在%完后 +上一个膜数 再膜一次
- 就可以求出最小正整数k1
- k1 = (k1 %(a2/d) + a2 / d) % (a2/d);
参考题解 :https://www.acwing.com/solution/content/3539/
相关文章:

算法基础之表达整数的奇怪方式
表达整数的奇怪方式 中国剩余定理: 求M 所有m之积 然后Mi M / mi x 如下图 满足要求 扩展中国剩余定理 找到x **使得x mod mi ai**成立 对于每两个式子 都可以推出①式 即 用扩展欧几里得算法 可以算出k1,-k2和m2–m1 判无解 : 若**(m2–m1) % d ! 0** 说明该等式无解 …...
WEB 3D技术 three.js 设置图像随窗口大小变化而变化
本文 我们来讲讲我们图层适应窗口变化的效果 可能这样说有点笼统 那么 自适应应该大家更熟悉 就是 当我们窗口发生变化说 做一些界面调整比例 例如 我们这样一个i项目界面 我们打开 F12 明显有一部分被挡住了 那么 我们可以刷新 这样是正常了 但是 我们将F12关掉 给F12的…...
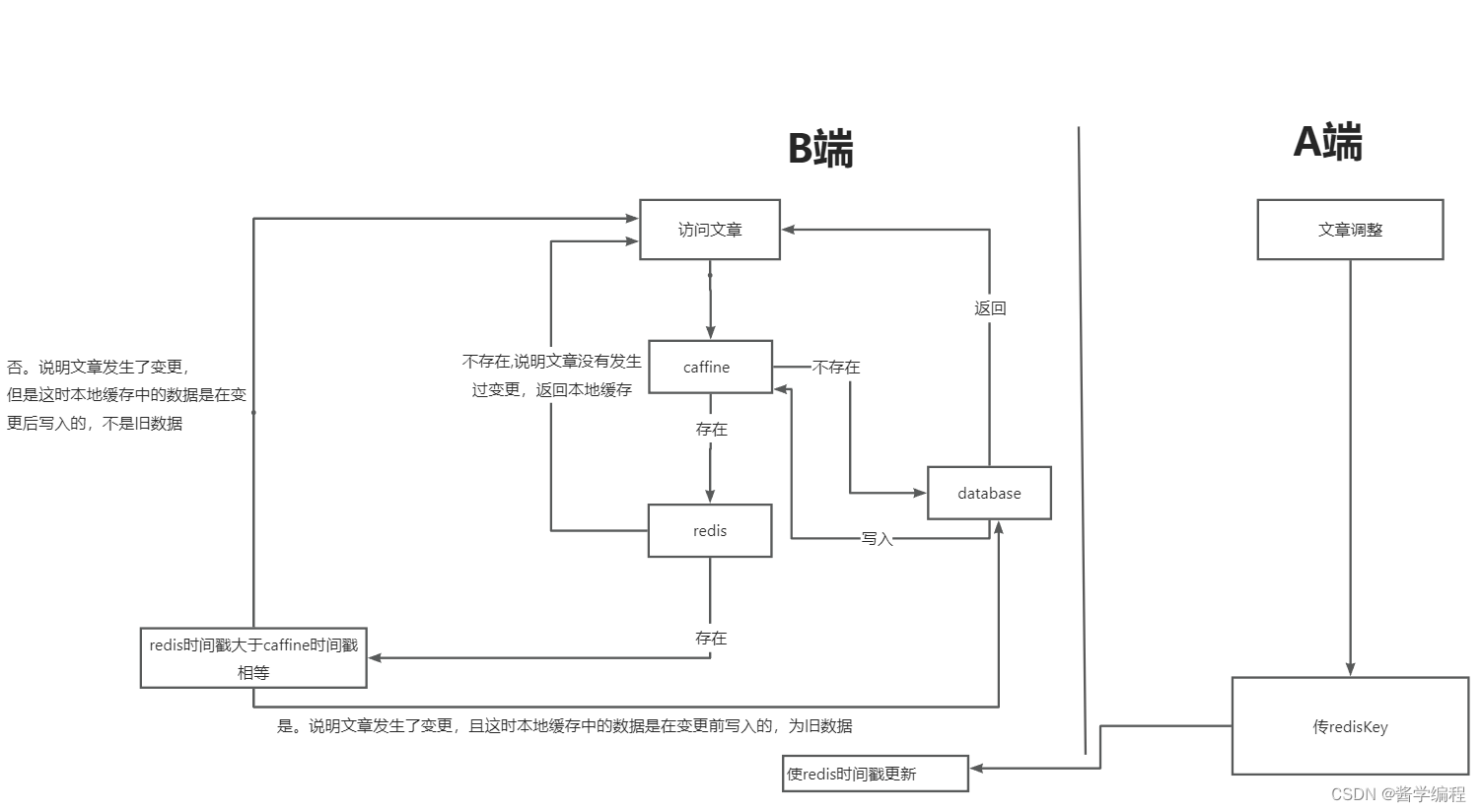
实战案例:缓存不一致问题的解决(redis+本地缓存caffine)
一.问题引入 目前在写项目的时候,在B端查看文章,A端修改文章。为了增加效率,以及防止堆内存溢出,在B端选择本地缓存文章的方案。但是目前出现了A端对文章修改之后,B端读的还是旧数据,出现了缓存不一致的问…...

【开源CDP】市场增长未来的探索,开源CDP带来的技术崛起与变革
数字化趋势之下,数据成了企业竞争的核心资源,不管是公域还是私域,网络俨然成了品牌打响市场的一线战场,然而,在这场数字战役里,许多企业不得不面临一个共同问题:数据零散、分散、平台众多、无法…...
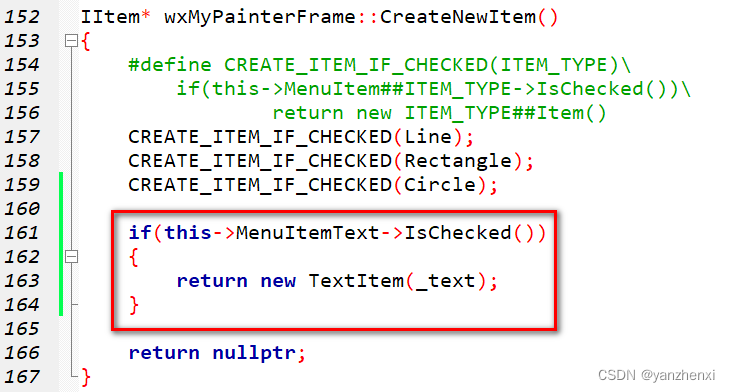
第11章 GUI Page423~424 步骤六 支持文字,使用菜单,对话框输入文字
运行效果: 点击OK,然后再窗口上按住左键,拖动鼠标 关键代码: 新增头文件和成员,新增私有成员_text 成员初始化 为菜单项MenuItemText添加响应函数 新增创建TextItem()的代码...

【Qt】Qt Creator 警告: Unused parameter ‘xxx‘
1. 问题 Qt开发中,有些函数参数没有使用,会报Unused parameter xxx警告,这个警告不影响代码正常运行。 2. 屏蔽这个警告的方法 2.1 方法1 函数中添加 Q_UNUSED(arg); TestClass::TestClass(QObject *parent) {Q_UNUSED(parent); }2.2 方…...

「Vue3面试系列」Vue3.0性能提升主要是通过哪几方面体现的?
文章目录 一、编译阶段diff算法优化静态提升事件监听缓存SSR优化 二、源码体积三、响应式系统参考文献 一、编译阶段 回顾Vue2,我们知道每个组件实例都对应一个 watcher 实例,它会在组件渲染的过程中把用到的数据property记录为依赖,当依赖发…...

网络结构模式
一、C/S结构 服务器 - 客户机,即 Client - Server ( C/S )结构。 C/S 结构通常采取两层结构。服务器负责数据的 管理,客户机负责完成与用户的交互任务。客户机是因特网上访问别人信息的机器,服务器则是提 供信息供人…...

IIC及OLED实验
I2C (Inter-Integrated Circuit): I2C 是一种用于在芯片之间进行短距离数字通信的串行通信协议。它允许多个设备通过两根导线(一根数据线 SDA 和一根时钟线 SCL)进行通信。I2C 常常用于嵌入式系统中连接传感器、存储器、显示屏和其他外设。 数据线和时钟…...

day6 力扣公共前缀--go实现---对字符串的一些思考
今日份知识: curl -x 指定方法名 请求的url -d 请求体body里面的内容 //curl命令 curl -x Get 127.0.0.1:8080/add/user -d jinlicurl如果不指定方法,默认使用get方法,在go里面,get方法到底可以不可以把内容数据写在body里面传…...
27.Java程序设计-基于Springboot的在线考试系统小程序设计与实现
1. 引言 随着数字化教育的发展,在线考试系统成为教育领域的一项重要工具。本论文旨在介绍一个基于Spring Boot框架的在线考试系统小程序的设计与实现。在线考试系统的开发旨在提高考试的效率,简化管理流程,并提供更好的用户体验。 2. 系统设…...

Redis可视化工具Redis Desktop Manager mac功能特色
Redis Desktop Manager mac是一款非常实用的Redis可视化工具。RDM支持SSL / TLS加密,SSH隧道,基于SSH隧道的TLS,为您提供了一个易于使用的GUI,可以访问您的Redis数据库并执行一些基本操作:将键视为树,CRUD键…...

【C++】揭开运算符重载的神秘面纱
目录 一、引言 优点 二、介绍 1.定义 2.语法 三、示例 1.加法运算符重载 2.一元运算符重载 3.友元函数 4.流插入和流提取 5.自增自减运算符 总结 一、引言 何为运算符重载?运算符重载,是C中的一项强大特性,赋予了程序员在自定义类…...
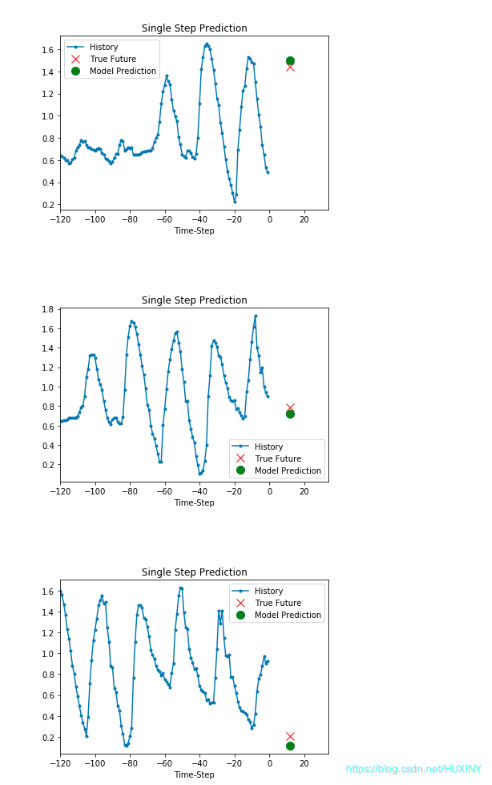
竞赛保研 基于LSTM的天气预测 - 时间序列预测
0 前言 🔥 优质竞赛项目系列,今天要分享的是 机器学习大数据分析项目 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐! 🧿 更多资料, 项目分享: https://gitee.com/dancheng-senior/po…...

前端常用的开发工具
前端常用的开发工具🔖 文章目录 前端常用的开发工具🔖1. Snipaste--截图工具2. ScreenToGif--gif图片录制3. Typora--Markdown编辑器4. notepad--文本代码编辑器5. uTools--多功能工具6. EV录屏--录屏软件7. Xmind--思维导图8. Apifox -- 接口调试9. Tor…...
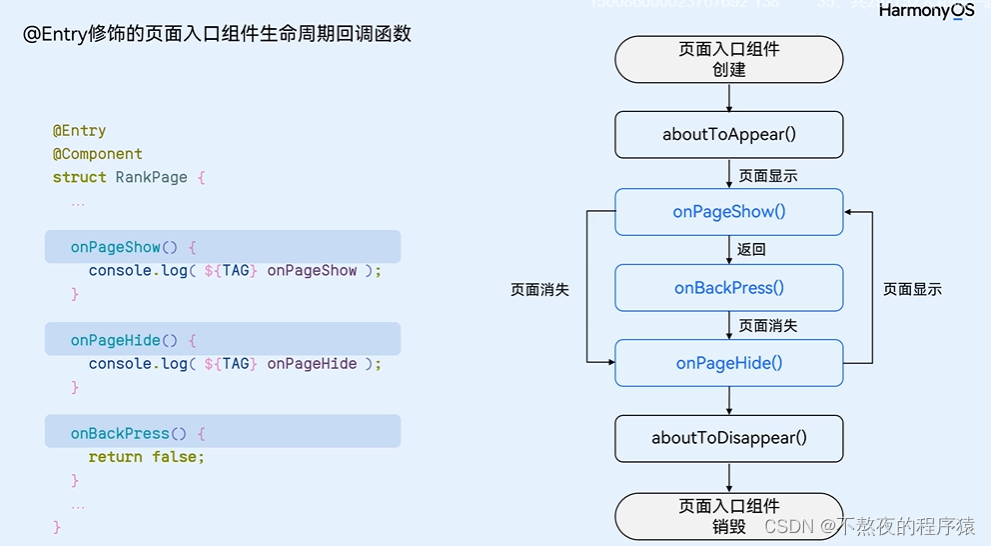
鸿蒙开发语言介绍--ArkTS
1.编程语言介绍 ArkTS是HarmonyOS主力应用开发语言。它在TypeScript (简称TS)的基础上,匹配ArkUI框架,扩展了声明式UI、状态管理等相应的能力,让开发者以更简洁、更自然的方式开发跨端应用。 2.TypeScript简介 自行补充TypeScript知识吧。h…...

关于“Python”的核心知识点整理大全36
目录 13.4.4 向下移动外星人群并改变移动方向 game_functions.py alien_invasion.py 13.5 射杀外星人 13.5.1 检测子弹与外星人的碰撞 game_functions.py alien_invasion.py 13.5.2 为测试创建大子弹 13.5.3 生成新的外星人群 game_functions.py alien_invasion.py …...
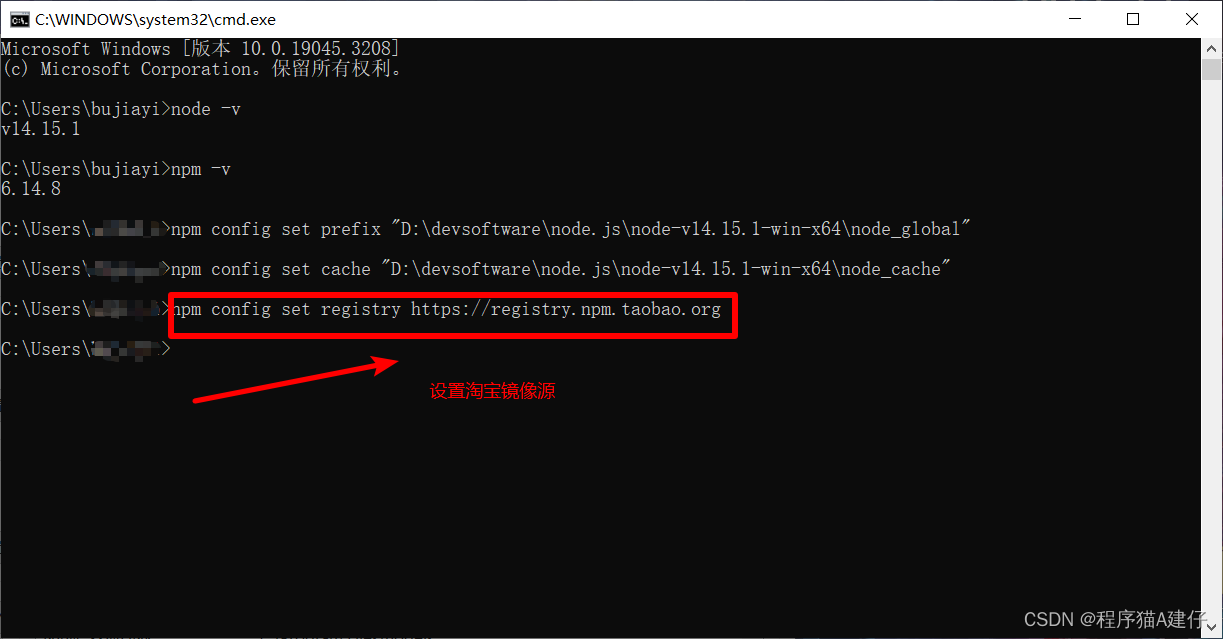
安装nodejs,配置环境变量并将npm设置淘宝镜像源
安装nodejs并将npm设置淘宝镜像源 1. 下载nodejs 个人不喜欢安装包,所以是下载zip包的方式。这里我下载的node 14解压包版本 下载地址如下:https://nodejs.org/dist/v14.15.1/node-v14.15.1-win-x64.zip 想要其他版本的小伙伴去https://nodejs.org/di…...

12.18构建哈夫曼树(优先队列),图的存储方式,一些细节(auto,pair用法,结构体指针)
为结构体自身时,用.调用成员变量;为结构体指针时,用->调用成员变量 所以存在结构体数组时,调用数组元素里的成员变量,就是要用. 结构体自身只有在new时才会创建出来,而其指针可以随意创建 在用new时&…...
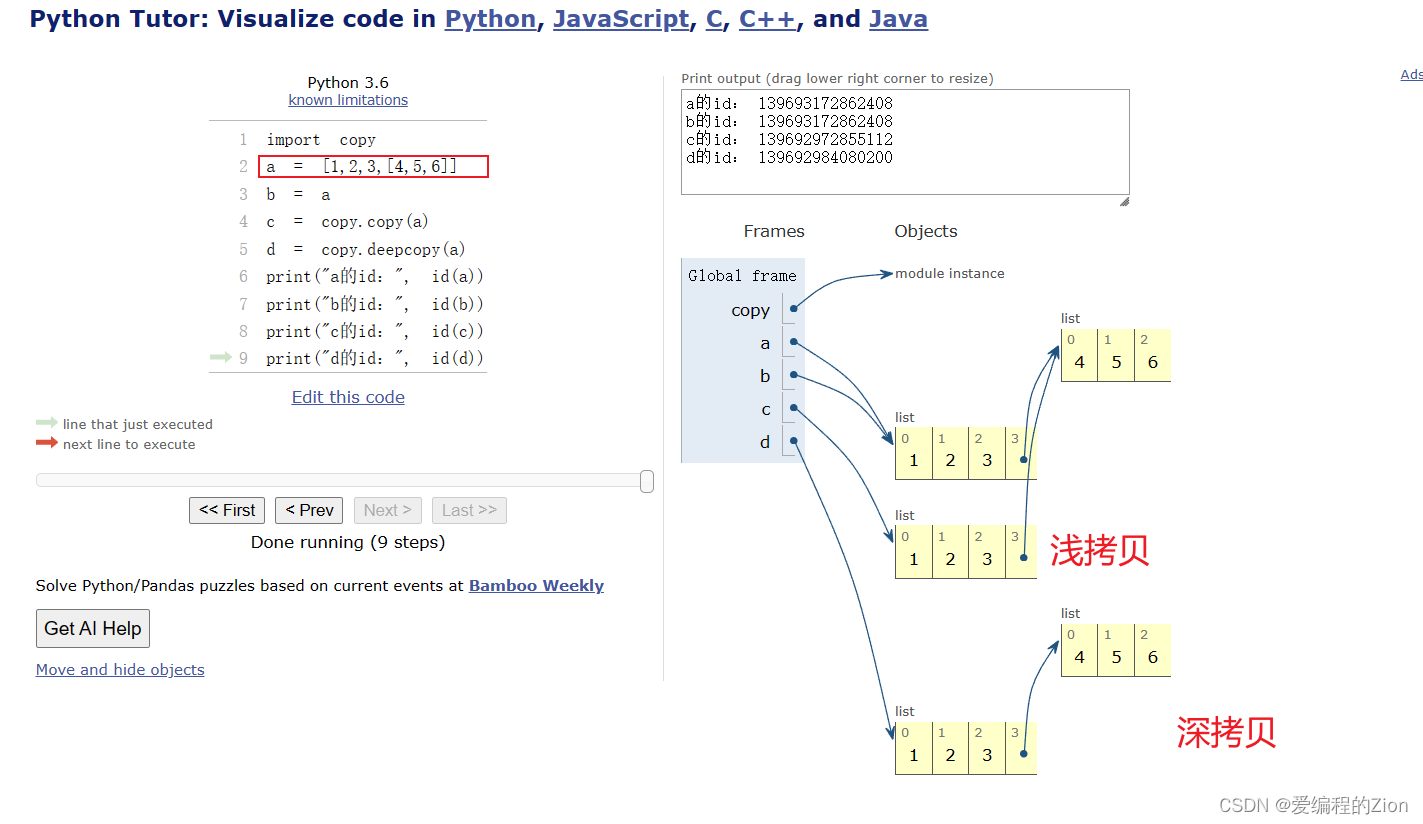
《Python》面试常问:深拷贝、浅拷贝、赋值之间的关系(附可变与不可变)【用图文讲清楚!】
背景 想必大家面试或者平时学习经常遇到问python的深拷贝、浅拷贝和赋值之间的区别了吧?看网上的文章很多写的比较抽象,小白接收的难度有点大,于是乎也想自己整个文章出来供参考 可变与不可变 讲深拷贝和浅拷贝之前想讲讲什么是可变数据类型…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

k8s从入门到放弃之Pod的容器探针检测
k8s从入门到放弃之Pod的容器探针检测 在Kubernetes(简称K8s)中,容器探测是指kubelet对容器执行定期诊断的过程,以确保容器中的应用程序处于预期的状态。这些探测是保障应用健康和高可用性的重要机制。Kubernetes提供了两种种类型…...

