大话数据结构-普里姆算法(Prim)和克鲁斯卡尔算法(Kruskal)
5 最小生成树
构造连通网的最小代价生成树称为最小生成树,即Minimum Cost Spanning Tree,最小生成树通常是基于无向网/有向网构造的。
找连通网的最小生成树,经典的有两种算法,普里姆算法和克鲁斯卡尔算法。
5.1 普里姆(Prim)算法
普里姆算法,即Prim算法,大致实现过程如下:
(1) 新建数组adjVex[n],初始值均为0;新建数组lowCost[n],初始值均为infinity;
(2) 从第一个顶点X(下标为0)开始,把它与各顶点连接的权记录下来,放到lowCost数组里面,然后找到权最小的那个顶点Y,得到最小生成树的第一条边(X,Y),然后把lowCost数组里面Y对应的下标的元素设置为0;
(3) 然后处理顶点Y,把它与除X外的其他各顶点连接的权,与lowCost数组下标相同的权比较,将小的放入到lowCost里面,并把较小的权对应的顶点的下标记录在adjVex数组里面,也即,adjVex[j]要么是Y,要么是除X外的其他顶点;
(4) 找到lowCost数组中权最小的那个(显然不会是X,也不会是Y),得到最小生成树的第二条边(adjVex[j],j),然后把lowCost[j]设置为0;
(5) 然后按(3)、(4)的规则,处理第j个顶点,直到所有顶点都被连接起来(注意,最小连通树是针对连通网的);
下面我们会根据各种存储方式进行举例。
5.1.1 邻接矩阵的最小生成树
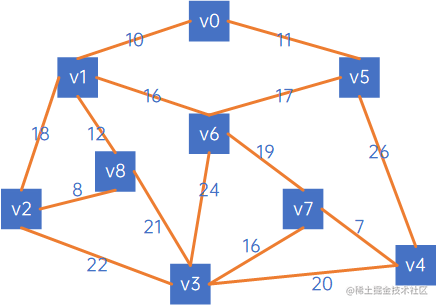
假设有以下无向网:
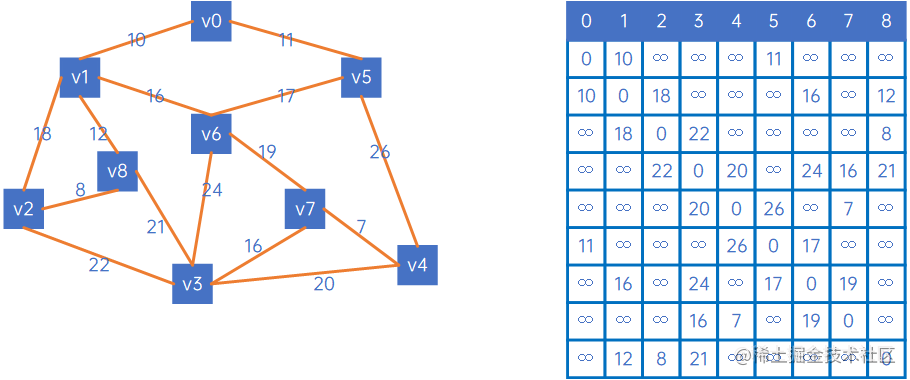
我们定义两个数组,一个X={},Y={V0、v1、v2、v3、v4、v5、v6、v7、v8},其中X表示已连通的顶点,Y表示未连通的顶点。
先从第一个顶点v0开始,把它加入X,表示已连通,这时,X={v0},Y={v1、v2、v3、v4、v5、v6、v7、v8}。
接下来,看X中的V0与其他顶点关联时权值情况,发现(v0,v1)的权值最小,因此认为,v0和v1是最小生成树的一个边,此时X={v0、v1},Y={v2、v3、v4、v5、v6、v7、v8}:
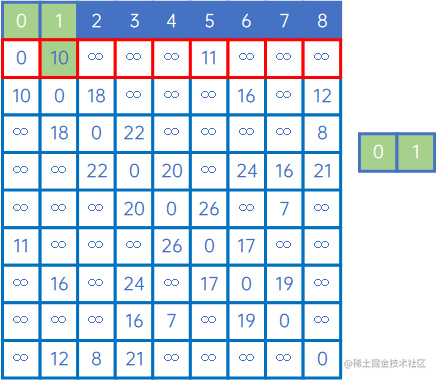
然后,再看X中的所有顶点与Y中的所有顶点的权值,发现边现(V0,v5)之间的权值最小,因此认为(V0,v5)是最小生成树的一条边,此时X={v0、v1、v5},Y={v2、v3、v4、v6、v7、v8}:
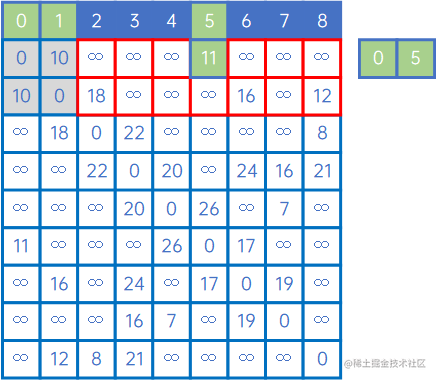
然后,再看X中的所有顶点与Y中的所有顶点的权值,发现边现(V1,v8)之间的权值最小,因此认为(V1,v8)是最小生成树的一条边,此时X={v0、v1、v5、v8},Y={v2、v3、v4、v6、v7}:
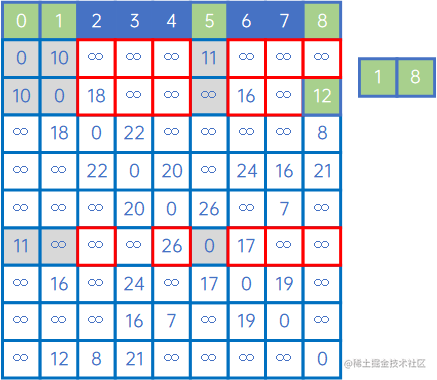
然后,再看X中的所有顶点与Y中的所有顶点的权值,发现边现(V8,v2)之间的权值最小,因此认为(V8,v2)是最小生成树的一条边,此时X={v0、v1、v5、v8、v2},Y={v3、v4、v6、v7}:
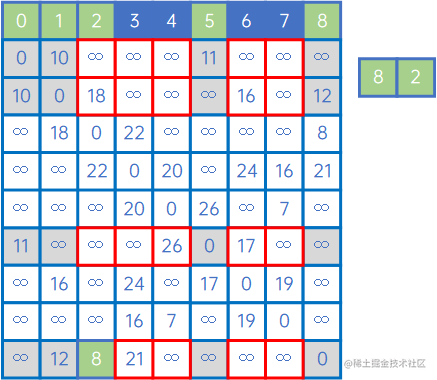
然后,再看X中的所有顶点与Y中的所有顶点的权值,发现边现(V1,v6)之间的权值最小,因此认为(V1,v6)是最小生成树的一条边,此时X={v0、v1、v5、v8、v2、v6},Y={v3、v4、v7}:
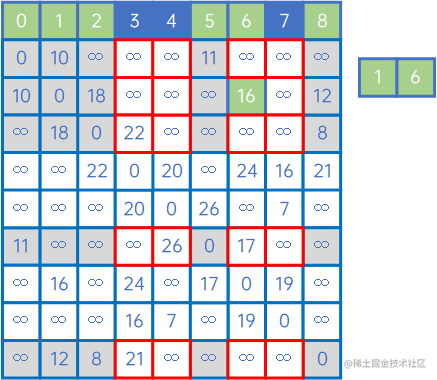
然后,再看X中的所有顶点与Y中的所有顶点的权值,发现边现(V6,v7)之间的权值最小,因此认为(V6,v7)是最小生成树的一条边,此时X={v0、v1、v5、v8、v2、v6、v7},Y={v3、v4}:
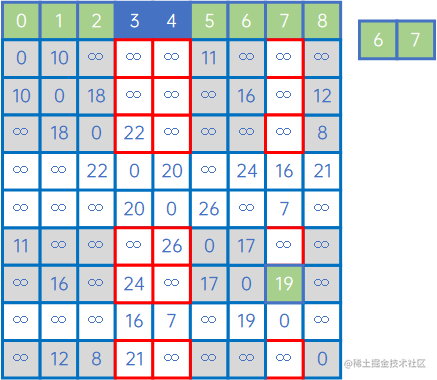
然后,再看X中的所有顶点与Y中的所有顶点的权值,发现边现(V7,v4)之间的权值最小,因此认为(V7,v4)是最小生成树的一条边,此时X={v0、v1、v5、v8、v2、v6、v7、v4},Y={v3}:
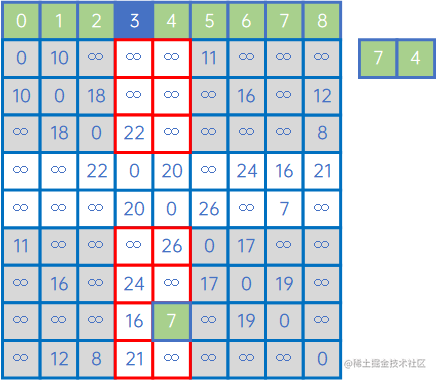
然后,再看X中的所有顶点与Y中的所有顶点的权值,发现边现(V7,v3)之间的权值最小,因此认为(V7,v3)是最小生成树的一条边,此时X={v0、v1、v5、v8、v2、v6、v7、v4、v3},Y={}:
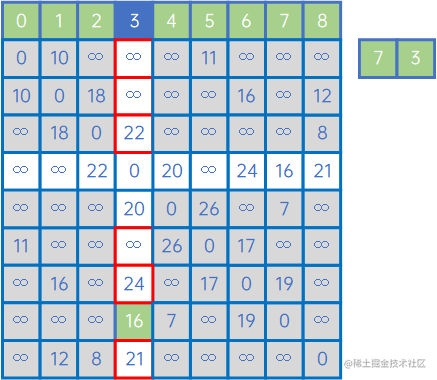
这时,Y已处理完毕,所有顶点都连起来了,形成了最小生成树。
观察一下,我们在获取最小生成树的边时,第一步是从arc[0][j]取权最小的,取到了(v0,v1),第二步,是从arc[0][j]和arc[1][j]中取权值最小的,取到了(v0,v5),第三步,是从arc[0][j]、arc[1][j]和arc[5][j]中取权最小的,取到了(v1,v8),也即,规则是:
(1) 从arc[0][j]中取最小权对应的边(v0,v1),此时X={v0},把v1加入到X中;
(2) 从arc[0][j]、arc[1][j]中取最小权对应的边(v0,v5),此时X={v0,v1},把v5加入到X中;
(3) 从arc[0][j]、arc[1][j]、arc[5][j]中取最小权对应的边(v1,v8),此时X={v0,v1,v5},把v8加入到X中;
(4) 从arc[0][j]、arc[1][j]、arc[5][j]…arc[x][j]中取最小权对应的边(vi,vk),然后判断vi和vk是否在X中,不在则加入到X中;
当在arc[0][j]、arc[1][j]、arc[5][j]…arc[x][j]中取最小的权时,我们要比较x个一元数组的值,我们再做一下优化:
(1) 从arc[0][j]中取最小权对应的边(v0,v1),此时X={v0},把v1加入到X中;
(2) 从arc[0][j]、arc[1][j]中取最小权对应的边(v0,v5),此时X={v0,v1},把v5加入到X中,然后我们把arc[0][j]、arc[1][j]组合一下,取出arc[0][j]、arc[1][j]中较小的权放到lowCost[j]里面,同时使用一个数组adjVex[j]记录lowCost[j]对应的起始顶点下标,同时标注lowCost[0]、lowCost[1]的值为负无穷大,如下:
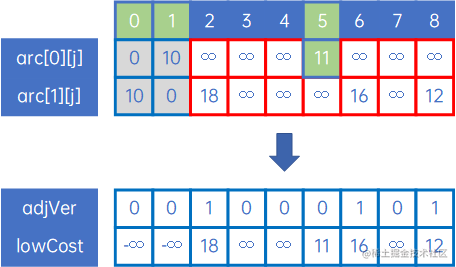
(3) 这时,只需要从lowCost[j]、arc[5][j]中取最小权对应的边就行了,不用再迭代arc[0][j]和arc[1][j];
因此,我们定义两个数组,lowCost[n]表示已处理过的顶点跟其他顶点之间的权值最小值列表,其中已处理过的顶点之间的权值设置为负无穷大,adjVex[n]表示最小权值对应的起始顶点,我们重新来看看上述无向网。
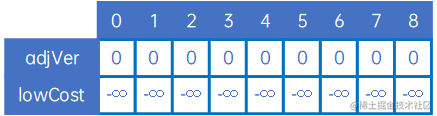
第一步,定义lowCost[n]和adjVex[n],adjVex[n]默认值为0,lowCost[n]默认值为负无穷大:
接下来处理第一个顶点,找到第一个顶点与其他顶点中权值最小的那条边(自身除外),具体做法是,令adjVex[n]的元素均为0,令lowCost[n]的元素值为arc[0][j],然后找到权值最小的arc[0][x],取边(adjVex[x],x),即(v0,v1):
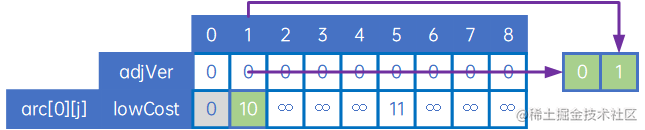
接下来,要比较的应是arc[0][j]和arc[1][j]中,除arc[0][0]、arc[0][1]、arc[1][0]和arc[1][1]外的其他值,取最小值,因为我们要取的是“其他顶点与顶点v0、v1中权值最小的边”,因此我们把arc[1][j]与lowCost[n](这时,lowCost即为arc[0][j])比较,把较小的写入到lowCost中,同时把较小权对应对应的顶点下标写入到adjVex[n]中,如下:
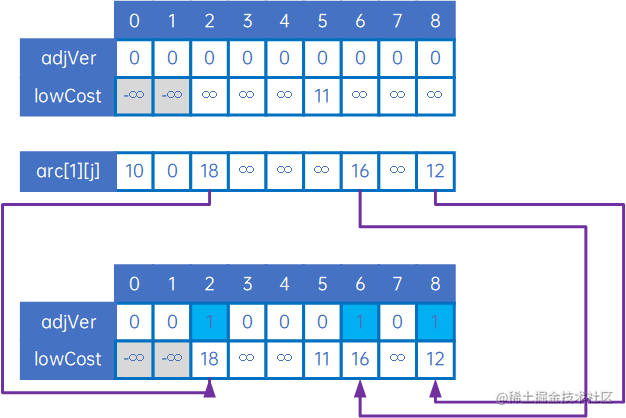
如上可知,arc[1][2]小于lowCost[2],因此令lowCost[2]=arc[1][2]、adjVex[2]=1,arc[1][6]和arc[1][8]也相似处理。
然后,我们取出其中的最小权,得到下一条最小生成树的边,即(v0,v5):
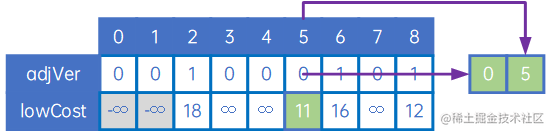
接下来,是取得顶点v0、v1、v5与其他顶点的权中的最小值,生成下一条边,整体处理方式与上文类似:
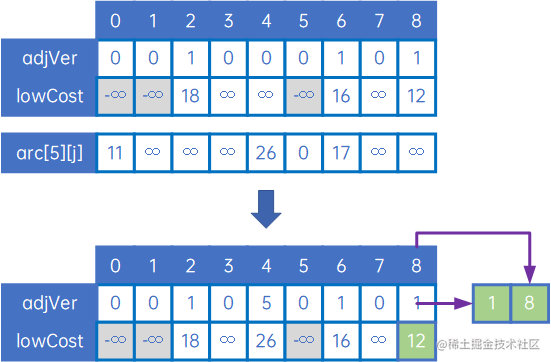
后续操作也类似,直到所有顶点处理完毕,得到最小生成树。
让我们来看有向网的处理,按上述过程处理,得到以下结果:
即:
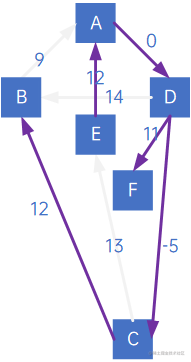
但注意观察,同样是连通B顶点,弧<B,A>实际上比<C,B>权小,所以最小生成树应该为:
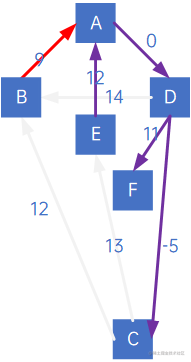
因此,有向树的最小生成树生成过程中,不仅要看“顶点X指向的顶点中权最小的”,还要看“顶点X被指向的顶点中权最小的”。
因此,寻找最低代码的边/弧的逻辑应是“找到该顶点指向的即该顶点被指向的顶点中,代价最小的边或弧”,对于无向网当然这两个概念是一样的,但对于有向网,则要进行双向处理,因此上述有向网的处理逻辑有所不同。
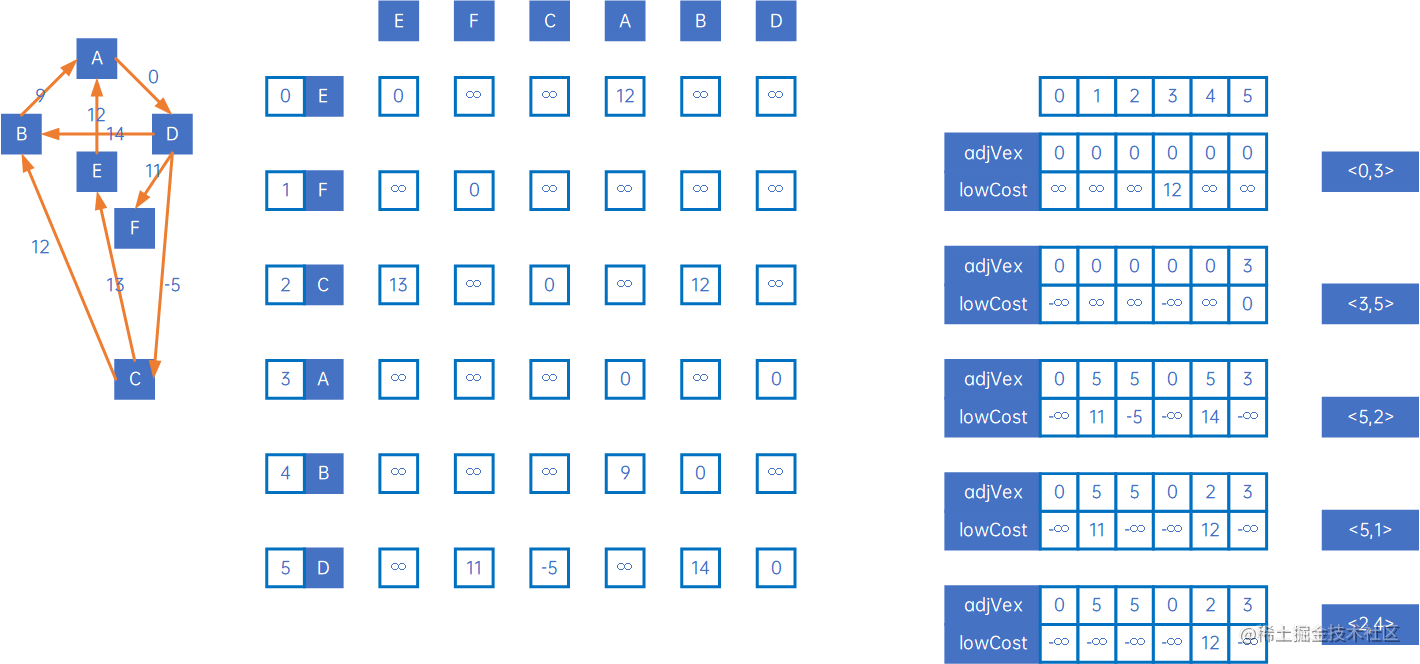
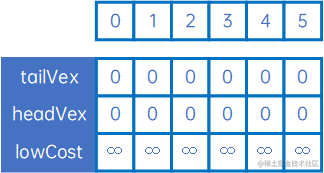
以以上有向网为例,第一步,定义三个数组:lowCost与无向网相同,tailVex和headVex代替adjVex,分别表示箭头的尾巴和头(若为无向网则尾巴和头可以任意),初始化tailVex和headVex为0,lowCost为无穷大:
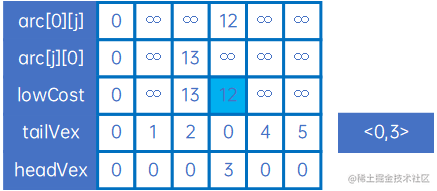
然后使用arc[0][j]和arc[j][0]与lowCost比较,取小的权,并记录箭头的尾巴和头,可取出最小的权对应的尾巴和头,得到最小生成树的第一条弧<0,3>,然后设置lowCost[0]和lowCost[3]为负无穷大,表示这两个顶点已连通:
然后取arc[3][j]和arc[j][3],重复上述处理,得到下一条弧<3,5>,然后设置lowCost[3]和lowCost[5]为负无穷大,表示这两个顶点已连通:
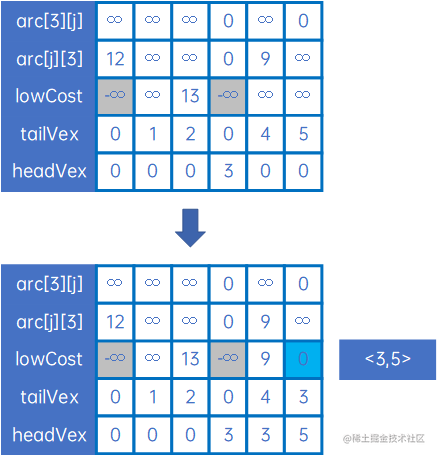
然后对arc[5][j]和arc[j][5]做类似处理,一直到所有顶点都连通。
代码实现如下所示:
/*** 生成最小生成树** @param visitedVal 已访问的顶点被标记的值* @return 最小生成树的边或弧列表* @author Korbin* @date 2023-02-07 15:23:14**/
@SuppressWarnings("unchecked")
public List<String> minimumCostSpanningTree(W visitedVal) {List<String> result = new ArrayList<>();if (type.equals(BusinessConstants.GRAPH_TYPE.UNDIRECTED) ||type.equals(BusinessConstants.GRAPH_TYPE.DIRECTED)) {// 最小生成树只针对网return null;}// 用于存储“当前检查的顶点X与顶点j的权W(X,j)”及“顶点tailVex[j]到顶点headVex[j]的权W(adj[j],j)”中较优(如果是数值的话就是较小)的那个权W[] lowCost = (W[]) Array.newInstance(infinity.getClass(), vertexNum);for (int i = 0; i < vertexNum; i++) {lowCost[i] = infinity;}// 用于存储箭头的尾和头int[] tailVex = new int[vertexNum];int[] headVex = new int[vertexNum];// 取权最小的,即第一个顶点与其他顶点之间权最小的顶点int index = 0;int connectedNum = 0;boolean[] visited = new boolean[vertexNum];while (connectedNum < vertexNum) {// 其他顶点是与lowCost比较,取小的W minWeight = null;int newIndex = index;for (int i = 0; i < vertexNum; i++) {if (i != index && !lowCost[i].equals(visitedVal) && arc[index][i].compareTo(lowCost[i]) < 0) {lowCost[i] = arc[index][i];tailVex[i] = index;headVex[i] = i;}if (type.equals(BusinessConstants.GRAPH_TYPE.DIRECTED_NETWORK)) {// 有向网还需要处理指向本顶点的顶点if (i != index && !lowCost[i].equals(visitedVal) && arc[i][index].compareTo(lowCost[i]) < 0) {lowCost[i] = arc[i][index];tailVex[i] = i;headVex[i] = index;}}// 取出最小的权// 忽略自身// 忽略lowCost[j]为已访问过的顶点if (i != index && !lowCost[i].equals(visitedVal)) {if (null == minWeight || minWeight.compareTo(lowCost[i]) > 0) {minWeight = lowCost[i];newIndex = i;}}}index = newIndex;// 打印取到的边switch (type) {case DIRECTED_NETWORK: {String val = "<" + tailVex[index] + "," + headVex[index] + ">";result.add(val);break;}case UNDIRECTED_NETWORK: {String val = "(" + tailVex[index] + "," + headVex[index] + ")";result.add(val);break;}}// 设置已连通的顶点数if (!visited[tailVex[index]]) {visited[tailVex[index]] = true;connectedNum++;}// 设置该顶点已处理if (!visited[headVex[index]]) {visited[headVex[index]] = true;connectedNum++;}// 设置lowCost[index]为已访问lowCost[tailVex[index]] = visitedVal;lowCost[headVex[index]] = visitedVal;}return result;}
5.1.2 邻接表的最小生成树
邻接表和逆邻接表的处理方式也是类似,只是需要找到指向的和被指向的顶点的权进行比较,另外,邻接表和逆邻接表的处理方式也会有差异:
/*** 生成最小生成树** @param visitedVal 已访问的顶点被标记的值* @return 最小生成树的边或弧列表* @author Korbin* @date 2023-02-07 15:23:14**/
@SuppressWarnings("unchecked")
public List<String> minimumCostSpanningTree(W visitedVal) {List<String> result = new ArrayList<>();if (type.equals(BusinessConstants.GRAPH_TYPE.UNDIRECTED) ||type.equals(BusinessConstants.GRAPH_TYPE.DIRECTED)) {// 最小生成树只针对网return null;}// 用于存储“当前检查的顶点X与顶点j的权W(X,j)”及“顶点adjVex[j]到顶点j的权W(adj[j],j)”中较优(如果是数值的话就是较小)的那个权W[] lowCost = (W[]) Array.newInstance(infinity.getClass(), vertexNum);for (int i = 0; i < vertexNum; i++) {lowCost[i] = infinity;}// 用于存储箭头的尾和头int[] tailVex = new int[vertexNum];int[] headVex = new int[vertexNum];boolean[] visited = new boolean[vertexNum];int connectedNum = 0;int index = 0;while (connectedNum < vertexNum) {for (int i = 0; i < vertexNum; i++) {VertexNode<T, W> vertexNode = vertexes[i];EdgeNode<W> edgeNode = vertexNode.getFirstEdge();while (null != edgeNode) {int refIndex = edgeNode.getIndex();W weight = edgeNode.getWeight();// 邻接表if (i == index && !lowCost[refIndex].equals(visitedVal) &&weight.compareTo(lowCost[refIndex]) < 0) {// 本顶点指向的if (!reverseAdjacency) {tailVex[refIndex] = i;headVex[refIndex] = refIndex;lowCost[refIndex] = weight;} else {tailVex[refIndex] = refIndex;headVex[refIndex] = i;lowCost[refIndex] = weight;}} else if (refIndex == index && !lowCost[i].equals(visitedVal) &&weight.compareTo(lowCost[i]) < 0) {if (!reverseAdjacency) {// 指向本顶点的tailVex[i] = i;headVex[i] = refIndex;lowCost[i] = weight;} else {tailVex[i] = refIndex;headVex[i] = i;lowCost[i] = weight;}}edgeNode = edgeNode.getNext();}}// 取lowCost中最小的那个W minWeight = null;for (int i = 0; i < vertexNum; i++) {// 忽略自身// 忽略lowCost[j]为已访问过的顶点if (i != index && !lowCost[i].equals(visitedVal)) {if (null == minWeight || minWeight.compareTo(lowCost[i]) > 0) {minWeight = lowCost[i];index = i;}}}// 打印取到的边switch (type) {case DIRECTED_NETWORK: {String val = "<" + tailVex[index] + "," + headVex[index] + ">";result.add(val);// 用于测试System.out.println(val);break;}case UNDIRECTED_NETWORK: {String val = "(" + tailVex[index] + "," + headVex[index] + ")";result.add(val);// 用于测试System.out.println(val);break;}}// 设置已连通的顶点数if (!visited[tailVex[index]]) {visited[tailVex[index]] = true;connectedNum++;}// 设置该顶点已处理if (!visited[headVex[index]]) {visited[headVex[index]] = true;connectedNum++;}// 设置lowCost[index]为已访问lowCost[tailVex[index]] = visitedVal;lowCost[headVex[index]] = visitedVal;// 用于测试StringBuilder builder = new StringBuilder("lowCost is [");StringBuilder builder2 = new StringBuilder("tailVex is [");StringBuilder builder3 = new StringBuilder("headVex is [");for (int i = 0; i < vertexNum; i++) {builder.append(lowCost[i]).append(",");builder2.append(tailVex[i]).append(",");builder3.append(headVex[i]).append(",");}builder.append("]");builder2.append("]");System.out.println(builder);System.out.println(builder2);System.out.println(builder3);}return result;}
5.1.3 十字链表的最小生成树
十字链表记录了每个顶点的in和out,因此十字链表的处理较为简单。
/*** 生成最小生成树** @param visitedVal 已访问的顶点被标记的值* @return 最小生成树的边或弧列表* @author Korbin* @date 2023-02-07 15:23:14**/
@SuppressWarnings("unchecked")
public List<String> minimumCostSpanningTree(W visitedVal) {List<String> result = new ArrayList<>();if (type.equals(BusinessConstants.GRAPH_TYPE.UNDIRECTED) ||type.equals(BusinessConstants.GRAPH_TYPE.DIRECTED)) {// 最小生成树只针对网return null;}// 用于存储“当前检查的顶点X与顶点j的权W(X,j)”及“顶点adjVex[j]到顶点j的权W(adj[j],j)”中较优(如果是数值的话就是较小)的那个权W[] lowCost = (W[]) Array.newInstance(infinity.getClass(), vertexNum);for (int i = 0; i < vertexNum; i++) {lowCost[i] = infinity;}// 用于存储箭头的尾和头int[] tailVex = new int[vertexNum];int[] headVex = new int[vertexNum];boolean[] visited = new boolean[vertexNum];int connectedNum = 0;int index = 0;while (connectedNum < vertexNum) {AcrossLinkVertexNode<T, W> vertexNode = vertexes[index];// 处理指向自己的AcrossLinkEdgeNode<W> inEdge = vertexNode.getFirstIn();while (null != inEdge) {// 自身是headint tailIndex = inEdge.getTailIndex();W weight = inEdge.getWeight();if (!lowCost[tailIndex].equals(visitedVal) && weight.compareTo(lowCost[tailIndex]) < 0) {lowCost[tailIndex] = weight;tailVex[tailIndex] = tailIndex;headVex[tailIndex] = index;}inEdge = inEdge.getNextTail();}// 处理指向的AcrossLinkEdgeNode<W> outEdge = vertexNode.getFirstOut();while (null != outEdge) {// 自身是tailint headIndex = outEdge.getHeadIndex();W weight = outEdge.getWeight();if (!lowCost[headIndex].equals(visitedVal) && weight.compareTo(lowCost[headIndex]) < 0) {lowCost[headIndex] = weight;tailVex[headIndex] = index;headVex[headIndex] = headIndex;}outEdge = outEdge.getNextHead();}// 取lowCost中最小的那个W minWeight = null;for (int i = 0; i < vertexNum; i++) {// 忽略自身// 忽略lowCost[j]为已访问过的顶点if (i != index && !lowCost[i].equals(visitedVal)) {if (null == minWeight || minWeight.compareTo(lowCost[i]) > 0) {minWeight = lowCost[i];index = i;}}}// 打印取到的边switch (type) {case DIRECTED_NETWORK: {String val = "<" + tailVex[index] + "," + headVex[index] + ">";result.add(val);// 用于测试System.out.println(val);break;}case UNDIRECTED_NETWORK: {String val = "(" + tailVex[index] + "," + headVex[index] + ")";result.add(val);// 用于测试System.out.println(val);break;}}// 设置已连通的顶点数if (!visited[tailVex[index]]) {visited[tailVex[index]] = true;connectedNum++;}// 设置该顶点已处理if (!visited[headVex[index]]) {visited[headVex[index]] = true;connectedNum++;}// 设置lowCost[index]为已访问lowCost[tailVex[index]] = visitedVal;lowCost[headVex[index]] = visitedVal;// 用于测试StringBuilder builder = new StringBuilder("lowCost is [");StringBuilder builder2 = new StringBuilder("tailVex is [");StringBuilder builder3 = new StringBuilder("headVex is [");for (int i = 0; i < vertexNum; i++) {builder.append(lowCost[i]).append(",");builder2.append(tailVex[i]).append(",");builder3.append(headVex[i]).append(",");}builder.append("]");builder2.append("]");System.out.println(builder);System.out.println(builder2);System.out.println(builder3);}return result;}
5.1.4 邻接多重表的最小生成树
邻接多重表是对无向网的优化,因此我们不考虑有向网,而在无向网中,通过iVex、iLink、jVex、jLink,可以直接定位到某顶点关联的所有顶点,因此代码实现如下所示:
/*** 生成最小生成树** @param visitedVal 已访问的顶点被标记的值* @return 最小生成树的边或弧列表* @author Korbin* @date 2023-02-07 15:23:14**/
@SuppressWarnings("unchecked")
public List<String> minimumCostSpanningTree(W visitedVal) {List<String> result = new ArrayList<>();if (type.equals(BusinessConstants.GRAPH_TYPE.UNDIRECTED) ||type.equals(BusinessConstants.GRAPH_TYPE.DIRECTED) ||type.equals(BusinessConstants.GRAPH_TYPE.DIRECTED_NETWORK)) {// 最小生成树只针对无向网return null;}// 用于存储“当前检查的顶点X与顶点j的权W(X,j)”及“顶点adjVex[j]到顶点j的权W(adj[j],j)”中较优(如果是数值的话就是较小)的那个权W[] lowCost = (W[]) Array.newInstance(infinity.getClass(), vertexNum);for (int i = 0; i < vertexNum; i++) {lowCost[i] = infinity;}// 用于存储箭头的尾和头int[] tailVex = new int[vertexNum];int[] headVex = new int[vertexNum];boolean[] visited = new boolean[vertexNum];int connectedNum = 0;int index = 0;while (connectedNum < vertexNum) {AdjacencyMultiVertexNode<T, W> vertexNode = vertexes[index];AdjacencyMultiEdgeNode<W> edgeNode = vertexNode.getFirstEdge();boolean firstEdge = true;while (null != edgeNode) {int refIndex = index;int iVex = edgeNode.getIVex();int jVex = edgeNode.getJVex();W weight = edgeNode.getWeight();if (firstEdge) {refIndex = jVex;edgeNode = edgeNode.getILink();firstEdge = false;} else {if (iVex == index) {refIndex = jVex;} else if (jVex == index) {refIndex = iVex;}edgeNode = edgeNode.getJLink();}if (!lowCost[refIndex].equals(visitedVal) && weight.compareTo(lowCost[refIndex]) < 0) {lowCost[refIndex] = weight;tailVex[refIndex] = iVex;headVex[refIndex] = jVex;}}// 取lowCost中最小的那个W minWeight = null;for (int i = 0; i < vertexNum; i++) {// 忽略自身// 忽略lowCost[j]为已访问过的顶点if (i != index && !lowCost[i].equals(visitedVal)) {if (null == minWeight || minWeight.compareTo(lowCost[i]) > 0) {minWeight = lowCost[i];index = i;}}}// 打印取到的边switch (type) {case DIRECTED_NETWORK: {String val = "<" + tailVex[index] + "," + headVex[index] + ">";result.add(val);// 用于测试System.out.println(val);break;}case UNDIRECTED_NETWORK: {String val = "(" + tailVex[index] + "," + headVex[index] + ")";result.add(val);// 用于测试System.out.println(val);break;}}// 设置已连通的顶点数if (!visited[tailVex[index]]) {visited[tailVex[index]] = true;connectedNum++;}// 设置该顶点已处理if (!visited[headVex[index]]) {visited[headVex[index]] = true;connectedNum++;}// 设置lowCost[index]为已访问lowCost[tailVex[index]] = visitedVal;lowCost[headVex[index]] = visitedVal;// 用于测试StringBuilder builder = new StringBuilder("lowCost is [");StringBuilder builder2 = new StringBuilder("tailVex is [");StringBuilder builder3 = new StringBuilder("headVex is [");for (int i = 0; i < vertexNum; i++) {builder.append(lowCost[i]).append(",");builder2.append(tailVex[i]).append(",");builder3.append(headVex[i]).append(",");}builder.append("]");builder2.append("]");System.out.println(builder);System.out.println(builder2);System.out.println(builder3);}return result;}
5.5.5 边集数组的最小生成树
边集数组的最小生成树实现代码如下所示:
/*** 生成最小生成树** @param visitedVal 已访问的顶点被标记的值* @return 最小生成树的边或弧列表* @author Korbin* @date 2023-02-07 15:23:14**/
@SuppressWarnings("unchecked")
public List<String> minimumCostSpanningTree(W visitedVal) {List<String> result = new ArrayList<>();if (type.equals(BusinessConstants.GRAPH_TYPE.UNDIRECTED) ||type.equals(BusinessConstants.GRAPH_TYPE.DIRECTED)) {// 最小生成树只针对网return null;}// 用于存储“当前检查的顶点X与顶点j的权W(X,j)”及“顶点adjVex[j]到顶点j的权W(adj[j],j)”中较优(如果是数值的话就是较小)的那个权W[] lowCost = (W[]) Array.newInstance(infinity.getClass(), vertexNum);for (int i = 0; i < vertexNum; i++) {lowCost[i] = infinity;}// 用于存储箭头的尾和头int[] tailVex = new int[vertexNum];int[] headVex = new int[vertexNum];boolean[] visited = new boolean[vertexNum];int connectedNum = 0;int index = 0;while (connectedNum < vertexNum) {for (int i = 0; i < edgeNum; i++) {EdgeListEdgeNode<W> edgeNode = arc[i];int begin = edgeNode.getBegin();int end = edgeNode.getEnd();W weight = edgeNode.getWeight();if (begin == index && !lowCost[end].equals(visitedVal) && weight.compareTo(lowCost[end]) < 0) {lowCost[end] = weight;tailVex[end] = begin;headVex[end] = end;} else if (end == index && !lowCost[begin].equals(visitedVal) && weight.compareTo(lowCost[begin]) < 0) {lowCost[begin] = weight;tailVex[begin] = begin;headVex[begin] = end;}}// 取lowCost中最小的那个W minWeight = null;for (int i = 0; i < vertexNum; i++) {// 忽略自身// 忽略lowCost[j]为已访问过的顶点if (i != index && !lowCost[i].equals(visitedVal)) {if (null == minWeight || minWeight.compareTo(lowCost[i]) > 0) {minWeight = lowCost[i];index = i;}}}// 打印取到的边switch (type) {case DIRECTED_NETWORK: {String val = "<" + tailVex[index] + "," + headVex[index] + ">";result.add(val);// 用于测试System.out.println(val);break;}case UNDIRECTED_NETWORK: {String val = "(" + tailVex[index] + "," + headVex[index] + ")";result.add(val);// 用于测试System.out.println(val);break;}}// 设置已连通的顶点数if (!visited[tailVex[index]]) {visited[tailVex[index]] = true;connectedNum++;}// 设置该顶点已处理if (!visited[headVex[index]]) {visited[headVex[index]] = true;connectedNum++;}// 设置lowCost[index]为已访问lowCost[tailVex[index]] = visitedVal;lowCost[headVex[index]] = visitedVal;// 用于测试StringBuilder builder = new StringBuilder("lowCost is [");StringBuilder builder2 = new StringBuilder("tailVex is [");StringBuilder builder3 = new StringBuilder("headVex is [");for (int i = 0; i < vertexNum; i++) {builder.append(lowCost[i]).append(",");builder2.append(tailVex[i]).append(",");builder3.append(headVex[i]).append(",");}builder.append("]");builder2.append("]");System.out.println(builder);System.out.println(builder2);System.out.println(builder3);}return result;}
5.2 克鲁斯卡尔(Kruskal)算法
克鲁斯卡尔的官方描述是“假设N=(V,{E})是连通网,则令最小生成树的初始状态为只有n个顶点而无边的非连通图T=(V,{}),图中每个顶点自成一个连通分量。在E中选择代价最小的边,若该边依附的顶点落在T中不同的连通分量上,则将此边加入到T中,否则舍去此边选择下一条代价最小的边。依此类推,直到T中所有顶点都在同一连通分量上为止”。
克鲁斯卡尔算法针对的是边,因此我们用边集数组来进行克鲁斯卡尔算法的实现描述,以以下边集数组为例:
首先我们定义一个数组connected来存储已连通的分量,长度为顶点长度,默认值均为无穷大,表示所有顶点均为连通:
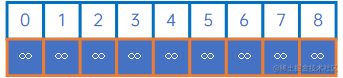
这里面的规则是:如果connected[i]=j,connected[j]=x,connected[x]=∞\infty∞,则表示顶点i、j、x是连通的。
然后我们把边集数组按权由小到大排序:
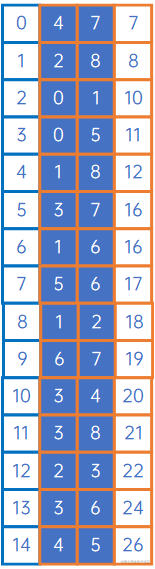
迭代边集数组,首先是arc[0],begin=4,end=7,connected[4]=∞\infty∞,connected[7]=∞\infty∞,这两个顶点未连通,我们把它们连通起来,输出第一个连通分量的第一条边(4,7),同时令connected[4]=7,表示这两个顶点已连通:

然后是arc[1],begin=2,end=8,connected[2]=∞\infty∞,connected[8]=∞\infty∞,这两个顶点未连通,我们把它们连通起来,输出第二个连通分量的第一条边(2,8),同时令connected[2]=8,表示这两个顶点已连通:

后续arc[2]处理方式同上:

然后看arc[3],begin=0,end=5,注意到,connected[0]=1,表示第0和第1个顶点是已经连通的,第0个顶点已在一个连通分量内,我们继续看这个连通分量里面有哪些顶点:connected[0]=1,connected[1]=∞\infty∞,按上面定的规则,表示这个连通分量里面只有0和1两个顶点;connected[5]=∞\infty∞,表示顶点5没有在任何一个连通分量内,这时,我们令connected[1]=5,表示顶点0、1、5在同一个连通分量内,并输出(0,5),表示这个边是这个连通分量的一条边:

然后看arc[4],begin=1,end=8,因connected[1]=5,connected[5]=0,connected[8]=∞\infty∞,表示顶点1和顶点5在同一个连通分量内,但这个连通分量不包含顶点8,因此令connected[5]=8,并输出边(1,8),将顶点8也加入到这个连通分量内:

接下来arc[5]和arc[6]的处理方式类似:

来看arc[7],begin=5,end=6,此时,connected[5]=8,connected[8]=6,connected[6]=0,即顶点5、8、6在一个连通分量内,即begin和end都在一个连通分量内,不需要处理,跳过。
arc[8]与arc[7]一致,相关顶点都在同一个连通分量内,不需要处理,跳过。
继续迭代arc,按如上规则处理,能得到最终的最小生成树。
代码实现如下所示:
/*** 生成最小生成树,克鲁斯卡尔算法** @return 最小生成树的边或弧列表* @author Korbin* @date 2023-02-13 15:09:58**/
public List<String> minimumCostSpanningTree() {List<String> result = new ArrayList<>();if (type.equals(BusinessConstants.GRAPH_TYPE.UNDIRECTED) ||type.equals(BusinessConstants.GRAPH_TYPE.DIRECTED)) {// 最小生成树只针对网return null;}// 对边集数组按权从小到大进行排序sortArc(0, edgeNum);// 定义一个数组,并初始化为infinity,用于表示连通分量int[] connected = new int[vertexNum];for (int i = 0; i < vertexNum; i++) {connected[i] = -1;}// 迭代边集数组for (int i = 0; i < edgeNum; i++) {EdgeListEdgeNode<W> edgeNode = arc[i];int begin = edgeNode.getBegin();int end = edgeNode.getEnd();// 寻找begin对应的连通分量int beginComponent = begin;while (connected[beginComponent] != -1) {beginComponent = connected[beginComponent];}// 寻找end对应的连通分量int endComponent = end;while (connected[endComponent] != -1) {endComponent = connected[endComponent];}// 如果不在同一个连通分量if (beginComponent != endComponent) {connected[beginComponent] = end;switch (type) {case UNDIRECTED_NETWORK: {String val = "(" + begin + "," + end + ")";result.add(val);break;}case DIRECTED_NETWORK: {String val = "<" + begin + "," + end + ">";result.add(val);break;}}}}return result;
}
5.3 总结
普里姆(Prim)算法,从一个顶点出发X,取其他所有顶点与X连通的权中最小权对应的那个顶点Y,放入连通分量TE中,然后取其他所有顶点与X和Y连通的权中最小权对应的那个顶点Z,放入连通分量中,直到所有的顶点都在连通分量中时,最小生成树生成。
克鲁斯卡尔(Kruskal)算法,把所有的边放到一个数组中,按权从小到大排序,然后从第一条边开始迭代,判断begin和end是否在同一个连通分量,若不在,则把他们连通起来,直到所有边都处理完毕。
相对来讲,克鲁斯卡算法更适用于边集数组,而普里姆虽然各类存储结构都可以实现,但时间复杂度不同:
| 存储结构 | 普里姆算法 | 克鲁斯卡尔算法 | ||
|---|---|---|---|---|
| 适用性 | 最差时间复杂度 | 适用性 | 最差时间复杂度 | |
| 邻接矩阵 | 适用 | O(n2) | 不适用 | -- |
| 邻接表 | 适用 | O(n3) | 不适用 | -- |
| 十字链表 | 适用 | O(n2) | 不适用 | -- |
| 邻接多重表 | 适用 | O(n2) | 不适用 | -- |
| 边集数组 | 适用 | O(n2) | 适用 | O(nlog(n)) |
注:本文为程 杰老师《大话数据结构》的读书笔记,其中一些示例和代码是笔者阅读后自行编制的。
相关文章:

大话数据结构-普里姆算法(Prim)和克鲁斯卡尔算法(Kruskal)
5 最小生成树 构造连通网的最小代价生成树称为最小生成树,即Minimum Cost Spanning Tree,最小生成树通常是基于无向网/有向网构造的。 找连通网的最小生成树,经典的有两种算法,普里姆算法和克鲁斯卡尔算法。 5.1 普里姆ÿ…...
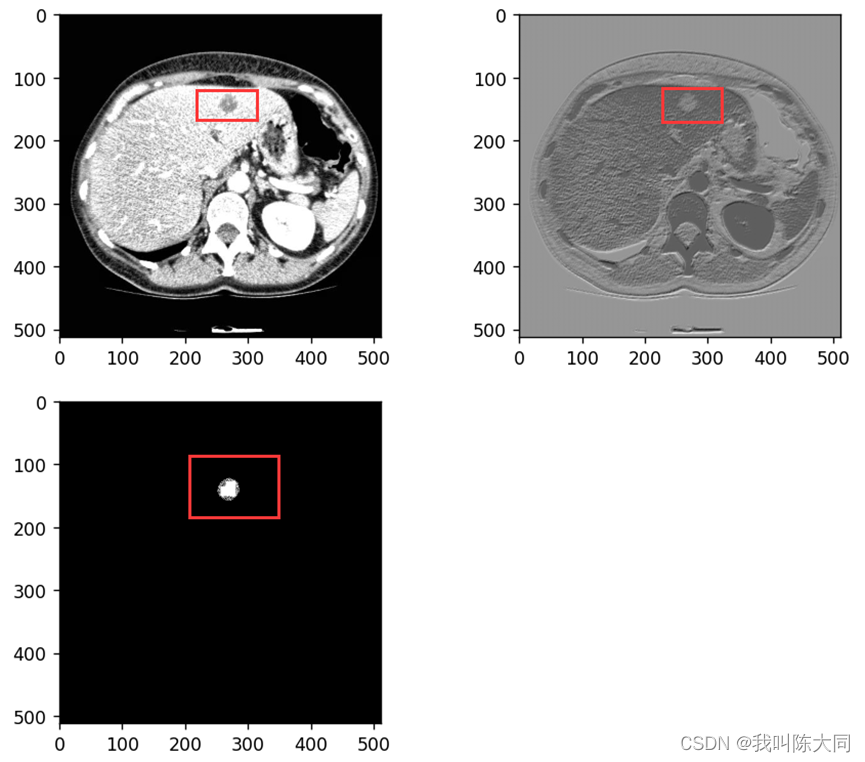
UNet-肝脏肿瘤图像语义分割
目录 一. 语义分割 二. 数据集 三. 数据增强 图像数据处理步骤 CT图像增强方法 :windowing方法 直方图均衡化 获取掩膜图像深度 在肿瘤CT图中提取肿瘤 保存肿瘤数据 四. 数据加载 数据批处理 编辑编辑 数据集加载 五. UNet神经网络模型搭建 单张图片…...

三周爆赚千万 电竞选手在无聊猿游戏赢麻了
如何用3个星期赚到1千万?普通人做梦都不敢想的事,电竞职业选手Mongraal却用几把游戏轻易完成,赚钱地点是蓝筹NFT项目Bored Ape Yacht Club(BAYC无聊猿)出品的新游戏Dookey Dash。 这款游戏类似《神庙逃亡》࿰…...

BERT学习
非精读BERT-b站有讲解视频(跟着李沐学AI) (大佬好厉害,讲的比直接看论文容易懂得多) 写在前面 在计算MLM预训练任务的损失函数的时候,参与计算的Tokens有哪些?是全部的15%的词汇还是15%词汇中真…...
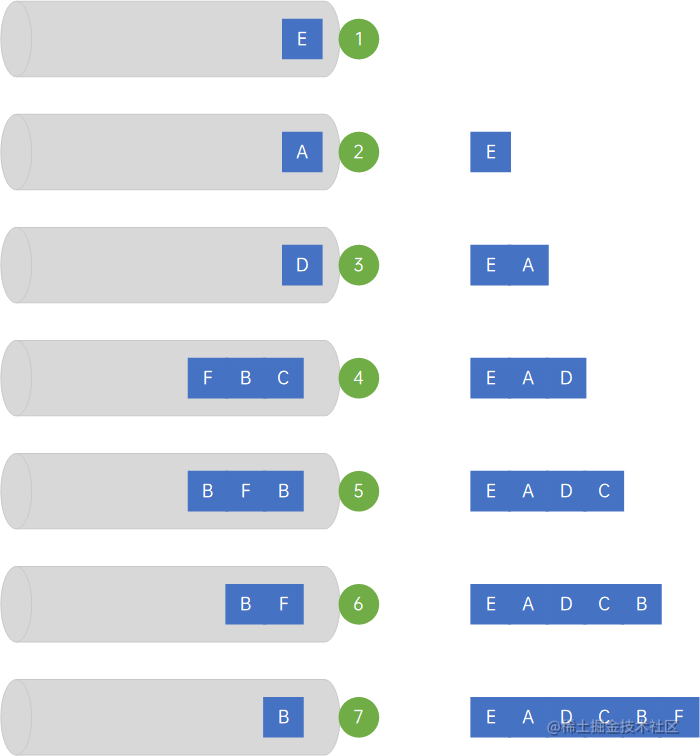
大话数据结构-图的深度优先遍历和广度优先遍历
4 图的遍历 图的遍历分为深度优先遍历和广度优先遍历两种。 4.1 深度优先遍历 深度优先遍历(Depth First Search),也称为深度优先搜索,简称DFS,深度优先遍历,是指从某一个顶点开始,按照一定的规…...

c语言指针怎么理解 第一部分
不理解指针,是因为有人教错了你。 有人告诉你,指针是“指向”某某某的,那就是误导你,给你挖了个坑。初学者小心不要误读这“指向”二字。 第一,“指针”通常用于保存一个地址,这个地址的数据类型在定义指…...
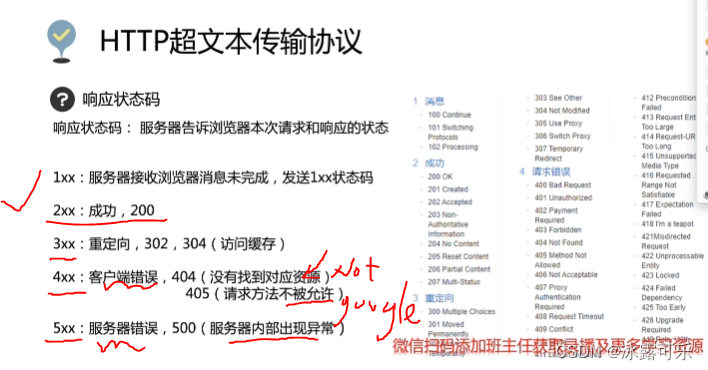
计算机网络安全基础知识2:http超文本传输协议,请求request消息的get和post,响应response消息的格式,响应状态码
计算机网络安全基础知识: 2022找工作是学历、能力和运气的超强结合体,遇到寒冬,大厂不招人,可能很多算法学生都得去找开发,测开 测开的话,你就得学数据库,sql,oracle,尤…...

Pytest自动化框架~权威教程03-原有TestSuite的执行方法
前言TestSuite一直是unittest的灵活与精髓之处, 在繁多的测试用例中, 可以任意挑选和组合各种用例集, 比如smoke用例集, level1用例集, webtest用例集, bug回归用例集等等, 当然这些TestSuite需要我们提前定义好, 并把用例加载进去.Pytest采取的是完全不同的用例组织和运行方式…...

web自动化 基于python+Selenium+PHP+Ftp实现的轻量级web自动化测试框架
1、 开发环境 win7 64 PyCharm 4.0.5 setuptools-29.0.1.zip 下载地址:setuptools-29.0.1.zip_免费高速下载|百度网盘-分享无限制 官方下载地址:setuptools PyPI python 3.3.2 mysql-connector-python-2.1.4-py3.3-win64 下载地址:mysq…...

【MyBatis】源码学习 05 - 关于 xml 文件解析的分析
文章目录前言参考目录学习笔记1、章节目录概览2、14.3:SqlSourceBuilder 类与 StaticSqlSource 类3、14.4.2:ResultMapResolver 类3.1、测试代码说明3.2、结果集 userMap 解析流程3.3、结果集 getGirl 解析流程3.4、鉴别器 discriminator 解析流程4、14.…...
代码随想录算法训练营第二天| 977. 有序数组的平方、209. 长度最小子数组、59.螺旋矩阵II
977 有序数组的平方题目链接:977 有序数组的平方介绍给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。思路看到题目的第一反应,首先负数的平方跟正数的平方是相同的&…...
Ethercat系列(10)用QT实现SOEM主站
首先将SOEM编译成静态Lib库可以参考前面的博文(83条消息) VS2017下编译SOEM(Simle Open EtherCAT Master)_soem vs_CoderIsArt的博客-CSDN博客make_libsoem_lib.bat "C:\Program Files (x86)\Microsoft Visual Studio\2017\Community\VC\Auxiliary\Build" x86用QT创建…...

论文投稿指南——中文核心期刊推荐(科学、科学研究)
【前言】 🚀 想发论文怎么办?手把手教你论文如何投稿!那么,首先要搞懂投稿目标——论文期刊 🎄 在期刊论文的分布中,存在一种普遍现象:即对于某一特定的学科或专业来说,少数期刊所含…...
、attr()和data())
jQuery属性操作prop()、attr()和data()
jQuery 提供了一些属性操作的方法,主要包括 prop()、attr() 和 data() 等。通过这些方法,能够实现不同的需求。下面我们分别进行详细讲解。 1.prop() 方法 prop0 方法用来设置或获取元素固有属性值。元素固有属性是指元素本身自带的属性,如 …...
git的使用
1.git的四个区域: 2.常规git命令 git status 查看working directory哪些文件被更改了git add .把更改add到staging area,缓存的地方。改一个地方可以就先暂存一下,最后确认是哪些改动后再一起commit,以免不必要的版本。 在暂存区域ÿ…...
webpack生产环境配置
3 webpack生产环境配置 由于笔记文档没有按照之前的md格式书写,所以排版上代码上存在问题😢😢😢😢 09 提取css成单独文件 使用下载插件 npm i mini-css-extract-plugin0.9.0 -D webpack配置此时a,b提取成单独文件,并且…...
linux下安装jenkins
1.初始化Jenkins安装环境 系统版本:Red Hat Enterprise Linux 8.7 将脚本文件jenkins_install_env.sh 、 jenkins_install.sh和apache-maven-3.6.2-bin.tar.gz、jdk-8u251-linux-x64.tar.gz都上传到/usr/local/src目录下执行jenkins_install_env.sh脚本初始化Jenki…...

IGKBoard(imx6ull)-I2C接口编程之SHT20温湿度采样
文章目录1- 使能开发板I2C通信接口2- SHT20硬件连接3- 编码实现SHT20温湿度采样思路(1)查看sht20从设备地址(i2cdetect)(2)获取数据大体流程【1】软复位【2】触发测量与通讯时序(3)返…...
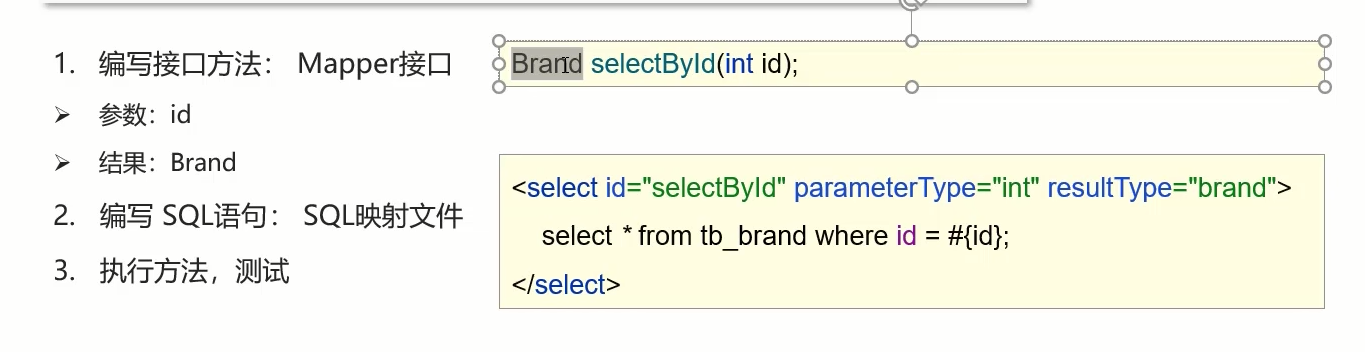
MyBatis——配置文件完成增删改查
1.首先先创建一个新的表,使用下面的sql语句 -- 删除tb_brand表 drop table if exists tb_brand; -- 创建tb_brand表 create table tb_brand (-- id 主键id int primary key auto_increment,-- 品牌名称brand_name varchar(20),-- 企业名称company_name varchar(20…...

Python内置函数 — all,any
1、all 源码注释: def all(*args, **kwargs): # real signature unknown"""Return True if bool(x) is True for all values x in the iterable.If the iterable is empty, return True."""pass 语法格式: all(iterable)…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...
