非线性约束的优化问题_序列二次规划算法代码
1. 理论部分
2. 序列二次规划算法代码及解析
3.完整代码
1.理论部分
a.约束优化问题的极值条件
库恩塔克条件(Kuhn-Tucker conditions,KT条件)是确定某点为极值点的必要条件。如果所讨论的规划是凸规划,那么库恩-塔克条件也是充分条件。
(1)判断数值x处起作用的约束,计算x处各约束的取值是否为0,找出起作用的约束条件。并非所有约束条件都起作用,即并非落在所有约束条件的边界交集处。对于起作用的边界条件,满足边界函数g(x)或h(x)为0;
(2)数值x处,目标函数导数f'(x)和起作用的约束导数g'(x)的数值;
(3)代入KT条件(ex. ),求解拉格朗日乘子λ的大小,判断λ是否大于0,若大于零,则为极值点。
(4)若不满足条件,继续迭代。
具体做法如下:

其中λ为拉格朗日乘子,当某一点x使λ > 0存在时,称满足KT条件,则该点x是极值点。
约束优化问题的应用示例如下图:

b.约束优化方法及迭代
此处介绍和使用外惩罚函数法/外点法
外点法是一种从随机一点(一般在可行域外)出发,逐渐移动到可行区域的方法。
对于约束优化问题:
构造外惩罚函数:
即,当g(x)不满足条件时,该项有大于0的值,h(x)不满足条件时,该项也有值,加和的越大代表该数值点距离距离约束的可行域越远,惩罚项的值越大,惩罚作用越明显。。其中Mk为外罚因子,M 0 < M 1 < M 2 . . . < M k 为递增的正数序列,一般M0=1,递增系数c=5~8。
迭代终止满足两个判断条件中一个即可:
1. ,Q为当前数值点多个约束函数中最大的值,即满足了所有的约束函数条件。
2. 且
,R为外罚因子控制量,M超出外罚因子的极限R
外点法的迭代图如下:
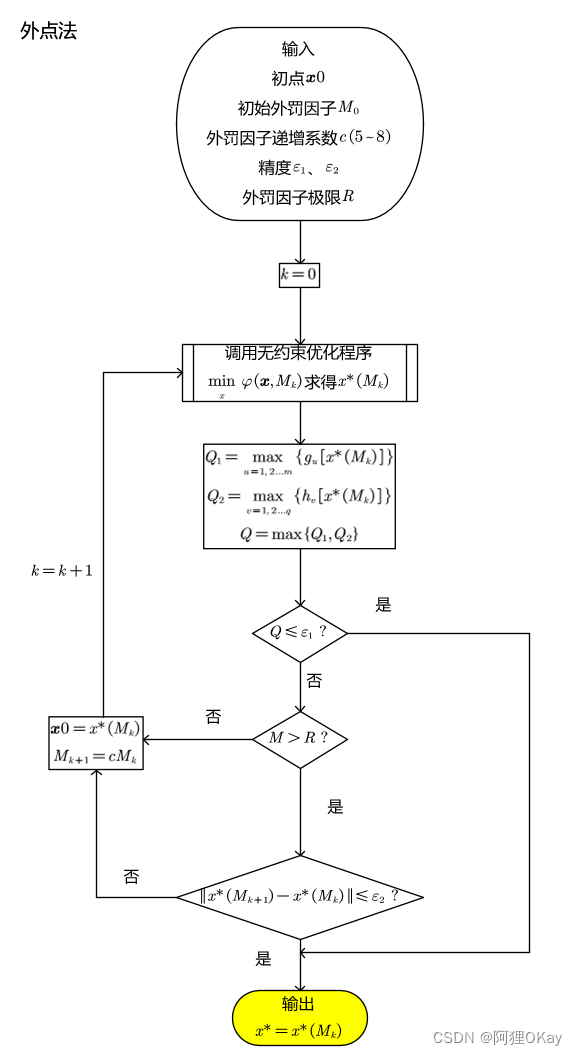
外点法的示例如下图:

a. 定义变量
vars = 2; % 自变量数量
cons = 1; % 约束数量
maxIter=100; % 最大迭代次数
x = [-1;4]; % 初始猜测值
l =0; % 拉格朗日乘子
H = eye(vars,vars); % Hessian 矩阵,假设为I矩阵目标函数为
及目标函数的导数为
function y = f(x)y = x(1)^4 - 2*x(2)*x(1)^2 + x(2)^2 + x(1)^2 - 2*x(1)+5;
endfunction y = gradf(x)y(1) = 2*x(1)-4*x(1)*x(2)+4*x(1)^3-2;y(2) = -2*x(1)^2 + 2*x(2);
end约束项不等式为
以及其导数为
function y = g(x)y(1) = -(x(1)+0.25)^2+0.75*x(2);
endfunction y = gradg(x)y(1,1) = -2*x(1)-1/2;y(1,2) = 3/4;
end求解KKT条件
function y = SolveKKT(gradfEval,gradgEval,gEval,Hessian)A = [Hessian -gradgEval';gradgEval 0]; %对称矩阵,约束函数的梯度矩阵b = [-gradfEval -gEval]';y = A\b; %方程 Ay = b 解出y值,分别对应最优的x值的梯度和最优的拉格朗日乘子的值%即此时Ay-b = 0,kkt条件成立,
end判断数值点x是否满足约束条件
function [gViol,lViol] = Viols(gEval,l)%约束条件函数值,拉格朗日乘子lgViol=[];lViol=[];for i = 1:length(gEval)if gEval(i)<0 %如果约束条件函数值小于零,即,不满足约束条件gViol(i)=gEval(i); %将约束条件函数值和拉格朗日乘子l,放入列表lViol(i)=l(i);end end
end处理不满足约束的情况,构造惩罚函数,lViol对应Mk,累加得到惩罚函数
function y = Penalty(fEval,gViol,lViol)
%代入该点处的函数值,不满足约束的约束函数值,以及拉格朗日乘子lsum = 0;y = fEval;for i = 1:length(gViol) %找出不满足约束条件的约束函数值sum = sum + lViol(i)*abs(gViol(i)); %约束函数值g(x)求反,再乘一个系数,即,||l_1*g(x1)+l2*g(x2) ||endy = y + sum;
end在初始点首先进行初始计算,找出不满足约束的约束,计算其损失函数。
% EVALUATE AT STARTING POINTfEval= f(x);
gEval = g(x);
[gViol,lViol] = Viols(gEval,l);
gradfEval = gradf(x);
gradgEval = gradg(x);
P = Penalty(fEval,gViol,lViol);开始进入SQP算法主体,求解kkt条件,得到xSol为函数x的解,lSol为拉格朗日乘子的解。
for i=1:maxIter %开始循环迭代% SOLVE KKT CONDITIONS FOR THE OPTIMUM OF THE QUADRATIC APPROXIMATION%求解二次优化的KKT条件sol = SolveKKT(gradfEval,gradgEval,gEval,H);%代入导数f'(x),g'(x),约束函数值g(x),Hessian矩阵,xSol = sol(1:vars);lSol = sol(vars+1:vars+cons);如果拉格朗日乘子有负的,即,不满足约束条件,则将其设为0,并重新求解方程
for j = 1:length(lSol)if lSol(j)<0 %如果拉格朗日乘子有一个是负的sol= H\(-gradfEval)'; %将结果重新求解H*x = -gradfEvalxSol = sol(1:vars);lSol(j)=0; %该约束的拉格朗日乘子置为0endend计算新的数值点情况
xNew = x + xSol; %更新得到新的数值点lNew = lSol; % 得到新的拉格朗日乘子fEvalNew = f(xNew);%计算新点目标函数的数值gEvalNew = g(xNew);%计算新点的约束函数数值gradfEvalNew = gradf(xNew);%计算该点目标函数梯度gradgEvalNew = gradg(xNew);%计算该点约束函数梯度[gViolNew,lViolNew] = Viols(gEvalNew,lNew);%找出不满足的约束条件PNew = Penalty(fEvalNew,gViolNew,lViolNew);%求解惩罚函数如果惩罚函数增加,减小步长到原来的一半
% IF PENALTY FUNCTION INCREASED, LOWER THE STEP BY 0.5while PNew-P>1e-4xSol = 0.5*xSol;xNew = x + xSol;fEvalNew = f(xNew);gEvalNew = g(xNew);gradfEvalNew = gradf(xNew);gradgEvalNew = gradg(xNew);[gViolNew,lViolNew] = Viols(gEvalNew,lNew);PNew = Penalty(fEvalNew,gViolNew,lViolNew);end如果x数值变化很小,停止迭代,找到最优,结束迭代
% STOPPING CRITERIONif norm(xNew(1:vars)-x(1:vars))<=1e-2breakend更新Hessian矩阵,Q为Mk+1- Mk的值
% UPDATE THE HESSIANgradLEval = gradLagr(gradfEval,gradgEval,lNew,vars); %拉格朗日函数的梯度 lnew not l!!!gradLEvalNew = gradLagr(gradfEvalNew,gradgEvalNew,lNew,vars);%新的数值点处,拉格朗日函数的梯度Q = gradLEvalNew-gradLEval;%拉格朗日函数数值的差分L(x_k+1) - L(x_k)dx = xNew-x;%自变量x的差分HNew = UpdateH(H,dx,Q);%求解H矩阵计算拉格朗日乘子梯度的函数
function y = gradLagr(gradfEval,gradgEval,l,n)y = gradfEval';sum = zeros(n,1);for i = 1:length(l)sum = sum -l(i)*gradgEval(i:n)';endy = y + sum; %x处目标函数的梯度,减去约束函数的梯度。即,拉格朗日函数的梯度
end更新Hessian矩阵,gamma为Mk+1- Mk的值
function y = UpdateH(H,dx,gamma)%gamma是拉格朗日函数的两次差分term1=(gamma*gamma') / (gamma'*dx);term2 = ((H*dx)*(dx'*H)) / (dx'*(H*dx));y = H + term1-term2; %更新得到新的H矩阵
end更新所有的变量,用于下次的迭代,包括Hessian矩阵H,数值点x,惩罚函数值P,目标函数值fEval,目标函数值梯度gradEval,约束函数值gEval,约束函数值梯度gradgEval
% UPDATE ALL VALUES FOR NEXT ITERATIONH = HNew;fEval = fEvalNew;gEval = gEvalNew;gradfEval = gradfEvalNew;gradgEval = gradgEvalNew;P = PNew;x = xNew;3.可以运行的完整代码如下:
% EXAMPLE OF SQP ALGORITHMclear variables; close all; clc;
fprintf("---------------------------------------------------------------\n")
fprintf("An implementation of Sequential Quadratic Programming method\nin a nonlinear constrained optimization problem\n")
fprintf("---------------------------------------------------------------\n")% INITIAL VALUES - INPUTvars = 2; % number of variables
cons = 1; % number of constraints
maxIter=100; % max iterations
x = [-1;4]; % initial guess point
l =0; % LagrangeMultipliers vector
H = eye(vars,vars); % Hessian matrix assumed to be identity% EVALUATE AT STARTING POINTfEval= f(x);
gEval = g(x);
[gViol,lViol] = Viols(gEval,l);
gradfEval = gradf(x);
gradgEval = gradg(x);
P = Penalty(fEval,gViol,lViol);% SQP ALGORITHMfor i=1:maxIter% SOLVE KKT CONDITIONS FOR THE OPTIMUM OF THE QUADRATIC APPROXIMATIONsol = SolveKKT(gradfEval,gradgEval,gEval,H);xSol = sol(1:vars);lSol = sol(vars+1:vars+cons);% IF THE LAGRANGE MULTIPLIER IS NEGATIVE SET IT TO ZEROfor j = 1:length(lSol)if lSol(j)<0 sol= H\(-gradfEval)';xSol = sol(1:vars);lSol(j)=0;endend% EVALUATE AT NEW CANDIDATE POINTxNew = x + xSol; lNew = lSol;fEvalNew = f(xNew);gEvalNew = g(xNew);gradfEvalNew = gradf(xNew);gradgEvalNew = gradg(xNew);[gViolNew,lViolNew] = Viols(gEvalNew,lNew);PNew = Penalty(fEvalNew,gViolNew,lViolNew);% IF PENALTY FUNCTION INCREASED, LOWER THE STEP BY 0.5while PNew-P>1e-4xSol = 0.5*xSol;xNew = x + xSol;fEvalNew = f(xNew);gEvalNew = g(xNew);gradfEvalNew = gradf(xNew);gradgEvalNew = gradg(xNew);[gViolNew,lViolNew] = Viols(gEvalNew,lNew);PNew = Penalty(fEvalNew,gViolNew,lViolNew);end% STOPPING CRITERIONif norm(xNew(1:vars)-x(1:vars))<=1e-2breakend% UPDATE THE HESSIANgradLEval = gradLagr(gradfEval,gradgEval,lNew,vars); % lnew not l!!!gradLEvalNew = gradLagr(gradfEvalNew,gradgEvalNew,lNew,vars);Q = gradLEvalNew-gradLEval;dx = xNew-x;HNew = UpdateH(H,dx,Q);% UPDATE ALL VALUES FOR NEXT ITERATIONH = HNew;fEval = fEvalNew;gEval = gEvalNew;gradfEval = gradfEvalNew;gradgEval = gradgEvalNew;P = PNew;x = xNew;
endfprintf('SQP: Optimum point:\n x1=%10.4f\n x2=%10.4f\n iterations =%10.0f \n', x(1), x(2), i)% FUNCTIONS NEEDEDfunction y = SolveKKT(gradfEval,gradgEval,gEval,Hessian)A = [Hessian -gradgEval';gradgEval 0];b = [-gradfEval -gEval]';y = A\b;
endfunction y = f(x)y = x(1)^4 - 2*x(2)*x(1)^2 + x(2)^2 + x(1)^2 - 2*x(1)+5;
endfunction y = gradf(x)y(1) = 2*x(1)-4*x(1)*x(2)+4*x(1)^3-2;y(2) = -2*x(1)^2 + 2*x(2);
endfunction y = gradLagr(gradfEval,gradgEval,l,n)y = gradfEval';sum = zeros(n,1);for i = 1:length(l)sum = sum -l(i)*gradgEval(i:n)';endy = y + sum;
endfunction y = gradg(x)y(1,1) = -2*x(1)-1/2;y(1,2) = 3/4;
endfunction y = g(x)y(1) = -(x(1)+0.25)^2+0.75*x(2);
endfunction [gViol,lViol] = Viols(gEval,l)gViol=[];lViol=[];for i = 1:length(gEval)if gEval(i)<0gViol(i)=gEval(i);lViol(i)=l(i);end end
endfunction y = Penalty(fEval,gViol,lViol)sum = 0;y = fEval;for i = 1:length(gViol)sum = sum + lViol(i)*abs(gViol(i));endy = y + sum;
endfunction y = UpdateH(H,dx,gamma)term1=(gamma*gamma') / (gamma'*dx);term2 = ((H*dx)*(dx'*H)) / (dx'*(H*dx));y = H + term1-term2;
end
最后输出结果为:
---------------------------------------------------------------
An implementation of Sequential Quadratic Programming method
in a nonlinear constrained optimization problem
---------------------------------------------------------------
SQP: Optimum point:x1= 0.4999x2= 0.7498iterations = 9 相关文章:
非线性约束的优化问题_序列二次规划算法代码
1. 理论部分 2. 序列二次规划算法代码及解析 3.完整代码 1.理论部分 a.约束优化问题的极值条件 库恩塔克条件(Kuhn-Tucker conditions,KT条件)是确定某点为极值点的必要条件。如果所讨论的规划是凸规划,那么库恩-塔克条件也是充分条件。 ÿ…...
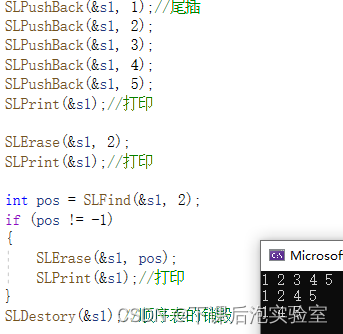
【数据结构之顺序表】
数据结构学习笔记---002 数据结构之顺序表1、介绍线性表1.1、什么是线性表? 2、什么是顺序表?2.1、概念及结构2.2、顺序表的分类 3、顺序表接口的实现3.1、顺序表动态存储结构的Seqlist.h3.1.1、定义顺序表的动态存储结构3.1.2、声明顺序表各个接口的函数 3.2、顺序表动态存储…...

junit-mock-dubbo
dubbo单元测试分两种情况 Autowired注解是启动上下文环境,使用上下文对象进行测试,适合调试代码 InjectMocks注解是启动上下文环境,使用mock对象替换上下文对象,适合单元测试 BaseTest *** Created by Luohh on 2023/2/10*/ S…...

json解析之fastjson和jackson使用对比
前言 最近项目中需要做埋点分析,首先就需要对埋点日志进行解析处理,刚好这时候体验对比了下fastjson和jackson两者使用的区别,以下分别是针对同一个json串处理,最终的效果都是将json数据解析出来,并统一展示。 一、fa…...

设计模式之-模板方法模式,通俗易懂快速理解,以及模板方法模式的使用场景
系列文章目录 设计模式之-6大设计原则简单易懂的理解以及它们的适用场景和代码示列 设计模式之-单列设计模式,5种单例设计模式使用场景以及它们的优缺点 设计模式之-3种常见的工厂模式简单工厂模式、工厂方法模式和抽象工厂模式,每一种模式的概念、使用…...
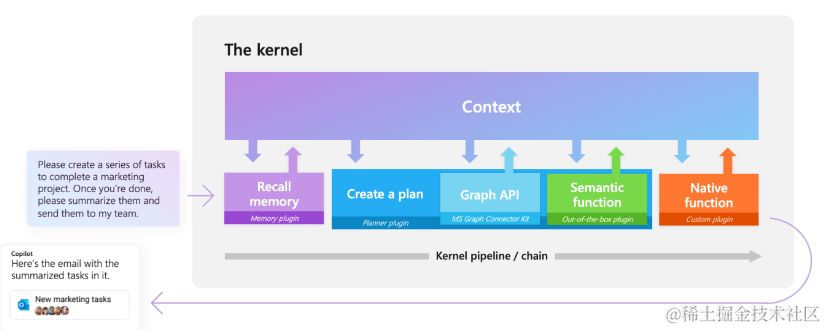
微软官方出品:GPT大模型编排工具,支持C#、Python等多个语言版本
随着ChatGPT的火热,基于大模型开发应用已经成为新的风口。虽然目前的大型模型已经具备相当高的智能水平,但它们仍然无法完全实现业务流程的自动化,从而达到用户的目标。 微软官方开源的Semantic Kernel的AI编排工具,就可以很好的…...

docker安装的php 在cli中使用
1: 修改 ~/.bashrc 中新增 php7 () {ttytty -s && tty--ttydocker run \$tty \--interactive \--rm \--volume /website:/website:rw \--workdir /website/project \--networkdnmp_dnmp \dnmp_php php "$" }–networkdnmp_dnmp 重要, 不然连不上数据库, 可通…...

tcp vegas 为什么好
我吹捧 bbr 时曾论证过它在和 buffer 拧巴的时候表现如何优秀,但这一次说 vegas 时,我说的是从拥塞控制这个问题本身看来,vegas 为什么好,并且正确。 接着昨天 tcp vegas 鉴赏 继续扯。 假设一群共享带宽的流量中有流量退出或有…...

【设计模式】命令模式
其他系列文章导航 Java基础合集数据结构与算法合集 设计模式合集 多线程合集 分布式合集 ES合集 文章目录 其他系列文章导航 文章目录 前言 一、什么是命令模式? 二、命令模式的优点和应用场景 三、命令模式的要素和实现 3.1 命令 3.2 具体命令 3.3 接受者 …...
Unity头发飘动效果
Unity头发飘动 介绍动作做头发飘动头发骨骼绑定模拟物理组件 UnityChan插件下载UnityChan具体用法确定人物是否绑定好骨骼节点(要做的部位比如头发等)给人物添加SpringManager骨骼管理器给骨骼节点添加SpringBone这里给每个头发骨骼都添加上SpringBone。…...

【MIKE】MIKE河网编辑器操作说明
目录 MIKE河网编辑器说明河网定义河网编辑工具栏河网文件(.nwk11)输入步骤1. 从传统的地图引入底图1.1 底图准备1.2 引入河网底图1.3 输入各河段信息2. 从ARCView .shp文件引入底图MIKE河网编辑器说明 河网编辑器主要功能有两个: ①河网的编辑和参数输人,包括数字化河网及…...

RIPV1配置实验
查看路由器路由表: 删除手工配置的静态路由项: Route1->Config->static Remove删除路由项 删除Route3的路由项,方法同上删除Route2的路由项,方法同上 完成路由器RIP配置: Route1->Config->RIP->Ne…...
快速实现农业机械设备远程监控
农业机械设备远程监控解决方案 一、项目背景 近年来,农业生产事故时有发生,农业安全问题已经成为农业生产中的关键问题,农业监控系统在农业安全生产中发挥着重要作用。农业机械设备以计划维修或定期保养为主,在日常应用的过程中因…...

解决用Fiddler抓包,网页显示你的连接不是专用/私密连接
关键:重置fiddler的证书 在Fiddler重置证书 1、Actions --> Reset All Certificates --> 弹窗一路yes 2、关掉Fiddler,重新打开 3、手机删掉证书,重新下载安装。 (如果还不行,重新试一遍,先把浏览器…...
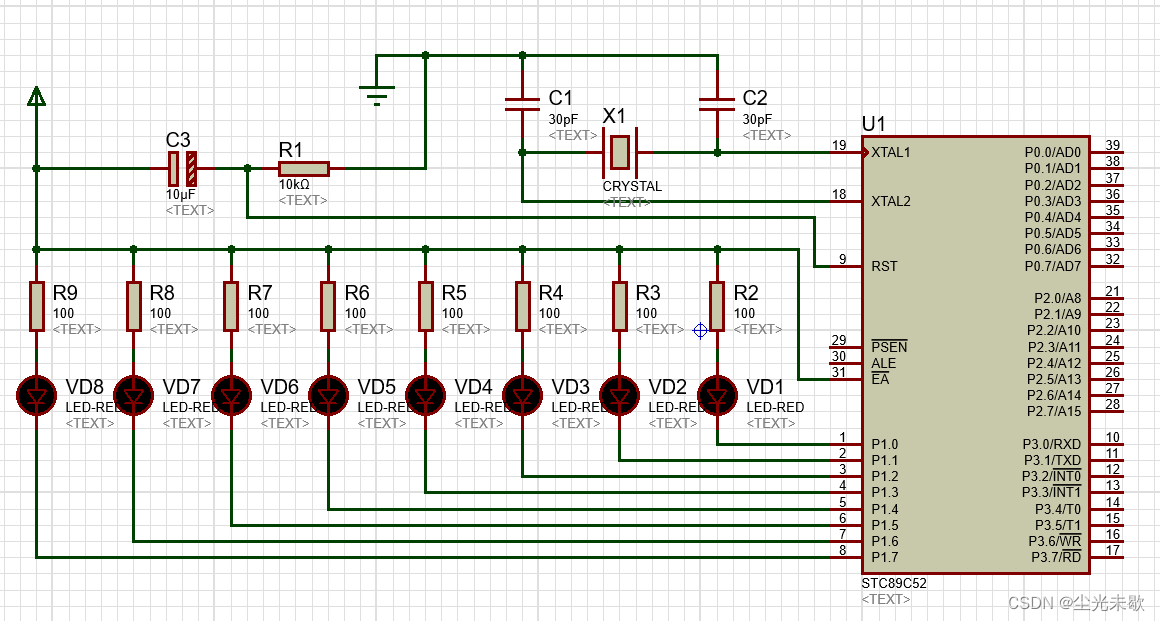
单片机原理及应用:流水灯的点亮
流水灯是一种简单的单片机控制电路,由许多LED组成,电路工作时LED会按顺序点亮,类似于流水的效果。 下面是运行在keil上的代码,分别使用了数组,移位符和库函数来表示。 //数组法 #include <reg52.h> //头文…...
)
蓝桥杯宝藏排序算法(冒泡、选择、插入)
冒泡排序: def bubble_sort(li): # 函数方式for i in range(len(li)-1):exchangeFalsefor j in range(len(li)-i-1):if li[j]>li[j1]:li[j],li[j1]li[j1],li[j]exchangeTrueif not exchange:return 选择排序: 从左往右找到最小的元素,放在起始位置…...
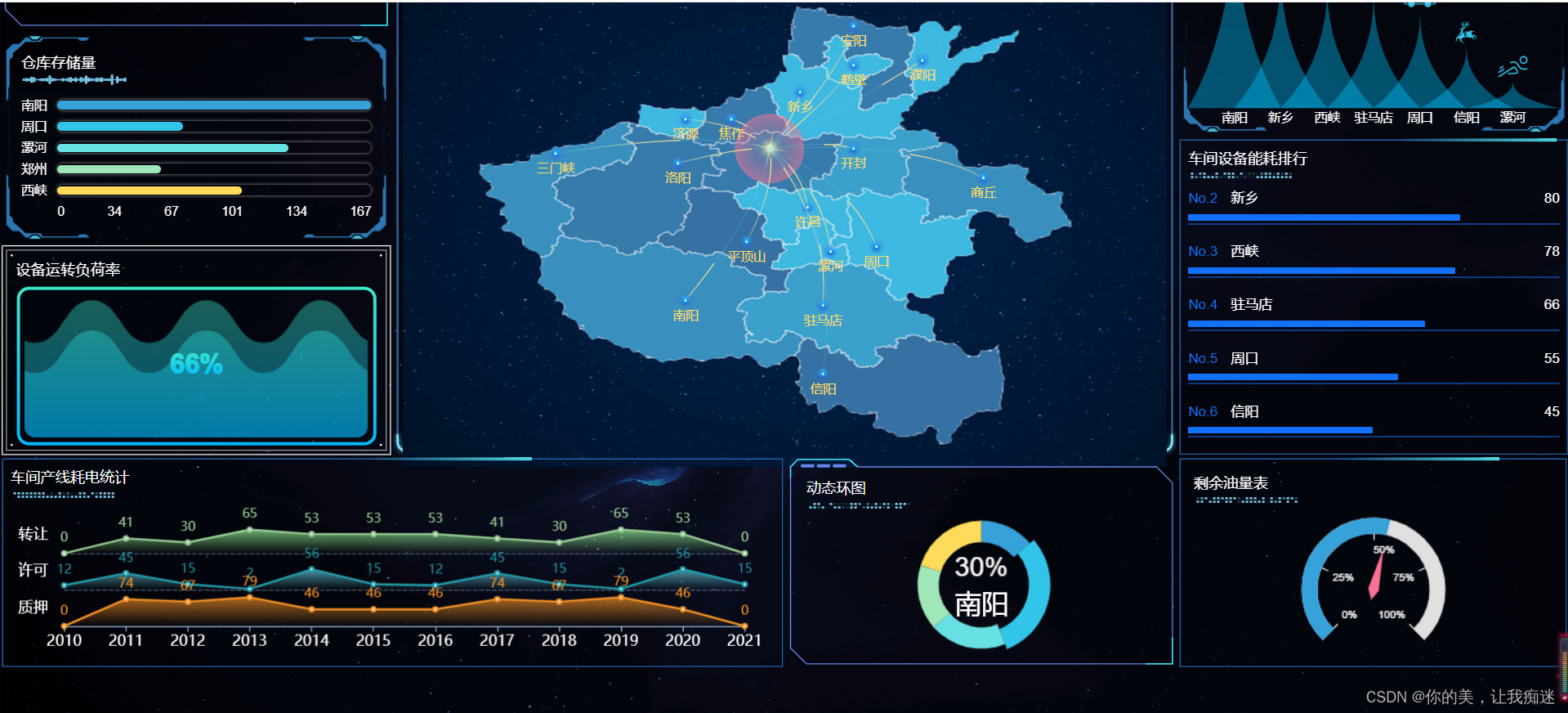
使用@jiaminghi/data-view实现一个数据大屏
<template><div class"content bg"><!-- 全局容器 --><!-- <dv-full-screen-container> --><!-- 第二行 --><div class"module-box" style"align-items: start; margin-top: 10px"><!-- 左 -->…...
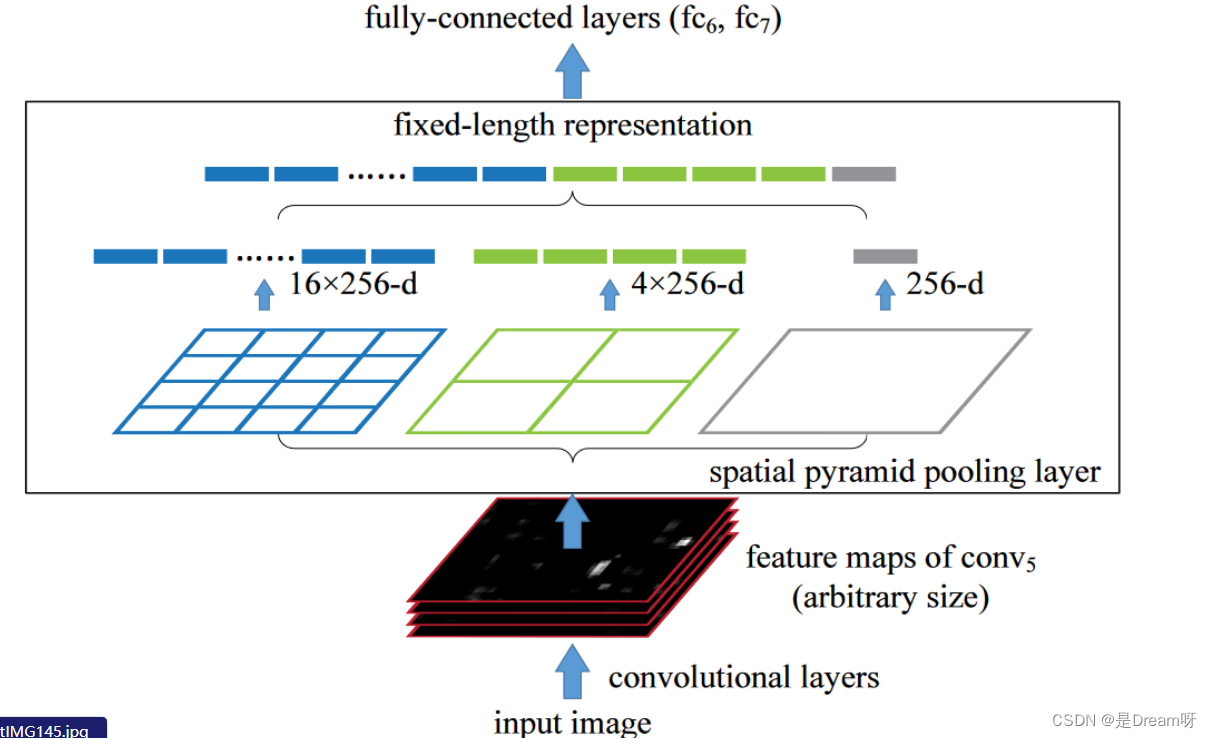
神经网络:池化层知识点
1.CNN中池化的作用 池化层的作用是对感受野内的特征进行选择,提取区域内最具代表性的特征,能够有效地减少输出特征数量,进而减少模型参数量。按操作类型通常分为最大池化(Max Pooling)、平均池化(Average Pooling)和求和池化(Sum Pooling)&a…...

微服务常见的配置中心简介
微服务架构中,常见的配置中心包括以下几种: Spring Cloud Config: Spring Cloud Config是官方推荐的配置中心解决方案,它支持将配置文件存储在Git、SVN等版本控制系统中。通过提供RESTful API,各个微服务可以远程获取和…...
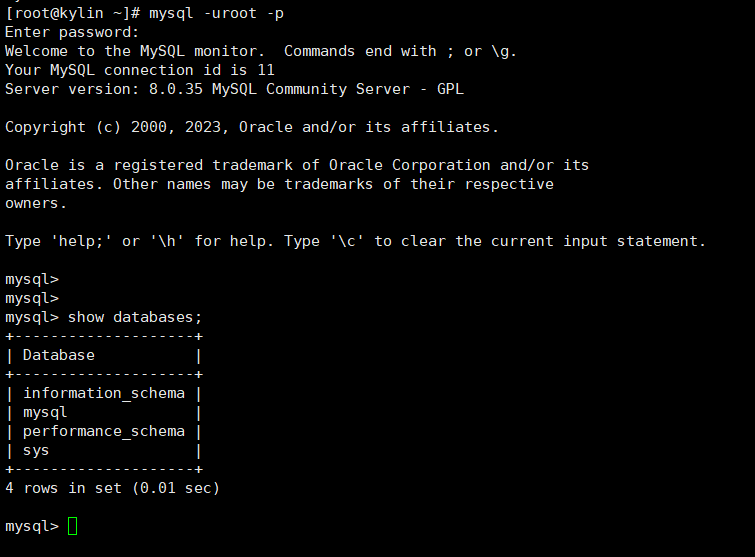
银河麒麟v10 rpm安装包 安装mysql 8.35
银河麒麟v10 rpm安装包 安装mysql 8.35 1、卸载mariadb2、下载Mysql安装包3、安装Mysql 8.353.1、安装Mysql 8.353.3、安装后配置 1、卸载mariadb 由于银河麒麟v10系统默认安装了mariadb 会与Mysql相冲突,因此首先需要卸载系统自带的mariadb 查看系统上默认安装的M…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...

电脑桌面太单调,用Python写一个桌面小宠物应用。
下面是一个使用Python创建的简单桌面小宠物应用。这个小宠物会在桌面上游荡,可以响应鼠标点击,并且有简单的动画效果。 import tkinter as tk import random import time from PIL import Image, ImageTk import os import sysclass DesktopPet:def __i…...

FTXUI::Dom 模块
DOM 模块定义了分层的 FTXUI::Element 树,可用于构建复杂的终端界面,支持响应终端尺寸变化。 namespace ftxui {...// 定义文档 定义布局盒子 Element document vbox({// 设置文本 设置加粗 设置文本颜色text("The window") | bold | color(…...
