机器学习 | 概率图模型
见微知著,睹始知终。
见到细微的苗头就能预知事物的发展方向,能透过微小的现象看到事物的本质,推断结论或者结果。
概率模型为机器学习打开了一扇新的大门,将学习的任务转变为计算变量的概率分布。
实际情况中,各个变量间存在显式或隐式的相互依赖,如朴素贝叶斯方法直接基于训练数据去求解变量的联合概率分布在时间复杂度还是空间复杂度均是不可行、不划算的。
直接基于训练数据求解变量联合概率分布困难。
Probabilistic Graphical Model,简称PGM,就是用图来表示变量概率间的依赖关系。
概率图模型可以简单的理解为 概率 + 图(结构)
它不仅可以刻画各个变量间的概率关系,还可以进行高效的推理。
结点表示随机变量,边表示变量间概率关系(一般是条件概率分布)
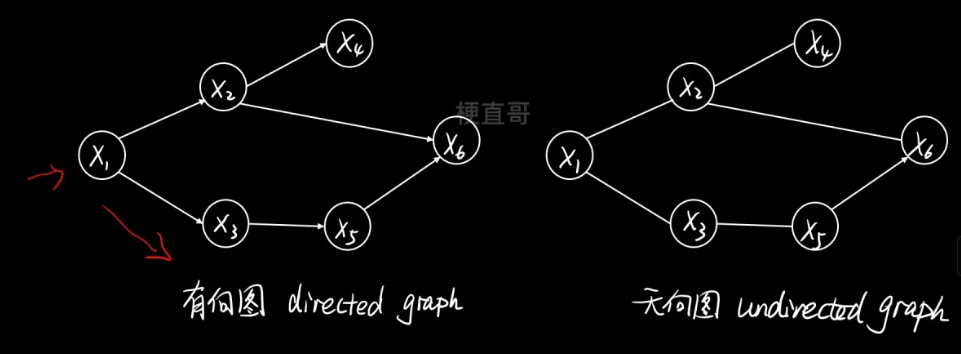
根据边是否有指向,分为有向图和无向图。
有向图可以显示的刻画变量间的因果(生成)关系。
无向图表示的只是一种关联关系或者说是相关关系。
1、核心思想及原理
概率图模型主要步骤
1、表示 Reprcntation ,将实际问题建模成某种图结构
2、推断 lnference,计算感兴趣的图节点的后验概率分布
3、学习 Learning,估计模型参数
通过第一步计算可以得到全体节点随机变量的联合概率分布,
我们的目的
是分析部分目标节点变量或者说根据一些观测到的数据求另外一些的变量,
用数学的语言来说就是 计算节点变量的条件概率分布和边际概率分布。
整体上求解他们的过程就是推断。
边际概率分布其实就是把其中一些不需要的变量通过求和或积分消去。
学习的过程就是参数估计的过程,通常使用最优化方法MLE或MAP求解。
但如果把参数也当成要去推测的变量,也算作一些节点,男参数估计就可以认为是推断的一部分,
所以一些书籍中也把推断和学习的过程统一为推断。
1.1、表示 —— 有向图 (也叫贝叶斯网络)
在结构上是一个网络,在概率分布上符合贝叶斯公式。可以表示任何的概率分布。
节点对应连续或离散随机变量。
有向边连接父子节点。从 xi指向xj,xi 就是父节点,xj 就是子节点。
有向边表示条件概率分布。
比如下图中,从x2指向x4的边就可以表示为 p (x4 | x2),先有爹才能有儿子。
图中不存在任何回路,又称为有向无环图模型。Directed Acyclic Graph,DAG。

一个概率图模型中的联合概率分布可以由概率中的乘法公式展开:
理论上只有父母有用。

比如:
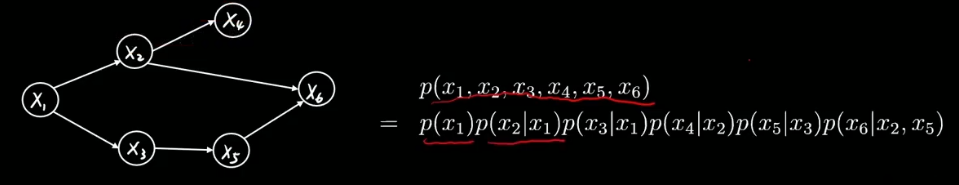
之前学过的各种模型,比如线性模型、神经网络都可以看成有向图模型,
他就像贝叶斯方法一样,在某种程度上把前面的所有模型在方法论层面高度统一到了一个框架下。
1.2、表示 —— 无向图(又叫马尔可夫网络 / 马尔可夫随机场)
节点对应连续或离散随机变量。
边表示依赖关系。
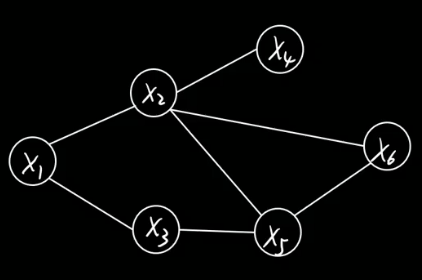
任意两节点间都有边连接,则该节点子集为团clique,比如下图中的x2 x5 x6。
联合概率分布能基于团分解.
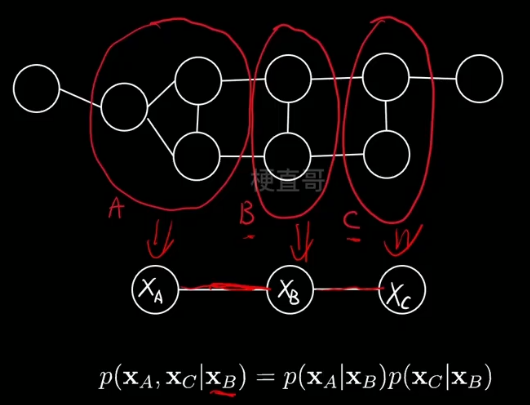
下例中,也就是说在给定xb的情况下,xa和xc就条件独立了。可以大大简化计算。
用数学语言来表示 所有节点的联合概率分布:
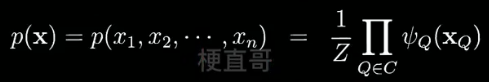
Q 表示某一个团,C是所有团的总称,
后面是团Q对应的势函数(一个概率分布,团伙的势力/影响力)
Z 归一化因子,确保整体求完还是一个概率,实际很难算,多数情况下只需要最优化求模型参数就可以,Z就类似于一个常数,所以不太需要
之所以这么分解的原因是要更好地利用条件独立,也就是马尔可夫性质。
有向图转无向图(也叫道德化)
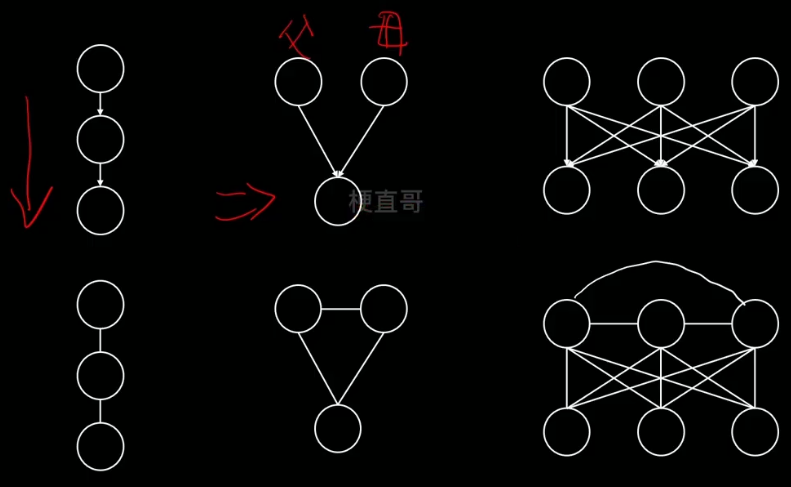
无向图转有向图
也分为两个步骤:
1、含有环状的结构三角化
2、弦图加箭头,箭头方向可以对节点的随机变量排序,较早的指向叫晚的
下图中间一张也叫弦图。
1.3、推断
精确推断法,比较理想,实际中很难实现。
重点掌握近似推断。
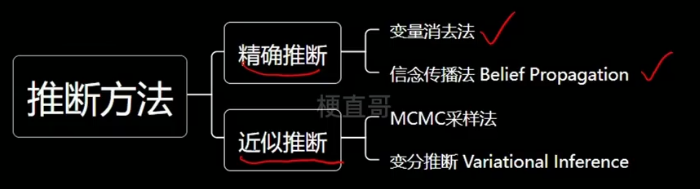
MCMC主要思想:
在很多时候我们关心的并不是概率分布本身而是他们的期望,根据这些期望做出决策。
去估计概率分布本身比较困难,就直接计算或逼近期望值。
变分推断主要思想:
通过使用已知的简单分布逼近需要推断的复杂分布。
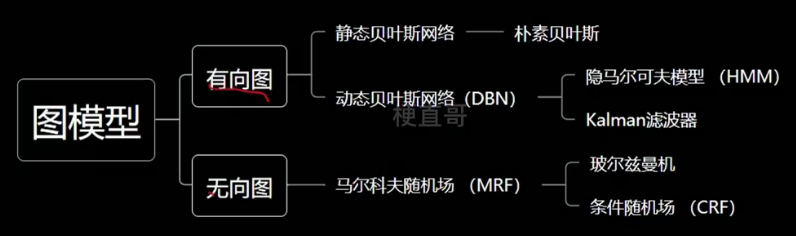
1.4、概率图模型家族
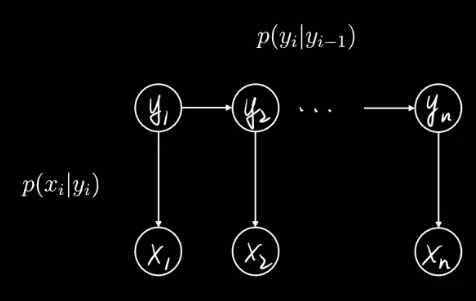
1.5、隐马尔科夫模型 Hidden Markov Model
假设有一系列的状态变量 yi,生成了一堆观测xi,
n可以是不同时间或先后顺序,’比如语音识别中就是时间先后,nlp分析中就是词的先后顺序,
我们听到的声音或者看到的文字就是观测。背后其实是有真实状态的。
数学上就是条件概率分布(也叫likelihood,贝叶斯公式中的似然函数),
因为状态未知,所以认为是隐藏的,又因为有先后顺序,就用一条有方向的链表示,
节点与节点之间符合马尔可夫性质,节点之间的关系就可以简化,就是隐马尔可夫链。
2、近似推断 EM算法参数估计
期望最大化算法,Expectation Maximization
概率图模型都可以简化为有两个节点的有向图:
z 是隐变量,x 是观测变量,箭头表示生成关系。
这两个节点本身也可以是向量,可以是一个集合,包含其他很多变量(节点)。
z 虽然未知,但是可以假定它含有一系列参数 θ,
观测 x 也满足一个带有参数 θ 的分布。
给定观测数据 x ,假定有 n 个样本,现在想要估计参数 θ 就可以:
最大化 似然函数 p( x | θ )。
假定 n 个样本是条件独立的,因为我们不太喜欢连乘,所以加上 log 运算,就变成了求和。
继续展开,引入隐变量 z ,就可以得到 每个样本每种可能的类别 z ,求联合概率分布之和。
z 如果是个已知的数,很容易用极大似然法求出 θ,
但现在 z 是隐变量,就用要 EM算法 近似推断。
注:那可以使用梯度下降法吗?
可以,但是当z过多时,求梯度时运算就会指数级的上升,EM效率更高。
z 是一个因变量,那该怎么求 x 和 z 的联合概率分布函数呢?
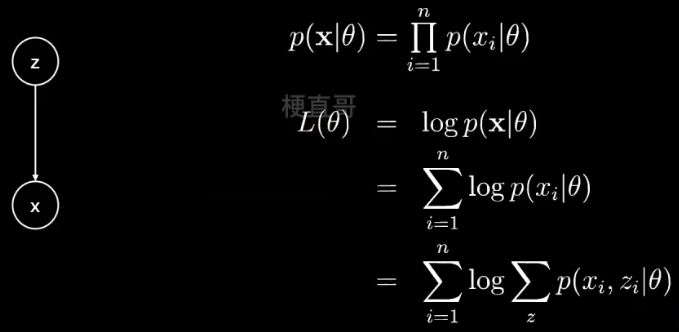
EM算法思想
目的:使得似然函数最大化
先猜一个 z 的分布,就是蓝色的分布,然后用它来逼近。
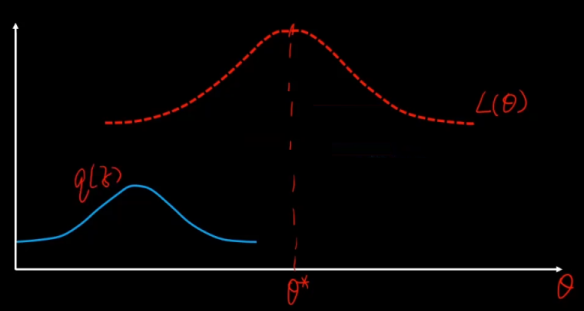
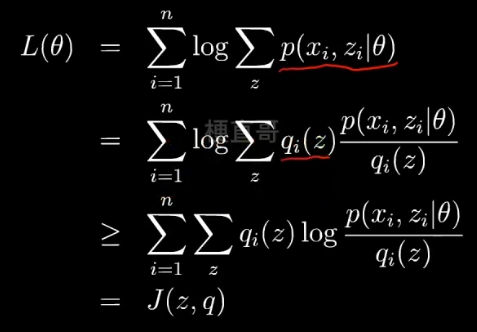
利用Jensen不等式:期望的函数 ≥ 函数的期望,
函数就是log函数,后面的一坨是期望,把q看成一个分布 分式看成z的函数。
现在就可以通过不断改变 z,q来搜索L(θ),从而找到他的最大值。
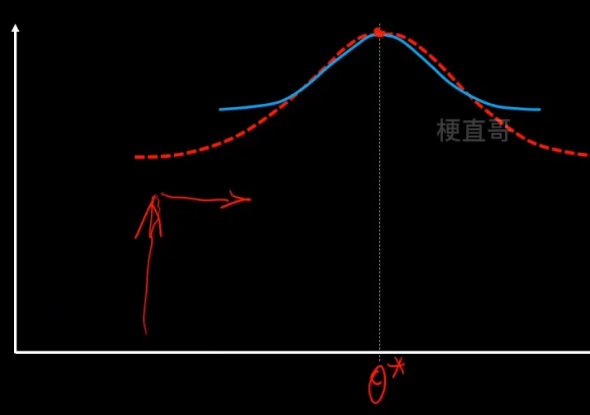
EM算法步骤
1、E步骤,先固定q分布不变(θ值不变),使用MLE来最大化z。
沿着固定的θ值,向上搜索,碰到红线之后就停止。
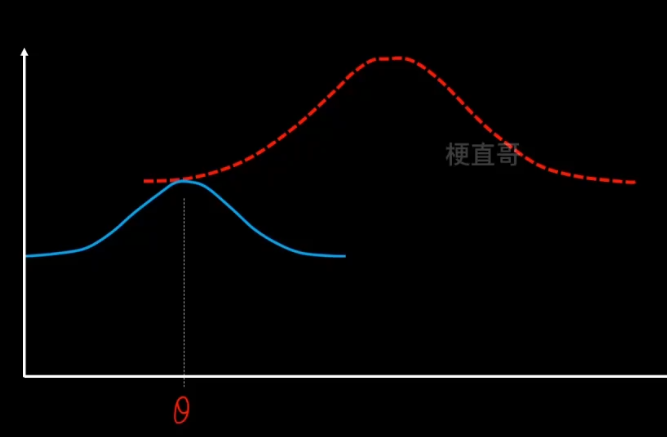
2、M步骤,固定z不变,让q最大化寻优。
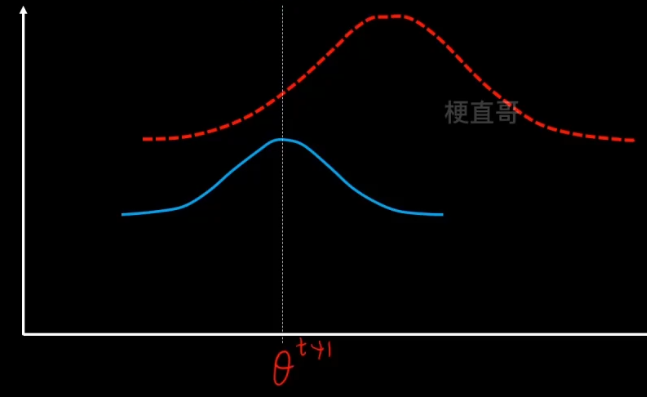
重复这个步骤,反复迭代,直到找到最优的θ*。
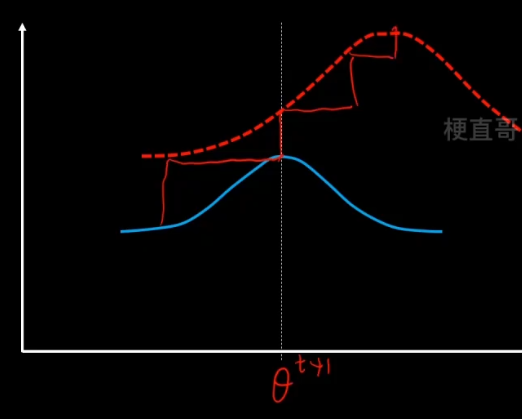
注意虽然EM的迭代一定会收敛,但是不一定收敛到最优的参数值,可能陷入局部最优,所以结果很受初始值的影响。
3、隐马尔可夫模型代码实现
对序列数据进行建模的有效办法。
隐马尔可夫模型对问题进行了简化,有两大基本假设:
1、任意时刻的观测只依赖于该时刻的马尔科夫链的状态,与其他的观测以及状态没有关系。
2、t 时刻的状态只与 t-1 时刻的状态有关,与其他时刻的状态和观测都无关。

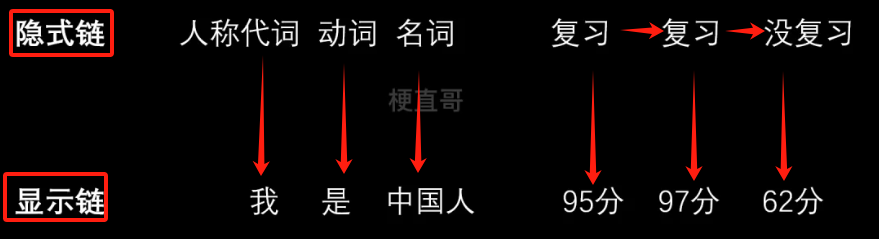
马尔可夫链 / 隐马尔可夫模型链
隐式链通常是一个状态的链。
简单的隐马模型
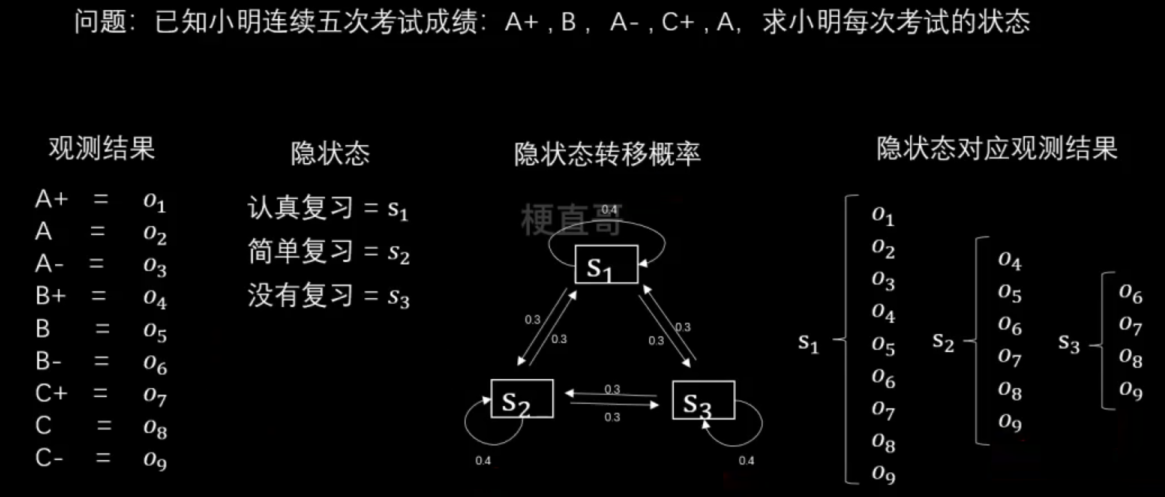
Example:
假设观测有9个等级,分别对应
状态有三种,假定保持状态不变的概率是0.4,三种状态之间互相转换的概率是0.3。
建模 —— 隐马模型三要素
发射概率矩阵,描述了在每种隐藏状态下发生观测值的概率。(就是可能性 / 似然函数)

现在我们就可以根据考试成绩序列 o 来推断出状态序列 s 的最大可能性了。
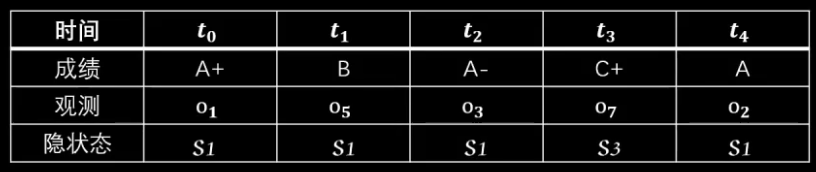
现在假设五次考试成绩如下:
1、首先根据发射概率矩阵列出每个时刻每种状态的概率。
2、用连线绘制出状态转移的情况。
3、因为 t0 时刻不涉及状态转移,所以要乘初始概率。
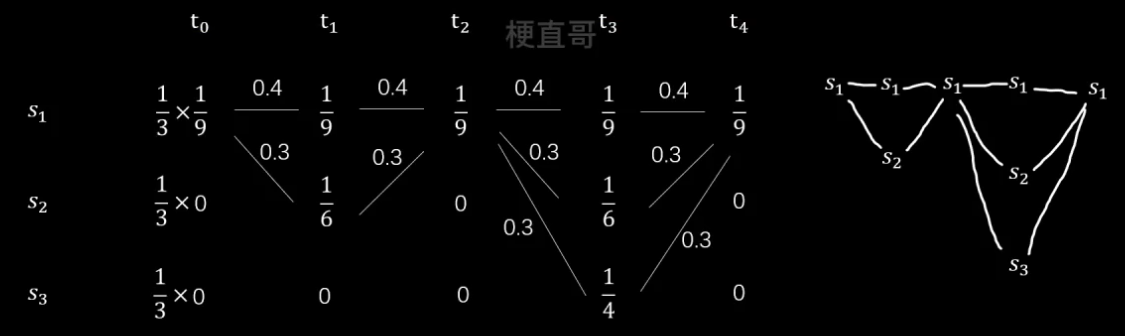
从前往后分析,
先来看 t1 时刻,有两个状态,s1对应的概率为 0.4 x 1/9,s2对应的概率为0.3 x 1/6
再看 t2 时刻,只有一个状态 s1,但第一条路线概率为 0.4x1/9+0.4x1/9 大于第二条路线 0.3x1/6+0.3x1/9,所以选择第一条路线。
同理,得到最终结果:
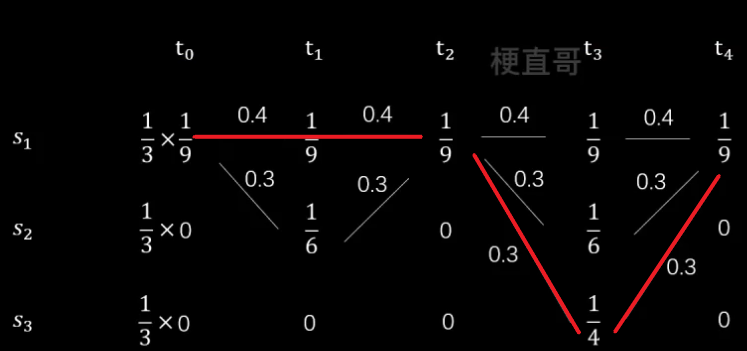
上述计算隐藏状态序列的方法就是维特比算法,是隐马模型最常用的解码方法。
代码实现:
hmmlearn —— CategoricalHMM
能力:
预测隐藏状态序列
预测观测序列概率
生成条件约束数据
数据准备
import numpy as np
state = np.array(['认真复习', '简单复习', '没有复习'])
grade = np.array(['A+', 'A', 'A-', 'B+', 'B', 'B-', 'C+', 'C', 'C-'])
n_state = len(state)
m_grade = len(grade)
pi = np.ones(n_state)/n_state
t = np.array([[0.4, 0.3, 0.3],[0.3, 0.4, 0.3],[0.3, 0.3, 0.4]
])
e = np.zeros([3,9])
e[0, :9]=1/9
e[1, 3:9]=1/6
e[2, 5:9]=1/4print("初始概率矩阵:\n",pi)
print("转移矩阵:\n",t)
print("发射矩阵:\n",e)初始概率矩阵:[0.33333333 0.33333333 0.33333333] 转移矩阵:[[0.4 0.3 0.3][0.3 0.4 0.3][0.3 0.3 0.4]] 发射矩阵:[[0.11111111 0.11111111 0.11111111 0.11111111 0.11111111 0.111111110.11111111 0.11111111 0.11111111][0. 0. 0. 0.16666667 0.16666667 0.166666670.16666667 0.16666667 0.16666667][0. 0. 0. 0. 0. 0.250.25 0.25 0.25 ]]
hmmlearn
pip install hmmlearnLooking in indexes: http://mirrors.tencentyun.com/pypi/simple Requirement already satisfied: hmmlearn in /home/ubuntu/.local/lib/python3.8/site-packages (0.2.8) Requirement already satisfied: scikit-learn>=0.16 in /home/ubuntu/.local/lib/python3.8/site-packages (from hmmlearn) (1.1.2) Requirement already satisfied: scipy>=0.19 in /usr/local/lib/python3.8/dist-packages (from hmmlearn) (1.8.0) Requirement already satisfied: numpy>=1.10 in /usr/local/lib/python3.8/dist-packages (from hmmlearn) (1.22.2) Requirement already satisfied: threadpoolctl>=2.0.0 in /home/ubuntu/.local/lib/python3.8/site-packages (from scikit-learn>=0.16->hmmlearn) (3.1.0) Requirement already satisfied: joblib>=1.0.0 in /home/ubuntu/.local/lib/python3.8/site-packages (from scikit-learn>=0.16->hmmlearn) (1.1.0) Note: you may need to restart the kernel to use updated packages.
from hmmlearn.hmm import CategoricalHMM
hmm = CategoricalHMM(n_state)此处我们选择适于离散值的categoricalHMM。
hmm.startprob_ = pi
hmm.transmat_ = t
hmm.emissionprob_ = e
hmm.n_feature = 9 #观测值个数因为HMM接受的参数是二维的,所以进行升维操作。
datas = np.array([0, 4, 2, 6, 1])
datas = np.expand_dims(datas, axis=1)
states = hmm.predict(datas)statesarray([0, 0, 0, 2, 0])
预测一下出现观测值的概率 :
prob = hmm.score(datas)
prob-14.003674820375014
这是取 In 之后的结果。
print(np.exp(prob))8.284786081615825e-07
因为每种观测值可能性是无限的,随着观测序列的加长,概率越来越低。
生成满足三要素约束的数据:
datas , states = hmm.sample(10000)验证是否满足约束:
t_2 = np.zeros([3,3])
for i in range(3):current = np.where(states == i)[0]next_index = current+1next_index = next_index[:-1]tmp = states[next_index]for j in range(3):t_2[i][j] = np.where(tmp==j)[0].shape[0]/np.shape(tmp)[0]
print(t_2)[[0.41121495 0.29333735 0.29544769][0.28884285 0.40988458 0.30127257][0.29627386 0.30930021 0.39442593]]
e_2 = np.zeros([3,9])
for i in range(3):current = np.where(states == i)[0]next_index = current+1next_index = next_index[:-1]tmp = datas[current]for j in range(9):e_2[i][j] = np.where(tmp==j)[0].shape[0]/np.shape(tmp)[0]
print(e_2)[[0.10518385 0.10066305 0.11030741 0.11603376 0.11000603 0.11060880.12115732 0.12085594 0.10518385][0. 0. 0. 0.1760355 0.15591716 0.162426040.17071006 0.16952663 0.16538462][0. 0. 0. 0. 0. 0.248637190.25741975 0.24500303 0.24894004]]
4、模型优缺点及发展方向
HMM算法优缺点
建立在一阶马尔可夫假设和观测独立假设之上。
很多场景下可以大大简化条件概率计算。
应用范围比较窄,主要用于时序数据建模。
概率图模型优缺点
不管问题复杂与否,处理思路都是:建模表示 + 推断学习,用图结构来表示,计算概率分布,然后进行推断和学习。对于复杂实际问题,特别是大型的人工智能系统来说是很有价值的,因为图模型中每个变量都有明确的解释,变量之间可以依赖专家或人工定义。所以可解释性强,相当于一个白盒字模型。
如何确定节点间拓扑关系,如何高效的进行推断和学习未知。
推断和学习复杂,高维数据处理困难。
概率图模型发展方向
动态化结构学习是概率图模型发展的一个方向。
非参数话建模是概率图模型可能的重要方向。
深度学习擅长感知类的任务,但不擅长推理和推断任务,深度学习和概率图结合也是未来发展的重要方向。
参考
机器学习必修课:经典算法与编程实战 梗直哥瞿炜_哔哩哔哩_bilibili
Chapter-14/14-4 隐马尔可夫模型代码实现.ipynb · 梗直哥/Machine-Learning - Gitee.com
相关文章:

机器学习 | 概率图模型
见微知著,睹始知终。 见到细微的苗头就能预知事物的发展方向,能透过微小的现象看到事物的本质,推断结论或者结果。 概率模型为机器学习打开了一扇新的大门,将学习的任务转变为计算变量的概率分布。 实际情况中,各个变量…...

25、新加坡南洋理工、新加坡国立大学提出FBCNet:完美融合FBCSP的CNN,EEG解码SOTA水准![抱歉老师,我太想进步了!]
前言: 阴阳差错,因工作需要,需要查阅有关如何将FBCSP融入CNN中的文献,查阅全网,发现只此一篇文章,心中大喜,心想作者哪家单位,读之,原来是自己大导(新加坡工…...

单调栈分类、封装和总结
作者推荐 map|动态规划|单调栈|LeetCode975:奇偶跳 通过枚举最小(最大)值不重复、不遗漏枚举所有子数组 C算法:美丽塔O(n)解法单调栈左右寻找第一个小于maxHeight[i]的left,right,[left,right]直接的高度都是maxHeight[i] 可以…...

【Amazon 实验①】使用 Amazon CloudFront加速Web内容分发
文章目录 实验架构图1. 准备实验环境2. 创建CloudFront分配、配置动、静态资源分发2.1 创建CloudFront分配,添加S3作为静态资源源站2.2 为CloudFront分配添加动态源站 在本实验——使用CloudFront进行全站加速中,将了解与学习Amazon CloudFront服务&…...

<math.h> 头文件:C语言数学库函数
文章目录 概述基本算术运算sqrt()fabs()pow() 三角函数sin()cos() 对数函数log()log10() 指数函数exp() 其他函数ceil()floor() 结语 概述 math.h 是C语言标准库中的头文件,提供了许多与数学运算相关的函数。在本文中,我们将深入讨论一些 math.h 中常用…...

1.CentOS7网络配置
CentOS7网络配置 查看网络配置信息 ip addr 或者 ifconfig 修改网卡配置信息 vim /etc/sysconfig/network-scripts/ifcfg-ens192 设备类型:TYPEEthernet地址分配模式:BOOTPROTOstatic网卡名称:NAMEens192是否启动:ONBOOTye…...

Prompt-to-Prompt:基于 cross-attention 控制的图像编辑技术
Hertz A, Mokady R, Tenenbaum J, et al. Prompt-to-prompt image editing with cross attention control[J]. arXiv preprint arXiv:2208.01626, 2022. Prompt-to-Prompt 是 Google 提出的一种全新的图像编辑方法,不同于任何传统方法需要用户指定编辑区域ÿ…...

搭载紫光展锐芯的移远通信RedCap模组顺利通过中国联通OPENLAB实验室认证
近日,移远通信联合紫光展锐在中国联通5G物联网OPENLAB开放实验室,完成了RedCap模组RG207U-CN端到端测试验收,并获颁认证证书。移远通信RG207U-CN成为业内率先通过联通OPENLAB认证的紫光展锐RedCap芯片平台的模组。 本次测试基于联通OPENLAB实…...

16-高并发-队列术
队列,在数据结构中是一种线性表,从一端插入数据,然后从另一端删除数据。 在我们的系统中,不是所有的处理都必须实时处理,不是所有的请求都必须实时反馈结果给用户,不是所有的请求都必须100%一次性处理成功…...
【设计模式-2.5】创建型——建造者模式
说明:本文介绍设计模式中,创建型设计模式中的最后一个,建造者模式; 入学报道 创建型模式,关注于对象的创建,建造者模式也不例外。假设现在有一个场景,高校开学,学生、教师、职工都…...

VideoPoet: Google的一种用于零样本视频生成的大型语言模型
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...

pytest常用命令行参数
文章目录 一、前置说明二、操作步骤1. 命令行中执行:pytest2. 命令行中执行:pytest - v3. 命令行中执行:pytest -s4. 命令行中执行:pytest -k test_addition5. 命令行中执行:pytest -k test_pytest_command_params.py6. 命令行中执行:pytest -v -s -k test_pytest_comman…...

05. Springboot admin集成Actuator(一)
目录 1、前言 2、Actuator监控端点 2.1、健康检查 2.2、信息端点 2.3、环境信息 2.4、度量指标 2.5、日志文件查看 2.6、追踪信息 2.7、Beans信息 2.8、Mappings信息 3、快速使用 2.1、添加依赖 2.2、添加配置文件 2.3、启动程序 4、自定义端点Endpoint 5、自定…...
AI生成SolidUI-新版本架构调试Debug
背景 SolidUI 0.5.0 版本重构全新版本架构。 dev-python 新架构临时分支,架构调整完后,所有代码合并到dev分支 https://github.com/CloudOrc/SolidUI 使用 设置参数 FLASK_DEBUG 设置 在开发过程中,Web框架的服务器通常会监视代码的变…...

ctfshow sql 195-200
195 堆叠注入 十六进制 if(preg_match(/ |\*|\x09|\x0a|\x0b|\x0c|\x0d|\xa0|\x00|\#|\x23|\|\"|select|union|or|and|\x26|\x7c|file|into/i, $username)){$ret[msg]用户名非法;die(json_encode($ret));}可以看到没被过滤,select 空格 被过滤了,可…...
)
微信小程序实现地图功能(腾讯地图)
微信小程序实现地图功能(腾讯地图) 主要功能 通过微信 API 获取用户当前位置信息 使用腾讯地图 API 将经纬度转换为地址信息 显示当前位置信息以及周围的 POI(兴趣点) 代码实现 index.wxml <!-- index.wxml --> <view class"container&…...
Vue如何请求接口——axios请求
1、安装axios 在cmd或powershell打开文件后,输入下面的命令 npm install axios 可在项目框架中的package.json中查看是否: 二、引用axios import axios from axios 在需要使用的页面中引用 三、get方式使用 get请求使用params传参,本文只列举常用参数…...
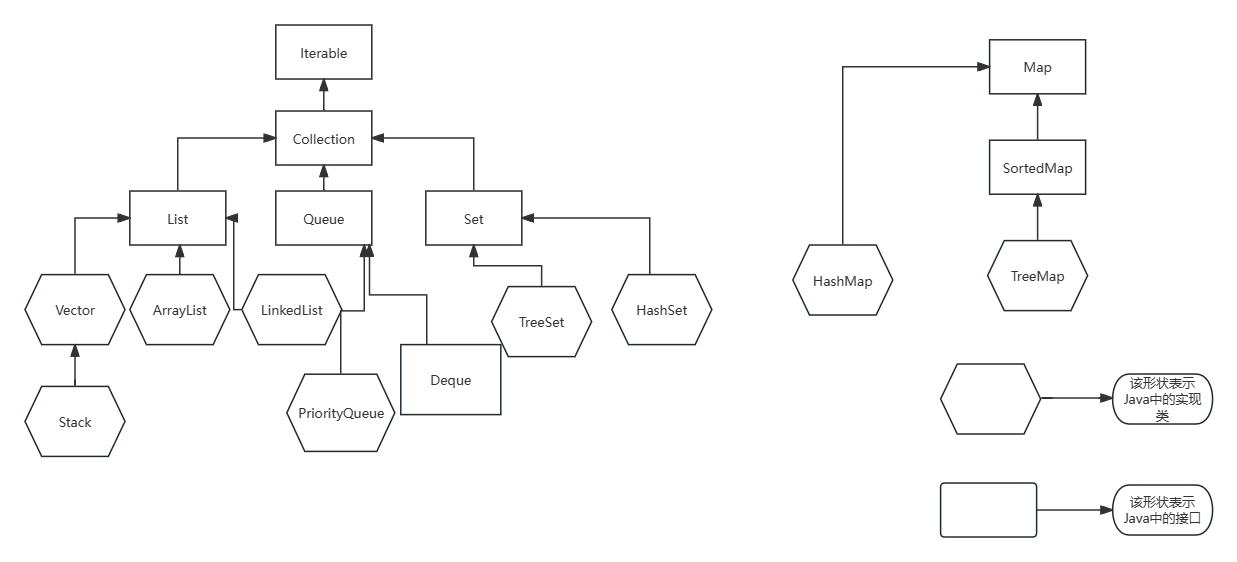
【数据结构一】初始Java集合框架(前置知识)
Java中的数据结构 Java语言在设计之初有一个非常重要的理念便是:write once,run anywhere!所以Java中的数据结构是已经被设计者封装好的了,我们只需要实例化出想使用的对象,便可以操作相应的数据结构了,本篇…...

直接将第三方数据插入到 Redis 中
Redis 是一个内存数据库,可以用于缓存和持久化数据。虽然常见的使用场景是将数据从关系型数据库(如MySQL)同步到 Redis 中进行缓存,但也可以直接将第三方数据插入到 Redis 中。 你可以通过编程语言的 Redis 客户端库(…...

【重点】【DP】322.零钱兑换
题目 法1:动态规划 // 时间复杂度:O(kN) class Solution {public int coinChange(int[] coins, int amount) {int[] dp new int[amount 1];Arrays.fill(dp, amount 1);dp[0] 0;for (int i 1; i < dp.length; i) {for (int coin : coins) {if (…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

