Pinely Round 3 (Div. 1 + Div. 2)(A~D)(有意思的题)
A - Distinct Buttons
题意:
思路:模拟从(0,0)到每个位置需要哪些操作,如果总共需要4种操作就输出NO。
// Problem: A. Distinct Buttons
// Contest: Codeforces - Pinely Round 3 (Div. 1 + Div. 2)
// URL: https://codeforces.com/contest/1909/problem/0
// Memory Limit: 256 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second
#define endl '\n'
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f3f3f;
const LL llinf = 5e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
vector<int>a(N , 0);
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
void solve()
{cin >> n;int flag[4] = {0 , 0 , 0 , 0};for(int i = 0 ; i < n ; i ++){int x , y;cin >> x >> y;if(x < 0){flag[0] = 1;}else if(x > 0){flag[1] = 1;}if(y < 0){flag[2] = 1;}else if(y > 0){flag[3] = 1;}} int cnt = 0;for(int i = 0 ; i < 4 ; i ++){cnt += flag[i];}if(cnt <= 3){cout <<"Yes\n";}else{cout <<"NO\n";}
}
int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;cin>>t;while(t--){solve();}return 0;
}B - Make Almost Equal With Mod

思路:比较有意思的题目,可以发现k取2的倍数即可。证明如下:将所有数变为二进制表示,那么某个数模2的结果即二进制最后一位,模4的结果即二进制倒数第二位...如此类推。
由于题目必然存在解,也就是说数组不可能全相等。既然不可能全相等,那一定存在整个数组某一位存在1和0。因此k取2的倍数必然能够满足题意。
// Problem: B. Make Almost Equal With Mod
// Contest: Codeforces - Pinely Round 3 (Div. 1 + Div. 2)
// URL: https://codeforces.com/contest/1909/problem/B
// Memory Limit: 256 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second
#define endl '\n'
#define int long long
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f3f3f;
const LL llinf = 1e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
vector<int>a(N , 0);
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
void solve()
{cin >> n;int cnt1 = 0 , cnt0 = 0;for(int i = 0 ; i < n ; i++){cin >> a[i];}for(int j = 2 ; j <= llinf ; j *= 2){set<int>st;for(int i = 0 ;i < n ; i ++){st.insert(a[i] % j);}if(st.size() == 2){cout << j << endl;return;;}}}
signed main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;cin>>t;while(t--){solve();}return 0;
}
C - Heavy Intervals
题意:
思路:首先想到对l,r,c数组进行排序。可以发现,无论如何排序,所有区间长度之和是不会改变的。因此要让权值之和最小,需要让小的区间尽可能小。即对于任意而言,
为最靠近它的元素。而从小到大的处理
可以保证不会影响到后面的数。
// Problem: C. Heavy Intervals
// Contest: Codeforces - Pinely Round 3 (Div. 1 + Div. 2)
// URL: https://codeforces.com/contest/1909/problem/C
// Memory Limit: 256 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second
#define endl '\n'
#define int long long
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f3f3f;
const LL llinf = 5e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
vector<int>a(N , 0);
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
void solve()
{cin >> n;int l[n] , r[n] , c[n];for(int i = 0 ; i < n ; i ++)cin >> l[i];for(int i = 0 ; i < n ; i ++)cin >> r[i];for(int i = 0 ; i < n ; i ++)cin >> c[i];sort(c , c + n);sort(l , l + n);sort(r , r + n);int pre[n];stack<int>st;int ll = 0;int ans = 0;for(int i = 0 ; i < n ;i ++){while(ll < n && r[i] > l[ll]){st.push(l[ll]);ll++;}int x = st.top();st.pop();pre[i] = r[i] - x;} sort(pre , pre + n);for(int i = 0 ; i < n ; i ++){ans += pre[i] * c[n - i - 1];}cout << ans << endl;
}
signed main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;cin>>t;while(t--){solve();}return 0;
}
D - Split Plus K
题意:
思路:假设最终所有数为,对于
而言,需要操作
次以后能变成ans,需要满足
。
转换一下后得到
即成立的条件为:
为了方便解释,假设所有数都大于。想要操作数最小,即
需要最大。可以发现,最终的
的最大值为
。求出gcd之后再带回原式子求出操作数
即可。相反所有数都小于
也是一样的操作。需要注意存在数等于
时,需要所有数都等于
,否则输出-1。
// Problem: D. Split Plus K
// Contest: Codeforces - Pinely Round 3 (Div. 1 + Div. 2)
// URL: https://codeforces.com/contest/1909/problem/D
// Memory Limit: 256 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second
#define endl '\n'
#define int long long
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f3f3f;
const LL llinf = 5e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
vector<int>a(N , 0);
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
void solve()
{// x + tk = (t + 1) * ans
// x - ans = t(ans - k)
// ans - k < 0 ??
// (x - ans / ans - k ) = t // ans 越大越好cin >> n >> m;for(int i = 0 ; i < n ; i++)cin >> a[i];sort(a.begin() , a.begin() + n);for(int i = 0 ; i < n ; i ++){if(a[0] < m && a[i] >= m){cout << -1 << endl;return;}}for(int i = 0 ; i < n ; i ++){a[i] -= m;}int ans = 0;for(int i = 0 ; i < n ; i ++){ans = gcd(ans , abs(a[i]));}int out = 0;if(a[0] == 0 && a[n - 1] != 0 || a[0] != 0 && a[n - 1] == 0){cout << -1 << endl;return;}else if(ans == 0){cout << 0 << endl;return;}for(int i = 0 ; i < n ; i ++){if(a[i] >= 0){out += (a[i] - ans) / ans ;}else{out += (a[i] + ans) / -ans;}}cout << out << endl;
}
signed main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;cin>>t;while(t--){solve();}return 0;
}
相关文章:
Pinely Round 3 (Div. 1 + Div. 2)(A~D)(有意思的题)
A - Distinct Buttons 题意: 思路:模拟从(0,0)到每个位置需要哪些操作,如果总共需要4种操作就输出NO。 // Problem: A. Distinct Buttons // Contest: Codeforces - Pinely Round 3 (Div. 1 Div. 2) // URL: https…...

在Linux下探索MinIO存储服务如何远程上传文件
🌈个人主页:聆风吟 🔥系列专栏:网络奇遇记、Cpolar杂谈 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 📋前言一. 创建Buckets和Access Keys二. Linux 安装Cpolar三. 创建连接MinIO服务公网地…...

持续集成交付CICD:Linux 部署 Jira 9.12.1
目录 一、实验 1.环境 2.K8S master节点部署Jira 3.Jira 初始化设置 4.Jira 使用 一、实验 1.环境 (1)主机 表1 主机 主机架构版本IP备注master1K8S master节点1.20.6192.168.204.180 jenkins slave (从节点) jira9.12.1…...

Linux命令-查看内存、GC情况及jmap 用法
查看进程占用内存、CPU使用情况 1、查看进程 #jps 查看所有java进程 #top 查看cpu占用高进程 输入m :根据内存排序 topMem: 16333644k total, 9472968k used, 6860676k free, 165616k buffers Swap: 0k total, 0k used, 0k free, 6…...

nginx安装letsencrypt证书
1.安装推荐安装letsencrypt证书的客户端工具 官方推荐通过cerbot客户端安装letsencrypt 官方推荐使用snap客户端安装cerbot客户端 apt install snapd snap install --classic certbot 建立certbot软链接:ln -s /snap/bin/certbot /usr/bin/certbot 2.开始安装letse…...
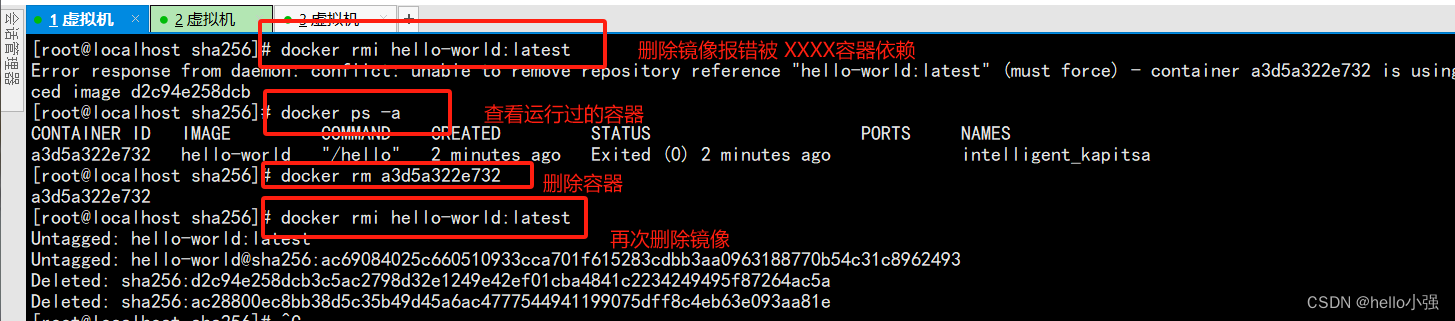
docker笔记1-安装与基础命令
docker的用途: 可以把应用程序代码及运行依赖环境打包成镜像,作为交付介质,在各种环境部署。可以将镜像(image)启动成容器(container),并提供多容器的生命周期进行管理(…...
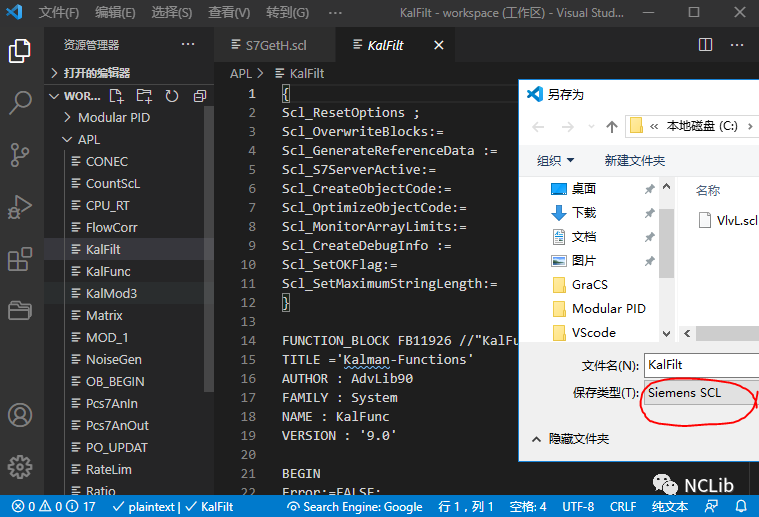
VSCode软件与SCL编程
原创 NingChao NCLib 博途工控人平时在哪里技术交流博途工控人社群 VSCode简称VSC,是Visual studio code的缩写,是由微软开发的跨平台的轻量级编辑器,支持几乎所有主流的开发语言的语法高亮、代码智能补全、插件扩展、代码对比等,…...
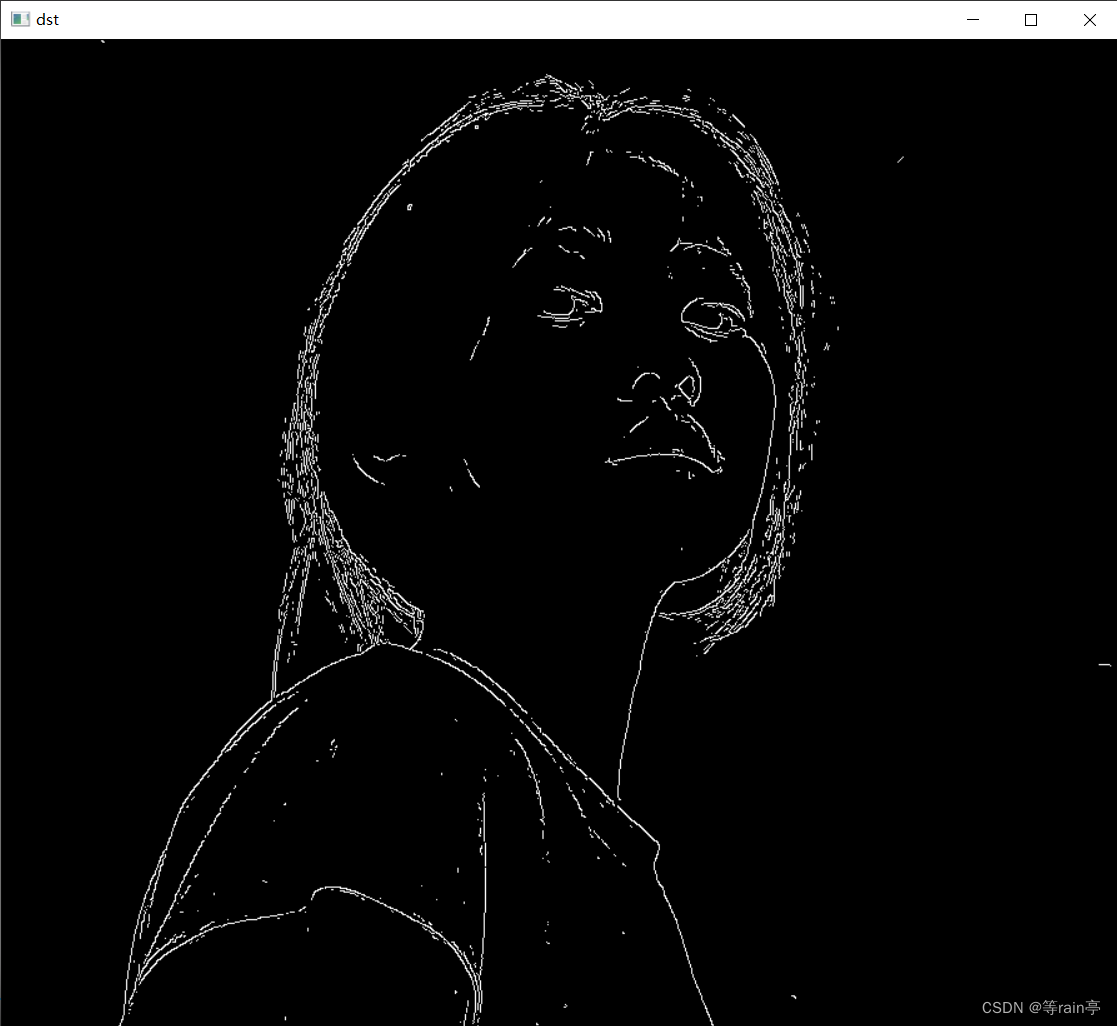
Opencv中的滤波器
一副图像通过滤波器得到另一张图像,其中滤波器又称为卷积核,滤波的过程称之为卷积。 这就是一个卷积的过程,通过一个卷积核得到另一张图片,明显发现新的到的图片边缘部分更加清晰了(锐化)。 上图就是一个卷…...

<JavaEE> 基于 TCP 的 Socket 通信模型
目录 一、认识相关API 1)ServerSocket 2)Socket 二、TCP字节流套接字通信模型概述 三、回显客户端-服务器 1)服务器代码 2)客户端代码 一、认识相关API 1)ServerSocket ServerSocket 常用构造方法ServerSocke…...
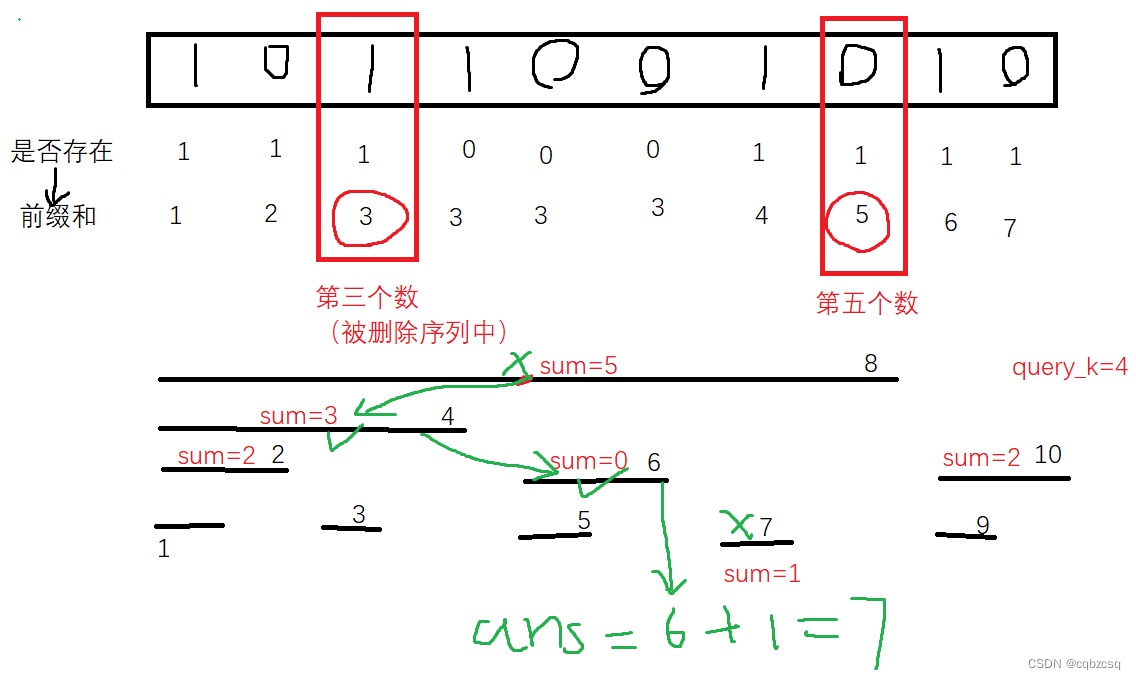
[THUPC 2024 初赛] 二进制 (树状数组单点删除+单点查询)(双堆模拟set)
题解 题目本身不难想 首先注意到所有查询的序列长度都是小于logn级别的 我们可以枚举序列长度len,然后用类似滑动窗口的方法,一次性预处理出每种字串的所有出现位置,也就是开N个set去维护所有的位置。预处理会进行O(logn)轮,每…...
机器学习算法(11)——集成技术(Boosting——梯度提升)
一、说明 在在这篇文章中,我们学习了另一种称为梯度增强的集成技术。这是我在机器学习算法集成技术文章系列中与bagging一起介绍的一种增强技术。我还讨论了随机森林和 AdaBoost 算法。但在这里我们讨论的是梯度提升,在我们深入研究梯度提升之前…...

使用GBASE南大通用负载均衡连接池
若要使用负载均衡连接池功能,需要在连接串中配置相关的关键字。有关更详细的关键字信息在 GBASE南大通用 连接参数表‛中介绍。假设存在如下场景: 现有集群中存在 4 个节点: 192.168.9.173, 192.168.9.174, 192.168.9.175, 192.168.9.17…...
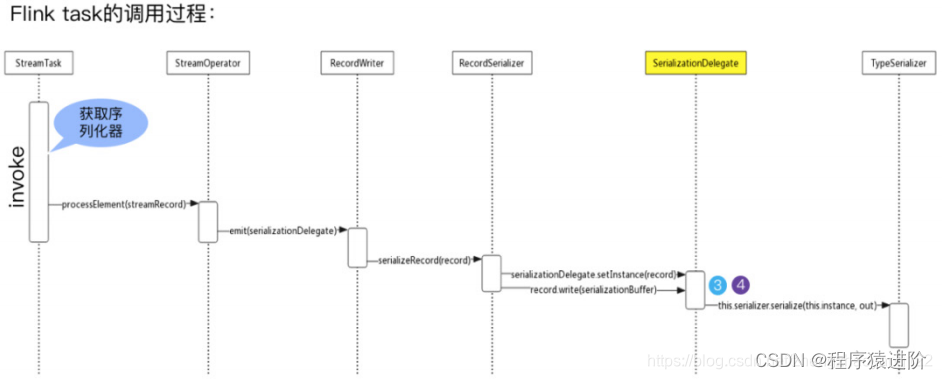
Flink 数据序列化
为 Flink 量身定制的序列化框架 大家都知道现在大数据生态非常火,大多数技术组件都是运行在JVM上的,Flink也是运行在JVM上,基于JVM的数据分析引擎都需要将大量的数据存储在内存中,这就不得不面临JVM的一些问题,比如Ja…...
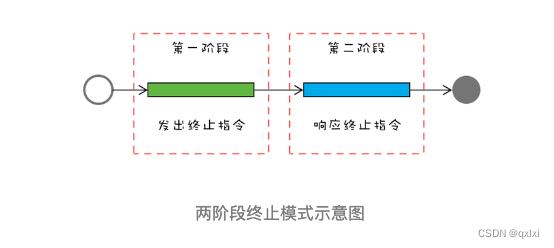
【并发设计模式】聊聊两阶段终止模式如何优雅终止线程
在软件设计中,抽象出了23种设计模式,用以解决对象的创建、组合、使用三种场景。在并发编程中,针对线程的操作,也抽象出对应的并发设计模式。 两阶段终止模式- 优雅停止线程避免共享的设计模式- 只读、Copy-on-write、Thread-Spec…...
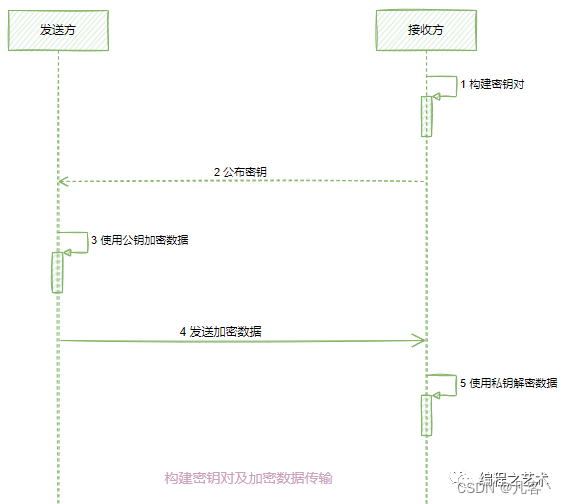
Java实现非对称加密【详解】
Java实现非对称加密 1. 简介2. 非对称加密算法--DH(密钥交换)3. 非对称加密算法--RSA非对称加密算法--EIGamal5. 总结6 案例6.1 案例16.2 案例2 1. 简介 公开密钥密码学(英语:Public-key cryptography)也称非对称式密…...

simulinkveristandlabview联合仿真——模型导入搭建人机界面
目录 1.软件版本 2.搭建simulink仿真模型 编译错误 3.导入veristand并建立工程 4.veristand导入labview labview显示veristand工程数据 labview设置veristand工程数据 运行labview工程 1.软件版本 matlab2020a,veristand2020 R4,labview2020 SP…...
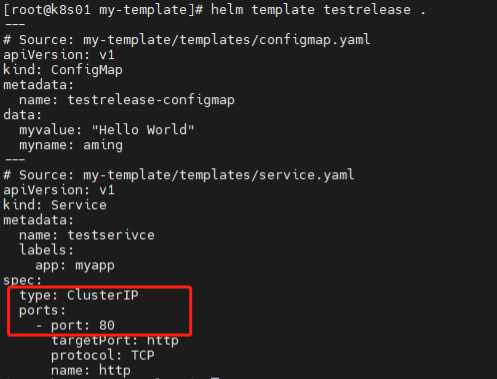
k8s中Helm工具实践
k8s中Helm工具实践 1)安装redis-cluster 先搭建一个NFS的SC(只需要SC,不需要pvc),具体步骤此文档不再提供,请参考前面相关章节。 下载redis-cluster的chart包 helm pull bitnami/redis-cluster --untar…...
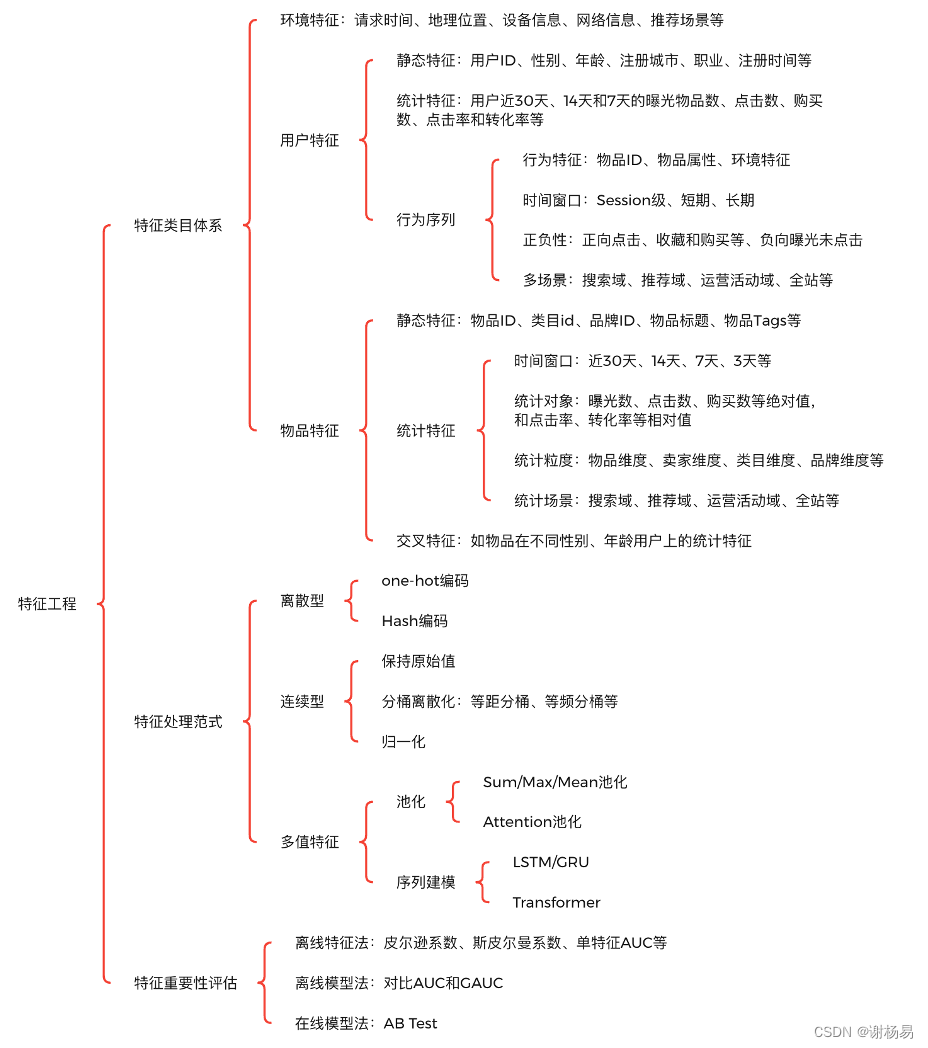
推荐算法架构7:特征工程(吊打面试官,史上最全!)
系列文章,请多关注 推荐算法架构1:召回 推荐算法架构2:粗排 推荐算法架构3:精排 推荐算法架构4:重排 推荐算法架构5:全链路专项优化 推荐算法架构6:数据样本 推荐算法架构7:特…...
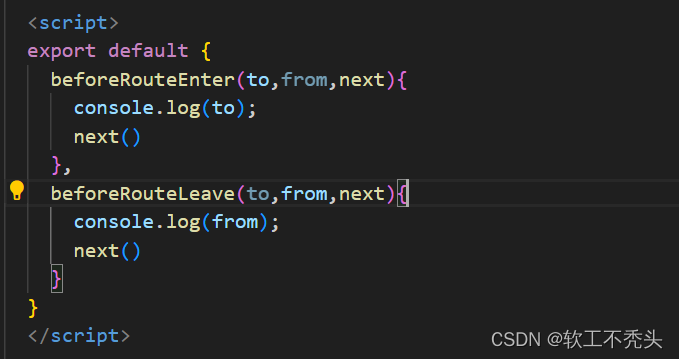
Web前端 ---- 【Vue】vue路由守卫(全局前置路由守卫、全局后置路由守卫、局部路由path守卫、局部路由component守卫)
目录 前言 全局前置路由守卫 全局后置路由守卫 局部路由守卫之path守卫 局部路由守卫之component守卫 前言 本文介绍Vue2最后的知识点,关于vue的路由守卫。也就是鉴权,不是所有的组件任何人都可以访问到的,需要权限,而根据权限…...

uniapp点击tabbar之前做判断
在UniApp中,可以通过监听 tabBar 的 click 事件来在点击 tabBar 前做判断。具体步骤如下: 在 pages.json 文件中配置 tabBar,例如: {"pages":[{"path":"pages/home/home","name":"h…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...
