力扣(leetcode)第26题删除有序数组中的重复项(Python)
26.删除有序数组的重复项
题目链接:26.删除有序数组的重复项
给你一个非严格递增排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。
考虑 nums 的唯一元素的数量为 k ,你需要做以下事情确保你的题解可以被通过:
更改数组 nums ,使 nums 的前 k 个元素包含唯一元素,并按照它们最初在 nums 中出现的顺序排列。nums 的其余元素与 nums 的大小不重要。
返回 k 。
判题标准:
系统会用下面的代码来测试你的题解:
int[] nums = […]; // 输入数组
int[] expectedNums = […]; // 长度正确的期望答案
int k = removeDuplicates(nums); // 调用
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums[i] == expectedNums[i];
}
如果所有断言都通过,那么您的题解将被 通过。
示例 1:
输入:nums = [1,1,2]
输出:2, nums = [1,2,_]
解释:函数应该返回新的长度 2 ,并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。
示例 2:
输入:nums = [0,0,1,1,1,2,2,3,3,4]
输出:5, nums = [0,1,2,3,4]
解释:函数应该返回新的长度 5 , 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。
提示:
1 <= nums.length <= 3 * 104
-104 <= nums[i] <= 104
nums 已按 非严格递增 排列
解答
class Solution:def removeDuplicates(self, nums: List[int]) -> int:i = 0n = len(nums)for j in range(n):if nums[i] == nums[j]:continuei += 1nums[i] = nums[j]return i+1
最后,我写了一篇MySQL教程,里面详细的介绍了MySQL的基本概念以及操作指令等内容,欢迎阅读!
MySQL数据库万字保姆级教程
相关文章:
第26题删除有序数组中的重复项(Python))
力扣(leetcode)第26题删除有序数组中的重复项(Python)
26.删除有序数组的重复项 题目链接:26.删除有序数组的重复项 给你一个非严格递增排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 …...
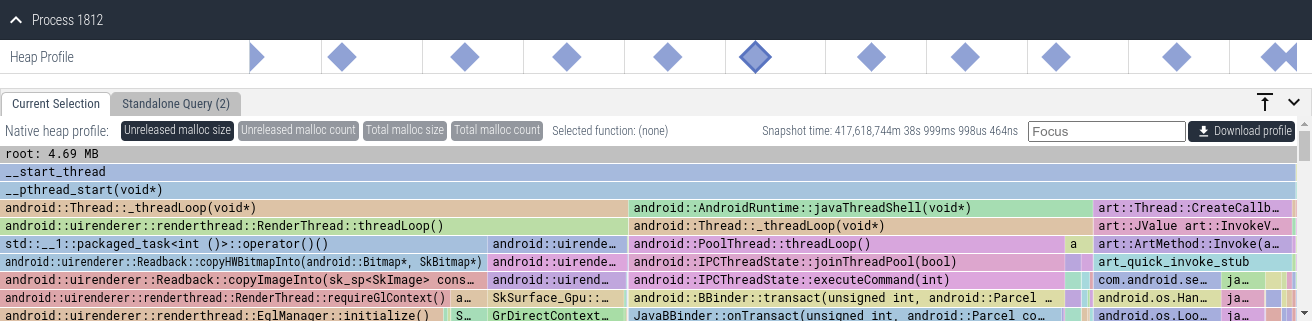
【内存泄漏】内存泄漏及常见的内存泄漏检测工具介绍
内存泄漏介绍 什么是内存泄漏 内存泄漏是指程序分配了一块内存(通常是动态分配的堆内存),但在不再需要这块内存的情况下未将其释放。内存泄漏会导致程序浪费系统内存资源,持续的内存泄漏还导致系统内存的逐渐耗尽,最…...
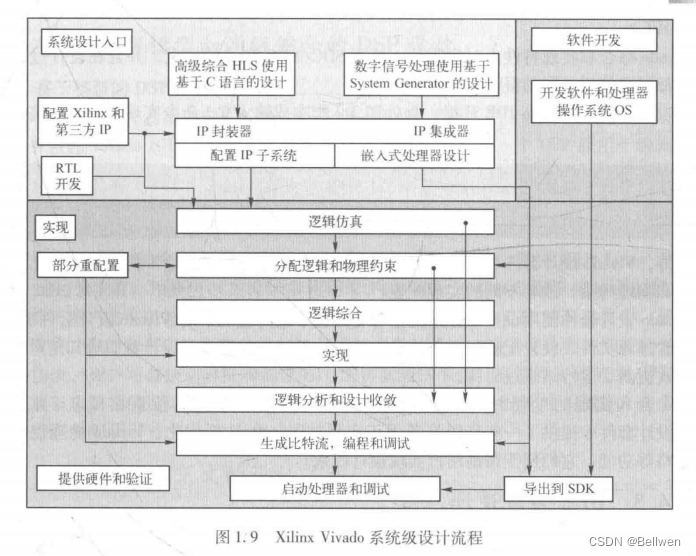
FPGA-ZYNQ-7000 SoC在嵌入式系统中的优势
FPGA-ZYNQ-7000 SoC在嵌入式系统中的优势 本章节主要参考书籍《Xilinx Zynq-7000 嵌入式系统设计与实现 基于ARM Cortex-A9双核处理器和Vivado的设计方法 (何宾,张艳辉编著)》 本章节主要讲述FPGA-ZYNQ-7000 SoC在嵌入式系统中的优势,学习笔…...

如何在Vue3中实现无缝热重载:提升你的开发效率
Vue3中的热重载(Hot Module Replacement,简称HMR)是一种开发时的功能,它允许开发者在不刷新整个页面的情况下,实时替换、添加或删除模块。这意味着当你对Vue组件进行修改并保存时,这些更改会立即反映在浏览…...
盒子 Box
UVa1587 思路: 1.输入每个面的长宽并将每个面较长的一边放在前面 2.判断是否存在三对面分别相等 3.判断是否存在三组四棱相等 #include <stdio.h> #include <stdlib.h> #define maxn 100int cmp(const void* e1, const void* e2) {return (int)(*(d…...

uni-app附件下载预览 并解决打开附件时黑屏
// 预览附件perviewFile(file) {console.log(点击附件, file)var strfile.previewUrlvar filTypestr.split(.)console.log(filType,filType)uni.downloadFile({url: success: function(res) {console.log(打开文档成功, res);if (res.statusCode 200) {uni.saveFile({tempFile…...

卸载了Visual Studio后,在vscode中执行npm i或npm i --force时报错,该怎么解决?
卸载了Visual Studio后,在vscode中执行npm i或npm i --force时报错,该怎么解决? 报错内容:原因解决办法 报错内容: npm ERR! code 1 npm ERR! path E:\VScode\codeDate\yugan\node_modules\node-sass npm ERR! command failed np…...
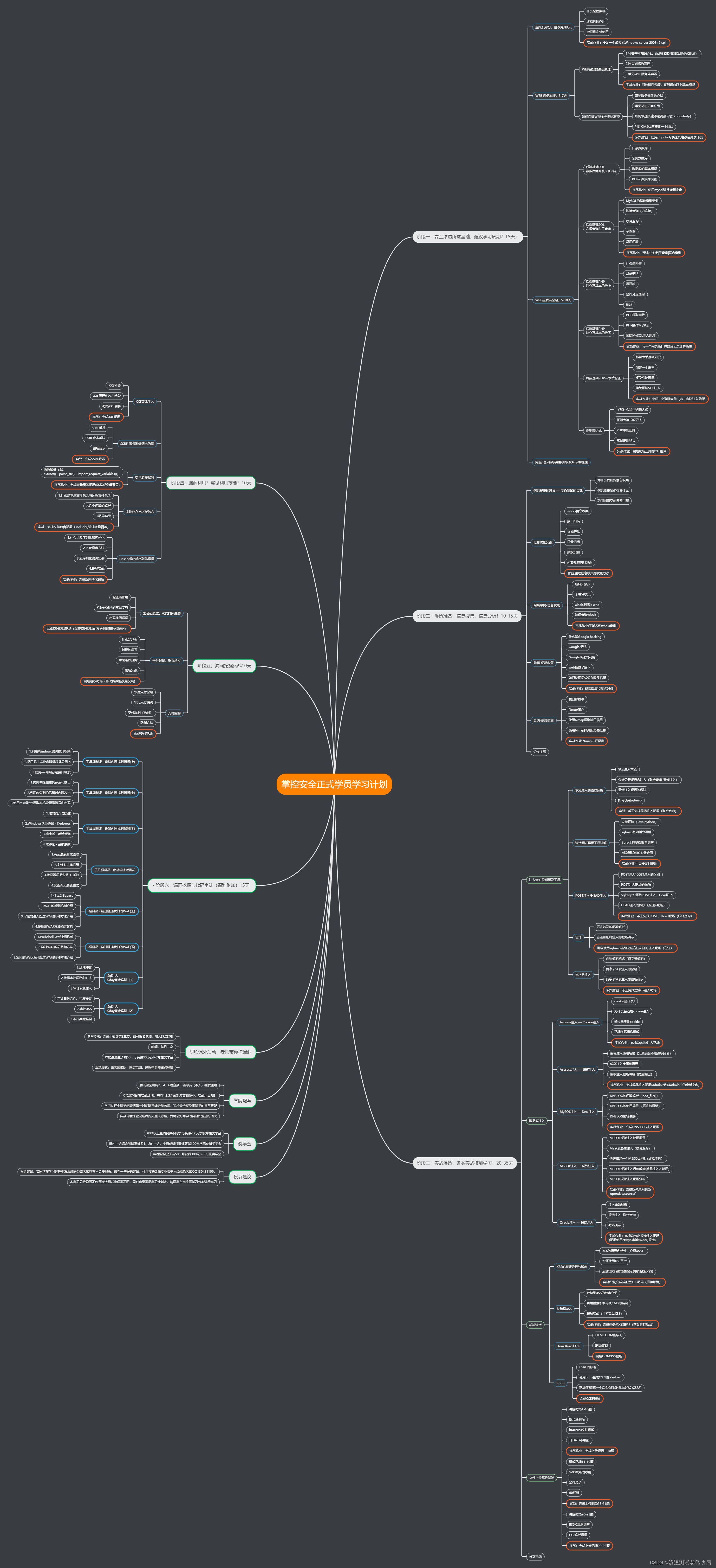
渗透测试 | 信息收集常用方法合集
目录 一、关于域名 1.子域名收集 a.搜索引擎查找 b.在线查询 c.工具 d.SSL/TLS证书查询 2.端口型站点收集 3.目录文件扫描 a.目录扫描工具 b.github搜索 c.google搜索 d.在线网站 e.文件接口工具 4.旁站和C段 a.旁站查询 b.C段查询 5.网站技术架构信息 a.基础…...

使用 ElementUI 组件构建无边框 Window 桌面应用(WinForm/WPF)
生活不可能像你想象得那么好,但也不会像你想象得那么糟。 我觉得人的脆弱和坚强都超乎自己的想象。 有时,我可能脆弱得一句话就泪流满面;有时,也发现自己咬着牙走了很长的路。 ——莫泊桑 《一生》 一、技术栈 Vite + Vue3 + TS + ElementUI(plus) + .NET Framework 4.7.2…...

JavaScript中数组的方法和函数作用域问题
1 -函数作用域问题-: 函数的外层作用域,在函数创建时就已确定,和函数的调用位置无关 var name 嘿嘿;// 函数的外层作用域,在函数创建时就已确定,和函数的调用位置无关// JS中的作用域被称为 词法作用域function fn() {console.…...

nodejs设置x-xss-protection解决xss问题
在Node.js中设置X-XSS-Protection可以通过使用helmet库来完成。 首先,确保已经安装了helmet库。如果没有安装,可以运行以下命令进行安装: npm install helmet --save 然后,在你的Node.js应用程序中引入并配置helmet库ÿ…...

C/C++不同整数类型的区别
在C/C中涉及的整数相关的类型大致有如下几种: char、unsigned charshort、unsigned shortint、unsigned intlong、unsigned longlong long、unsigned long longint8_t、uint8_tint32_t、uint32_tint64_t、uint64_tDWORDDWORD32、DWORD64size_t、ssize_tSIZE_T、SSI…...

如何理解JDK、JRE、JVM区别与联系
摘要:JDK是 Java 语言的软件开发工具包(SDK)。在JDK的安装目录下有一个jre目录,里面有两个文件夹bin和lib,在这里可以认为bin里的就是jvm,lib中则是jvm工作所需要的类库,而jvm和 lib合起来就称为jre。 一、JDK JDK(Ja…...

用友GRP-U8 SmartUpload01 文件上传漏洞
漏洞描述 用友GRP-U8行政事业内控管理软件是一款专门针对行政事业单位开发的内部控制管理系统,旨在提高内部控制的效率和准确性。该软件/u8qx/SmartUpload01.jsp接口存在文件上传漏洞,未经授权的攻击者可通过此漏洞上传恶意后门文件,从而获取…...
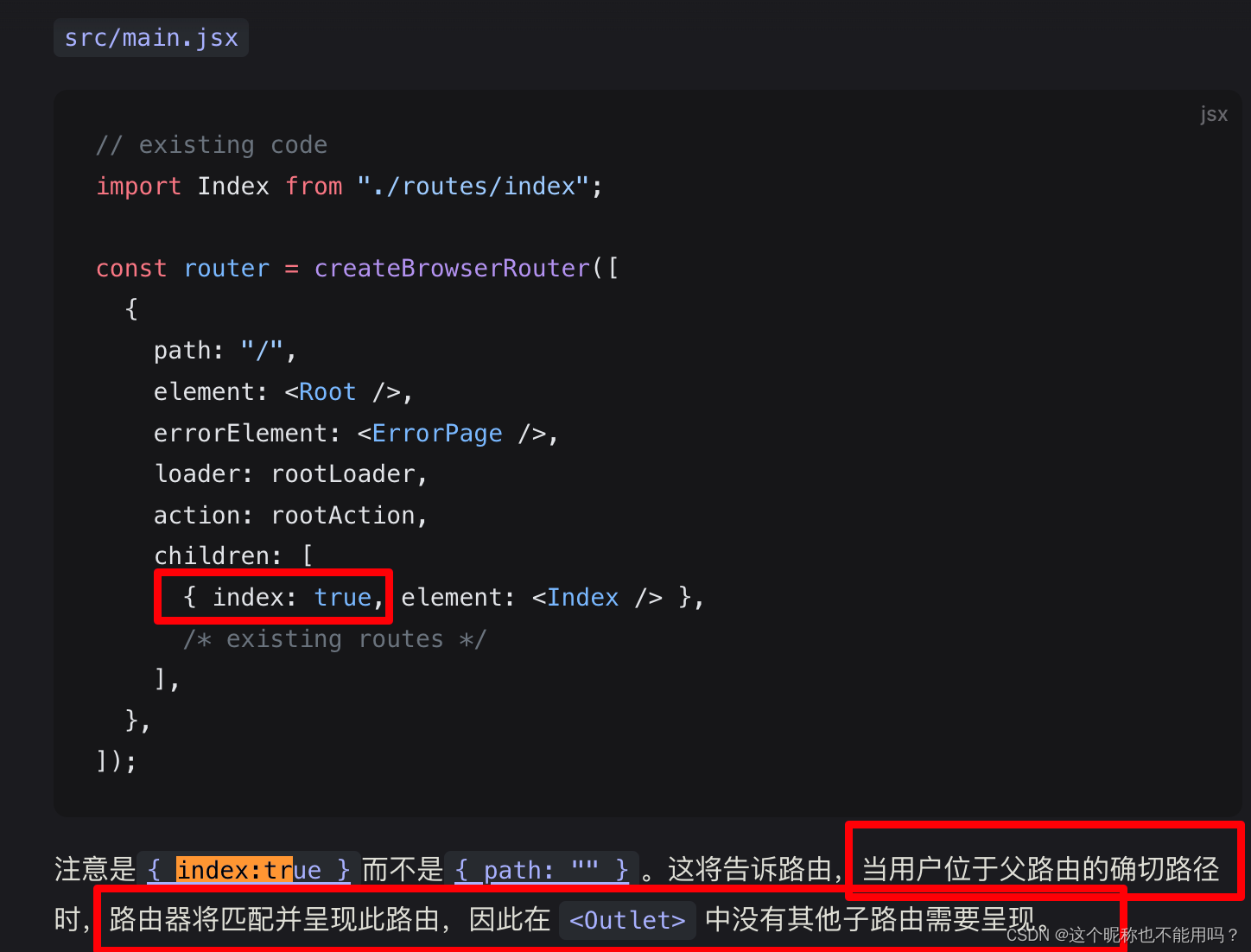
react 路由v6
这里是区别:V5 vs V6 这里是官网:可以查看更多高级属性 一、基本使用: 1、配置文件 src/routes/index import React from "react";const Home React.lazy(() > import("../Pages/Home")); const About React.laz…...

rpc【通义】rpc原理【gpt】
一 rpc RPC(Remote Procedure Call,远程过程调用)是一种编程技术,它允许在分布式系统中的一个程序像调用本地函数一样调用另一个程序(位于不同的机器或进程中)的函数或方法。RPC的主要目标是隐藏网络通信的…...

Leetcode 2973. Find Number of Coins to Place in Tree Nodes
Leetcode 2973. Find Number of Coins to Place in Tree Nodes 1. 解题思路2. 代码实现 题目链接:2973. Find Number of Coins to Place in Tree Nodes 1. 解题思路 这道题思路上其实挺简单的,就是一个遍历的思路,找到每一个点对应的子树当…...
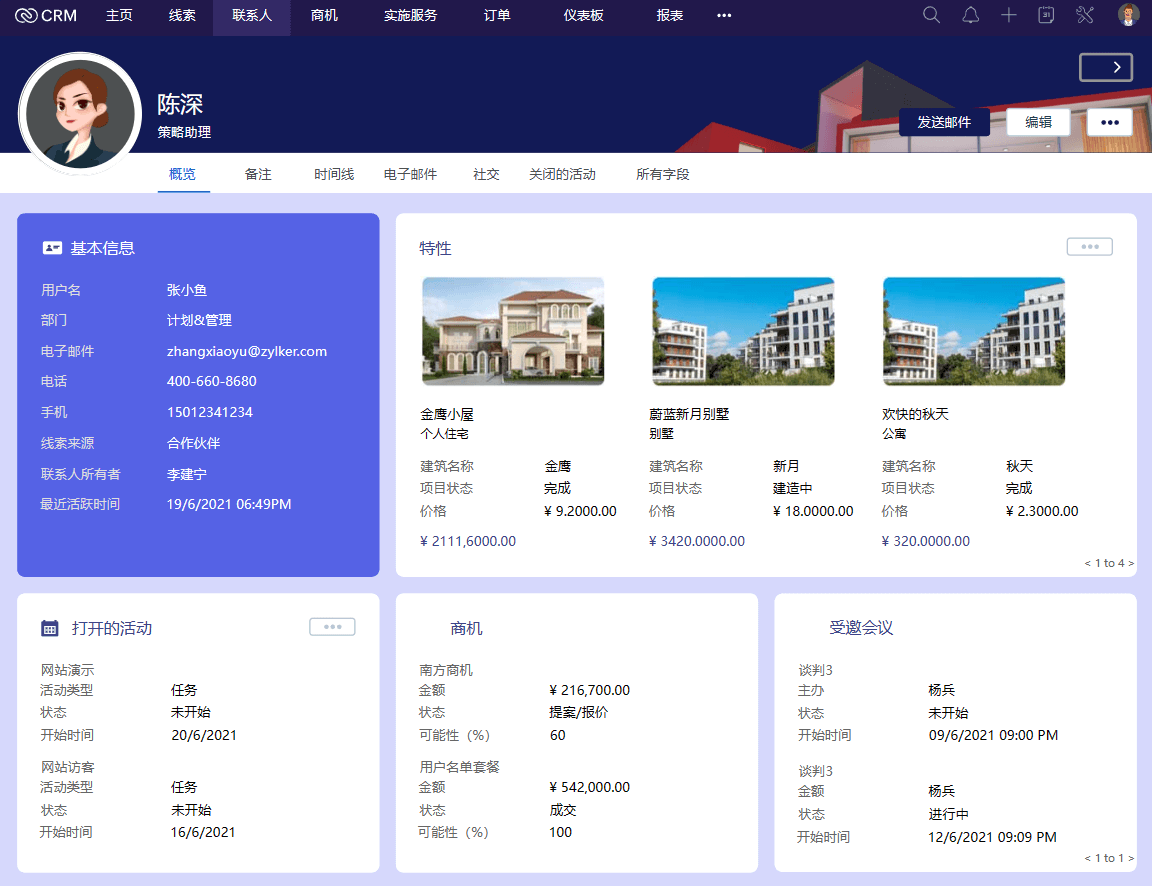
如何调动销售人员使用CRM的积极性?
CRM系统在销售人员眼中是流程监管工具也是单调枯燥的操作空间,如何让销售爱上CRM系统?1.让CRM简化销售工作;2.智能提醒销售各项事务;3.让CRM界面更加丰富多彩,通过这些方法帮助销售经理轻松管理团队,销售对…...

数值分析期末复习
第一章 科学计算 误差 解题步骤 x : 真实值 x:真实值 x:真实值 x ∗ : 近似值 x^*:近似值 x∗:近似值 先求绝对误差 e ∗ e^* e∗: x − x ∗ x - x^* x−x∗ 绝对误差限是 ∣ x − x ∗ ∣ ≤ ε |x - x^{*}| \le \varepsilon ∣x−x∗∣≤ε 求相对误差限: ∣ x − x ∗…...

k8s的探针
一、探针原理 分布式系统和微服务体系结构的挑战之一是自动检测不正常的应用程序,并将请求(request)重新路由到其他可用系统,恢复损坏的组件。健康检查是应对该挑战的一种可靠方法。使用 Kubernetes,可以通过探针配置运…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...
