统计直线上2个点的分布占比
直线上有6个格子,向格子里扔2个石子,共有5种可能。
| 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 1 |
第1种两个石子是连着的,共有5个
| 1 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 | 1 |
第2种两个石子间隔1个格子,有4个
| 1 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
两个石子间距为2,有3个
| 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 |
两个石子间距为3,有2个
| 1 | 0 | 0 | 0 | 0 | 1 |
两个石子间距4,只有1个。一共只有这15种可能。
| 15 | % |
| 5 | 0.333333 |
| 4 | 0.266667 |
| 3 | 0.2 |
| 2 | 0.133333 |
| 1 | 0.066667 |
所以两个石子间距越大,发生的概率越小。所以随机的向这6个格子里扔2个石子,有1/3的概率两个石子是连着的。
( A, B )---1*30*2---( 1, 0 )( 0, 1 )
做一个网络分类A和B,让B全是0,A训练集只有6张图片。
| A | 迭代次数 | ||||||
| 1 | 1 | 0 | 0 | 0 | 0 | 58609.84 |
首先分类1,1,0,0,0,0,得到平均收敛迭代次数为58609,因为差值结构的行可以按照1-2-3-4-5-6-1的顺序变换,所以
| 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 1 |
第一组5个结构的迭代次数都相同。
用同样的办法测量第2组和第3组
| A | 迭代次数 | ||||||
| 1 | 1 | 0 | 0 | 0 | 0 | 58609.84 | |
| 1 | 0 | 1 | 0 | 0 | 0 | 61017.26 | |
| 1 | 0 | 0 | 1 | 0 | 0 | 63229.15 |
得到表格,很明显间距是0,1,2的3组的迭代次数是逐渐增加的。因为间距是0,1,2的3组发生的概率是由大到小的,所以这里的迭代次数与结构A的发生概率成反比。发生概率越大,迭代次数越小。越容易被随机到,越容易收敛。
| 1 | 1 | 0 | 0 | 0 | 0 | ||
| 1 | 0 | 0 | 0 | 0 | 1 |
但在神经网络中因为差值结构的循环节长度是6,所以间距为0和间距为4的迭代次数是一样的。
| 1 | 0 | 1 | 0 | 0 | 0 | ||
| 1 | 0 | 0 | 0 | 1 | 0 |
同样间距为1和间距为3的迭代次数也是相同的。
所以只有3组不同的迭代次数。
所以网络
( A, B )---1*30*2---( 1, 0 )( 0, 1 )
的收敛过程等价于随机的向直线上的6个格子里扔石子,有的结构更容易收敛是因为这个结构在搜索范围内天然的占比更大。
随机验算,随机扔了500次,1000次
| 组合 | |||||||
| 15 | % | 500 | % | 1000 | % | ||
| 5 | 0.333333 | 172 | 0.344 | 323 | 0.323 | ||
| 4 | 0.266667 | 131 | 0.262 | 276 | 0.276 | ||
| 3 | 0.2 | 94 | 0.188 | 200 | 0.2 | ||
| 2 | 0.133333 | 66 | 0.132 | 137 | 0.137 | ||
| 1 | 0.066667 | 37 | 0.074 | 64 | 0.064 |
相关文章:

统计直线上2个点的分布占比
直线上有6个格子,向格子里扔2个石子,共有5种可能。 1 1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 第1种两个石子是连着的,共有5个 1 0 1 0 0 0 0 1 0 1 0 0 0 0 1 0 1 0 …...
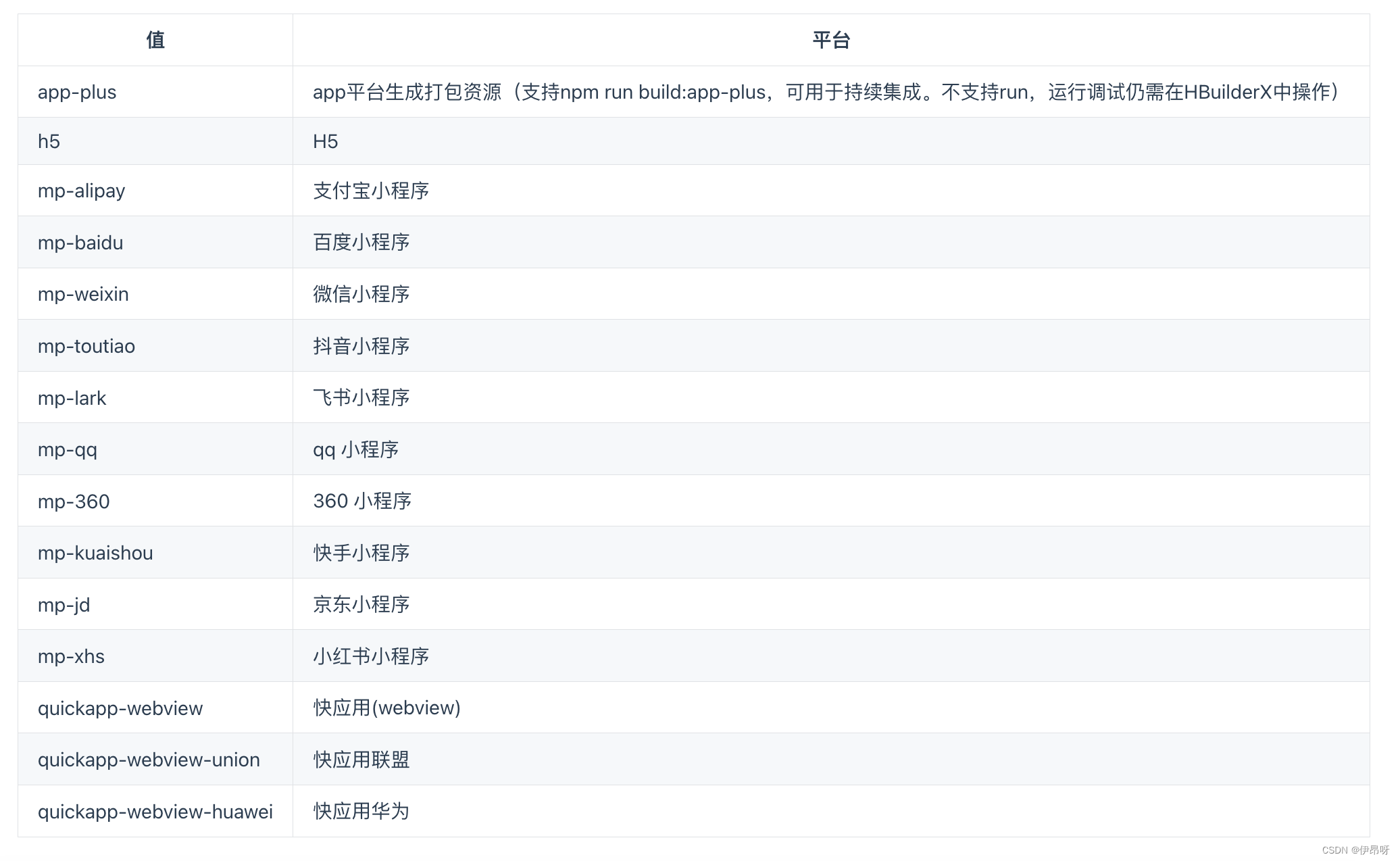
uniapp创建/运行/发布项目
1、产生背景----跨平台应用框架 在移动端各大App盛行的时代,App之间的竞争也更加激烈,他们执着于让一个应用可以做多个事情 所以就应运而生了小程序,微信小程序、支付宝小程序、抖音小程序等等基于App本身的内嵌类程序。 但是各大App他不可…...

洛谷 P2367 语文成绩 刷题笔记
P2367 语文成绩 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 差分 令a[i]为b[i]数组的前缀和 a[n]b[1]b[2]b[3].....b[n]; a[n-1]b[1]b[2]b[3].....b[n-1]; 构造差分数组 b[i]a[i]-a[i-1]; 有什么好处 当我们想对a[l]--a[r]范围内所有数据加上一个数x 不必循环 for(i…...
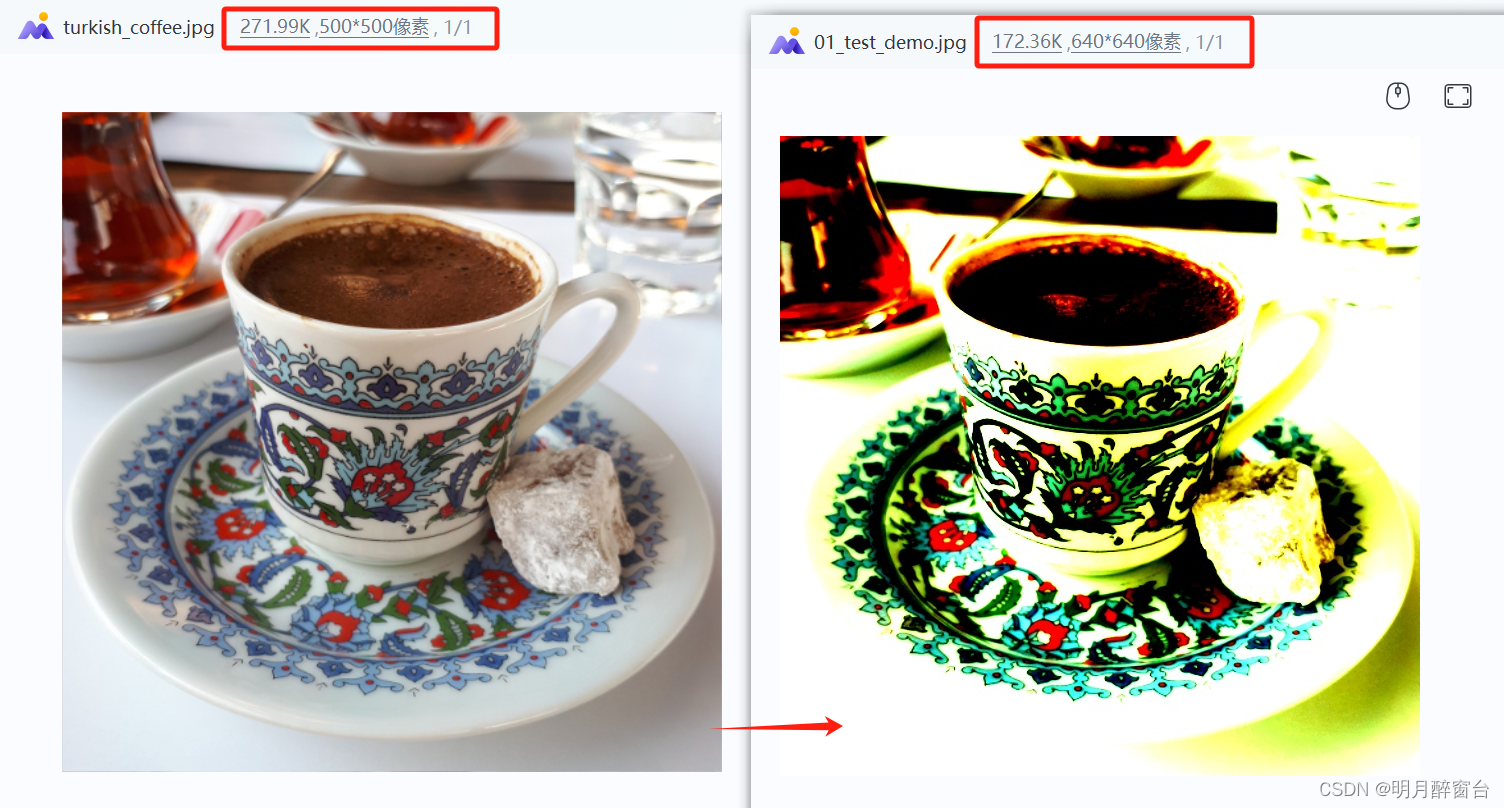
Opencv_CUDA实现推理图像前处理与后处理
Opencv_CUDA实现推理图像前处理与后处理 通过trt 或者 openvino部署深度学习算法时,往往会通过opencv的Mat及算法将图像转换为固定的格式作为输入openvino图像的前后处理后边将在单独的文章中写出今晚空闲搜了一些opencv_cuda的使用方法,在此总结一下前…...

Android.bp 和 Android.mk 的对应关系
参考 Soong 构建系统 Android.mk 转为 Android.bp 没有分支、循环等流程控制的简单的 Android.mk ,可以通过 androidmk 命令转化为 Android.bp source 、lunch 之后执行即可。 androidmk Android.mk > Android.bp对应关系 Android 13 ,build/soon…...

力扣-收集足够苹果的最小花园周长[思维+组合数]
题目链接 题意: 给你一个用无限二维网格表示的花园,每一个 整数坐标处都有一棵苹果树。整数坐标 (i, j) 处的苹果树有 |i| |j| 个苹果。 你将会买下正中心坐标是 (0, 0) 的一块 正方形土地 ,且每条边都与两条坐标轴之一平行。 给你一个整…...

【C语言】自定义类型:结构体深入解析(三)结构体实现位段最终篇
文章目录 📝前言🌠什么是位段?🌉 位段的内存分配🌉VS怎么开辟位段空间呢?🌉位段的跨平台问题🌠 位段的应⽤🌠位段使⽤的注意事项🚩总结 📝前言 本…...
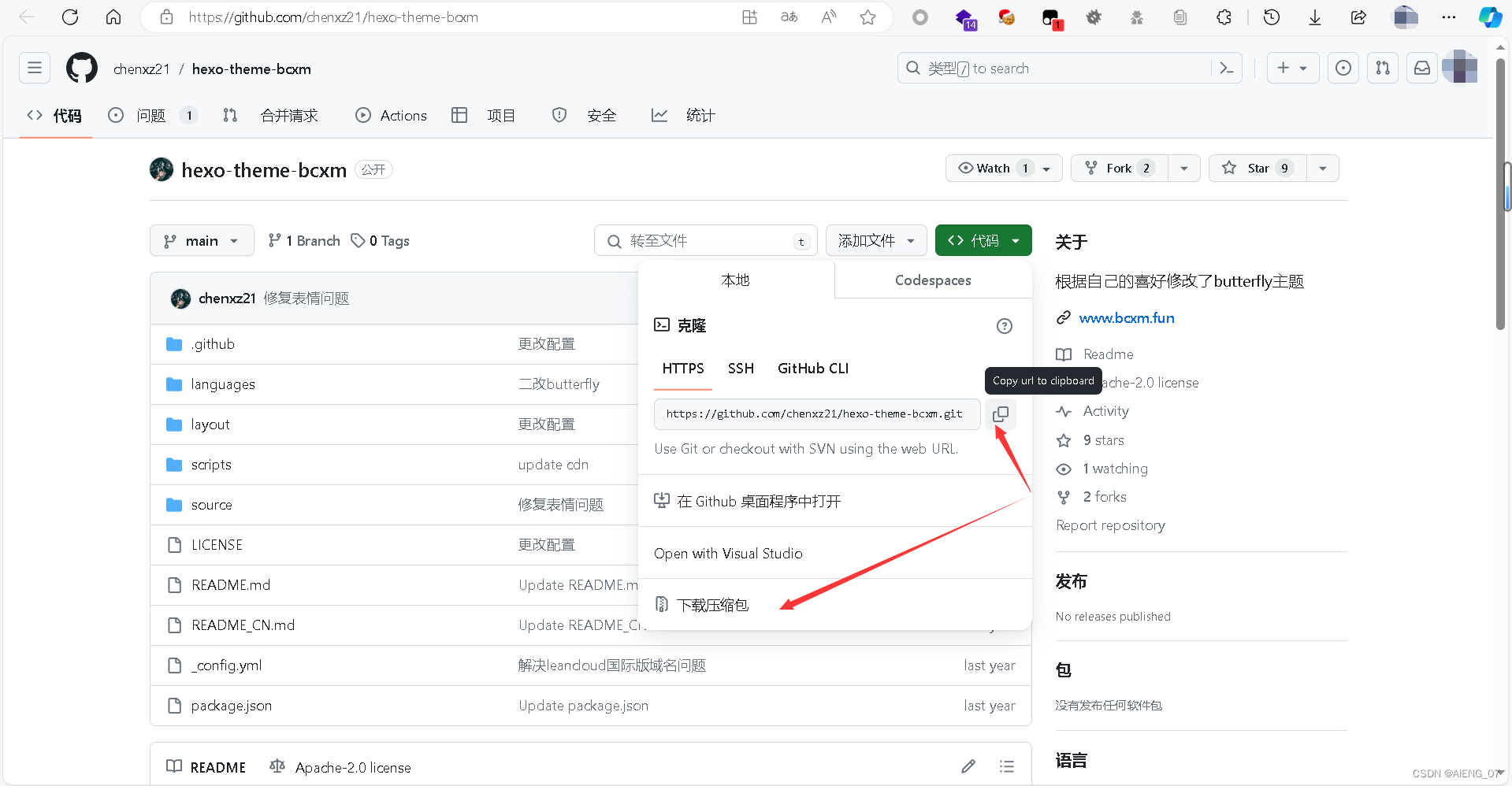
基于Hexo+GitHub Pages 的个人博客搭建
基于HexoGitHub Pages 的个人博客搭建 步骤一:安装 Node.js 和 Git步骤二:创建Github Pages 仓库步骤二:安装 Hexo步骤三:创建 Hexo 项目步骤四:配置 Hexo步骤五:创建新文章步骤六:生成静态文件…...

7. 结构型模式 - 代理模式
亦称: Proxy 意图 代理模式是一种结构型设计模式, 让你能够提供对象的替代品或其占位符。 代理控制着对于原对象的访问, 并允许在将请求提交给对象前后进行一些处理。 问题 为什么要控制对于某个对象的访问呢? 举个例子ÿ…...

挑战Python100题(6)
100+ Python challenging programming exercises 6 Question 51 Define a class named American and its subclass NewYorker. Hints: Use class Subclass(ParentClass) to define a subclass. 定义一个名为American的类及其子类NewYorker。 提示:使用class Subclass(Paren…...

gin实现登录逻辑,包含cookie,session
users/login.html {{define "users/login.html"}} <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>登录页面</title> </head> <body><form method"post" a…...
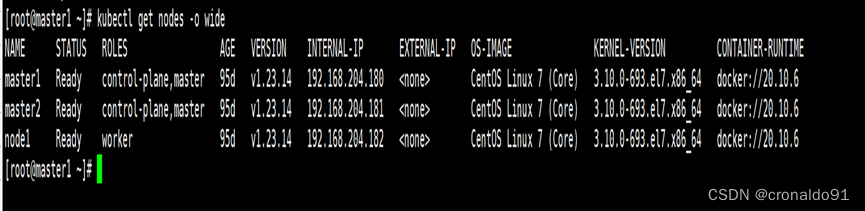
云原生Kubernetes:K8S集群版本升级(v1.22.14 - v1.23.14)
目录 一、理论 1.K8S集群升级 2.环境 3.升级集群(v1.23.14) 4.验证集群(v1.23.14) 二、实验 1. 环境 2.升级集群(v1.23.14) 2.验证集群(v1.23.14) 一、理论 1.K8S集群升级 …...
编程-位运算详解)
C++面向对象(OOP)编程-位运算详解
本文主要介绍原码、位运算的种类,以及常用的位运算的使用场景。 目录 1 原码、反码、补码 2 有符号和无符号数 3 位运算 4 位运算符使用规则 4.1 逻辑移位和算术移位 4.1.1 逻辑左移和算法左移 4.1.2 逻辑右移和算术右移 4.1.3 总结 4.2 位运算的应用场景 …...

linux运行服务提示报错/usr/bin/java: 没有那个文件或目录
如果是直接从官网下载的jdk解压安装,那么/usr/bin/没有java的软连接,即/usr/bin/java,所以即使在/etc/profile中配置了jdk的环境变量也没用,识别不到。 方法一:用java的执行路径配置/usr/bin/java软连接(优…...

一篇文章教会你数据仓库之详解拉链表怎么做
前言 本文将会谈一谈在数据仓库中拉链表相关的内容,包括它的原理、设计、以及在我们大数据场景下的实现方式。 全文由下面几个部分组成: 先分享一下拉链表的用途、什么是拉链表。通过一些小的使用场景来对拉链表做近一步的阐释,以及拉链表和…...

C/S医院检验LIS系统源码
一、检验科LIS系统概述: LIS系统即实验室信息管理系统。LIS系统能实现临床检验信息化,检验科信息管理自动化。其主要功能是将检验科的实验仪器传出的检验数据经数据分析后,自动生成打印报告,通过网络存储在数据库中ÿ…...
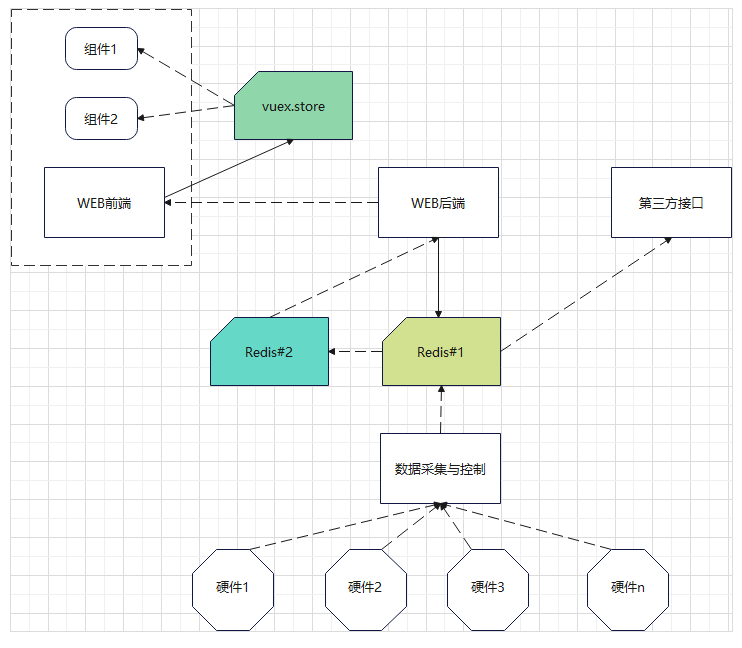
项目应用多级缓存示例
前不久做的一个项目,需要在前端实时展示硬件设备的数据。设备很多,并且每个设备的数据也很多,总之就是数据很多。同时,设备的刷新频率很快,需要每2秒读取一遍数据。 问题来了,我们如何读取数据,…...

音视频技术开发周刊 | 325
每周一期,纵览音视频技术领域的干货。 新闻投稿:contributelivevideostack.com。 AI读心术震撼登顶会!模型翻译脑电波,人类思想被投屏|NeurIPS 2023 在最近举办的NeurIPS大会上,研究人员展示了当代AI更震撼…...
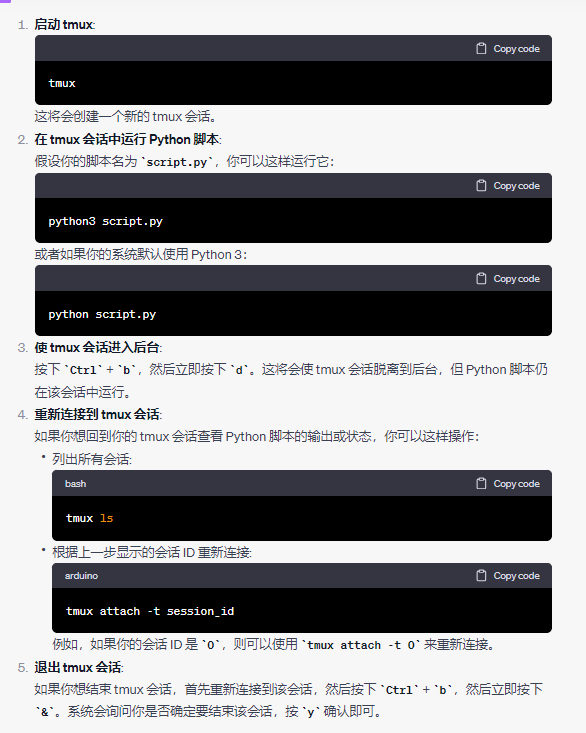
量化服务器 - 后台挂载运行
服务器 - 后台运行 pip3命令被kill 在正常的pip命令后面加上 -no-cache-dir tmux 使用教程 https://codeleading.com/article/40954761108/ 如果你希望在 tmux 中后台执行一个 Python 脚本,你可以按照以下步骤操作: 启动 tmux: tmux这将会创建一个新…...
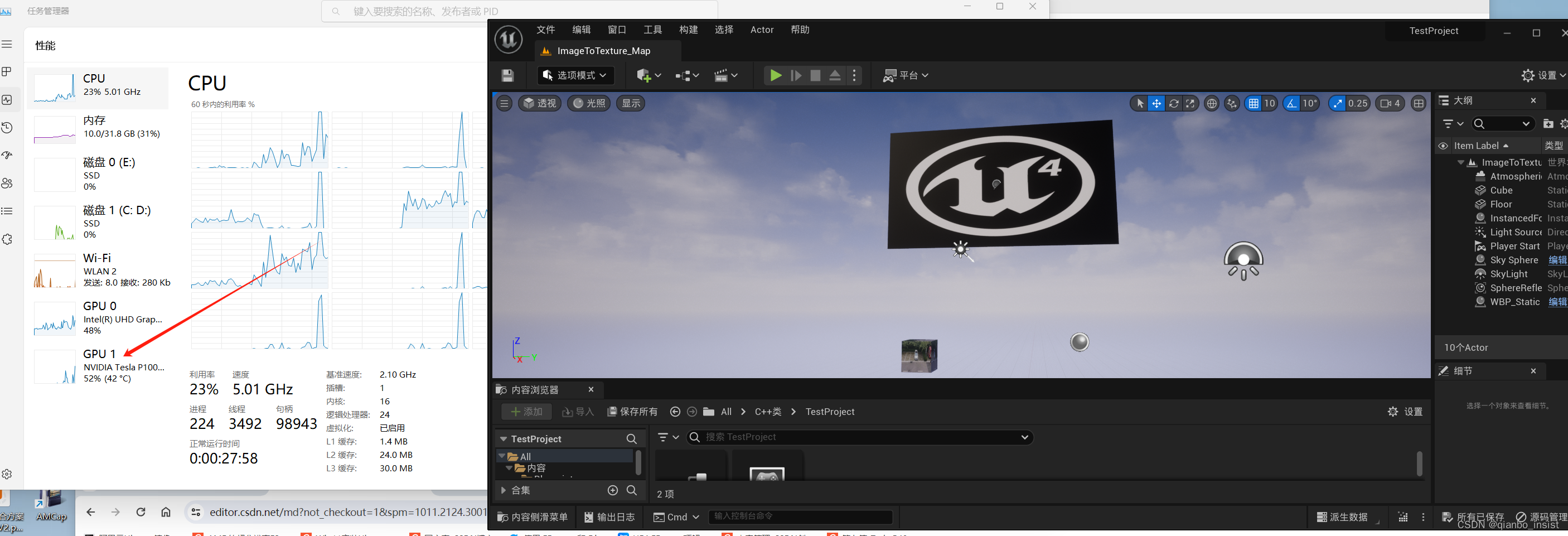
使用tesla gpu 加速大模型,ffmpeg,unity 和 UE等二三维应用
我们知道tesla gpu 没有显示器接口,那么在windows中怎么使用加速unity ue这种三维编辑器呢,答案就是改变注册表来加速相应的三维渲染程序. 1 tesla gpu p40 p100 加速 在windows中使用regedit 来改变 核显配置, 让p100 p40 等等显卡通过核显…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...

性能优化中,多面体模型基本原理
1)多面体编译技术是一种基于多面体模型的程序分析和优化技术,它将程序 中的语句实例、访问关系、依赖关系和调度等信息映射到多维空间中的几何对 象,通过对这些几何对象进行几何操作和线性代数计算来进行程序的分析和优 化。 其中࿰…...

SOC-ESP32S3部分:30-I2S音频-麦克风扬声器驱动
飞书文档https://x509p6c8to.feishu.cn/wiki/SKZzwIRH3i7lsckUOlzcuJsdnVf I2S简介 I2S(Inter-Integrated Circuit Sound)是一种用于传输数字音频数据的通信协议,广泛应用于音频设备中。 ESP32-S3 包含 2 个 I2S 外设,通过配置…...
