Large-Precision Sign using PBS
参考文献:
- [CLOT21] Chillotti I, Ligier D, Orfila J B, et al. Improved programmable bootstrapping with larger precision and efficient arithmetic circuits for TFHE[C]//Advances in Cryptology–ASIACRYPT 2021: 27th International Conference on the Theory and Application of Cryptology and Information Security, Singapore, December 6–10, 2021, Proceedings, Part III 27. Springer International Publishing, 2021: 670-699.
- [LMP22] Liu Z, Micciancio D, Polyakov Y. Large-precision homomorphic sign evaluation using FHEW/TFHE bootstrapping[C]//International Conference on the Theory and Application of Cryptology and Information Security. Cham: Springer Nature Switzerland, 2022: 130-160.
文章目录
- Homomorphic Floor Function
- Using 2 PBS
- Using 3 PBS
- PBS of Arbitrary Function
- Homomorphic Digit Decomposition
- Parameter Selection
[CLOT21] 提出了 WoP-PBS,它基于事实 ( − 1 ) ⋅ ( − m ) = m (-1) \cdot (-m)=m (−1)⋅(−m)=m,先将 m m m 扩展为 β ∥ m \beta\|m β∥m,然后使用 GenPBS 分别计算出 ( − 1 ) β ⋅ f ( m ) (-1)^\beta \cdot f(m) (−1)β⋅f(m) 和 ( − 1 ) β (-1)^\beta (−1)β,最后使用 FV-like 同态乘法,将它们组合成 f ( m ) f(m) f(m)。这需要底层的 LWE 同时支持加法和乘法,并且同态乘法导致了噪声增长。因此,模数(正确性)和维度(安全性)都会相应的变大,导致它比一般的 FHEW/TFHE 的效率更至少一倍。
[LMP22] 也是将 m m m 扩展到 β ∥ m \beta\|m β∥m,单它首先将 β \beta β 消除掉使之成为 0 ∥ m 0\|m 0∥m,接着使用原始的 PBS 就可以计算出正确的 f ( m ) f(m) f(m)。在这个过程中,并不需要使用同态乘法,因此它的噪声就是 PBS 本身的噪声,常规的参数就足够使用。
Homomorphic Floor Function
首先,[LMP22] 研究了如何对于高精度 LWE 密文执行自举。这里的 “精度” 指的是 MSD 编码的消息的比特长度。我们先给出一些参数定义:
- LWE:
- 维度 n n n,不需要是二的幂
- 模数 Q Q Q,是二的幂,用于 LWE 同态运算
- 模数 q q q,是二的幂,用于 PBS 自举
- 缩放因子 α \alpha α,是二的幂,用于纠错
- 噪声界 β \beta β,是二的幂
- ACC:
- 多项式长度 N N N,是二的幂
- RLWE 密文模数 Q ′ Q' Q′,是满足 2 N ∣ Q ′ − 1 2N \mid Q'-1 2N∣Q′−1 的素数
- 输入 LWE 密文模数 q ∣ 2 N q \mid 2N q∣2N
- 输出 LWE 密文模数 Q Q Q
FHEW/TFHE 要求 LWE 的密文模数满足 Q ∣ 2 N Q \mid 2N Q∣2N,随着明文精度的增加( k k k 比特),多项式长度 N N N 指数级增加( 2 k 2^k 2k 倍)。对于通常的参数集 N = 1024 / 2048 N=1024/2048 N=1024/2048,只能支持至多 3 , 4 3,4 3,4 比特的明文精度。[LMP22] 为了计算高精度的 Sign 函数,通过不断移除 LSD(保持 MSB 不变),直到密文模数 Q Q Q 倍缩减到 q q q 规模,从而可以使用常规参数集执行 PBS。
这个过程中,一个关键步骤是同态 Floor 函数。假设 LWE 密文 ( c , d ) ∈ Z Q n + 1 (c,d) \in \mathbb Z_Q^{n+1} (c,d)∈ZQn+1 的相位是:
ψ = α ⋅ m + e ( m o d Q ) \psi = \alpha \cdot m + e \pmod Q ψ=α⋅m+e(modQ)
其中 ∣ e ∣ ≤ β ≪ q |e| \le \beta \ll q ∣e∣≤β≪q, m ∈ Z Q / α m \in \mathbb Z_{Q/\alpha} m∈ZQ/α,根据不同的场景 α \alpha α 选取不同的值。
注意到 Q > q > α Q>q>\alpha Q>q>α 都是二的幂次。如果我们将 LWE 密文模掉 q q q,获得的 ( a , b ) ∈ Z q n + 1 (a,b) \in \mathbb Z_q^{n+1} (a,b)∈Zqn+1:
[ m ′ ] q = α ⋅ [ m ] q / α + e ( m o d q ) [m']_q = \alpha \cdot [m]_{q/\alpha} + e \pmod q [m′]q=α⋅[m]q/α+e(modq)
使用 PBS 将它提升回 ( a ′ , b ′ ) ∈ Z Q n + 1 (a',b') \in \mathbb Z_Q^{n+1} (a′,b′)∈ZQn+1,并从原始密文中把它减掉,就清除了 m m m 的最低 log q / α \log{q/\alpha} logq/α 比特。密文 ( c ′ , d ′ ) (c',d') (c′,d′) 的相位是:
ψ ′ = α ⋅ ( ⌊ α q m ⌋ ⋅ q α ) + e ′ ( m o d Q ) \psi' = \alpha \cdot \left(\left\lfloor \frac{\alpha}{q} m \right\rfloor \cdot \frac{q}{\alpha} \right) + e' \pmod Q ψ′=α⋅(⌊qαm⌋⋅αq)+e′(modQ)
现在,我们可以把 α , Q \alpha,Q α,Q 同时缩小 q / α q/\alpha q/α 倍,得到的密文 ( c ′ ′ , d ′ ′ ) ∈ Z ( α / q ) ⋅ Q n + 1 (c'',d'') \in \mathbb Z_{(\alpha/q) \cdot Q}^{n+1} (c′′,d′′)∈Z(α/q)⋅Qn+1 相位的 MSB 保持和 ( c , d ) ∈ Z Q n + 1 (c,d) \in \mathbb Z_Q^{n+1} (c,d)∈ZQn+1 的一样。
我们将这个长度 log ( q / α ) \log(q/\alpha) log(q/α) 的小块明文称为 LSD,我们的目标是将它清零。然而,函数 f : m ∈ Z q / α ↦ m ∈ Z Q / α f:m \in \mathbb Z_{q/\alpha} \mapsto m \in \mathbb Z_{Q/\alpha} f:m∈Zq/α↦m∈ZQ/α 并非反循环的,导致了原始的 PBS 无法实现从 ( a , b ) (a,b) (a,b) 到 ( a ′ , b ′ ) (a',b') (a′,b′) 的自举过程。[LMP22] 给出了两种实现,通过 2 , 3 2,3 2,3 次 PBS 来实现它。用到的三个函数为:

为了构造 LUT 的方便,下面的推导中总是使得 PBS 输入的密文噪声是正整数,范围是 [ 0 , 2 β ) [0,2\beta) [0,2β)。这可通过 ( c , d ) → ( c , d + β ) (c,d) \to (c,d+\beta) (c,d)→(c,d+β) 来实现。只要满足 α ≥ 2 β \alpha \ge 2\beta α≥2β,就可以准确解密。FHEW/TFHE 中的 LWE 私钥 s ∈ { 0 , ± 1 } n s \in \{0,\pm1\}^n s∈{0,±1}n 服从三元分布。
Using 2 PBS
[LMP22] 的第一个方法:使用两次 PBS,但是对于噪声的约束较强, α ≥ 4 β \alpha \ge 4\beta α≥4β
基本思路:分别提取 ( [ c ] q , [ d ] q ) ([c]_q,[d]_q) ([c]q,[d]q) 相位(加密了 LSD)的 MSB 和其他位置,
- 先提取 ( [ c ] q , [ d ] q ) ([c]_q,[d]_q) ([c]q,[d]q) 的 MSB,将它从 ( c , d ) ∈ Z Q n + 1 (c,d) \in \mathbb Z_Q^{n+1} (c,d)∈ZQn+1 中移除。现在 ( [ c ′ ] q , [ d ′ ] q ) ([c']_q,[d']_q) ([c′]q,[d′]q) 的相位只位于半个环面上。
- 再提取 ( [ c ′ ] q , [ d ′ ] q ) ([c']_q,[d']_q) ([c′]q,[d′]q) 的消息,将它从 ( c ′ , d ′ ) ∈ Z Q n + 1 (c',d') \in \mathbb Z_Q^{n+1} (c′,d′)∈ZQn+1 中移除。现在 ( [ c ′ ′ ] q , [ d ′ ′ ] q ) ([c'']_q,[d'']_q) ([c′′]q,[d′′]q) 的相位是零。
- 将 ( c ′ ′ , d ′ ′ ) (c'',d'') (c′′,d′′) 缩放 q / α q/\alpha q/α,降低密文模数。

假定 PBS 输出的噪声界是 β \beta β,初始输入 ( c , d ) c,d) c,d) 的噪声上界也是 β \beta β,
- HomFloor:
- 输入噪声范围 ( − β , β ) (-\beta,\beta) (−β,β),执行 step 2 噪声范围 ( 0 , 2 β ) (0,2\beta) (0,2β),
- 执行 step 4,5,噪声范围是 ( 0 , 4 β ) (0,4\beta) (0,4β),这里需要 α ≥ 4 β \alpha \ge 4 \beta α≥4β,使得这个噪声不会影响到我们刚刚消除掉的 MSB,从而此时的 ( c , d ) (c,d) (c,d) 相位是 m ~ q + x \tilde mq+x m~q+x,其中 x ∈ [ 0 , q / 2 ) x \in [0,q/2) x∈[0,q/2) 包含了 LSD 以及噪声
- 执行 step 6 和 step 7,获得相位 x + e x+e x+e 的密文,从 ( c , d ) (c,d) (c,d) 中减掉后,返回的相位是 m ~ q + e \tilde mq+e m~q+e(注意函数 f 1 : x ∈ Z q / 2 ↦ x ∈ Z q / 2 f_1:x\in \mathbb Z_{q/2} \mapsto x \in \mathbb Z_{q/2} f1:x∈Zq/2↦x∈Zq/2,整个 x x x 都被清零,包括本来的噪声),满足 ∣ e ∣ < β |e| < \beta ∣e∣<β
- HomSign:
- 输入噪声范围 ( − β , β ) (-\beta,\beta) (−β,β),执行 HomFloor 输出的噪声范围也是 ( − β , β ) (-\beta,\beta) (−β,β),
- 执行 step 13 的模切换,噪声规模是 α / q ⋅ β + ( ∥ s ∥ 1 + 1 ) / 2 \alpha/q \cdot \beta + (\|s\|_1+1)/2 α/q⋅β+(∥s∥1+1)/2,
- 假如满足 ∥ s ∥ 1 = O ( n ) ≤ β \|s\|_1=O(n)\le \beta ∥s∥1=O(n)≤β,并且假设 q ≥ 4 α q\ge4\alpha q≥4α 以及 β ≥ 2 \beta\ge 2 β≥2,那么就有 α / q ⋅ β + ( ∥ s ∥ 1 + 1 ) / 2 < β \alpha/q \cdot \beta + (\|s\|_1+1)/2 < \beta α/q⋅β+(∥s∥1+1)/2<β,因此可以正确地执行 HomFloor
- 执行 step 17 虽然噪声规模可能超过 α \alpha α,但是并不会影响 MSB 的值,因此可以正确地执行 Boot,最终的噪声范围是 ( − β , β ) (-\beta,\beta) (−β,β)
当然,上述的分析是最坏情况的。如果使用平均情况,那么 ∥ s ∥ 2 = O ( n ) \|s\|_2 = O(\sqrt{n}) ∥s∥2=O(n),独立密文的加和噪声界 2 β \sqrt{2}\beta 2β,可以将 β \beta β 和 α \alpha α 都降低一些。
Using 3 PBS
为了给出通用的算法(尤其是 CKKS 的噪声和明文混合在一起),[LMP22] 给出了第二个方法:使用三次 PBS,支持任意的噪声, α ≥ 2 β \alpha \ge 2\beta α≥2β
基本思路:
- 首先消除 ( [ c ] q , [ d ] q ) ([c]_q,[d]_q) ([c]q,[d]q) 相位的第二高比特。现在(正的)噪声向上传播时,遇到被清零的第二高比特后,不再继续向 MSB 传递影响。
- 利用上一小节的算法,清理掉 LSD,然后模切换。

假定 PBS 输出的噪声界是 β \beta β,初始输入 ( c , d ) c,d) c,d) 的噪声上界也是 β \beta β,
- HomFloorAlt:
- 输入噪声范围 ( − β , β ) (-\beta,\beta) (−β,β),相位是 m ~ q + b q / 4 + x \tilde mq+bq/4+x m~q+bq/4+x,其中 b ∈ { 0 , 1 , 2 , 3 } , x ∈ [ 0 , q / 4 ) b \in \{0,1,2,3\},x \in [0,q/4) b∈{0,1,2,3},x∈[0,q/4),这里的 x x x 包含了噪声项
- 执行 step 3,4 将 LSD 的第二高比特置为零,相位形如 m ~ q + b ~ q / 2 + x + e \tilde mq+\tilde bq/2+x+e m~q+b~q/2+x+e,其中 b ~ ∈ { 0 , 1 } \tilde b \in \{0,1\} b~∈{0,1},噪声为 e ∈ [ 0 , 2 β ) e \in [0,2\beta) e∈[0,2β)
- 假设满足 q ≥ 8 β q \ge 8\beta q≥8β,那么 x + e < q / 4 + 2 β ≤ q / 2 x+e<q/4+2\beta\le q/2 x+e<q/4+2β≤q/2,它们不会改变 b b b 的值,因此并不会继续向更高的 m ~ \tilde m m~ 传播影响
- 执行 step 6,7 清理掉 b b b 的值,现在的相位是 m ~ q + x + e + e ′ \tilde mq+x+e+e' m~q+x+e+e′,它的 LSD 是 x + e + e ′ x+e+e' x+e+e′,其中 e ′ ∈ [ 0 , 2 β ) e' \in [0,2\beta) e′∈[0,2β)
- 进一步假设 q ≥ 16 β q \ge 16\beta q≥16β,那么满足 x + e + e ′ < q / 4 + 4 β ≤ q / 2 x+e+e' < q/4+4\beta \le q/2 x+e+e′<q/4+4β≤q/2,它落在了半环内
- 执行 step 9 清理掉它们,新的噪声是 e ′ ′ ∈ ( − β , β ) e'' \in (-\beta,\beta) e′′∈(−β,β)
- HomSign:
- 简单使用 HomFloorAlt 作为子例程,分析是一样的
PBS of Arbitrary Function
利用上述 HomFloor 的计算思路,为了利用 PBS 计算任意函数,我们可以将 m ∈ Z q / α m\in \mathbb Z_{q/\alpha} m∈Zq/α 扩展到 b ∥ m ∈ { m , m + q / α } ⊆ Z 2 q / α b\|m\in\{m,m+q/\alpha\} \subseteq \mathbb Z_{2q/\alpha} b∥m∈{m,m+q/α}⊆Z2q/α(随机的 b ∈ { 0 , 1 } b\in \{0,1\} b∈{0,1}),然后提取 sign 消除为 ( 0 ∥ m ) 2 = m (0\|m)_2=m (0∥m)2=m,接着使用半环上的函数执行 PBS 即可。
现在我们假定输入的 LWE 密文模数是 q q q,满足 2 q ∣ 2 N 2q \mid 2N 2q∣2N 可以被原始 PBS 支持。这导致相较于 HomFloor 中的 PBS,这里的 q q q 更小,明文精度丢失了 1 1 1 比特。

Homomorphic Digit Decomposition
为了执行 [GBA21] 的 Tree-based PBS(包括高精度 LWE 密文的自举),我们需要同态数字分解算法。因为 HomFloor 事实上就是在计算各个 Digit,并将它们从高精度 LWE 密文中减去的过程,因此仅需追踪此过程中产生的 ( [ c ] q , [ d ] q ) ([c]_q,[d]_q) ([c]q,[d]q) 即可。

输入 LWE 密文的相位 α ⋅ m + e \alpha \cdot m+e α⋅m+e,输出 k = log ( Q / α ) / log ( q / α ) k=\log(Q/\alpha)/\log(q/\alpha) k=log(Q/α)/log(q/α) 个密文,它们的相位是 α ⋅ m i + e i \alpha \cdot m_i+e_i α⋅mi+ei,满足 m = ∑ i = 0 k − 1 m i ⋅ ( q / α ) i m=\sum_{i=0}^{k-1} m_i \cdot (q/\alpha)^i m=∑i=0k−1mi⋅(q/α)i
Parameter Selection
略。。。
相关文章:

Large-Precision Sign using PBS
参考文献: [CLOT21] Chillotti I, Ligier D, Orfila J B, et al. Improved programmable bootstrapping with larger precision and efficient arithmetic circuits for TFHE[C]//Advances in Cryptology–ASIACRYPT 2021: 27th International Conference on the T…...

【电商项目实战】MD5登录加密及JSR303自定义注解
🎉🎉欢迎来到我的CSDN主页!🎉🎉 🏅我是Java方文山,一个在CSDN分享笔记的博主。📚📚 🌟推荐给大家我的专栏《电商项目实战》。🎯🎯 &am…...

2014,TEVC,A competitive swarm optimizer for large scale optimization(CSO)
PSO 分析(从而引入 CSO) CSO (competitive swarm optimizer) 算法是在PSO (particle swarm optimization) 算法的基础上改进而来的。PSO算法是一种功能强大、应用广泛的群体智能算法,主要用来解决优化问题。PSO算法包含一个粒子群࿰…...

【机器学习】【线性回归】梯度下降
文章目录 [toc]数据集实际值估计值估计误差代价函数学习率参数更新Python实现导包数据预处理迭代过程数据可视化完整代码 线性拟合结果代价结果 个人主页:丷从心 系列专栏:机器学习 数据集 ( x ( i ) , y ( i ) ) , i 1 , 2 , ⋯ , m \left(x^{(i)} , …...
JMeter逻辑控制器之While控制器
JMeter逻辑控制器之While控制器 1. 背景2.目的3. 介绍4.While示例4.1 添加While控制器4.2 While控制器面板4.3 While控制器添加请求4.3 While控制器应用场景 1. 背景 存在一些使用场景,比如:某个请求必须等待上一个请求正确响应后才能开始执行。或者&…...

记录 Docker 外部访问的基本操作
目录 1. 启动 docker 时挂载本地目录2. 外部访问 docker 容器 (-p/-P)3. 无法连接 docker 内 SSH 解决方案 1. 启动 docker 时挂载本地目录 # 将本地 D:/SDK 目录 挂载到 容器里的 /mnt/host 目录中 # 注意:-v /d/SDK:/mnt/host/ 必须放到 IMAGE_ID 前面才行 # …...
:BannerMessagePreference)
【Android 13】使用Android Studio调试系统应用之Settings移植(六):BannerMessagePreference
文章目录 一、篇头二、系列文章2.1 Android 13 系列文章2.2 Android 9 系列文章2.3 Android 11 系列文章三、BannerMessagePreference的移植3.1 新的问题:找不到 R.dimen.settingslib_preferred_minimum_touch_target3.2 问题分析(一)3.2.1 资源定义的位置3.2.2 检查依赖3.2…...

Python 变量
打印输出内容 print(‘rumenle’) print(‘haode’) 缩进需要tab 注释将需要注释的部分开头用# 多行注释 1、用你也可以左键选中我们需要注释的代码,松开,按:Ctrl/,就完成相同效果注释 2、把要注释的内容放到三个引号对里面 …...

ComfyUI如何中文汉化
comfyui中文地址如下: https://github.com/AIGODLIKE/AIGODLIKE-ComfyUI-Translationhttps://github.com/AIGODLIKE/AIGODLIKE-ComfyUI-Translation如何安装? 1. git安装 进入项目目录下的custom_nodes目录下,然后进入控制台,运…...
Glary Utilities Pro - 电脑系统优化全面指南:详尽使用教程
软件简介: Glary Utilities Pro 是一款全面的电脑优化工具,它旨在帮助用户提升计算机的性能和稳定性。这款软件提供了多种功能,包括系统清理、优化、修复以及保护。通过一键扫描,它可以识别并清除无用文件、临时数据、注册表错误等…...

1.4分页和排序
排序: -- 分页(limit)和排序(order by) -- 排序:升序ASC,降序DESC -- ORDER BY 通过字段排序,怎么排 -- 查询的结果根据成绩降序,升序 SELECT s.studentno,studentname,sub.subjectname,studentresult FROM student s RIGHT JO…...

Modbus转Profinet,不会编程也能用!轻松快上手!
Modbus转Profinet是一种用于工业自动化领域的通信协议转换器,可以将Modbus协议转换为Profinet协议,实现设备之间的数据交换与通信。这个工具的使用非常简单,即使没有编程经验的人也可以轻松上手。即使不会编程的人也可以轻松快速上手使用Modb…...
鸿蒙原生应用/元服务开发-Stage模型能力接口(十)下
ohos.app.form.FormExtensionAbility (FormExtensionAbility) 系统能力:SystemCapability.Ability.Form 示例 import FormExtensionAbility from ohos.app.form.FormExtensionAbility; import formBindingData from ohos.app.form.formBindingData; import formP…...

QT QPluginloader 加载失败,出现Unknown error 0x000000c1的问题
最近在学习Qt的插件开发,在加载插件时,一直失败,用如下代码加载并打印错误信息。 QDir dir("./testplugin.dll"); QPluginLoader pluginLoader(dir.absolutePath());//需要绝对路径 pluginLoader.load(); qDebug()<< "…...

众和策略:今年首次!A股罕见一幕
岁末,A股走出了不常见的行情。 这儿指的不单单是指数上涨。今天上午,A股逾3900只个股上涨,昨日逾4400只个股上涨,前天逾3700只个股上涨。据通达信数据显现,这种连续的普涨行情在本年还是头一次。 本年10月底…...
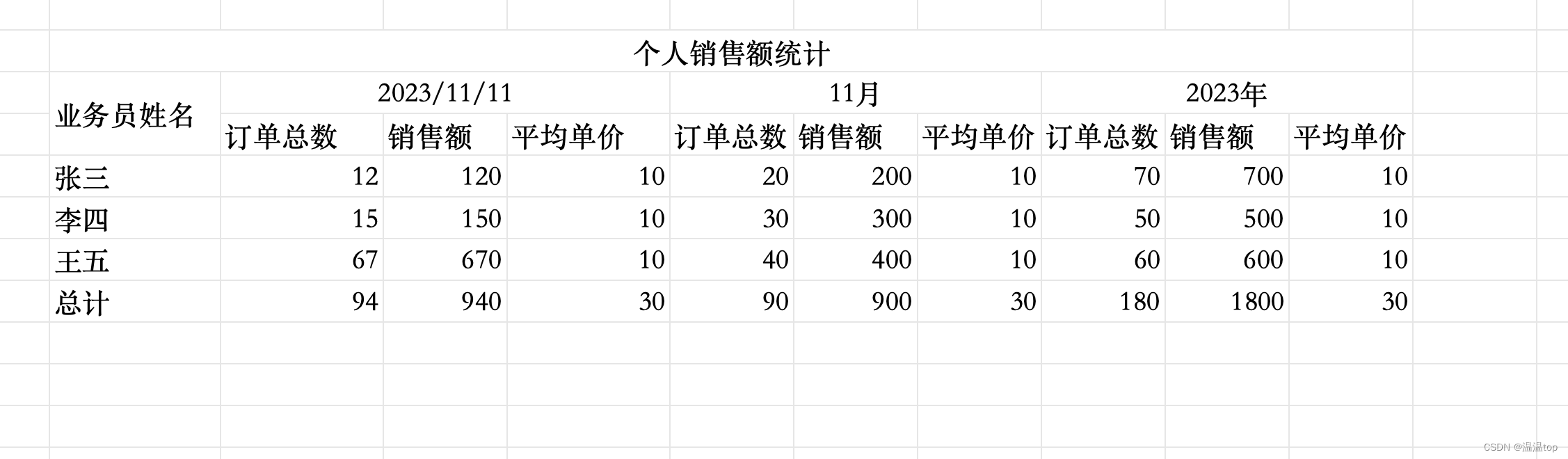
EasyExcel实现动态表头(注解实现)
要实现上述动态头,按每日统计,每月统计,每年统计。而时间是一直变化,所以我们需要表头也一直动态生成。 首先,我们需要定义所需要实体类 public class CountDayData {ExcelProperty(value "业务员姓名")p…...

什么是工厂方法模式,工厂方法模式解决了什么问题?
工厂方法模式是一种创建型设计模式,它定义了一个用于创建对象的接口,但将实际的实例化过程延迟到子类中。这样,客户端代码在不同的子类中实例化具体对象,而不是直接实例化具体类。工厂方法模式允许一个类的实例化延迟到其子类&…...
Flink 输出至 Elasticsearch
【1】引入pom.xml依赖 <dependency><groupId>org.apache.flink</groupId><artifactId>flink-connector-elasticsearch6_2.12</artifactId><version>1.10.0</version> </dependency>【2】ES6 Scala代码,自动导入的…...
web三层架构
目录 1.什么是三层架构 2.运用三层架构的目的 2.1规范代码 2.2解耦 2.3代码的复用和劳动成本的减少 3.各个层次的任务 3.1web层(表现层) 3.2service 层(业务逻辑层) 3.3dao 持久层(数据访问层) 4.结合mybatis简单实例演示 1.什么是三层架构 三层架构就是把…...

智能优化算法应用:基于厨师算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于厨师算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于厨师算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.厨师算法4.实验参数设定5.算法结果6.参考文献7.MA…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...
