【机器学习前置知识】Beta分布
Beta分布与二项分布的关系
Beta分布与二项分布密切相关,由二项分布扩展而来,它是用来描述一个连续型随机变量出现的概率的概率密度分布,表示为 X X X~ B e t a ( a , b ) Beta(a,b) Beta(a,b) , a 、 b a、b a、b 是形状参数。Beta分布本质上也是一个概率密度函数,只是这个函数的自变量和因变量都表示某种概率。
下面我们会先温故下二项分布的知识,然后循序渐进地引出Beta分布。
在二项分布这篇文章里介绍过,二项分布能解决的是 n次独立伯努利试验中成功k次的概率 问题,记作 X X X~ B i n ( n , p ) Bin(n,p) Bin(n,p) 。
仍以抛硬币为例,二项分布求的是抛 n n n 次硬币中出现 k k k 次正面向上的概率,它是一个概率质量函数(对离散型随机变量叫概率质量函数、对连续性随机变量叫概率密度函数),这个函数的自变量是 k k k ,因变量是概率,前提是硬币出现正面向上的概率 p p p (质地均匀)和抛的次数 n n n 是已知的。
假设一枚硬币质地均匀,也就是说抛一次硬币,出现正面向上和反面向上的概率 p p p 都为0.5,然后抛10次,下图是正面向上出现0次到10次的概率图:

附绘图代码
import numpy as np import matplotlib.pyplot as plt from scipy.stats import binom #plt.rcParams['font.family']=['Arial Unicode MS']n = 10 #试验次数 p = 0.5 #正面向上的概率#生成x轴的数据点 x = np.arange(0, n + 1, 0.001)#二项分布的概率质量函数(PMF)和累积分布函数(CDF) pmf = binom.pmf(x, n, p) #cdf = binom.cdf(x, n, p)plt.figure(figsize=(10, 5)) plt.subplot(121) plt.plot(x, pmf, 'b-', lw=2, label='PMF') plt.vlines(x, 0, pmf, colors='b', lw=1, alpha=0.5) plt.xlabel('正面向上次数') plt.ylabel('概率') plt.title('二项分布-抛硬币10次') plt.legend() plt.show()
正常来说,我们可以提前就预料到结果中出现5次正面向上的概率最大,实际上也雀食如此。但这是对质地均匀的硬币来说的,如果是一枚质地不均匀的硬币,我们还能这么信誓旦旦地判断吗?
再假设我们拿到了一枚不知道是否质地均匀的硬币,然后想求抛一次硬币正面向上的概率。这个问题如何解决呢?
一个粗糙的解决方案是: 我尽可能地多抛硬币,然后看所有结果中正面向上出现的概率是多少,这个概率就是抛一次硬币正面向上的概率的逼近。比如我茶不思饭不想地连续抛了10000次硬币,其中出现正面向上的有3000次,现在我可以自信地说再抛一次硬币正面向上的概率 大概 就是0.3。注意我这里用了大概两个字,也就是说0.3这个概率只是抛一次硬币中正面向上出现的所有概率中最大的一个概率,那有没有可能是0.4、0.5甚至0.9呢?是有可能的,只是这些概率出现的概率都相对0.3 更低 罢了。
再试想一下,我只抛了100次,其中出现正面向上的有30次,那我判断再抛一次硬币正面向上的概率是0.3的 把握 是不是会比10000次出现3000次 更低 呢?
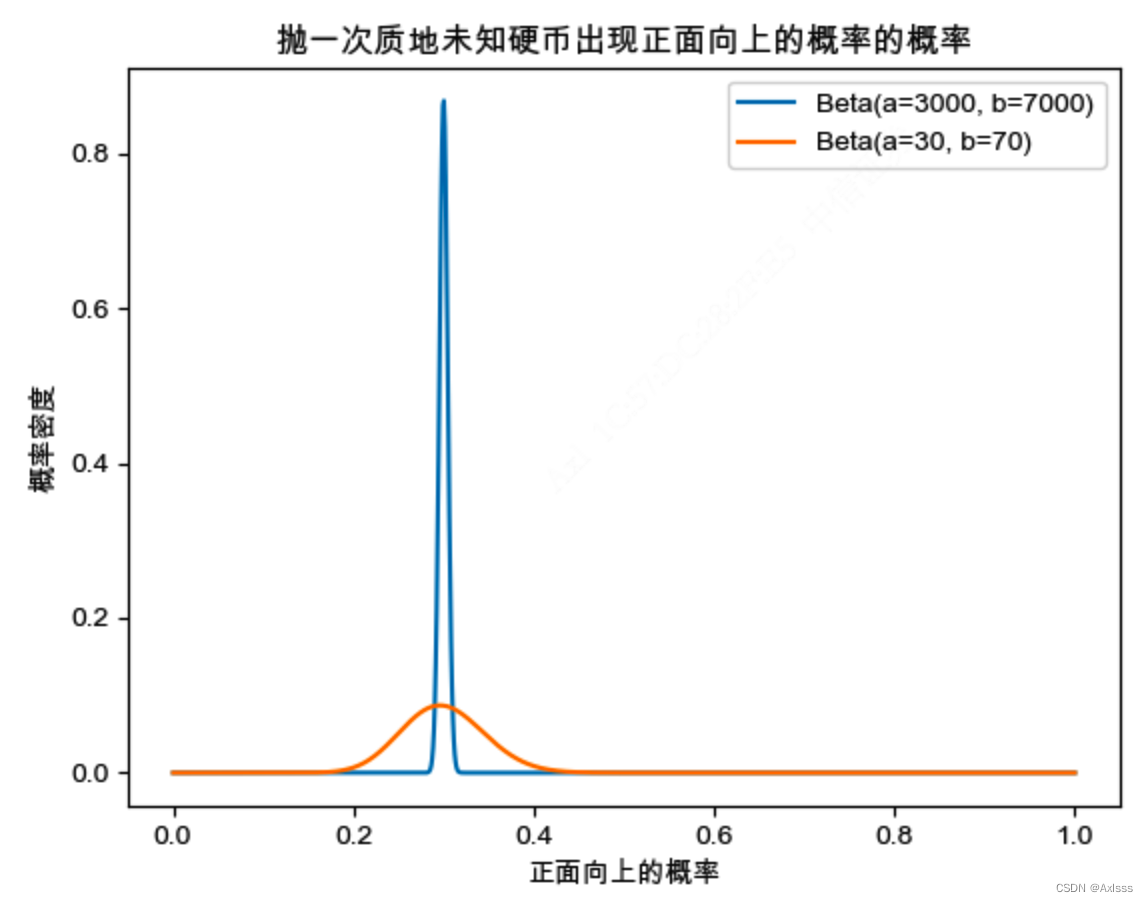
用图展示一下抛一次质地未知硬币出现正面向上的概率的概率(先验知识是已知抛了n次中出现正面向上的有a次):
附绘图代码
import numpy as np import matplotlib.pyplot as plt from scipy.stats import beta #plt.rcParams['font.family']=['Arial Unicode MS']a1 = 3000 # 抛一万次硬币中正面向上的次数 b1 = 7000 # 抛一万次硬币中反面向上的次数 a2 = 30 # 抛一百次硬币中正面向上的次数 b2 = 70 # 抛一百次硬币中反面向上的次数x = np.linspace(0.0, 1.0, 1000)# 计算Beta分布的概率密度函数值 y1 = beta.pdf(x, a1, b1) y2 = beta.pdf(x, a2, b2)plt.plot(x, y1, label='Beta(a={}, b={})'.format(a1, b1)) plt.plot(x, y2, label='Beta(a={}, b={})'.format(a2, b2)) plt.xlabel('正面向上的概率') plt.ylabel('概率密度') plt.title('抛一次质地未知硬币出现正面向上的概率的概率') plt.legend() plt.show()
这个图像表示了抛一次质地未知硬币出现正面向上的概率的概率分布,其中图像的形状随参数a和b的不同而变化。从图中可以看出:
- 基于抛10000次硬币中出现正面向上3000次的是蓝色曲线,其在横坐标上正面向上的概率为0.3处取得最大值,即再抛一次硬币出现正面向上的概率是0.3的结果最为确信;
- 基于抛100次硬币中出现正面向上30次的是橙色曲线,其也在横坐标上正面向上的概率为0.3处取得最大值,即再抛一次硬币出现正面向上的概率是0.3的结果最为确信,但与蓝色曲线对比可以看出,明显橙色曲线对此判断的把握要比蓝色曲线小得多;
那么如何去量化上面提到的 更低 与 把握 ?此时就该Beta分布登场了!
细心的小伙伴可以看出上图就是用Beta函数画出来的图像。
文章开头说过Beta分布的表示为 X X X~ B e t a ( a , b ) Beta(a,b) Beta(a,b) ,其中 a 、 b a、b a、b 是形状参数,可以控制图像的形状。对应到抛硬币场景中,
相关文章:

【机器学习前置知识】Beta分布
Beta分布与二项分布的关系 Beta分布与二项分布密切相关,由二项分布扩展而来,它是用来描述一个连续型随机变量出现的概率的概率密度分布,表示为 X X X~ B e t a ( a , b ) Beta(a,b) Beta(a,b) , a 、 b a、b a、b 是形状参数。Beta分布本质上也是一个概率密度函数,只是这…...

Notepad++批量更改文件编码格式及文档格式
背景: 在项目中遇到Windows平台VS的MSVC编译不识别Unix下UTF-8编码导致的编译失败问题。需要将Unix下的UTF-8转为UTF-8-BOM格式。网上找了些方式,之后又深入探究了下文档转换的可能性,共享给大家。(当然Windows和Unix平台代码格式…...
Linux驱动开发学习笔记6《蜂鸣器实验》
目录 一、蜂鸣器驱动原理 二、硬件原理分析 三、实验程序编写 1、 修改设备树文件 (1)添加pinctrl节点 (2)添加BEEP设备节点 (3)检查PIN 是否被其他外设使用 2、蜂鸣器驱动程序编写 3、编写测试AP…...
鸿蒙(HarmonyOS 3.1) DevEco Studio 3.1开发环境汉化
鸿蒙(HarmonyOS 3.1) DevEco Studio 3.1开发环境汉化 一、安装环境 操作系统: Windows 10 专业版 IDE:DevEco Studio 3.1 SDK:HarmonyOS 3.1 二、设置过程 打开IDE,在第一个菜单File 中找到Settings...菜单 在Setting...中找到Plugins…...
毫米波雷达:从 3D 走向 4D
1 毫米波雷达已广泛应用于汽车 ADAS 系统 汽车智能驾驶需要感知层、决策层、执行层三大核心系统的高效配合,其中感知层通过传感器探知周围的环境。汽车智能驾驶感知层将真实世界的视觉、物理、事件等信息转变成数字信号,为车辆了解周边环境、制定驾驶操…...

CENTOS docker拉取私服镜像
概述 docker的应用越来越多,安装部署越来越方便,批量自动化的镜像生成和发布都需要docker镜像的拉取。 centos6版本太老,docker的使用过程中问题较多,centos7相对简单容易。 本文档主要介绍centos系统安装docker和拉取docker私…...

【前端面经】即时设计
目录 前言一面git 常见命令跨窗口通信vue 响应式原理发布订阅模式翻转二叉树Promise.all()扁平化数组面试官建议 二面Event Loop 原理Promise 相关css 描边方式requestAnimationReact 18 新特性JSX 相关react 输出两次函数式编程React 批处理机制http请求头有哪些本地存储性能优…...
前端三件套html/css/js的基本认识以及示例程序
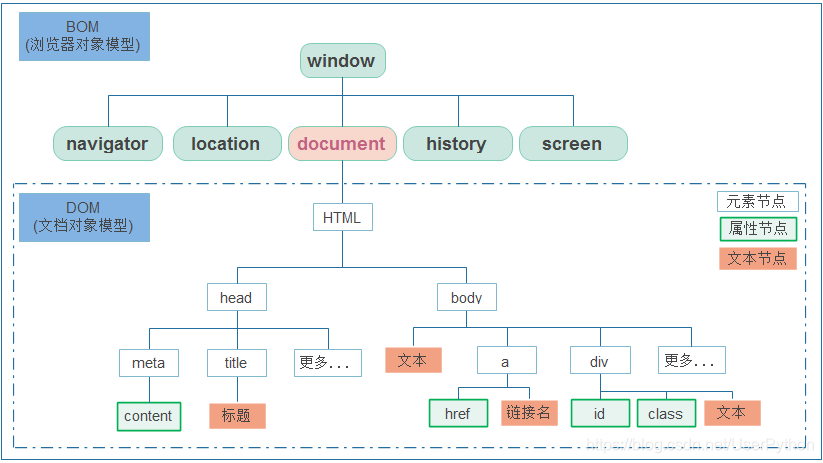
简介 本文简要讲解了html,css,js.主要是让大家简要了解网络知识 因为实际开发中很少直接写html&css,所以不必过多纠结,了解一下架构就好 希望深度学习可以参考MDN和w3school HTML 基础 HTML (Hyper Text Markup Language) 不是一门编程语言,而是一种用来告知浏览器如…...
云计算:OpenStack 配置云主机实例的存储挂载并实现外网互通
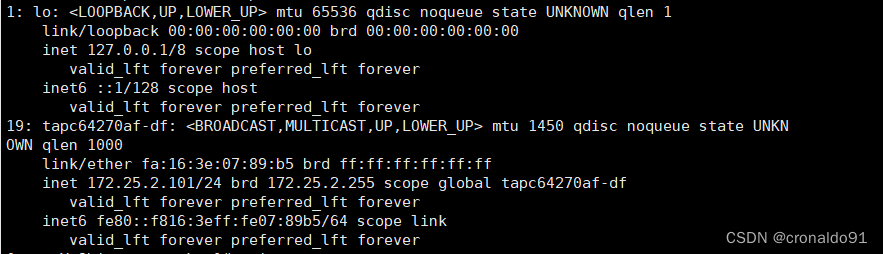
目录 一、实验 1. 环境 2.配置存储挂载 3.云主机实例连接外部网络(SNAT) 4.外部网络连接云主机实例(DNAT) 二、问题 1.云主机 ping 不通外部网络 2.nova list 查看云主机列表报错 3.nova list 与 virsh list --all有何区…...
python/selenium/jenkins整合
1、新建python项目,专门写selenium代码,建议用pytest框架写。 2、把代码上传到代码库中。 3、环境配置: 3.1 在跑jenkins的机器上配置好python环境,需要python --version能在任何地方运行(配置好系统环境变量&#…...

华为路由器ACL操作SSH接口
ACL的定义 访问控制列表(Access Control Lists,ACL)是应用在路由器接口的指令列表。这些指令列表用来告诉路由器哪些数据包可以收、哪些数据包需要拒绝。至于数据包是被接收还是拒绝,可以由类似于源地址、目的地址、端口号等的特…...

Flutter 三点三:Dart Stream
Stream Stream用于接收异步事件Stream 可以接收多个异步事件Stream.listen()方法返回StreamSubscription 可用于取消事件订阅,取消后,不再接收事件 基本使用 Stream.fromFutures([Future.delayed(Duration(seconds: 1),(){return "事件1";})…...

centos 防火墙 设置 LTS
centos 防火墙 设置 LTS https://blog.csdn.net/m0_58805648/article/details/130671008...
SAP缓存 表缓存( Table Buffering)
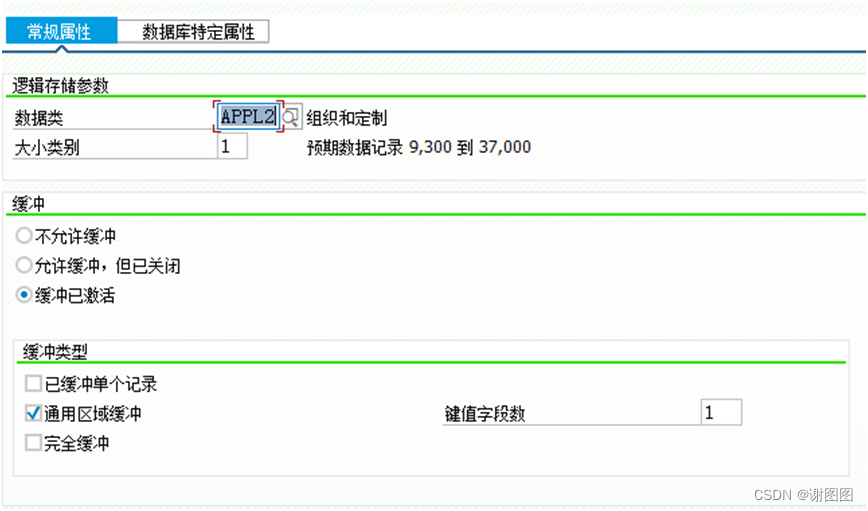
本文主要介绍SAP中的表缓存在查询数据,更新数据时的工作情况以及对应概念。 SAP表缓存的工作 查询数据 更新数据 删除数据 表缓存的概念 表缓存技术设置属性 不允许缓冲: 允许缓冲,但已关闭: 缓冲已激活: 已…...

Mybatis插件入门
专栏精选 引入Mybatis Mybatis的快速入门 Mybatis的增删改查扩展功能说明 mapper映射的参数和结果 Mybatis复杂类型的结果映射 Mybatis基于注解的结果映射 Mybatis枚举类型处理和类型处理器 再谈动态SQL Mybatis配置入门 Mybatis行为配置之Ⅰ—缓存 Mybatis行为配置…...
DOA估计算法——迭代自适应算法(IAA)
1 简介 迭代自适应法 (Iterative Adaptive Approach,IAA)估计算法最早由美国的电气工程师和数学家Robert Schmidt和Roy A. Kuc在1986年的一篇论文"Multiple Emitter Location and Signal Parameter Estimation"中首次提出了这一算法, IAA DOA …...
Python If语句以及代码块的基本介绍
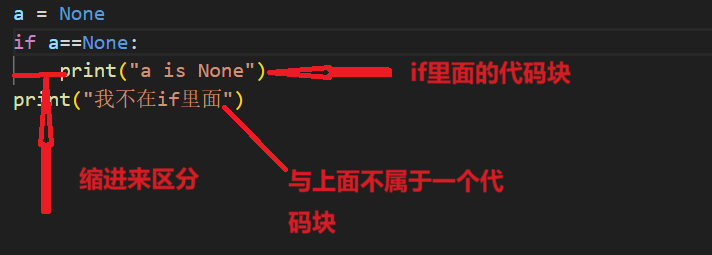
if语句 在编程中if语句是一种根据条件执行不同代码块的控制结构,他根据条件的真假来分支程序的执行路径,所以我们可以通过if语句根据不同情况而执行不同的程序 格式 if [条件(bool值或者计算结果为bool类型的算式)] : a11if a>10:print("a大于10") # --> a大…...
[嵌入式专栏](FOC - SVPWM扇区计算Part1)
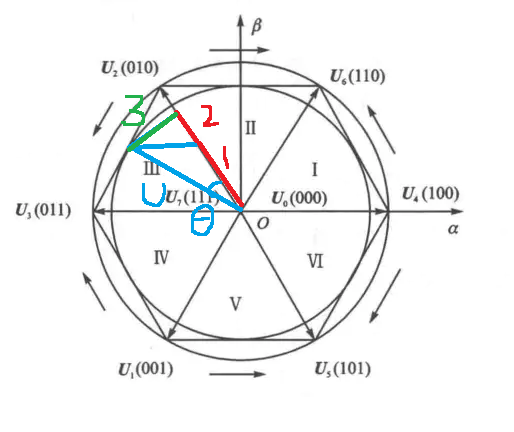
文章目录 1 . 概要2 . 扇区计算2.1 扇区Ⅰ计算2.2 扇区Ⅱ计算2.3 扇区Ⅲ计算 3 . 小结 【极客技术传送门】 : https://blog.csdn.net/Engineer_LU/article/details/135149485 1 . 概要 经过扇区判断后,就知道在哪个扇区进行输出了 【Q】但是每个扇区分别输出怎样的结…...

亚马逊美国站ASTM F2613儿童折叠椅和凳子强制性安全标准
ASTM F2613折叠椅和凳子安全标准 美国消费品安全委员会(CPSC)发布的ASTM F2613儿童折叠椅和凳子的强制性安全标准,已于2020年7月6日生效,并被纳入联邦法规《16 CFR 1232儿童折叠椅和凳子安全标准》。 亚马逊要求在美国站上架的儿…...
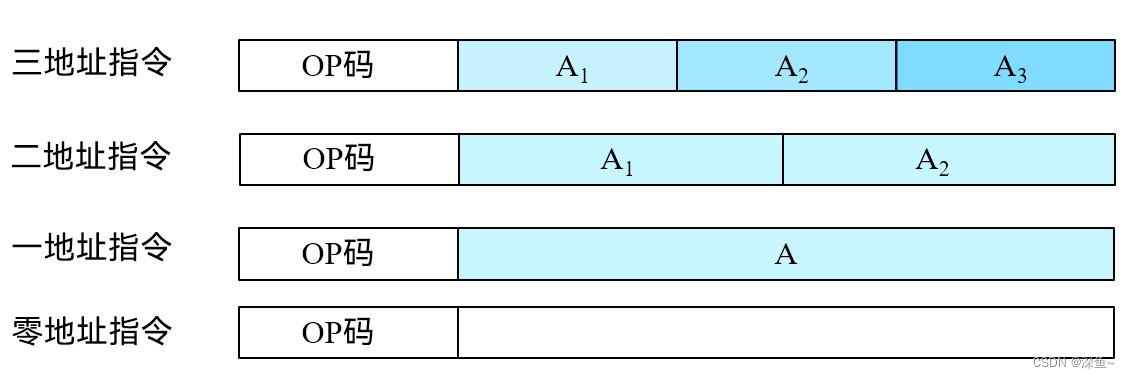
【机组期末速成】指令系统|机器指令概述|操作数类型与操作类型|寻址方式|指令格式
🎥 个人主页:深鱼~🔥收录专栏:计算机组成原理🌄欢迎 👍点赞✍评论⭐收藏 目录 前言: 一、本章考点总览 二、考点分析 1、以下有关指令系统的说法中错误的是( )。 2…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...
