【C/C++ 数据结构】-八大排序之 冒泡排序快速排序
作者:学Java的冬瓜
博客主页:☀冬瓜的主页🌙
专栏:【C/C++数据结构与算法】
分享:那我便像你一样,永远躲在水面之下,面具之后! ——《画江湖之不良人》
主要内容:八大排序选择排序中的冒泡排序、选择排序(递归+非递归),理解快速排序一趟排序的三种算法:挖坑法,左右指针法,前后指针法。还有关于快排优化:三数取中法,小区间优化。


文章目录
- 一、冒泡排序
- 1. 思路
- 2. 复杂度
- 3. 代码
- 二、快速排序
- 1. 思路:
- 方法:挖坑法、左右指针、前后指针
- 优化操作:三数取中法、小区间优化
- 2. 复杂度
- 3. 代码
- 3.1 挖坑法 左右指针 前后指针(一趟排序)
- 3.2 三数取中 小区间优化 递归实现排序
- 4. 补充:测试排序性能方法
- 5. 补充:快排非递归
一、冒泡排序
1. 思路
理解:这是排序中几乎最简单的一个排序。比如要把一组数从小到大排序,就是依次比较两数大小,大的数往后挪,直到最大数放在最后面这就完成了一次冒泡。然后最后边界减一,和之前一样的操作,直到完成n-1次冒泡。最重要的是:
注意边界下标的控制!
2. 复杂度
时间复杂度:
O(N^2)
如果使用优化版(使用一个变量标记在一趟排序中是否发生了交换,不发生交换,则表示这组数据刚好符合排序要求),且这组数刚好是按照要求,从小到大排的(和示例代码一致),那么时间复杂度达到O(N)
3. 代码
// 冒泡排序1(优化版)
// 时间复杂度:O(N^2)
void BubbleSort(int* arr, int size)
{for (int i = 0; i < size - 1; i++) {int exchange = 0;for (int j = 1; j < size - i; j++) {if (arr[j - 1] > arr[j]) {Swap(&arr[j - 1], &arr[j]);exchange = 1;}}if (exchange == 0) {break;}}
}
// 冒泡排序2
void BubbleSort(int* arr, int size)
{// 利用end控制末尾边界int end = size;while (end > 0) {for (int j = 1; j < end; j++) {if (arr[j - 1] > arr[j]) {Swap(&arr[j - 1], &arr[j]);}}end--;}
}
二、快速排序
1. 思路:
方法:挖坑法、左右指针、前后指针
- 挖坑法:随机或者选择开头第一个数做key,把右边比key小的数挪到左边,把左边比key大的数挪到右边,这样就找到了key的位置(即把key放入了该放的位置),然后左右在分
【left,key-1】 key 【key+1,right】的区间去递归找到并放入每一个数到排序中该放的数。 - 左右指针:begin下标从左找比key大的数,end下标从右找比key小的数,然后交换位置,直到begin遇到end,和挖坑法很相似。
- 前后指针:cur下标在前,prev下标紧跟其后从左到右搜索。cur下标找到比key小的数时,先prev++,然后 Swap(&a[prev],a[cur]) ;会有两种情况:其一:cur就在prev后一个,prev++后赋值,是自己给自己赋值。其二:cur和prev之间隔着大于key的数,交换就是把cur下标所在的这个比key小的数和prev与cur之间比key大的数交换。结局就是比key小的数放在了前面,大的数移到了后面。
优化操作:三数取中法、小区间优化
-
三数取中法对有序的有大量数据的数组很有作用,可以大大加大快速排序的效率。

-
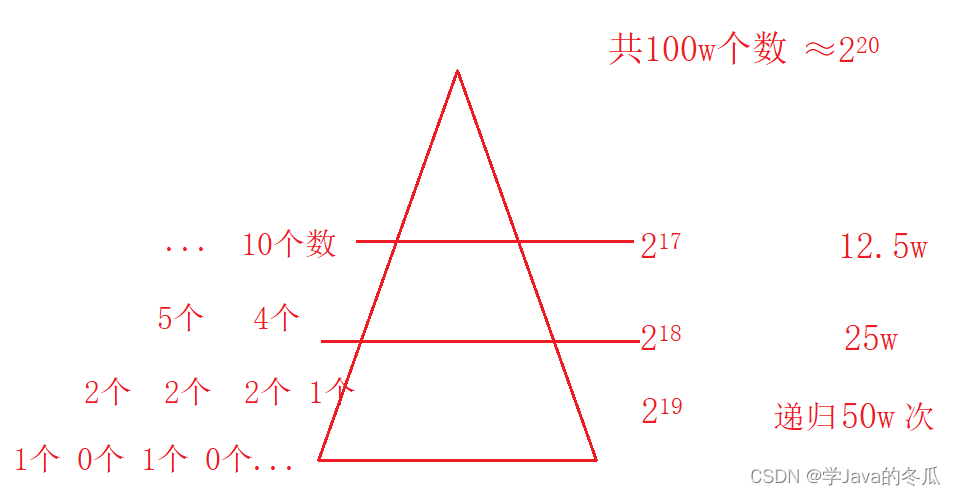
小区间优化目的是:减少函数递归,从而减少栈帧的创建和销毁,提高效率,但是一般不是很明显。比如对长度100w的数组排序,最后三层就占了87.5w次递归。
2. 复杂度
- 时间复杂度:
O(NlogN)。每次挖坑后区间减半,分两边去操作,一共需要排序N个数据,所以,需要选择key共logN次,每个数找它的位置时,要遍历整个数组(长度为N)。所以复杂度为O(NlogN)。
3. 代码
3.1 挖坑法 左右指针 前后指针(一趟排序)
// 一趟排序
// 法一:挖坑法
int FuncPart1(int* a, int left, int right)
{// 三数取中法int mid = getMidIndex(a + left, right - left + 1);Swap(&a[left], &a[left + mid]); // 注意范围理解int begin = left, end = right;int pivot = begin;int key = a[begin];// 1、排序一趟的操作while (begin < end){ // 2、右边找小while (begin < end && key <= a[end]) // 要加上begin<end的条件,如果从外面的while进入后,end--; // 内层的while不判断就操作,会导致begin和end错开,从而出现错误排序//Swap(&a[pivot], &a[end]); //注意:不能直接交换,不然交换时消耗大量时间就达不到快速的效果// 2.1、把坑位赋值为这个右边比key小的这个数,再更新坑位pivota[pivot] = a[end];pivot = end;// 3、左边找大while (begin < end && a[begin] <= key)begin++;//Swap(&a[begin], &a[pivot]); //注意:不能直接交换,不然交换时消耗大量时间就达不到快速的效果// 3.1、把坑位赋值为这个左边比key大的这个数,再更新坑位pivota[pivot] = a[begin];pivot = begin;}// 4、把key这个数放进它的位置pivot = begin;a[begin] = key;return pivot;
}// 法二:左右指针法
int FuncPart2(int* a, int left, int right)
{int mid = getMidIndex(a, right - left + 1);Swap(&a[left], &a[left + mid]);int begin = left;int end = right;int keyi = begin;while (begin < end) {// 找小while (begin < end && a[keyi] <= a[end]) {end--;}// 找大while (begin < end && a[begin] <= a[keyi]) {begin++;}Swap(&a[begin], &a[end]);}Swap(&a[begin], &a[keyi]);keyi = begin;return keyi;
}// 法三:前后指针法
int FuncPart3(int* a, int left, int right)
{int mid = getMidIndex(a, right - left + 1);Swap(&a[left], &a[left + mid]);int prev = left, cur = left + 1;int keyi = left;while (cur <= right) {if (a[cur] < a[keyi] && ++prev != cur) { // 注解:1只要cur的值小于keyi的值,prev就自增,即prev要标记左边最后比keyi小的数。Swap(&a[prev], &a[cur]); // 2当进入if时,prev刚好在cur的后一个时,就是cur自己赋值给自己。}++cur;}// 注意:退出循环时,prev下标的值是最后一个比keyi值小的数,所以交换二者后,keyi就找到它的位置。Swap(&a[keyi], &a[prev]);keyi = prev;return keyi;
}
3.2 三数取中 小区间优化 递归实现排序
// 三数取中
int getMidIndex(int* a, int n)
{int left = 0;int right = n - 1;int mid = (left + right) / 2;if (a[left] < a[mid]) {if (a[mid] < a[right]) {return mid;}//a[mid]>a[right]else if (a[left] < a[right]) { return right;} // a[left]<a[mid] a[mid]>a[right] a[left]>=a[right]else {return left;}}// a[left] >= a[mid]else {if (a[mid] > a[right]) {return mid;}// a[mid] < a[right]else if (a[right] > a[left]) {return left;}//a[left]>=a[mid] a[mid]<a[right] a[right]<=a[left]else {return right;}}
}void QuickSort(int* a, int left, int right)
{if (left >= right){return;}int pivot = FuncPart3(a, left, right); 注意0:在数据量在一定范围内,无序情况下快排比堆排和希尔都快,但有序时,快排要慢很多。// 分成区间[left,pivot-1] pivot [pivot+1,right],递归去实现子区间有序//QuickSort(a , left, pivot - 1);//QuickSort(a , pivot + 1, right);// 小区间优化(n<=10,使用直接插入排序,但是这个方法优化效率不明显)if (pivot - 1 - left > 10) {QuickSort(a, left, pivot - 1);}else {InsertSort(a + left, pivot - 1 - left + 1);}if (right - (pivot + 1) > 10) {QuickSort(a, pivot + 1, right);}else {InsertSort(a + pivot + 1, right - (pivot + 1) + 1);}
}
4. 补充:测试排序性能方法
// 测试性能
void TestOP()
{// 使用malloc申请新的空间,那么第二个排序就不会收到第一个排序结果的影响。否则,如果只使用传入的数组,排完一次后就有序了,那么其它排序前,数组就已经有序了。srand(time(NULL)); // 产生随机数int N = 1000000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a7 = (int*)malloc(sizeof(int) * N);int* a8 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand();//a1[i] = i;//a1[i] = N-i;a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];a8[i] = a1[i];}long int begin1 = clock(); // 获取毫秒数InsertSort(a1, N);long int end1 = clock();long int begin2 = clock();ShellSort(a2, N);long int end2 = clock();long int begin3 = clock();SelectSort(a3, N);long int end3 = clock();long int begin4 = clock();HeapSort(a4, N);long int end4 = clock();long int begin5 = clock();BubbleSort(a5, N);long int end5 = clock();long int begin6 = clock();QuickSort(a6, 0, N - 1);long int end6 = clock();long int begin7 = clock();MergeSort(a7, N);long int end7 = clock();printf("直接插入:%ld ms\n", end1 - begin1);printf("希尔排序:%ld ms\n", end2 - begin2);printf("选择排序:%ld ms\n", end3 - begin3);printf("堆排序 :%ld ms\n", end4 - begin4);printf("冒泡排序:%ld ms\n", end5 - begin5);printf("快速排序:%ld ms\n", end6 - begin6);printf("归并排序:%ld ms\n", end7 - begin7);
}
5. 补充:快排非递归
- 注意:对快排来说(不分递归非递归),逆序会比随机或者顺序慢很多,因为即使使用三数取中法,左右数字全都是需要交换的,复杂度虽然没有到O(N^2),但比O(NlogN)大很多。
- 快速排序有了非递归,为什么还要实现非递归呢?
非递归最根本的原因就是为了解决栈溢出的问题。排序的数据量很大时(比如1000w个数),递归的深度会很深,栈帧开销过大,这会让只有十几兆的栈空间不够用,导致栈溢出。 - 下面的例子是借用数据结构的栈,来模拟实现快排。要看栈可以看这篇博客:栈和队列。
- 另外,快排非递归也可以利用队列来实现,利用先进先出的规则。比如4 2 9 5 1 3 8,忽略三数取中法,利用栈或队列如下:

// 非递归:
// 快速排序:
int FuncPart(int* a, int left, int right)
{ 三数取中法int mid = getMidIndex(a + left, right - left + 1);Swap(&a[left], &a[left + mid]); // 注意理解范围int begin = left, end = right;int pivot = begin;int key = a[begin];// 1、排序一趟的操作while (begin < end){ // 2、右边找小while (begin < end && key <= a[end]) // 要加上begin<end的条件,如果从外面的while进入后,end--; // 内层的while不判断就操作,会导致begin和end错开,从而出现错误排序//Swap(&a[pivot], &a[end]); //注意:不能直接交换,不然交换时消耗大量时间就达不到快速的效果// 2.1、把坑位赋值为这个右边比key小的这个数,再更新坑位pivota[pivot] = a[end];pivot = end;// 3、左边找大while (begin < end && a[begin] <= key)begin++;//Swap(&a[begin], &a[pivot]); //注意:不能直接交换,不然交换时消耗大量时间就达不到快速的效果// 3.1、把坑位赋值为这个左边比key大的这个数,再更新坑位pivota[pivot] = a[begin];pivot = begin;}// 4、把key这个数放进它的位置pivot = begin;a[begin] = key;return pivot;
}
void QurickSortNonR(int* a, int n)
{Stack st;StackInit(&st);StackPush(&st, n - 1);StackPush(&st, 0);while (!StackEmpty(&st)) {int left = StackTop(&st);StackPop(&st);int right = StackTop(&st);StackPop(&st);int Index = FuncPart(a, left, right); // 用挖坑法,一趟排序// [left, index-1] index [index+1, right]// Push先入右,后入左,那Pop先出左if (Index + 1 < right) { // 代表Index右边至少还有两数没排,继续入栈StackPush(&st, right);StackPush(&st, Index + 1);}if (left < Index - 1) {StackPush(&st, Index - 1);StackPush(&st, left);}}
}
相关文章:

【C/C++ 数据结构】-八大排序之 冒泡排序快速排序
作者:学Java的冬瓜 博客主页:☀冬瓜的主页🌙 专栏:【C/C数据结构与算法】 分享:那我便像你一样,永远躲在水面之下,面具之后! ——《画江湖之不良人》 主要内容:八大排序选…...

苹果ipa软件下载网站和软件的汇总
随着时间的流逝,做苹果版软件安装包下载网站和软件的渐渐多了起来。 当然,已经关站、停运、下架、倒闭的苹果软件下载网站和软件我就不说了,也不必多说那些关站停运下架倒闭的网站和软件了。 下面我统计介绍的就是苹果软件安装包下载网站和软…...
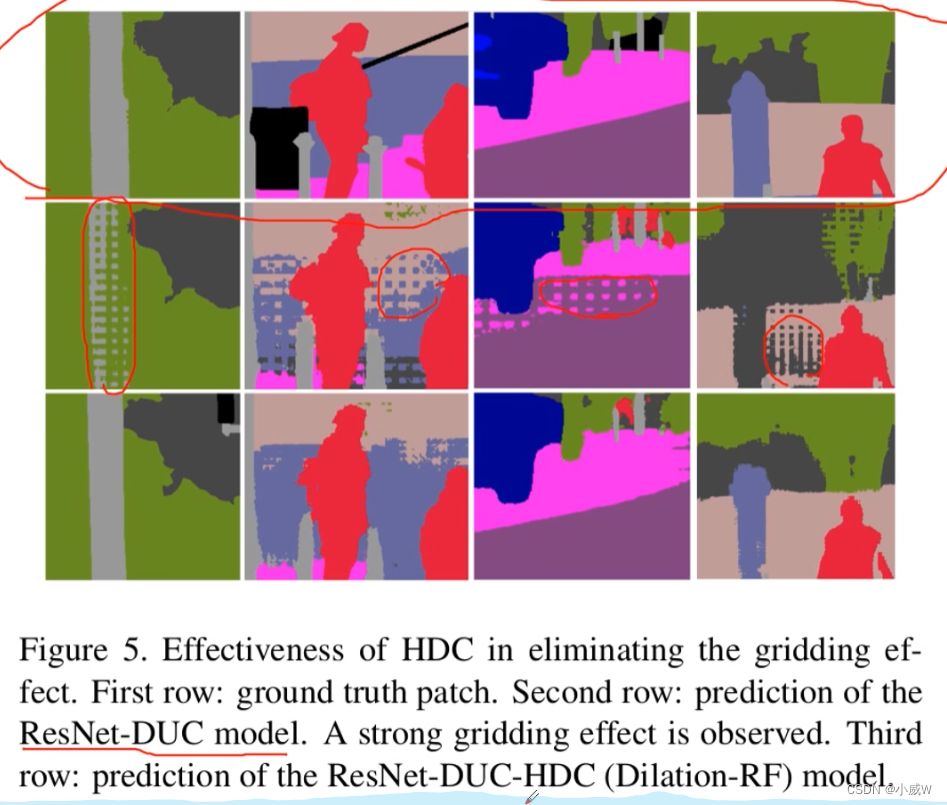
深度学习-【语义分割】学习笔记4 膨胀卷积(Dilated convolution)
文章目录膨胀卷积为什么需要膨胀卷积gridding effect连续使用三次膨胀卷积——1连续使用三次膨胀卷积——2连续使用三次膨胀卷积——3Understanding Convolution for Semantic Segmentation膨胀卷积 膨胀卷积,又叫空洞卷积。 左边是普通卷积,右边是膨胀…...

【10】SCI易中期刊推荐——工程技术-计算机:人工智能(中科院2区)
🚀🚀🚀NEW!!!SCI易中期刊推荐栏目来啦 ~ 📚🍀 SCI即《科学引文索引》(Science Citation Index, SCI),是1961年由美国科学信息研究所(Institute for Scientific Information, ISI)创办的文献检索工具,创始人是美国著名情报专家尤金加菲尔德(Eugene Garfield…...
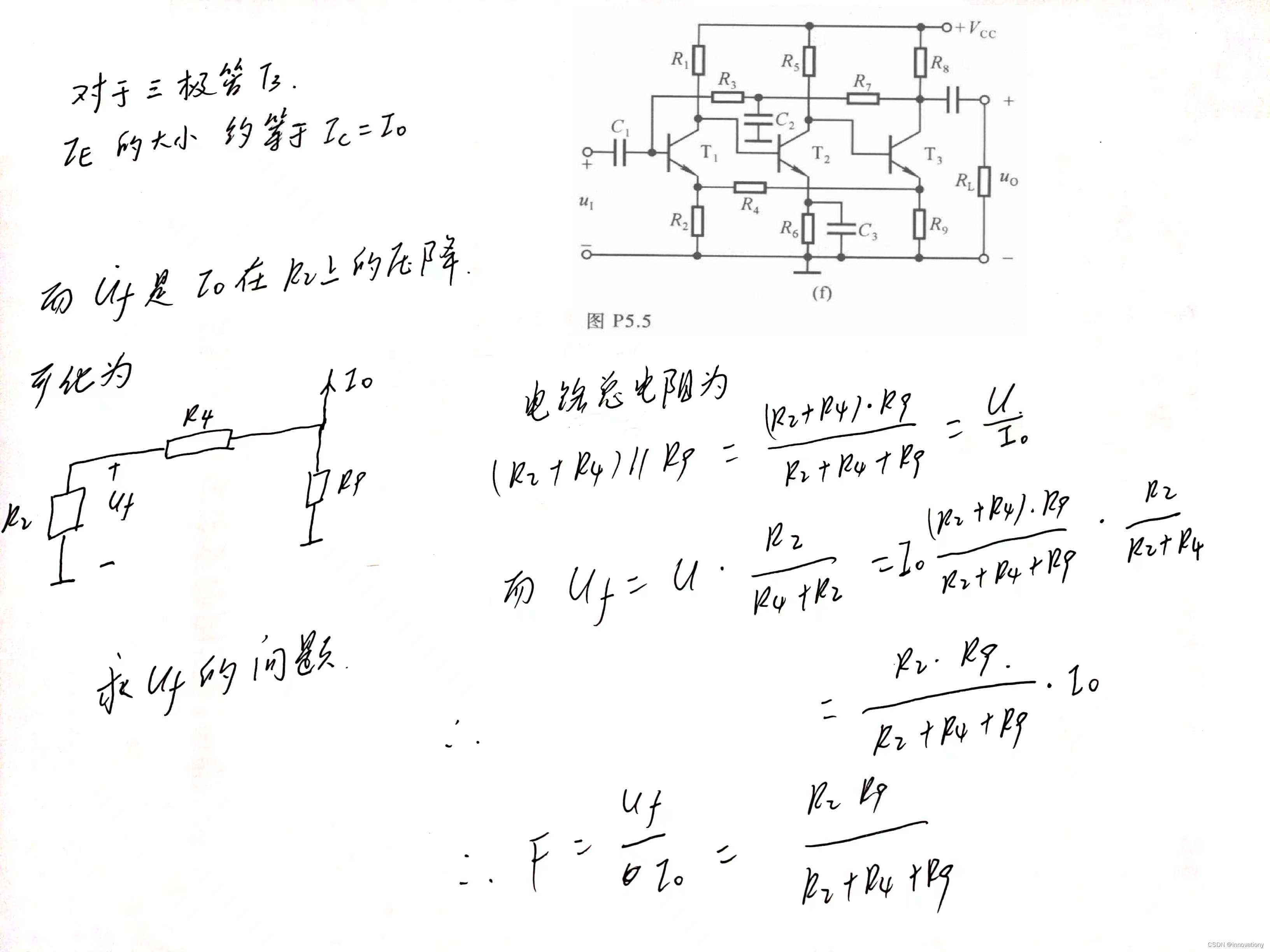
模电计算反馈系数,有时候转化为计算电阻分压的问题
模电计算反馈系数,有时候转化为计算电阻分压的问题 如果是电压反馈,F的除数是Uo 如果是电流反馈,F的除数是Io 串联反馈,F的分子是Uf 并联反馈,F的分子是If 点个赞呗,大家一起加油学习!...

专治Java底子差,不要再认为泛型就是一对尖括号了
文章目录一、泛型1.1 泛型概述1.2 集合泛型的使用1.2.1 未使用泛型1.2.2 使用泛型1.3 泛型类1.3.1 泛型类的使用1.2.2 泛型类的继承1.4 泛型方法1.5 泛型通配符1.5.1 通配符的使用1)参数列表带有泛型2)泛型通配符1.5.2 泛型上下边界1.6 泛型的擦除1.6.1 …...
PayPal轮询收款的那些事儿
想必做跨境电商独立站的小伙伴,对于PayPal是再熟悉不过了,PayPal是一个跨国际贸易的支付平台,对于做独立站的朋友来说跨境收款绝大部分都是依赖PayPal以及Stripe条纹了。简单来说PayPal跟国内的支付宝有点类似,但是PayPal它是跨国…...
【Linux】项目自动化构建工具——make/Makefile
目录 1.make与Makefile的关系 Makefile make 项目清理 clean .PHONY 当我们编写一个较大的软件项目时,通常需要将多个源文件编译成可执行程序或库文件。为了简化这个过程,我们可以使用 make 工具和 Makefile 文件。Makefile 文件可以帮助我们自动…...

成本降低90%,OpenAI正式开放ChαtGΡΤ
今天凌晨,OpenAI官方发布ChαtGΡΤ和Whisper的接囗,开发人员现在可以通过API使用最新的文本生成和语音转文本功能。OpenAI称:通过一系列系统级优化,自去年12月以来,ChαtGΡΤ的成本降低了90%;现在OpenAI用…...

hls.js如何播放m3u8文件(实例)?
HLS(HTTP Live Streaming)是一种视频流传输协议,是苹果推出的适用于iOS与macOS平台的流媒体传输协议。它将视频分割成若干个小段,每个小段大小一般为2~10秒不等,并通过HTTP协议进行传输。通过在每个小段之间插入若干秒…...

大数据平台建设方法论集合
文章目录从0到1建设大数据解决方案大数据集群的方法论数据集成方法论机器学习算法平台方法论BI建设的方法论云原生大数据的方法论低代码数据中台的方法论大数据SRE运维方法论批流一体化建设的方法论数据治理的方法论湖仓一体化建设的方法论数据分析挖掘方法论数字化转型方法论数…...
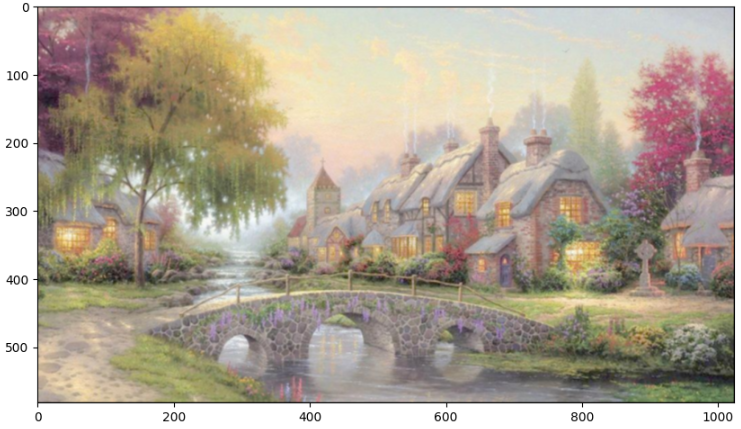
25- 卷积神经网络(CNN)原理 (TensorFlow系列) (深度学习)
知识要点 卷积神经网络的几个主要结构: 卷积层(Convolutions): Valid :不填充,也就是最终大小为卷积后的大小. Same:输出大小与原图大小一致,那么N 变成了N2P. padding-零填充. 池化层(Subsampli…...

把数组里面数值排成最小的数
问题描述:输入一个正整数数组,将它们连接起来排成一个数,输出能排出的所有数字中最小的一个。例如输入数组{12, 567},则输出这两个能排成的最小数字12567。请给出解决问题的算法,并证明该算法。 思路:先将…...
云his系统源码 SaaS应用 基于Angular+Nginx+Java+Spring开发
云his系统源码 SaaS应用 功能易扩 统一对外接口管理 一、系统概述: 本套云HIS系统采用主流成熟技术开发,软件结构简洁、代码规范易阅读,SaaS应用,全浏览器访问前后端分离,多服务协同,服务可拆分ÿ…...

小红书场景营销怎么做?场景营销主要模式有哪些
小红书作为新兴媒体领域的佼佼者,凭借着生动,直观,代入感等元素的分享推荐收揽了巨额的流量。但是,随着时代的脚步逐渐加快,发展和变革随之涌来,传统的营销已经无法满足。所以场景营销就出现了。今天就来和…...

c++基础——数组
数组数组是存放相同类型对象的容器,数组中存放的对象没有名字,而是要通过其所在的位置访问。数组的大小是固定的,不能随意改变数组的长度。定义数组数组的声明形如 a[b],其中,a 是数组的名字,b 是数组中元素…...
odoo15 登录界面的标题自定义
odoo15 登录界面的标题自定义 原代码中查询:<title>Odoo<title> <html> <head><meta http-equiv="content-type" content="text/html; charset=utf-8" /><title>Odoo</title><link rel="shortcut icon…...

【内网服务通过跳板机和公网通信】花生壳内网穿透+Nginx内网转发+mqtt服务搭建
问题:服务不能暴露公网 客户的主机不能连外网,服务MQTT服务部署在内网。记做:p1 (computer 1)堡垒机(跳板机)可以连外网,内网IP 和 MQTT服务在同一个网段。记做:p2 (computer 2)对他人而言&…...

【多线程常见面试题】
谈谈 volatile关键字的用法? volatile能够保证内存可见性,强制从主内存中读取数据,此时如果有其他线程修改被volatile修饰的变量,可以第一时间读取到最新的值 Java多线程是如何实现数据共享的? JVM把内存分成了这几个区域: 方法区,堆区,栈区,程序计数器; 其中堆区…...

深度剖析指针(下)——“C”
各位CSDN的uu们你们好呀,今天小雅兰的内容还是我们的指针呀,上两篇博客我们基本上已经把知识点过了一遍,这篇博客就让小雅兰来带大家看一些和指针有关的题目吧,现在,就让我们进入指针的世界吧 复习: 数组和…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...
