当前位置： 首页 > news >正文

Linux之磁盘分区，挂载

news 2025/7/2 19:45:53

Linux分区

分区介绍

对linux来说无论有几个分区，分给哪个目录使用，归根结底只有一个根目录，linux中每个分区都是用来组成整个文件系统的一部分。
linux采用“载入"的处理方法，他的整个文件系统中包含一整套的文件和目录，将一个分区和一个目录联系起来。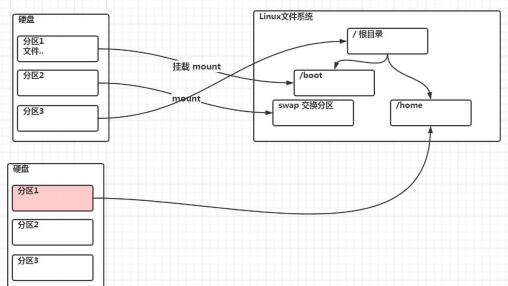
image.png

硬盘说明

如果是虚拟机一般使用SDA硬盘(SCSI硬盘接口协议的）
SCSI类的硬盘标识为sdx~,使用sd标识分区所在设备的类型，”x“表示盘号（a为基本盘，b为基本从属盘，c为辅助主盘，d为辅助从属盘），”~“代表分区，前四个分区用数字1到4表示，他们是主分区或扩展分区，从5开始就是逻辑分区。例如sda3表示为第一个SCSI硬盘上的第三个分区，sdb2表示第二个SCSI硬盘上的第二个分区。

查看所有设备挂载情况
lsblk 或者 lsblk -f

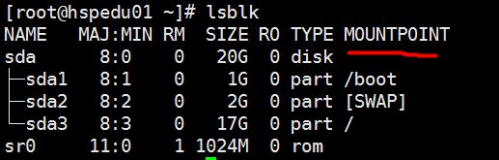
image.png

挂载

如何增加一块硬盘

  1. 虚拟机添加硬盘
  2. 分区
  3. 格式化
  4. 挂载
  5. 设置可以自动挂载
虚拟机添加硬盘

在虚机菜单中，选择【设置】,然后设备列表中添加硬盘，然后一路下一步，中间只有选择磁盘大小的地方需要修改。然后重启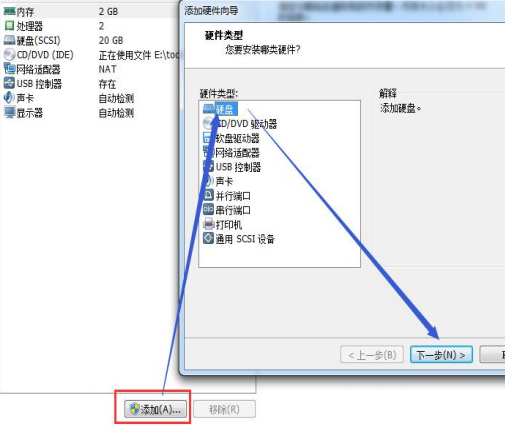
image.png

分区
fdisk /dev/sdb

开始对sdb分区

  • m：显示命令列表
  • p：显示磁盘分区 同 fdisk -l
  • n：新增分区
  • d：删除分区
  • w：写入并退出

说明：开始分区后输入n，新增分区，然后选择p，分区类型为主分区。两次回车默认剩余全部空间。最后输入w写入分区并退出，如不保存退出输入q

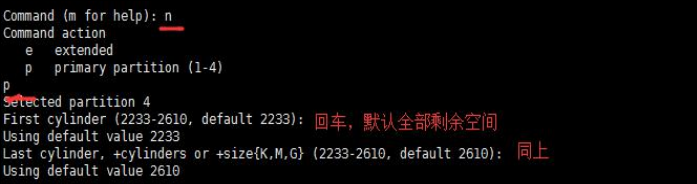
image.png

格式化磁盘
mkfs -t ext4 /dev/sdb1

其中ext4是分区类型

挂载

将一个分区与一个目录联系起来

mount 设备名 挂载目录
例如：
mount /dev/sdb1 /newdisk

解除挂载使用unmount

注意：使用命令行方式挂载，重启以后会失效

永久挂载

通过修改/etc/fstab失效挂载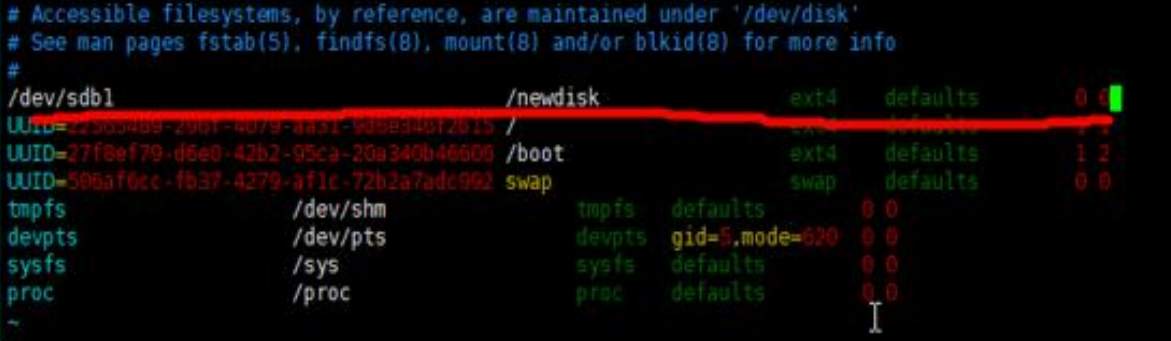
image.png
添加完成后，执行mount -a即可生效

磁盘情况查询

查询系统整体磁盘使用情况
df -h

查询系统整体磁盘的使用情况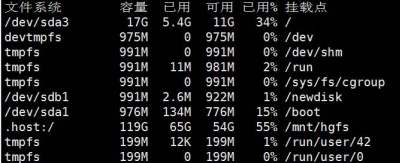
image.png

查询指定目录的磁盘占用情况
du -h

查询指定目录的磁盘占用情况，默认为当前目录

  • -s：指定目录占用大小汇总
  • -h：带计量单位
  • -a：含文件
  • –max-depth=1：子目录深度
  • -c：列出明细的同时，增加汇总值

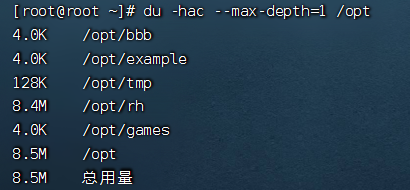
image.png

磁盘-工作常用指令

  1. 统计/opt文件夹下文件的个数
  2. 统计/opt文件夹下目录的个数
  3. 统计/opt文件夹下文件的个数，包括子文件夹里的
  4. 统计/opt文件夹下目录的个数，包括子文件夹里的

相关文章：

Linux之磁盘分区，挂载

Linux分区 分区介绍 对linux来说无论有几个分区，分给哪个目录使用，归根结底只有一个根目录，linux中每个分区都是用来组成整个文件系统的一部分。linux采用“载入"的处理方法，他的整个文件系统中包含一整套的文件和目录&…...

编程日记 2023/12/31 16:41:28

2核2G3M服务器上传速度多少？以阿里云和腾讯云为例

2核2G3M服务器上传速度多少？上传是按10M带宽算，上传速度是1280KB/秒，即1.25M/秒；下载速度按3M带宽计算，下载速度是384KB/秒。本文是以阿里云为例的，阿里云服务器当公网带宽小于10M及10M以下时，上…...

编程日记 2023/12/31 16:40:27

Cisco模拟器-OSPF路由协议

设计要求用两台双口路由器连接不同IP网段的计算机，并使用OSFP协议发现路由表使不同IP网段的计算机可以相互通信。 通过设计，可以连通IP地址网段不同的局域网，可应用在园区网的互连和互通的实现上。 主要配置步骤 路由器0： Router…...

编程日记 2023/12/31 16:36:24

SpEL 的使用

SpEL 的使用 SpEL的全称为 Spring Expression Language，具有再运行时构建复杂表达式、存取对象图属性、对象方法调用等功能 下面是一个简单样例 public class SpelTest { Test public void test1() { ExpressionParser parser new SpelExpressionParser(); …...

编程日记 2023/12/31 16:35:23

数据采集实战：电商详情页数据埋点

本文我们以电商产品的商品详情页为例，介绍如何做用户浏览以及点击行为的数据埋点。 案例中包含一个页面（商品详情页）以及该页面上的关键按钮（加购、收藏按钮），具体页面如下图所示。 （1&#xf…...

编程日记 2023/12/31 16:31:18

计算机网络——计算大题（七）

前言： 最近也是在准备计算机考试，我们的考试形式是上机考试，所以可能有些计算题是会给提供思路的，前面已经对本学期的计算机网络知识有了一个简单的认识与了解，现在我们就来对计算大题进行一个学习吧，这里的…...

编程日记 2023/12/31 16:28:15

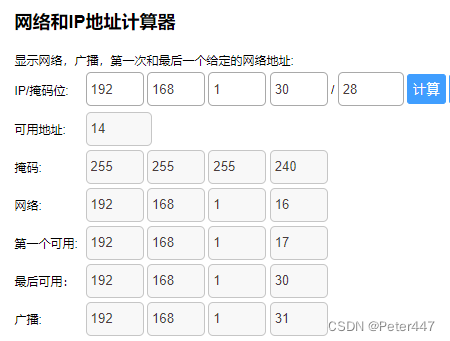
子网掩码与IP段计算

一.什么叫子网掩码： 子网掩码(subnet mask)又叫网络掩码、地址掩码、子网络遮罩，它用来指明一个IP地址的哪些位标识的是主机所在的子网，以及哪些位标识的是主机的位掩码。子网掩码不能单独存在，它必须结合IP地址一起使用。 子网掩…...

编程日记 2023/12/31 16:26:12

【译文】IEEE白皮书 6G 太赫兹技术的基本原理 2023版

第一章 简介 太赫兹波是介于微波和光波之间的光谱区域，频率从 0.1THz ~ 10THz 之间，波长在 3mm ~ 30μm 之间。提供大块连续的频带范围以满足对 Tbit/s 内极高数据传输速率的需求，使该区域成为下一代无线通信（6G）的重…...

编程日记 2023/12/31 16:25:11

AUTOSAR从入门到精通-网络通信（UDPNm）（三）

目录 前言 原理 网络状态 初始化 执行 处理器架构 时间参数...

编程日记 2023/12/31 16:24:09

ubuntu 使用openssl制作一个自签名证书

我们需要为浏览器创建自己的根CA证书来信任自签名证书。因此，让我们首先创建根CA证书 创建根CA证书 创建文件夹 mkdir openssl && cd openssl执行以下openssl命令，生成 rootCA.key 以及 rootCA.crt. 用你的域名或者ip地址替换demo.mlopshub.c…...

编程日记 2023/12/31 16:22:08

WPF+Halcon 培训项目实战(1-5):Halcon安装,图像处理,Halcon简单模板匹配

文章目录 前言相关链接项目专栏我个人对就业市场的评价Halcon安装实战1-4：Halcon基础实战5：模板匹配[形状匹配]实战代码 结尾 前言 为了更好地去学习WPFHalcon，我决定去报个班学一下。原因无非是想换个工作。相关的教学视频来源于下方的Up主…...

编程日记 2023/12/31 16:19:04

虚函数的讲解

文章目录 虚函数的声明与定义代码演示基类Person派生类Man派生类Woman 测试代码动态绑定静态绑定访问私有虚函数总结一下通过成员函数指针调用函数的方式 虚函数的声明与定义 虚函数存在于C的类、结构体等中，不能存在于全局函数中，只能作为成员函数存在…...

编程日记 2023/12/31 16:17:01

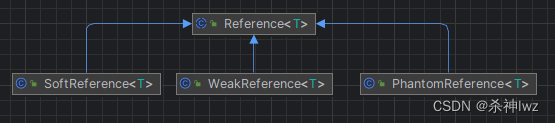
Java强软弱虚引用

面试： 1.强引用，软引用，弱引用，虚引用分别是什么？ 2.软引用和弱引用适用的场景？ 3.你知道弱引用的话，能谈谈WeakHashMap吗？ 目录 一、Java引用 1、强引用（默认支持模式…...

编程日记 2023/12/31 16:16:00

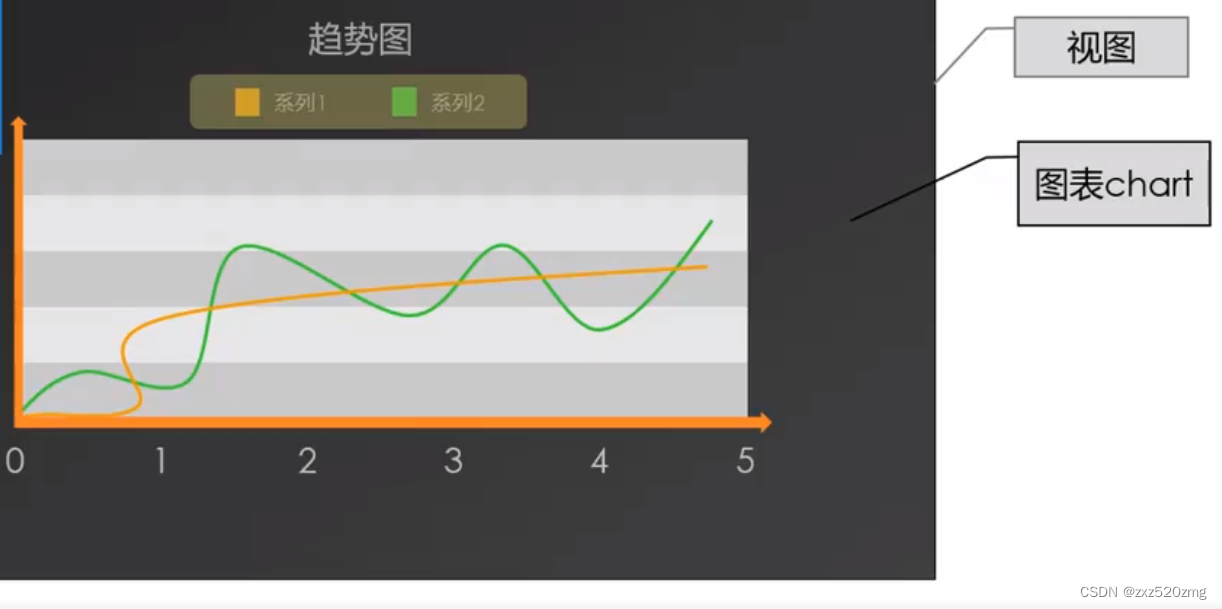
QCharView使用

QCharView概念:title、系列、图标Chart、视图 说明: 需要添加Qt组件charts 在使用QChart或者QChartView之前需要添加宏定义QT_CHARTS_USE_NAMESPACE （其实是使用了命名空间），不然不能识别QChart或者QChartView 3.在添加宏定义QT_CHARTS_USE_N…...

编程日记 2023/12/31 16:13:58

华为hcia之ipv6实验手册

R3: dhcp enable ipv6 dhcpv6 pool test address prefix 2000:23::/64 excluded-address 2000:23::2 dns-server 2000:23::2 interface GigabitEthernet0/0/0 ipv6 enable ipv6 address 2000:12::2/64 ipv6 address auto link-local undo ipv6 nd ra halt //无状态配置 inter…...

编程日记 2023/12/31 16:12:56

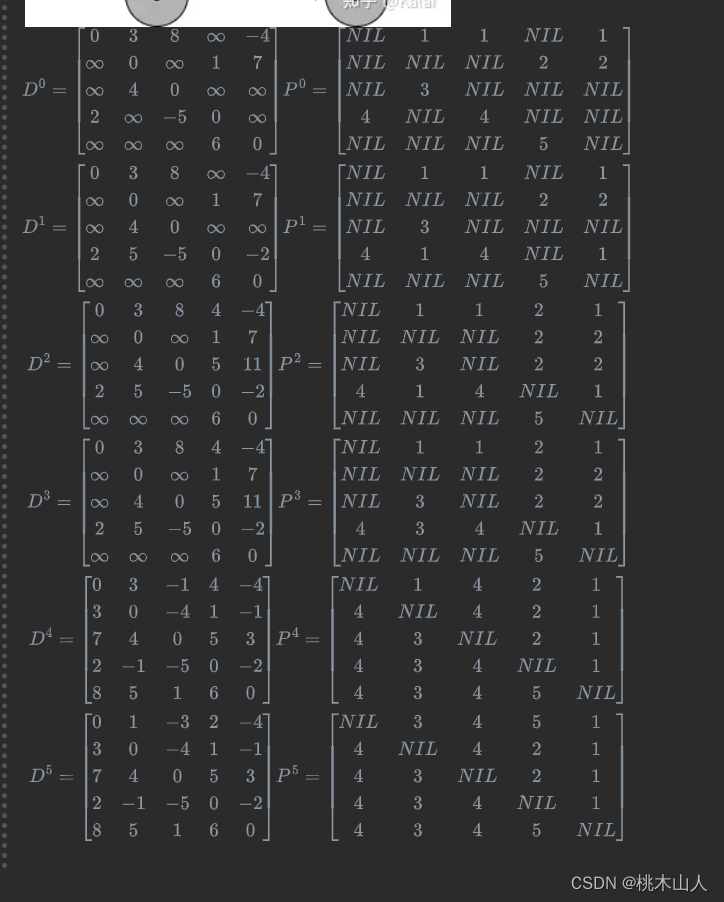
算法设计与分析-图算法小结BFS/DFS/Topologic/Dijkstra/Floyd/最大流

图 注:CSDN貌似不支持较长公式，可以复制到Markdown编辑器查看 图的表示 邻接矩阵 空间复杂度 Θ ( V 2 ) Θ(V^2) Θ(V2)邻接链表 空间复杂度 Θ ( V E ) Θ(VE) Θ(VE) BFS 邻接链表 时间复杂度 Θ ( V E ) Θ(VE) Θ(VE) void BFS(Graph G, int v) {//…...

编程日记 2023/12/31 16:11:55

CentOS 8 安装指定版本ansible

背景：想要练习ansible使用，用于面试，结果使用centos 8 的yum安装失败，提示版本不兼容（指的是python版本），故而使用python来安装指定版本的ansible，特此记录 环境：win11虚…...

编程日记 2023/12/31 16:10:53

策略模式（及案例）

策略模式 1.策略接口 定义一组算法或操作的通用接口，通常是一个抽象类或接口。该接口声明了策略类所必须实现的方法。 示例： class Strategy {doOperation() {} }2.具体策略 实现策略接口，提供具体的算法实现。每个具体策略类负责处理一…...

编程日记 2023/12/31 16:06:51

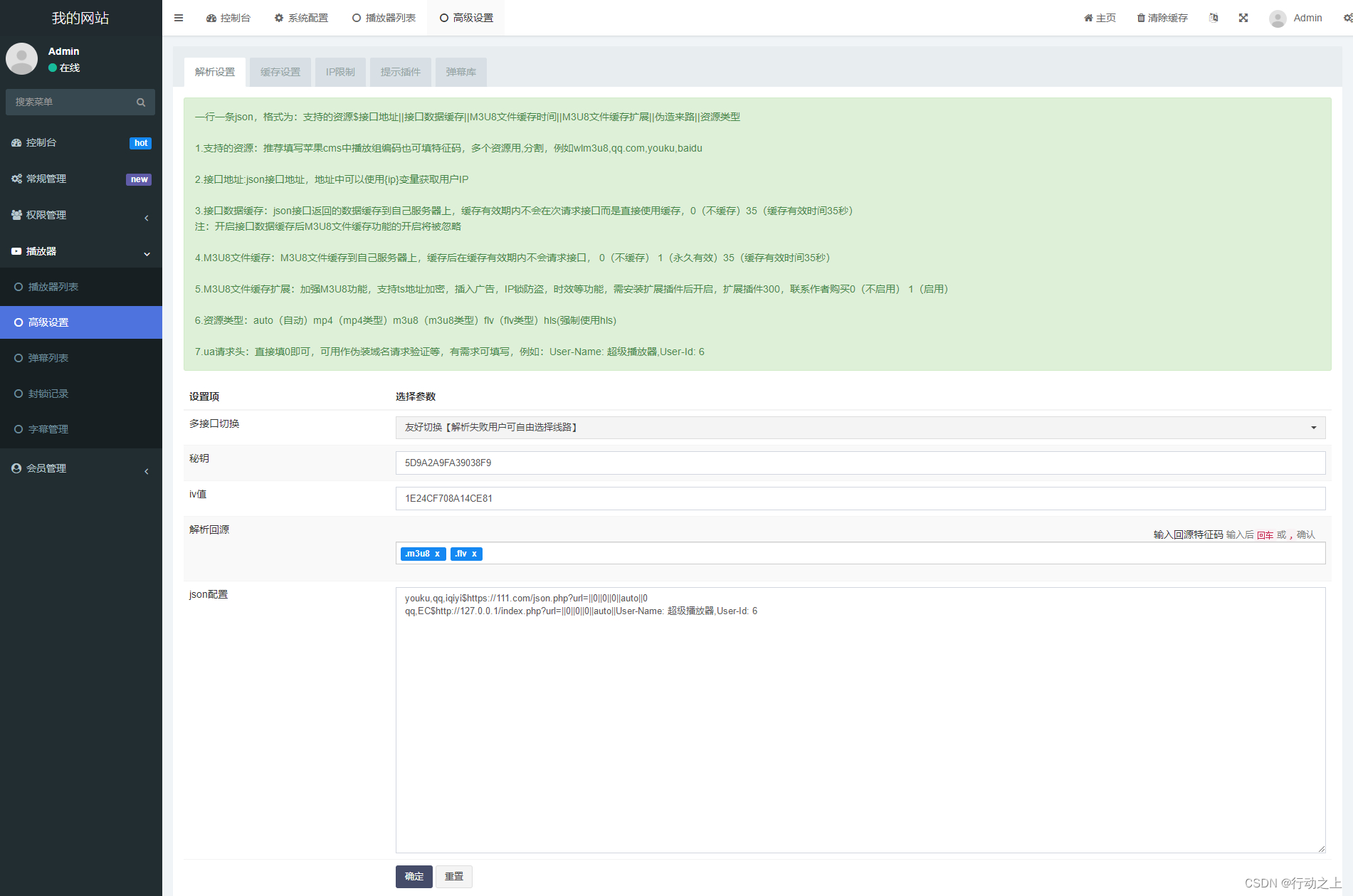
苹果CMS超级播放器专业版无授权全开源，附带安装教程

源码介绍 超级播放器专业版v1.0.8，内置六大主流播放器，支持各种格式的视频播放，支持主要功能在每一个播放器内核中都相同效果。 搭建教程 1.不兼容IE浏览器 2.php版本推荐7.4 支持7.1~7.4 3.框架引入不支持同时引入多个播放器 json对接教…...

编程日记 2023/12/31 16:05:50

项目记录：利用Redis实现缓存以提升查询效率

一、概述 当我们查询所有数据时，如果缓存中没有，则去数据库查询，如果有，直接查缓存的数据就行。注意定期更新缓存数据。 二、主体代码 private static final String ROOM_SCHEDULES_HASH "RoomSchedules";Overridepu…...

编程日记 2023/12/31 16:03:48

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)

题目：3442. 奇偶频次间的最大差值 I 思路 ：哈希，时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况，哈希表这里用数组即可实现。 C版本： class Solution { public:int maxDifference(string s) {int a[26]…...

编程新知 2025/7/2 5:27:05

【人工智能】神经网络的优化器optimizer（二）：Adagrad自适应学习率优化器

一.自适应梯度算法Adagrad概述 Adagrad（Adaptive Gradient Algorithm）是一种自适应学习率的优化算法，由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率，适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

编程新知 2025/6/30 22:45:54

循环冗余码校验CRC码 算法步骤+详细实例计算

通信过程：（白话解释） 我们将原始待发送的消息称为 M M M，依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)（意思就是 G （ x ) G（x) G（x) 是已知的）&#xff0…...

编程新知 2025/7/1 2:57:55

Python实现prophet 理论及参数优化

文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候，写过一篇简单实现，后期随着对该模型的深入研究，本次记录涉及到prophet 的公式以及参数调优，从公式可以更直观…...

编程新知 2025/6/21 6:18:34

【HTML-16】深入理解HTML中的块元素与行内元素

HTML元素根据其显示特性可以分为两大类：块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

编程新知 2025/6/21 2:24:34

select、poll、epoll 与 Reactor 模式

在高并发网络编程领域，高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表，以及基于它们实现的 Reactor 模式，为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。​ 一、I…...

编程新知 2025/6/29 23:17:49

JVM暂停（Stop-The-World，STW）的原因分类及对应排查方案

JVM暂停（Stop-The-World，STW）的完整原因分类及对应排查方案，结合JVM运行机制和常见故障场景整理而成： 一、GC相关暂停​​ 1. ​​安全点（Safepoint）阻塞​​ ​​现象​​：JVM暂停但无GC日志，日志显示No GCs detected。​​原因​​：JVM等待所有线程进入安全点（如…...

编程新知 2025/6/15 13:02:49

React---day11

14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store： 我们在使用异步的时候理应是要使用中间件的，但是configureStore 已经自动集成了 redux-thunk，注意action里面要返回函数 import { configureS…...

编程新知 2025/6/15 17:10:12

Xen Server服务器释放磁盘空间

disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

编程新知 2025/6/21 10:27:51

Python 训练营打卡 Day 47

注意力热力图可视化 在day 46代码的基础上，对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

编程新知 2025/6/22 16:30:09