算法设计与分析-图算法小结BFS/DFS/Topologic/Dijkstra/Floyd/最大流
图
注:CSDN貌似不支持较长公式,可以复制到Markdown编辑器查看
图的表示
- 邻接矩阵 空间复杂度 Θ ( V 2 ) Θ(V^2) Θ(V2)
- 邻接链表 空间复杂度 Θ ( V + E ) Θ(V+E) Θ(V+E)
BFS
-
邻接链表 时间复杂度 Θ ( V + E ) Θ(V+E) Θ(V+E)
-
void BFS(Graph G, int v) {//从顶点v出发,广度优先遍历图Gvisit(v);//访问初始顶点vsited[v] = true;//标记访问Enqueue(Q, v);//入队while (!isEmpty(Q)) {DeQueue(Q, v);//出队for (w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w))if (!visited[w]) {//w为v未访问邻接顶点visit(w);//访问visited[w] = true;//标记EnQueue(Q, w);//进队}} } -
无权最短路径问题
-
前驱子图,BFS生成树
DFS
-
递归是核心
-
void DFS(Graph G,int v){visit(v);visited[v]=true;for(w=FirstNeighbour(G,v);w>=0;w=NextNeighor(G,v,w)){if(!visited[w]){DFS(G,w);}} }
Topolpgical sort
-
拓扑排序是可以用来简单地判环的,若能则无环。
-
// deg是入度,在存图的时候需要录入数据 // A是排序后的数组 int deg[MAXN], A[MAXN]; bool toposort(int n) {int cnt = 0;queue<int> q;//若是priority_queue,则可以输出字典序最大/小拓扑序for (int i = 1; i <= n; ++i)if (deg[i] == 0)q.push(i);while (!q.empty()){int t = q.front();q.pop();A[cnt++] = t;for (auto to : edges[t]){deg[to]--;if (deg[to] == 0) // 出现了新的入度为0的点q.push(to);}}return cnt == n;// }
最小生成树
- [Kruskal][https://blog.csdn.net/yf_li123/article/details/75195549] , [Prim算法][https://blog.csdn.net/yf_li123/article/details/75148998]
单源最短路径
- Bellman-Ford
//检测有无负环
//spfa可以计算有负环 单元最短路径
void bellman_ford()
{memset(dist, 0x3f, sizeof dist);dist[1] = 0;for (int i = 0; i < k; i ++ ){memcpy(last, dist, sizeof dist);for (int j = 0; j < m; j ++ ){auto e = edges[j];dist[e.b] = min(dist[e.b], last[e.a] + e.c);}}
}
- [Topological-sort][https://blog.csdn.net/dragon8462_/article/details/119746134]
//只能有向无环图
-
Dijisktra[Dijkstra算法介绍及其优先队列优化和斐波那契堆优化][https://blog.csdn.net/qq_33903332/article/details/116095232]
//
int dijkstra()
{// 初始化, 一号点到起点的距离为0, 其他点到起点的距离为正无穷memset(dist, 0x3f, sizeof dist); dist[1] = 0;for(int i = 0; i < n -1; i ++) // n - 1迭代{int t = -1;// 找到未加到 st 集合的最短距离for(int j = 1; j <= n ; j ++)if( !st[j] && (t == -1 || dist[t] > dist[j]) )t = j;// 将t点加入到集合st[t] = true;// 更新从t出去的所有的边,他组成的路径能不能更强其他点的距离for(int j = 1; j <= n; j++)dist[j] = min(dist[j], dist[t] + w[t][j]); }
}
//堆优化
const int N = 1e5+7;
const int INF = 0x3f3f3f3f;
struct Node{int to, w;
};//to指向另一端的结点, w表示边的长度
vector<Node> g[N];//邻接表存储图
int n, m, s;//n-结点数, m-边数, s-源点
int d[N];//记录源点s到图中所有结点的最短路
bool vis[N];//在Dijkstra算法中用于记录结点是否访问
void Dijkstra_2(int s) {memset(d, 0x3f, sizeof(d));//初始距离设为INF d[s] = 0;//源点到源点的距离为 0//使用优先队列实现堆, 默认以pair的first从大到小排序priority_queue< pair<int, int> > q;q.push(make_pair(0, s));//源点放入堆中 while (!q.empty()) {pair<int, int> t = q.top(); q.pop();int from = t.second;if (vis[from]) continue;//跳过已经访问过的结点 vis[from] = true;//以该点为中间结点更新最短路径 for (int i = 0; i < g[from].size(); i++) {int to = g[from][i].to;int w = g[from][i].w;if (d[to] > d[from] + w) {d[to] = d[from] + w;if (vis[to] == false) {//first以负数存储, d小的反而大, 在堆顶 q.push(make_pair(-d[to], to));}}}}
}所有点对最短路径
-
Dijisktra跑n遍(不带负权)-Greedy -
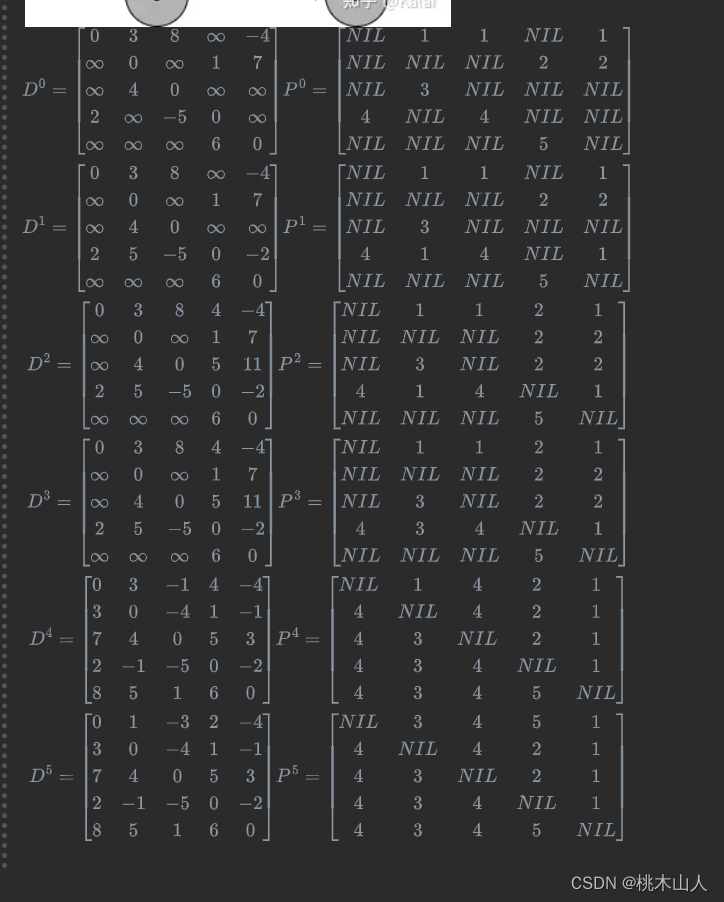
Floyd-Warshall-DP (假设权重可以为负,但不能有权重为负的环路。)d i j k d_{ij}^k dijk为从结点 $i $到 j j j 的所有中间结点全部取自集合 { 1 , 2 , . . . , k } \{1,2,...,k\} {1,2,...,k}的一条最短路径的权重。
当 k = 0 k = 0 k=0时,也就是从结点 $i $到 j j j 的路径上不包括任何结点。这样路径上只有 ( i , j ) (i,j) (i,j)这一条边,此时 d i j 0 = w ( i , j ) d_{ij}^0 = w(i,j) dij0=w(i,j)。
当 k ⩾ 1 k \geqslant 1 k⩾1时,又可以分为两种情况:
- 结点 $i $到 j j j 的最短路径 p p p,没有经过结点 k k k,此时 d i j k = d i j k − 1 d_{ij}^k = d_{ij}^{k-1} dijk=dijk−1。
- 结点 $i $到 j j j 的最短路径 p p p,经过结点了 k k k, d i j k = d i k k − 1 + d k j k − 1 d_{ij}^k = d_{ik}^{k-1} +d_{kj}^{k-1} dijk=dikk−1+dkjk−1。
D
$d_{ij}^k= \begin{cases} w(i,j)& k=0\ min{d_{ij}^{k-1}, d_{ik}^{k-1} + d_{kj}^{k-1} } & k\geqslant 1\ \end{cases}\$
PI(前驱矩阵)
$\pi_{ij}^k= \begin{cases} \pi_{ij}^{k-1} & d_{ij}^{k-1} \leqslant d_{ik}^{k-1} + d_{kj}^{k-1}\ \pi_{kj}^{k-1} & d_{ij}^{k-1} \gt d_{ik}^{k-1} + d_{kj}^{k-1}\ \end{cases}\$
FLOYD-WARSHALL(W)n = W.rowsD0 = Wlet P = n x n martix initialized with nil//前驱矩阵for i = 1 to nfor j = 1 to nif i != j and D[i, j] < ∞P[i, j] = ifor k = 1 to nDk = new n x n matrix //可以直接用两个矩阵颠倒for i=1 to nfor j= 1 to nD[ij] = min(Dk-1[ij], Dk-1[ik] + Dk-1[kj])
$$D^0 = \begin{bmatrix} 0 & 3 & 8 & \infty & -4 \ \infty & 0 & \infty & 1 & 7 \ \infty & 4 & 0 & \infty & \infty \ 2 & \infty & -5 & 0 & \infty \ \infty & \infty & \infty & 6 & 0 \ \end{bmatrix} P^0 = \begin{bmatrix} NIL & 1 & 1 & NIL & 1 \ NIL & NIL & NIL & 2 & 2 \ NIL & 3 & NIL & NIL & NIL \ 4 & NIL & 4 & NIL & NIL \ NIL & NIL & NIL & 5 & NIL \ \end{bmatrix}\ D^1 = \begin{bmatrix} 0 & 3 & 8 & \infty & -4 \ \infty & 0 & \infty & 1 & 7 \ \infty & 4 & 0 & \infty & \infty \ 2 & 5 & -5 & 0 & -2 \ \infty & \infty & \infty & 6 & 0 \ \end{bmatrix} P^1 = \begin{bmatrix} NIL & 1 & 1 & NIL & 1 \ NIL & NIL & NIL & 2 & 2 \ NIL & 3 & NIL & NIL & NIL \ 4 & 1 & 4 & NIL & 1 \ NIL & NIL & NIL & 5 & NIL \ \end{bmatrix}\ D^2 = \begin{bmatrix} 0 & 3 & 8 & 4 & -4 \ \infty & 0 & \infty & 1 & 7 \ \infty & 4 & 0 & 5 & 11 \ 2 & 5 & -5 & 0 & -2 \ \infty & \infty & \infty & 6 & 0 \ \end{bmatrix} P^2 = \begin{bmatrix} NIL & 1 & 1 & 2 & 1 \ NIL & NIL & NIL & 2 & 2 \ NIL & 3 & NIL & 2 & 2 \ 4 & 1 & 4 & NIL & 1 \ NIL & NIL & NIL & 5 & NIL \ \end{bmatrix}\ D^3 = \begin{bmatrix} 0 & 3 & 8 & 4 & -4 \ \infty & 0 & \infty & 1 & 7 \ \infty & 4 & 0 & 5 & 11 \ 2 & 5 & -5 & 0 & -2 \ \infty & \infty & \infty & 6 & 0 \ \end{bmatrix} P^3 = \begin{bmatrix} NIL & 1 & 1 & 2 & 1 \ NIL & NIL & NIL & 2 & 2 \ NIL & 3 & NIL & 2 & 2 \ 4 & 3 & 4 & NIL & 1 \ NIL & NIL & NIL & 5 & NIL \ \end{bmatrix}\ D^4 = \begin{bmatrix} 0 & 3 & -1 & 4 & -4 \ 3 & 0 & -4 & 1 & -1 \ 7 & 4 & 0 & 5 & 3 \ 2 & -1 & -5 & 0 & -2 \ 8 & 5 & 1 & 6 & 0 \ \end{bmatrix} P^4 = \begin{bmatrix} NIL & 1 & 4 & 2 & 1 \ 4 & NIL & 4 & 2 & 1 \ 4 & 3 & NIL & 2 & 1 \ 4 & 3 & 4 & NIL & 1 \ 4 & 3 & 4 & 5 & NIL \ \end{bmatrix}\ D^5 = \begin{bmatrix} 0 & 1 & -3 & 2 & -4 \ 3 & 0 & -4 & 1 & -1 \ 7 & 4 & 0 & 5 & 3 \ 2 & -1 & -5 & 0 & -2 \ 8 & 5 & 1 & 6 & 0 \ \end{bmatrix} P^5 = \begin{bmatrix} NIL & 3 & 4 & 5 & 1 \ 4 & NIL & 4 & 2 & 1 \ 4 & 3 & NIL & 2 & 1 \ 4 & 3 & 4 & NIL & 1 \ 4 & 3 & 4 & 5 & NIL \ \end{bmatrix}\\$$
csdn好像不支持这么长的公式
可以参考算法导论或者下面的图片
最大流(流网络的最大容量问题,最小分割问题
参考:https://zhuanlan.zhihu.com/p/356840694
#include <queue>
#include <stdio.h>
#include <cstring>
#define INF 2147483467
using namespace std;
using ll = long long;const int maxn = 520010, maxm = 520010;
int n, m, s, t;struct Edge{ll to, next, weight;
};
Edge edges[maxm];
int edge_cnt = 1, head[maxn], cur[maxn];void add(int x,int y,int w){edges[++edge_cnt].next = head[x];edges[edge_cnt].to = y;edges[edge_cnt].weight = w;head[x] = edge_cnt;
}int level[maxn];
bool bfs(){memset(level, 0, sizeof(level));memcpy(cur, head, sizeof(head));queue<int> q;q.push(s);level[s] = 1;while (!q.empty()){int u = q.front();q.pop();for (int i = head[u]; i != 0; i = edges[i].next){ll v = edges[i].to, flow = edges[i].weight;if (flow > 0 && level[v] == 0){level[v] = level[u] + 1;q.push(v);}} }return (level[t] != 0);
}int dfs(int p = s, int cur_flow = INF){if (p == t) return cur_flow;ll ret = 0;for (int i = cur[p]; i != 0; i = edges[i].next){cur[p] = i;ll v = edges[i].to, vol = edges[i].weight;if (level[v] == level[p] + 1 && vol > 0){int f = dfs(v, min(cur_flow - ret, vol));edges[i].weight -= f;edges[i^1].weight += f;ret += f;if (ret == cur_flow) return ret;}}return ret;
}ll dinic(){ll max_flow = 0;while (bfs()){max_flow += dfs();}return max_flow;
}int main(){scanf("%d %d %d %d", &n, &m, &s, &t);for (int i = 1; i <= m ; ++i){int x, y, w;scanf("%d %d %d", &x, &y, &w);add(x, y, w);add(y, x, 0);}printf("%lld", dinic());return 0;
}
相关文章:
算法设计与分析-图算法小结BFS/DFS/Topologic/Dijkstra/Floyd/最大流
图 注:CSDN貌似不支持较长公式,可以复制到Markdown编辑器查看 图的表示 邻接矩阵 空间复杂度 Θ ( V 2 ) Θ(V^2) Θ(V2)邻接链表 空间复杂度 Θ ( V E ) Θ(VE) Θ(VE) BFS 邻接链表 时间复杂度 Θ ( V E ) Θ(VE) Θ(VE) void BFS(Graph G, int v) {//…...

CentOS 8 安装指定版本ansible
背景:想要练习ansible使用,用于面试,结果使用centos 8 的yum安装失败,提示版本不兼容(指的是python版本),故而使用python来安装指定版本的ansible,特此记录 环境:win11虚…...
)
策略模式(及案例)
策略模式 1.策略接口 定义一组算法或操作的通用接口,通常是一个抽象类或接口。该接口声明了策略类所必须实现的方法。 示例: class Strategy {doOperation() {} }2.具体策略 实现策略接口,提供具体的算法实现。每个具体策略类负责处理一…...
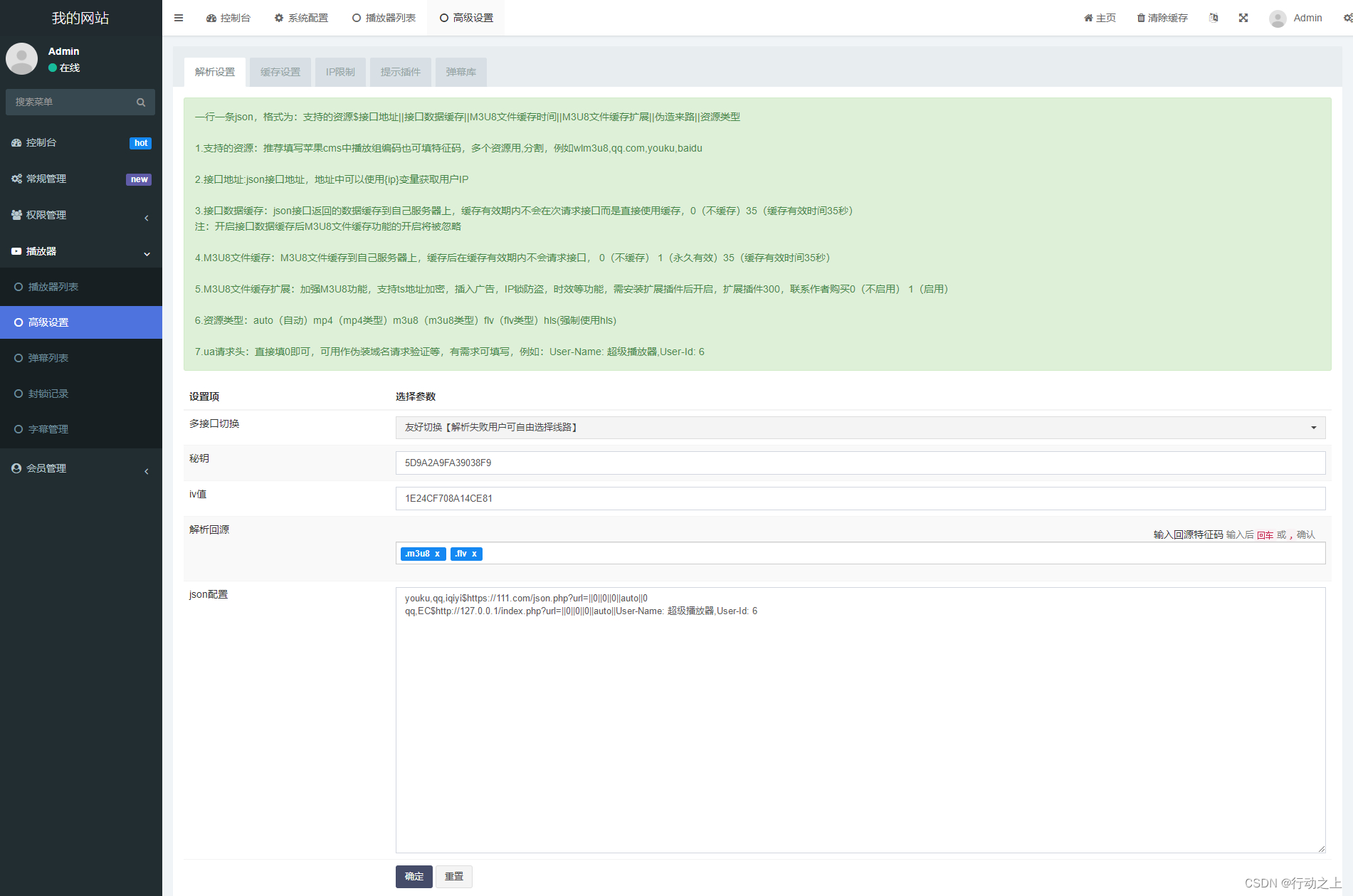
苹果CMS超级播放器专业版无授权全开源,附带安装教程
源码介绍 超级播放器专业版v1.0.8,内置六大主流播放器,支持各种格式的视频播放,支持主要功能在每一个播放器内核中都相同效果。 搭建教程 1.不兼容IE浏览器 2.php版本推荐7.4 支持7.1~7.4 3.框架引入不支持同时引入多个播放器 json对接教…...

项目记录:利用Redis实现缓存以提升查询效率
一、概述 当我们查询所有数据时,如果缓存中没有,则去数据库查询,如果有,直接查缓存的数据就行。注意定期更新缓存数据。 二、主体代码 private static final String ROOM_SCHEDULES_HASH "RoomSchedules";Overridepu…...
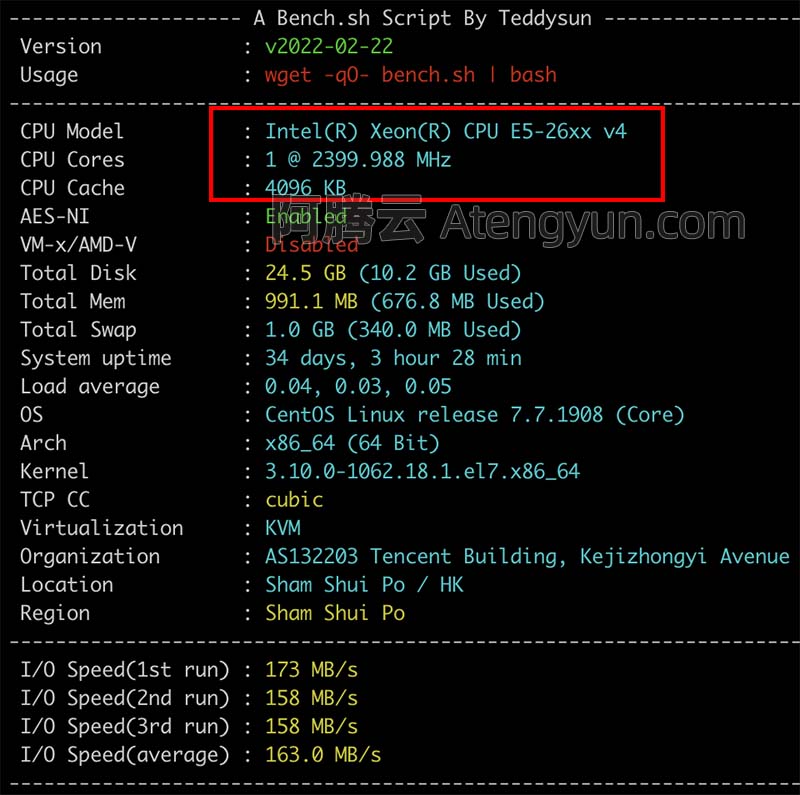
腾讯云16核32G28M轻量服务器CPU流量性能测评
腾讯云轻量16核32G28M服务器28M公网带宽下载速度峰值可达3584KB/s,折合3.5M/秒,系统盘为380GB SSD盘,6000GB月流量,折合每天200GB流量。腾讯云百科txybk.com来详细说下腾讯云轻量应用服务器16核32G28M配置性能、CPU主频型号、公网…...
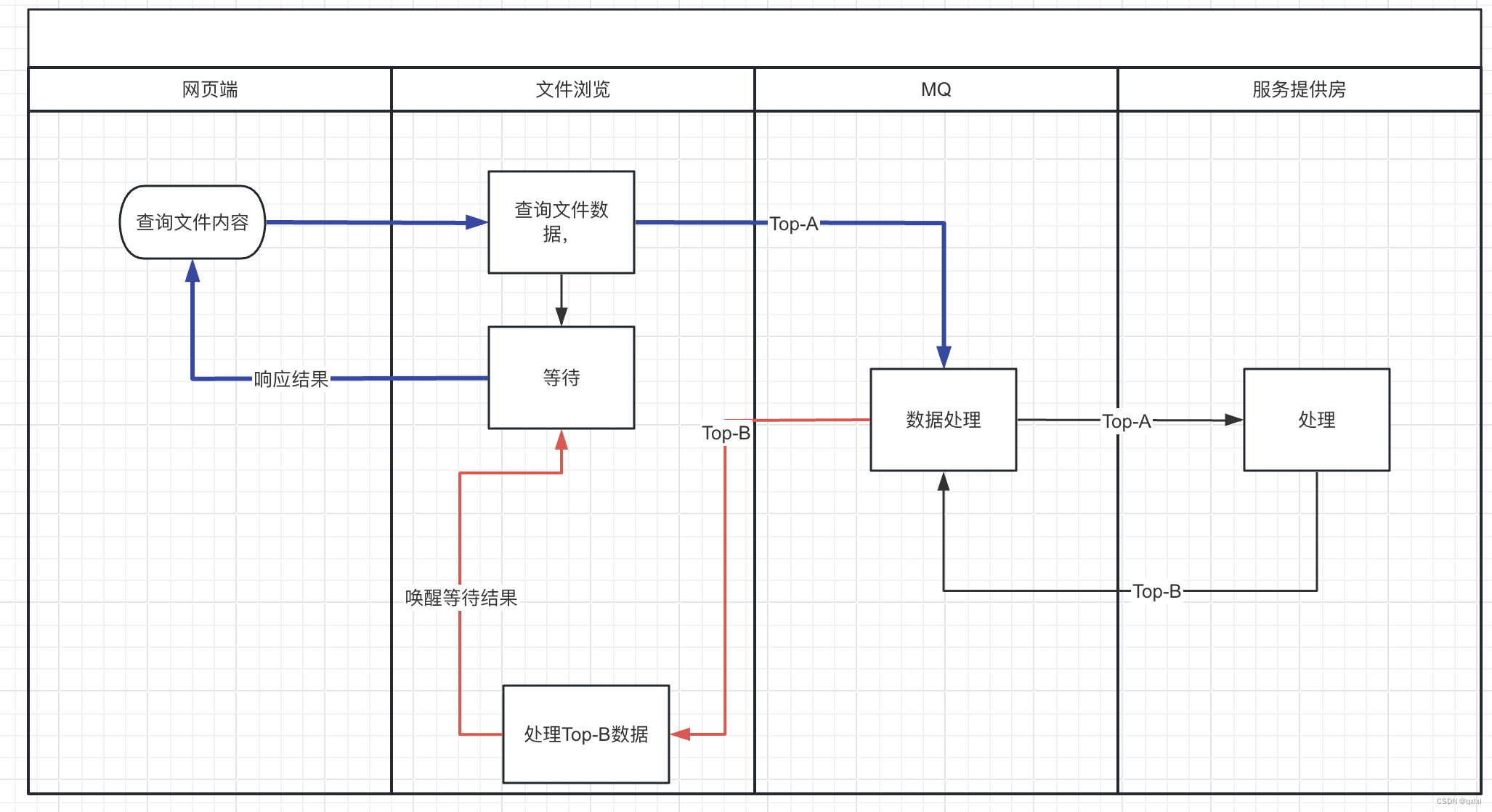
【并发设计模式】聊聊等待唤醒机制的规范实现
在多线程编程中,其实就是分工、协作、互斥。在很多场景中,比如A执行的过程中需要同步等待另外一个线程处理的结果,这种方式下,就是一种等待唤醒的机制。本篇我们来讲述等待唤醒机制的三种实现,以及对应的应用场景。 G…...

CentOS:docker同一容器间通信
docker同一容器中不同服务以别名访问 1、创建bridge网络 docker network create testnet 2、查看Docker网络 docker network ls 3、运行容器连接到testnet网络 使用方法:docker run -it --name <容器名> —network --network-alias <网络别名> <…...
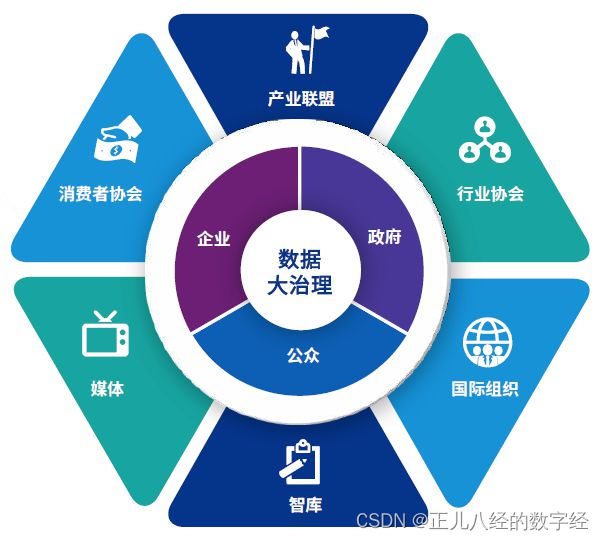
数据治理:释放数据价值的关键
随着数字化时代的到来,数据已成为组织和企业最重要的资产之一。然而,数据的快速增长和复杂性也给数据管理带来了巨大的挑战。为了确保数据的质量、安全性和合规性,数据治理已成为组织和企业必须面对的重要问题。数据治理是数据要素市场建设的…...

新手快速上手掌握基础排序<一>
听说看到日落金山的人,接下来的日子会顺顺利利,万事胜意,生活明朗-----------林辞忧 引言 从基础的两数交换排序,三四个数排序输出,到学习入门级的排序方法,如冒泡法,选择法,再学…...

2023年03月21日_chatgpt宕机事件的简单回顾
你能想象吗 ChatGPT挂了 昨天半夜呢 来自全球各地的用户纷纷发现 ChatGPT的网站弹出了报错警告的信息 然后立即就无法使用了 即使是有特权的plus账户也未能幸免 一时之间呢 chatgptdown的话题在Twitter刷屏 不少重度的用户表示很着急 有的用户说呢没了ChatGPT 这工作…...
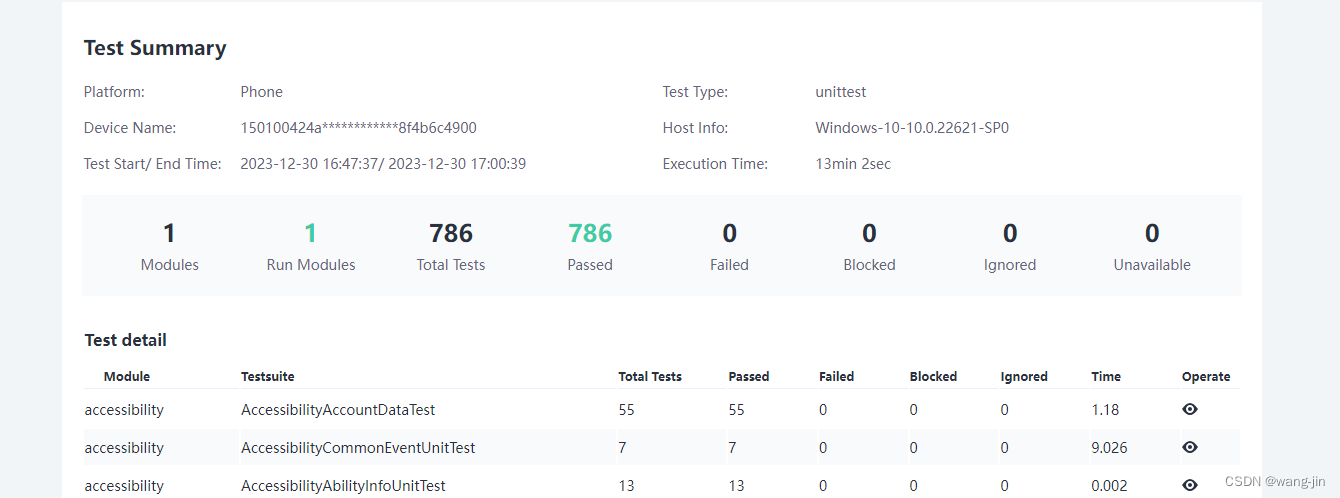
RK3568测试tdd
RK3568测试tdd 一、门禁取包二、烧录三、跑tdd用例四、查看结果参考资料 一、门禁取包 右键复制链接,粘贴下载;解压到文件夹; 二、烧录 双击\windows\RKDevTool.exe打开烧写工具,工具界面击烧写步骤如图所示: 推荐…...
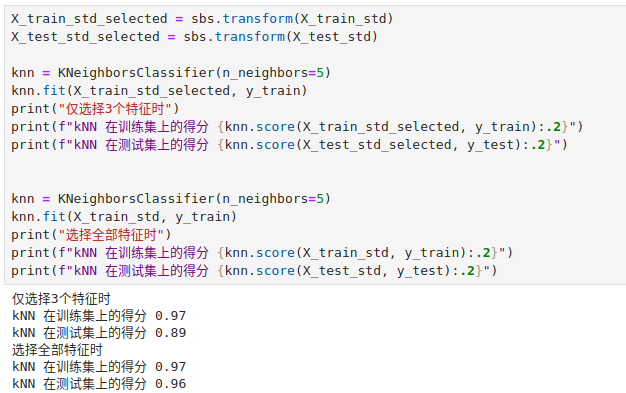
机器学习系列13:通过随机森林获取特征重要性
我们已经知道通过 L1 正则化和 SBS 算法可以用来做特征选择。 我们还可以通过随机森林从数据集中选择相关的特征。随机森林里面包含了多棵决策树,我们可以通过计算特征在每棵决策树决策过程中所产生的的信息增益平均值来衡量该特征的重要性。 你可能需要参考&…...

flink中值得监控的几个指标
背景 为了维持flink的正常运行,对flink的日常监控就变得很重要,本文我们就来看一下flink中要监控的几个重要的指标 重要的监控指标 1.算子的处理速度的指标:numRecordsInPerSecond/numRecordsOutPerSecond,这有助于你了解到算子的是否正在…...

最优化方法Python计算:无约束优化应用——逻辑分类模型
逻辑回归模型更多地用于如下例所示判断或分类场景。 例1 某银行的贷款用户数据如下表: 欠款(元)收入(元)是否逾期17000800Yes220002500No350003000Yes440004000No520003800No 显然,客户是否逾期ÿ…...
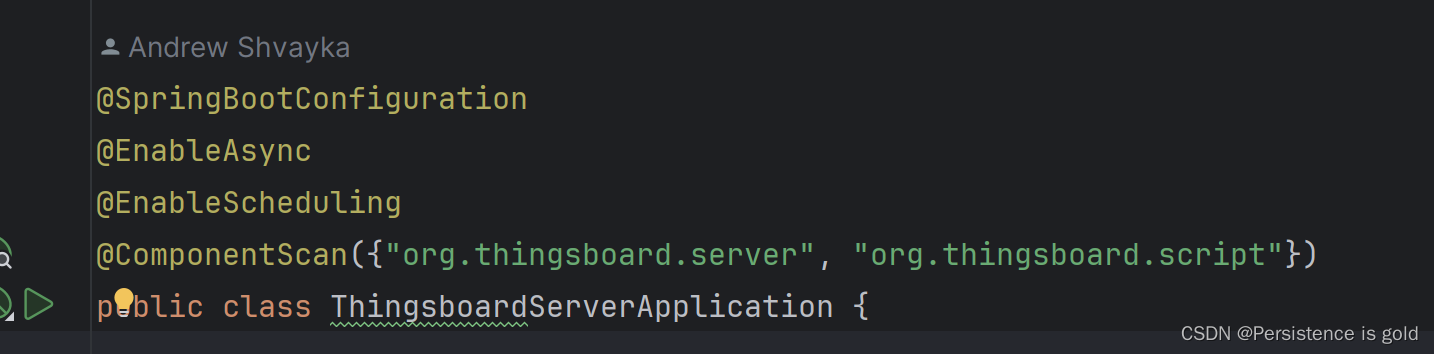
springboot定时执行某个任务
springboot定时执行某个任务 要定时执行的方法加上Schedule注解 括号内跟 cron表达式 “ 30 15 10 * * ?” 代表秒 分 时 日 月 周几 启动类上加上EnableScheduling 注释...

Java EE Servlet之Servlet API详解
文章目录 1. HttpServlet1.1 核心方法 2. HttpServletRequest3. HttpServletResponse 接下来我们来学习 Servlet API 里面的详细情况 1. HttpServlet 写一个 Servlet 代码,都是要继承这个类,重写里面的方法 Servlet 这里的代码,只需要继承…...

neo4j运维管理
管理数据库 概念 Neo4j 5(从v4.0),可以同时创建和使用多个活动数据库。 DBMS Neo4j是一个数据库管理系统(DBMS),能够管理多个数据库。DBMS可以管理一个独立的服务器,也可以管理集群中的一组服务器。 实例 Neo4j实例是运行Neo4j服务器代…...
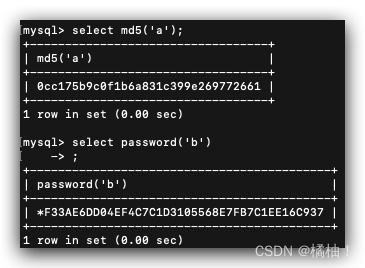
【MYSQL】-函数
💖作者:小树苗渴望变成参天大树🎈 🎉作者宣言:认真写好每一篇博客💤 🎊作者gitee:gitee✨ 💞作者专栏:C语言,数据结构初阶,Linux,C 动态规划算法🎄 如 果 你 …...
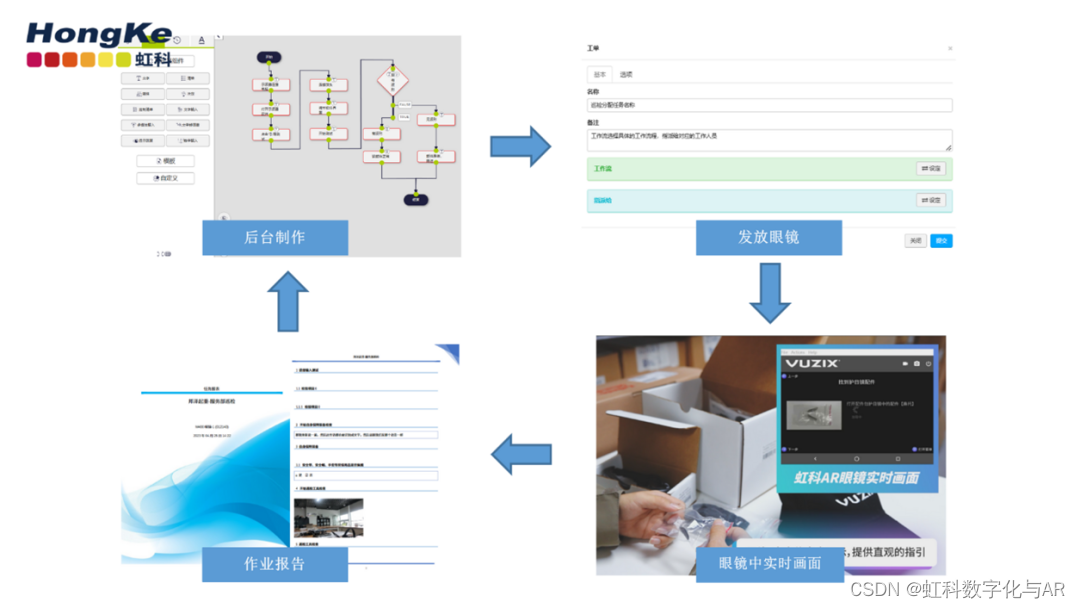
传统船检已经过时?AR智慧船检来助力!!
想象一下,在茫茫大海中,一艘巨型货轮正缓缓驶过。船上的工程师戴着一副先进的AR眼镜,他们不再需要反复翻阅厚重的手册,一切所需信息都实时显示在眼前。这不是科幻电影的场景,而是智慧船检技术带来的现实变革。那么问题…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...
