学习动态规划解决不同路径、最小路径和、打家劫舍、打家劫舍iii
学习动态规划|不同路径、最小路径和、打家劫舍、打家劫舍iii
62 不同路径

- 动态规划,dp[i][j]表示从左上角到(i,j)的路径数量
- dp[i][j] = dp[i-1][j] + dp[i][j-1]


import java.util.Arrays;/*** 路径数量* 动态规划,dp[i][j]表示从左上角到(i,j)的路径数量* dp[i][j] = dp[i-1][j] + dp[i][j-1]*/
public class $62 {public int uniquePaths(int m, int n) {int[][] dp = new int[m][n];//边界for (int i = 0; i < m; i++) {dp[i][0] = 1;}for (int i = 0; i < n; i++) {dp[0][i] = 1;}for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = dp[i-1][j] + dp[i][j-1];}}return dp[m-1][n-1];}public int uniquePaths2(int m, int n) {int[] dp = new int[n];Arrays.fill(dp, 1);for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[j] += dp[j-1];}}return dp[n-1];}
}
import java.util.Arrays;/*** 路径数量* 动态规划,dp[i][j]表示从左上角到(i,j)的路径数量* dp[i][j] = dp[i-1][j] + dp[i][j-1]*/
public class $62 {public int uniquePaths2(int m, int n) {int[] dp = new int[n];Arrays.fill(dp, 1);for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[j] += dp[j-1];}}return dp[n-1];}
}
64 最小路径和

- 动态规划,dp[i][j]表示从左上角到(i,j)的最小路径和
- grid[i][j] = Math.min(grid[i-1][j], grid[i][j-1]) + grid[i][j]

/*** 最小路径和* grid[i][j] = Math.min(grid[i-1][j], grid[i][j-1]) + grid[i][j]*/
public class $64 {public int minPathSum(int[][] grid) {for (int i = 0; i < grid.length; i++) {for (int j = 0; j < grid[i].length; j++) {if (i==0 && j==0) continue;else if (i!=0 && j==0) grid[i][j] = grid[i-1][j] + grid[i][j];else if (i==0 && j!=0) grid[i][j] = grid[i][j-1] + grid[i][j];else grid[i][j] = Math.min(grid[i-1][j], grid[i][j-1]) + grid[i][j];}}return grid[grid.length-1][grid[0].length-1];}
}198 打家劫舍

- 动态规划,nums[i]表示前i间房屋能偷窃到的最高总金额
- nums[i] = Math.max(nums[i-1], nums[i-2]+nums[i]);

/*** 打家劫舍* 动态规划,nums[i]表示前i间房屋能偷窃到的最高总金额* nums[i] = Math.max(nums[i-1], nums[i-2]+nums[i]);*/
public class $198 {public int rob(int[] nums) {//注意特殊值0,1if (nums == null || nums.length == 0) {return 0;}if (nums.length == 1) {return nums[0];}//nums[1]为nums[0]、nums[1]的最大值nums[1] = Math.max(nums[0], nums[1]);//从nums[2]开始for (int i = 2; i < nums.length; i++) {nums[i] = Math.max(nums[i-1], nums[i-2]+nums[i]);}return nums[nums.length-1];}
}337 打家劫舍iii

- 树形动态规划
- 我们可以用 f(o)表示选择 o节点的情况下,o节点的子树上被选择的节点的最大权值和;
- g(o)表示不选择 o节点的情况下,o节点的子树上被选择的节点的最大权值和;
- l 和 r代表 o 的左右孩子。
- 当 o 被选中时:o 的左右孩子都不能被选中,
-
故 o 被选中情况下子树上被选中点的最大权值和为 l和 r不被选中的最大权值和 + o的值 -
f(o)=g(l)+g(r)+o.val - 当 o不被选中时,o的左右孩子可以被选中,也可以不被选中。
-
对于 o的某个具体的孩子 x,它对 o 的贡献是 x被选中和不被选中情况下权值和的较大值。 -
g(o)=max{f(l),g(l)} + max{f(r),g(r)}

import java.util.HashMap;
import java.util.Map;/*** 打家劫舍iii* 树形动态规划* 我们可以用 f(o)表示选择 o节点的情况下,o节点的子树上被选择的节点的最大权值和;* g(o)表示不选择 o节点的情况下,o节点的子树上被选择的节点的最大权值和;* l 和 r代表 o 的左右孩子。** 当 o 被选中时:o 的左右孩子都不能被选中,* 故 o 被选中情况下子树上被选中点的最大权值和为 l和 r不被选中的最大权值和 + o的值* f(o)=g(l)+g(r)+o.val* 当 o不被选中时,o的左右孩子可以被选中,也可以不被选中。* 对于 o的某个具体的孩子 x,它对 o 的贡献是 x被选中和不被选中情况下权值和的较大值。* g(o)=max{f(l),g(l)} + max{f(r),g(r)}*/
public class $337 {Map<TreeNode, Integer> f = new HashMap<>();Map<TreeNode, Integer> g = new HashMap<>();public int rob(TreeNode root) {process(root);return Math.max(f.getOrDefault(root, 0), g.getOrDefault(root, 0));}private void process(TreeNode root) {if (root == null) {return;}process(root.left);process(root.right);f.put(root, root.val + g.getOrDefault(root.left, 0) + g.getOrDefault(root.right, 0));g.put(root, Math.max(f.getOrDefault(root.left, 0), g.getOrDefault(root.left, 0))+ Math.max(f.getOrDefault(root.right, 0), g.getOrDefault(root.right, 0)));}//法一的简化版public int rob2(TreeNode root) {int[] rootStatus = process2(root);return Math.max(rootStatus[0], rootStatus[1]);}private int[] process2(TreeNode root) {if (root == null) {return new int[]{0, 0};}int[] l = process2(root.left);int[] r = process2(root.right);int selected = root.val + l[1] + r[1];int notSelected = Math.max(l[0], l[1]) + Math.max(r[0], r[1]);return new int[]{selected, notSelected};}
}相关文章:

学习动态规划解决不同路径、最小路径和、打家劫舍、打家劫舍iii
学习动态规划|不同路径、最小路径和、打家劫舍、打家劫舍iii 62 不同路径 动态规划,dp[i][j]表示从左上角到(i,j)的路径数量dp[i][j] dp[i-1][j] dp[i][j-1] import java.util.Arrays;/*** 路径数量* 动态规划,dp[i][j]表示从左上角到(i,j)的路径数量…...

nodejs微信小程序+python+PHP特困救助供养信息管理系统-计算机毕业设计推荐
目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性:…...

Vue(二):计算属性与 watch 监听器
03. Vue 指令拓展 3.1 指令修饰符 可以通过 . 来指明一些指令的后缀,不同的后缀中封装了不同的操作,可以帮助我们简化代码,比如之前使用过的监听 enter 键的弹起,我们需要操作事件对象,来检测用户使用了哪个键&#…...

25、WEB攻防——通用漏洞SQL读写注入MYSQLMSSQLPostgreSQL
文章目录 Mysql-root高权限读写注入PostgreSQL——dba高权限读写注入Mssql-sa高权限读写注入 Access无高权限注入点——只能猜解,而且是暴力猜解; MYSQL,PostgreSQL,MSSQL(SQL server)高权限注入点——可升级读写(文件…...

【第5期】前端Vue使用Proxy+Vuex(store、mutations、actions)跨域调通本地后端接口
本期简介 本期要点 本地开发前后端如何跨域调用全局请求、响应处理拦截器处理封装HTTP请求模块编写API请求映射到后端API数据的状态管理 一、 本地开发前后端如何跨域调用 众所周知,只要前端和后端的域名或端口不一样,就存在跨域访问,例如&…...
编译器中,Release和Debug区别)
在Visual Studio(VS)编译器中,Release和Debug区别
一、 优化级别 1、Debug(调试) 在Debug模式下,编译器不会对代码进行优化,而是专注于生成易于调试的代码。这使得开发者可以在调试过程中更直观地跟踪变量的值和程序的执行流程。 2、Release(发布) 在Relea…...
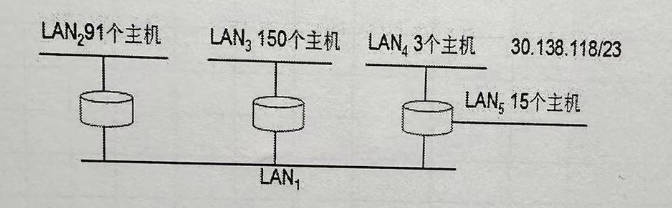
子网划分问题(实战超详解)_主机分配地址
文章目录: 子网划分的核心思想 第一步,考虑借几位作为子网号 第二步,确定子网的网络地址 第三步,明确网络地址,广播地址,可用IP地址范围 一些可能出现的疑问 实战 题目一 子网划分的核心思想 网络号不变,借用主机号来产生新的网络 划分前的网络:网络号主机号 划分后的网络:原网…...

【QT】单例模式,Q_GLOBAL_STATIC 宏的使用和使用静态成员函数,eg:{简单的日志记录器}
简单的日志记录器为例 。 创建一个Logger类,该类负责记录应用程序的日志消息 使用 Q_GLOBAL_STATIC 宏 解析:Q_GLOBAL_STATIC 是一个 Qt 宏,用于创建全局静态实例。它确保在需要时只创建一次实例,而不管该实例是在哪个线程中创建…...

利用小红书笔记详情API:构建高效的内容创作与运营体系
随着社交媒体的兴起,小红书作为国内知名的内容分享平台,吸引了大量用户和内容创作者。为了更好地获取小红书上的优质内容,许多企业和开发者选择使用小红书笔记详情API。本文将探讨如何利用该API构建高效的内容创作与运营体系。 一、小红书笔记…...
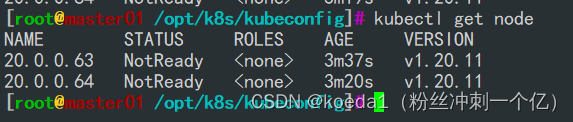
【K8S 二进制部署】部署单Master Kurbernetes集群
目录 一、基本架构和系统初始化 1、集群架构: 2、操作系统初始化配置: 2.1、关闭防火墙和安全机制: 2.2、关闭swap 2.3、根据规划设置主机名 2.4、三台主机全部互相映射 2.5、调整内核参数 3、时间同步(所有节点时间必须同…...

vue中常见的指令
简单介绍一下常见的vue中用到的指令 v-on 指定当前的事件,语法糖为,如例子所示,指定按钮的事件为addCounter,点击会使变量counter 1 <!DOCTYPE html> <html><head><meta charset"utf-8" />…...
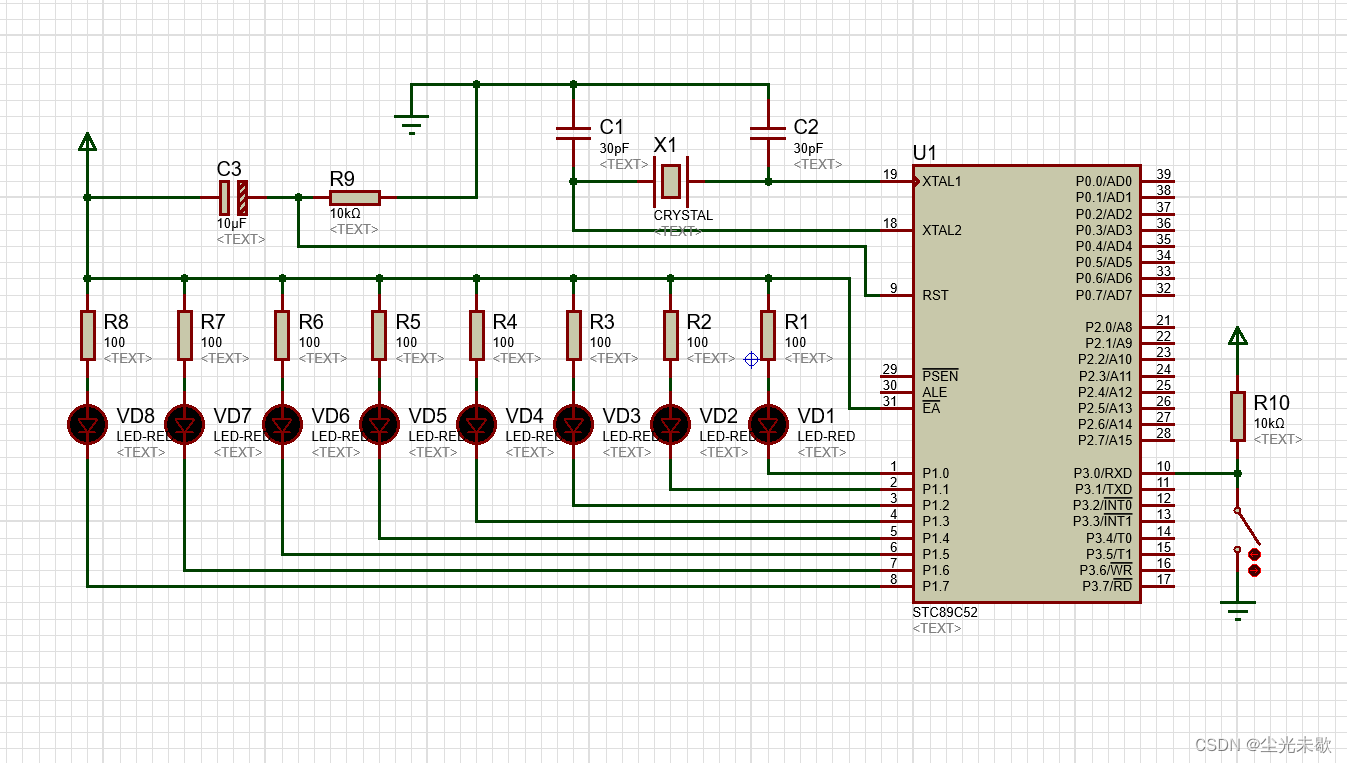
单片机原理及应用:开关控制LED多种点亮模式
从这篇文章开始,我们不再只研究单一的外设工作,而是将LED、数码管、开关、按键搭配在一起研究,这篇文章主要介绍LED和开关能擦出怎样的火花,同时也介绍一些函数封装的知识。 由于开关有闭合与打开两种状态,LED有左移流…...

你真的了解UVM sequence的运行机制吗
1. 前言 UVM在sequence里提供了很多的callback方法给用户,从而更灵活地完成各种复杂场景的交互和控制执行顺序。我们可能在很多情况下只使用了body()方法,本文将介绍sequence里常见的callback方法,以及在不同场景下,它们的是否被…...

Bug升级记
2023.12.28 (1) 小程序session_key泄露隐患 核心:session_key这个字段及对应值不应该传到小程序客户端等服务器外的环境 错误操作:直接在小程序调用https://api.weixin.qq.com/sns/jscode2session并将session_key作为参数进行明文传输 正确操…...
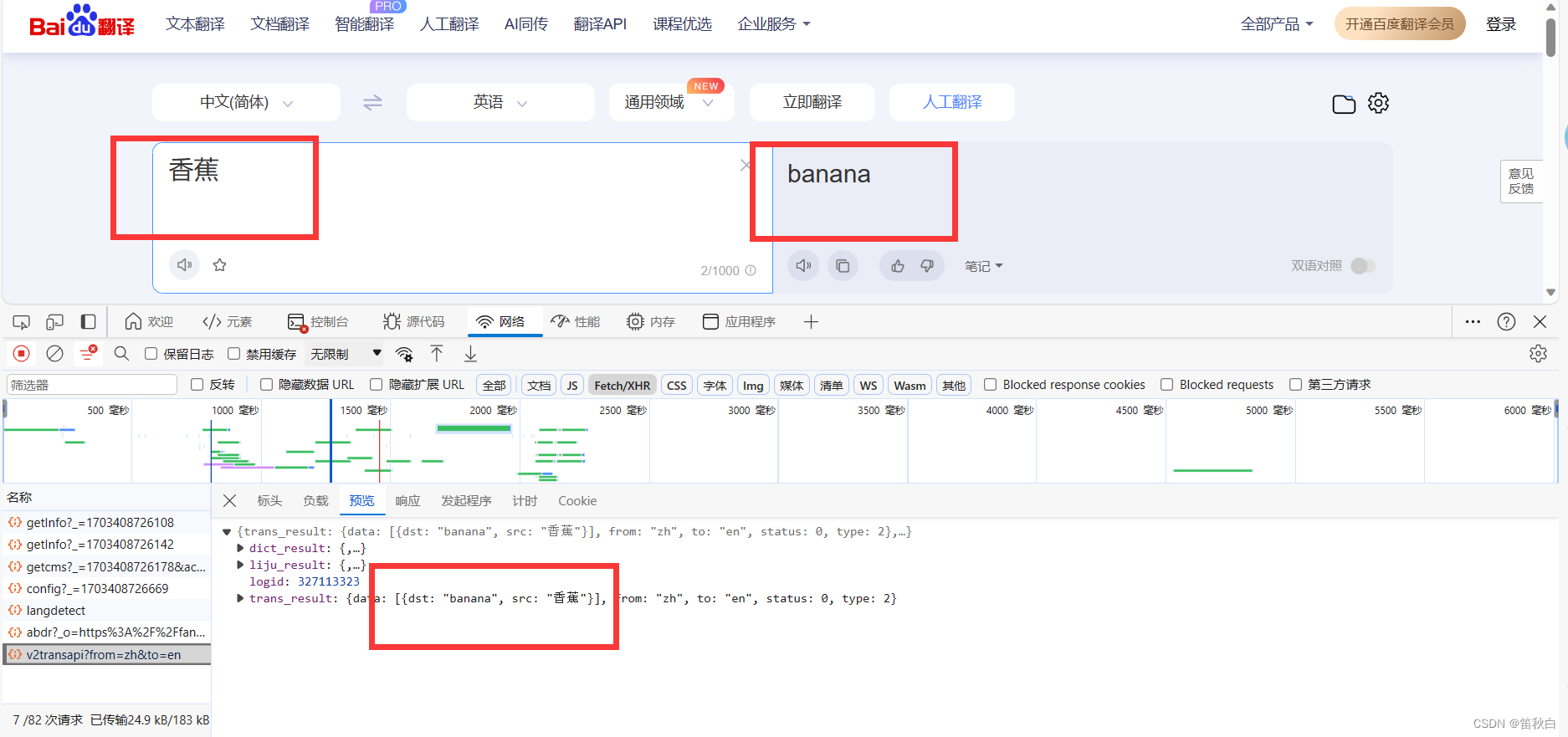
爬虫详细教程第1天
爬虫详细教程第一天 1.爬虫概述1.1什么是爬虫?1.2爬虫工具——Python1.3爬虫合法吗?1.4爬虫的矛与盾1.4.1反爬机制1.4.2反爬策略1.4.3robots.txt协议 2.爬虫使用的软件2.1使用的开发工具: 3.第一个爬虫4.web请求4.1讲解一下web请求的全部过程4.2页面渲染…...
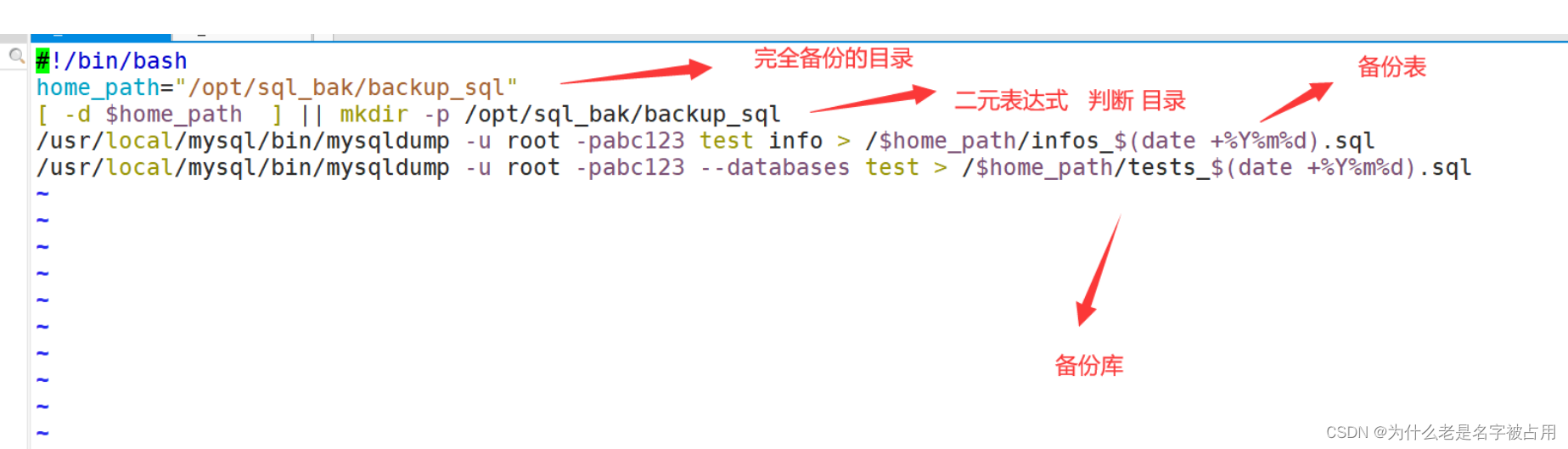
[Linux] MySQL数据库的备份与恢复
一、数据库备份的分类和备份策略 1.1 数据库备份的分类 1)物理备份 物理备份:对数据库操作系统的物理文件(如数据文件、日志文件等)的备份。 物理备份方法: 冷备份(脱机备份) :是在关闭数据库的时候进…...

Django、Python版本升级问题大汇总
Django3.0升级到4.1,Python3.8升级到3.11.6问题大汇总 报错1:ERROR: Could not build wheels for cffi, uWSGI, which is required to install pyproject.toml-based projects ERROR: Could not build wheels for cffi, uWSGI, which is required to install pyproject.tom…...

2023-12-30 AIGC-LangChain介绍
摘要: 2023-12-30 AIGC-LangChain介绍 LangChain介绍 1. https://youtu.be/Ix9WIZpArm0?t353 2. https://www.freecodecamp.org/news/langchain-how-to-create-custom-knowledge-chatbots/ 3. https://www.pinecone.io/learn/langchain-conversational-memory/ 4. https://de…...

pytorch01:概念、张量操作、线性回归与逻辑回归
目录 一、pytorch介绍1.1pytorch简介1.2发展历史1.3pytorch优点 二、张量简介与创建2.1什么是张量?2.2Tensor与Variable2.3张量的创建2.3.1 直接创建torch.tensor()2.3.2 从numpy创建tensor 2.4根据数值创建2.4.1 torch.zeros()2.4.2 torch.zeros_like()2.4.3 torch…...

storyBook play学习
场景 在官方给出的案例中, Page.stories.js import { within, userEvent } from storybook/testing-library import MyPage from ./Page.vueexport default {title: Example/Page,component: MyPage,parameters: {// More on how to position stories at: https:/…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...
