【数值分析】LU分解解Ax=b,matlab自己编程实现
LU分解(直接三角分解,Doolittle分解)
A x = b , A = L U Ax=b \,\,,\,\, A=LU Ax=b,A=LU
{ L y = b U x = y \begin{cases} Ly=b \\ Ux=y \end{cases} {Ly=bUx=y
矩阵 L {L} L 的对角元素为 1 {1} 1 ,矩阵 U {U} U 的第一行和 A {A} A 相同。
步骤:
1. 矩阵 L 的对角元素为 1 ,矩阵 U 的第一行和 A 相同。 2. 迭代 , j = 1 , 2 , ⋯ n − 1 算 L 的第 j 列 , L i , j = A i , j − ∑ r = 1 j − 1 L i , r U r , j U j , j , i = j + 1 , j + 2 , ⋯ , n 算 U 的第 j + 1 行 , U j + 1 , k = A j + 1 , k − ∑ r = 1 j L j + 1 , r U r , k L j + 1 , j + 1 , k = j + 1 , j + 2 , ⋯ , n 3. 回代 , y i = b i − ∑ j = 1 i − 1 L i , j y j , i = 1 , 2 , ⋯ , n x i = y i − ∑ j = i + 1 n x j ⋅ U i , j U i , i , i = n , n − 1 , ⋯ , 1 \begin{align*} 1.& 矩阵 L 的对角元素为 1 ,矩阵U 的第一行和A相同。 \\ \\ 2. & 迭代 \,\,,\,\, j=1,2, \cdots n-1 \\ \\ &算L的第j列 \,\,,\,\, L_{i,j}= \frac{A_{i,j}- \sum_{r=1}^{j-1}L_{i,r}U_{r,j}}{U_{j,j}},i=j+1,j+2,\cdots ,n \\ \\ &算U的第j+1行 \,\,,\,\, U_{j+1,k}= \frac{A_{j+1,k}- \sum_{r=1}^{ j}L_{j+1,r}U_{r,k}}{L_{j+1,j+1}} ,k=j+1,j+2,\cdots ,n \\ \\ 3.& 回代 \,\,,\,\, \\ \\ & y_i= b_i- \sum_{j=1}^{ i-1}L_{i,j}y_j,i=1,2,\cdots ,n \\ \\ &x_i= \frac{y_i- \sum_{j=i+1}^{ n}x_j \cdot U_{i,j}}{U_{i,i}} \,\,,\,\, i=n,n-1, \cdots ,1 \end{align*} 1.2.3.矩阵L的对角元素为1,矩阵U的第一行和A相同。迭代,j=1,2,⋯n−1算L的第j列,Li,j=Uj,jAi,j−∑r=1j−1Li,rUr,j,i=j+1,j+2,⋯,n算U的第j+1行,Uj+1,k=Lj+1,j+1Aj+1,k−∑r=1jLj+1,rUr,k,k=j+1,j+2,⋯,n回代,yi=bi−j=1∑i−1Li,jyj,i=1,2,⋯,nxi=Ui,iyi−∑j=i+1nxj⋅Ui,j,i=n,n−1,⋯,1
matlab实现
%% Ax=b例子
A = [16 -12 2 4;12 -8 6 10;3 -13 9 23;-6 14 1 -28];
b = [17 36 -49 -54]';
[x,L,U] = LUsolve(A,b)%% LU分解解Ax=b
% 输入方阵A,向量b
% 输出解x,L、U矩阵
function [x,L,U] = LUsolve(A,b)n = size(A);L = eye(n);U(1,[1:n]) = A(1,[1:end]);for j = 1:n-1 % 对U是行号,对L是列号for i = j+1:n % 算L第i行j列L(i,j) = A(i,j);for r = 1:j-1L(i,j) = L(i,j)- L(i,r)*U(r,j);endL(i,j) = L(i,j)/U(j,j);endfor k = j+1:n % 算U第j+1行k列U(j+1,k) = A(j+1,k);for r = 1:jU(j+1,k) = U(j+1,k)-L(j+1,r)*U(r,k);endU(j+1,k) = U(j+1,k)/L(j+1,j+1);endend% 回代for i = 1:ny(i) = b(i);for j = 1:i-1y(i) = y(i)-L(i,j)*y(j);endendfor i=n:-1:1 x(i) = y(i);for j=n:-1:i+1x(i) = x(i)-U(i,j)*x(j);endx(i) = x(i)/U(i,i);endx = x';
end
相关文章:

【数值分析】LU分解解Ax=b,matlab自己编程实现
LU分解(直接三角分解,Doolittle分解) A x b , A L U Axb \,\,,\,\, ALU Axb,ALU { L y b U x y \begin{cases} Lyb \\ Uxy \end{cases} {LybUxy 矩阵 L {L} L 的对角元素为 1 {1} 1 ,矩阵 U {U} U 的第一行和 A {A} A …...

华为HCIE-Datacom课程介绍
厦门微思网络HCIE-Datacom课程介绍 一、认证简介 HCIE-Datacom(Huawei Certified ICT Expert-Datacom)认证是华为认证体系中的顶级认证,HCIE-Datacom认证定位具备坚实的企业网络跨场景融合解决方案理论知识,能够使用华为数通产品…...
-QTableWight添加行和删除空行)
QT(C++)-QTableWight添加行和删除空行
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 1、前言2、QTableWidget的添加行3、删除行 1、前言 最近要用QT开发项目,对QT不是很熟,就根据网上的查到的知识和自己的摸索,将一…...

软件测试/测试开发丨Python 面向对象编程思想
面向对象是什么 Python 是一门面向对象的语言面向对象编程(OOP):Object Oriented Programming 所谓的面向对象,就是在编程的时候尽可能的去模拟真实的现实世界,按照现实世界中的逻辑去处理问题,分析问题中…...

一次降低进程IO延迟的性能优化实践——基于block层bfq调度器
如果有个进程正频繁的读写文件,此时你vim查看一个新文件,将会出现明显卡顿。即便你vim查看的文件只有几十M,也可能会出现卡顿。相对的,线上经常遇到IO敏感进程偶发IO超时问题。这些进程一次读写的文件数据量很少,正常几…...

C语言易错知识点十(指针(the final))
❀❀❀ 文章由不准备秃的大伟原创 ❀❀❀ ♪♪♪ 若有转载,请联系博主哦~ ♪♪♪ ❤❤❤ 致力学好编程的宝藏博主,代码兴国!❤❤❤ 许久不见,甚是想念,真的是时间时间,你慢些吧,不能再让头发变秃…...

React 18 新增的钩子函数
React 18 引入了一些新的钩子函数,用于处理一些常见的场景和问题。以下是 React 18 中引入的一些新钩子函数以及它们的代码示例和使用场景: useTransition: 代码示例:import { useTransition } from react;function MyComponent()…...
安装与部署Hadoop
一、前置安装准备1、机器2、java3、创建hadoop用户 二、安装Hadoop三、环境配置1、workers2、hadoop-env.sh3、core-site.xml4、hdfs-site.xml5、linux中Hadoop环境变量 四、启动hadoop五、验证 一、前置安装准备 1、机器 主机名ip服务node1192.168.233.100NameNode、DataNod…...
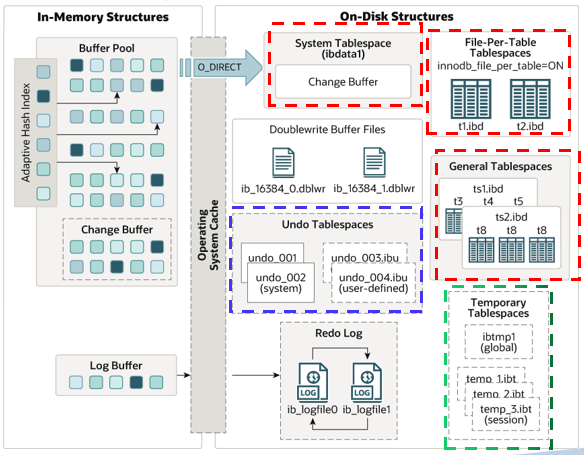
MySQL 8.0 InnoDB Tablespaces之General Tablespaces(通用表空间/一般表空间)
文章目录 MySQL 8.0 InnoDB Tablespaces之General Tablespaces(通用表空间/一般表空间)General tablespaces(通用表空间/一般表空间)通用表空间的功能通用表空间的限制 创建通用表空间(一般表空间)创建语法…...

循环生成对抗网络(CycleGAN)
一、说明 循环生成对抗网络(CycleGAN)是一种训练深度卷积神经网络以执行图像到图像翻译任务的方法。网络使用不成对的数据集学习输入和输出图像之间的映射。 二、基本介绍 CycleGAN 是图像到图像的翻译模型,就像Pix2Pix一样。Pix2Pix模型面临…...

数组--53.最大子数组和/medium
53.最大子数组和 1、题目2、题目分析3、解题步骤4、复杂度最优解代码示例5、抽象与扩展 1、题目 给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。 子数组 是数组中的一个连…...

centos 编译安装 python 和 openssl
安装环境: centos 7.9 : python 3.10.5 和 openssl 3.0.12 centos 6.10 : python 3.10.5 和 openssl 1.1.1 两个环境都能安装成功,可以正常使用。 安装 openssl 下载地址 下载后解压,进入到解压目录 执行…...
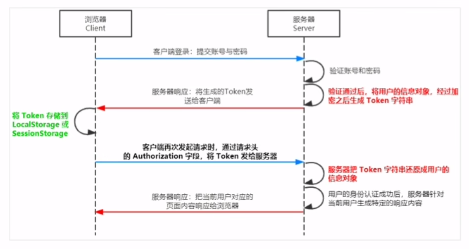
【nodejs】前后端身份认证
前后端身份认证 一、web开发模式 服务器渲染,前后端分离。 不同开发模式下的身份认证: 服务端渲染推荐使用Session认证机制前后端分离推荐使用JWT认证机制 二、session认证机制 1.HTTP协议的无状态性 了解HTTP协议的无状态性是进一步学习Session认…...

数据结构【线性表篇】(三)
数据结构【线性表篇】(三) 文章目录 数据结构【线性表篇】(三)前言为什么突然想学算法了?为什么选择码蹄集作为刷题软件? 目录一、双链表二、循环链表三、静态链表 结语 前言 为什么突然想学算法了? > 用较为“官方…...
Python装饰器的专业解释
装饰器,其实是用到了闭包的原理来进行操作的。 单个装饰器: 以下是一个简单的例子: def outer(func):print("OUTER enter ...")def wrapper(*args, **kwargs):print("调用之前......")result func(*args, **kwargs)p…...
vue3框架笔记
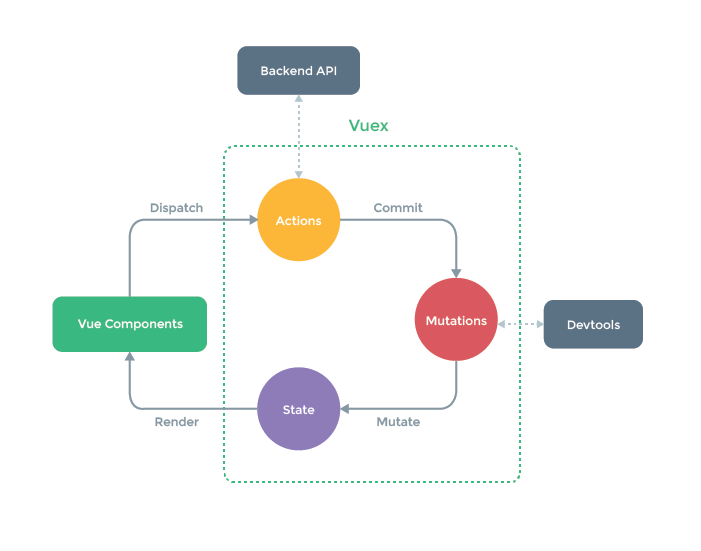
Vue Vue 是一个渐进式的前端开发框架,很容易上手。Vue 目前的版本是 3.x,但是公司中也有很多使用的是 Vue2。Vue3 的 API 可以向下兼容 2,Vue3 中新增了很多新的写法。我们课程主要以 Vue3 为主 官网 我们学习 Vue 需要转变思想࿰…...
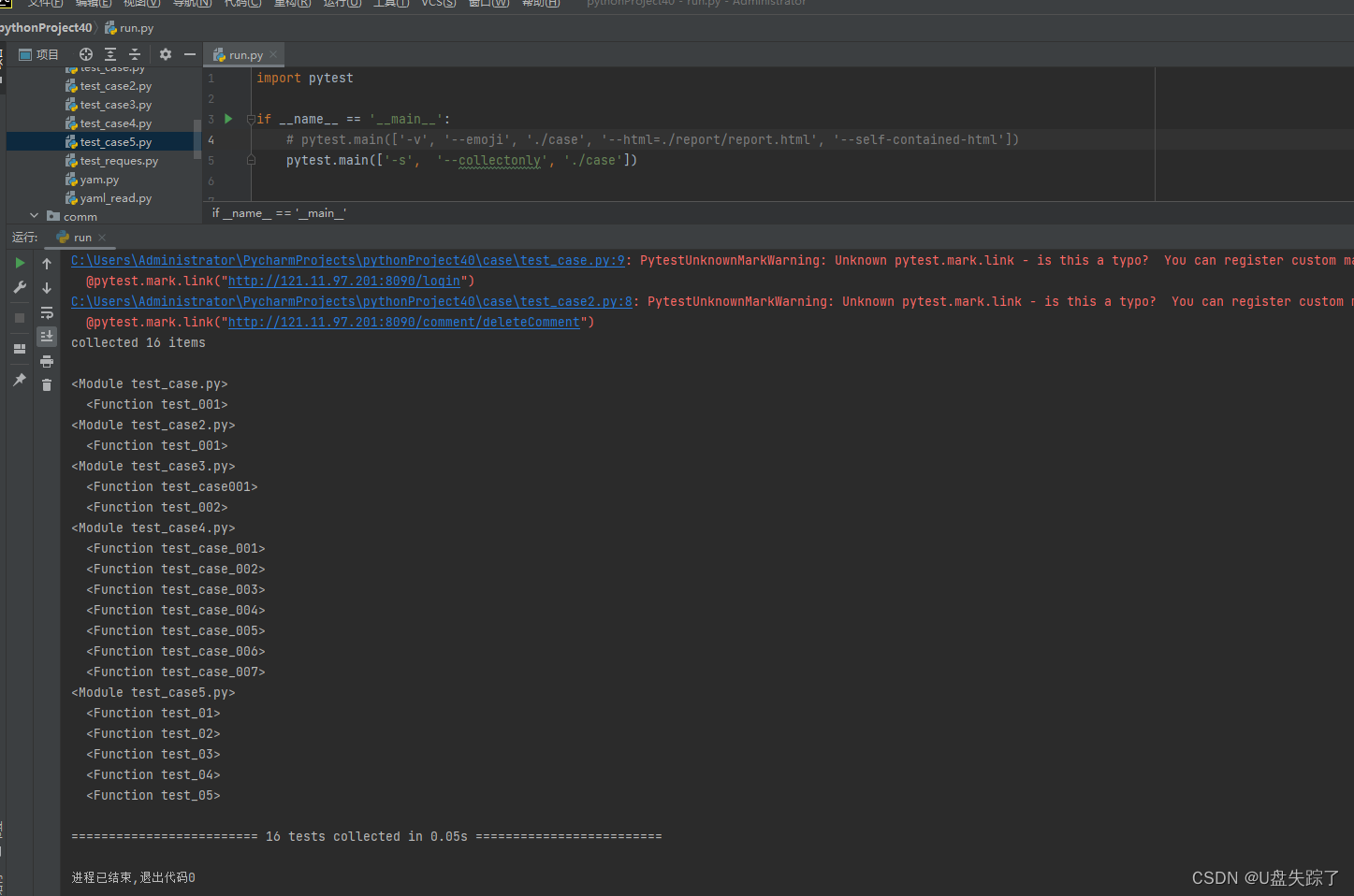
pytest --collectonly 收集测试案例
pytest --collectonly 是一条命令行指令,用于在运行 pytest 测试时仅收集测试项而不执行它们。它会显示出所有可用的测试项列表,包括测试模块、测试类和测试函数,但不会执行任何实际的测试代码。 这个命令对于查看项目中的测试结构和确保所有…...
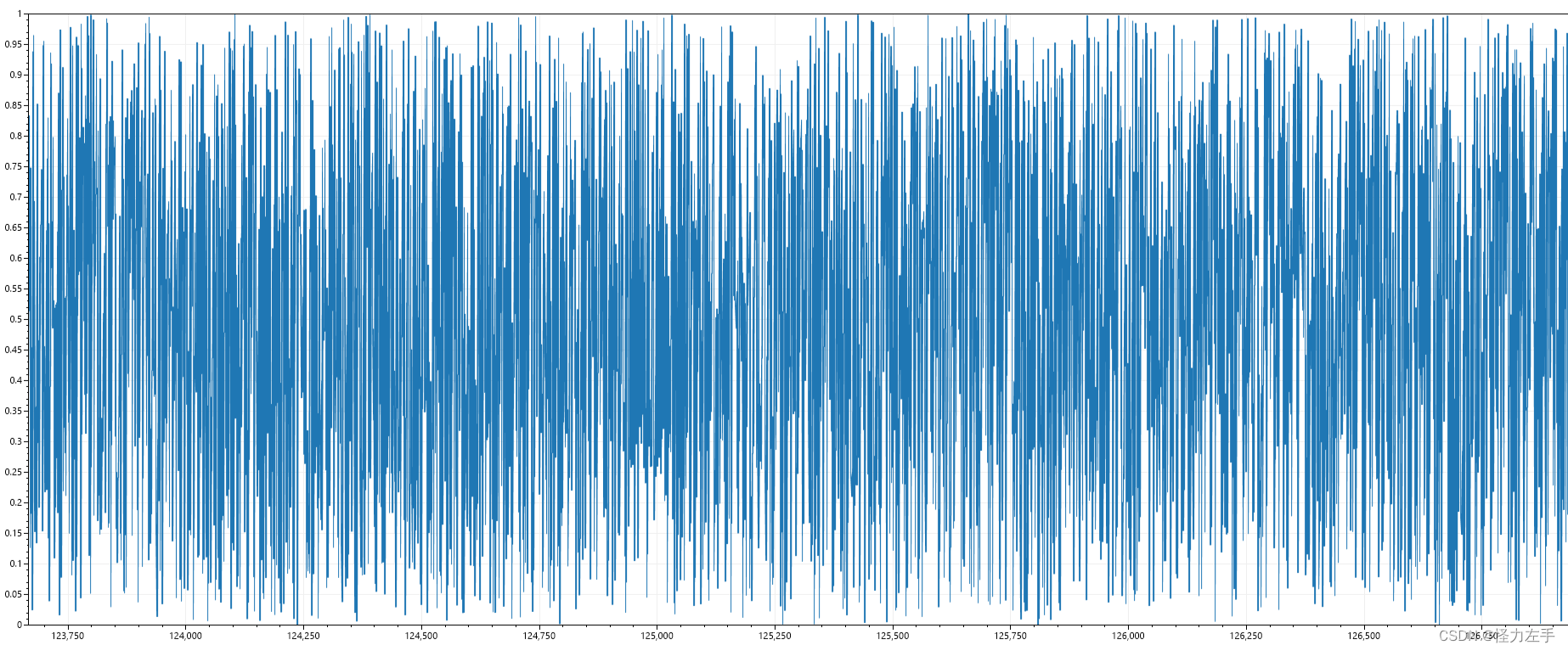
dev express 15.2图表绘制性能问题(dotnet绘图表)
dev express 15.2 绘制曲线 前端代码 <dxc:ChartControl Grid.Row"1"><dxc:XYDiagram2D EnableAxisXNavigation"True"><dxc:LineSeries2D x:Name"series" CrosshairLabelPattern"{}{A} : {V:F2}"/></dxc:XYDi…...

WorkPlus:领先的IM即时通讯软件,打造高效沟通协作新时代
在当今快节奏的商业环境中,高效沟通和协作是企业成功的关键。而IM即时通讯软件作为实现高效沟通的利器,成为了现代企业不可或缺的一部分。作为一款领先的IM即时通讯软件,WorkPlus以其卓越的性能和独特的功能,助力企业打造高效沟通…...
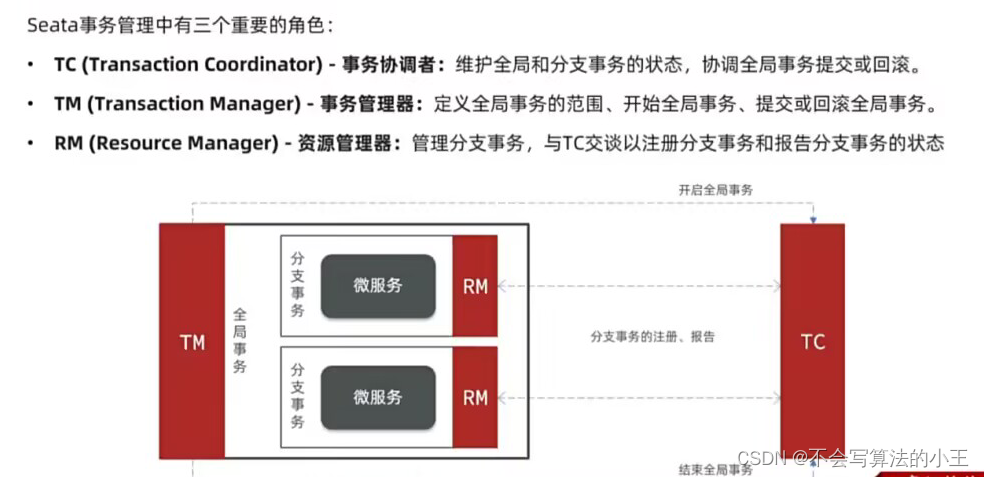
学习SpringCloud微服务
SpringCloud 微服务单体框架微服务框架SpringCloud微服务拆分微服务差分原则拆分商品服务拆分购物车服务拆分用户服务拆分交易服务拆分支付服务服务调用RestTemplate远程调用 微服务拆分总结 服务治理注册中心Nacos注册中心服务注册服务发现 OpenFeign实现远程调用快速入门引入…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...
