堆的应用:堆排序和TOP-K问题
上次才讲完堆的相关问题:二叉树顺序结构与堆的概念及性质(c语言实现堆
那今天就接着来进行堆的主要两方面的应用:堆排序和TOP-K问题
文章目录
- 1.堆排序
- 1.1概念、思路及代码
- 1.2改良代码(最初建立大堆用AdjustDow)
- 2. TOP-K问题
1.堆排序
1.1概念、思路及代码
堆排序即利用堆的思想来进行排序,总共分为两个步骤:
- 建立堆
- 升序:建立大堆
- 降序:建立小堆
- 利用堆删除思想来进行排序:堆顶元素是当前堆中的最大值(大堆)或最小值(小堆),将堆顶元素与堆中最后一个元素交换,然后将剩余元素重新调整成堆,再取出堆顶元素。重复上述步骤,直到所有元素都被取出,即完成了排序
#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}void AdjustUp(HPDataType* a, int child)
{int father = (child - 1) / 2;while (child > 0){if (a[child] > a[father]){Swap(&a[child], &a[father]);//更新下标child = father;father = (father - 1) / 2;}else{break;//一旦符合小堆了,就直接退出}}
}void AdjustDown(HPDataType* a, int n, int father)
{int child = father * 2 + 1;//假设左孩子大while (child < n){if (child + 1 < n && a[child] < a[child + 1]){child++;}if (a[child] > a[father]){Swap(&a[child], &a[father]);father = child;child = father * 2 + 1;}else{break;}}
}void HeapSort(int* arr, int n)//升序
{//先建大堆for (int i = 0; i < n; i++){AdjustUp(arr, i);}int a = n - 1;while (a > 0){//此时最大的是堆顶,堆顶跟最后一个交换Swap(&arr[0], &arr[a]);//现在最大的已经在最后了,不考虑它,把新塔顶降下来,重新编程大堆AdjustDown(arr, a, 0);a--;}}int main()
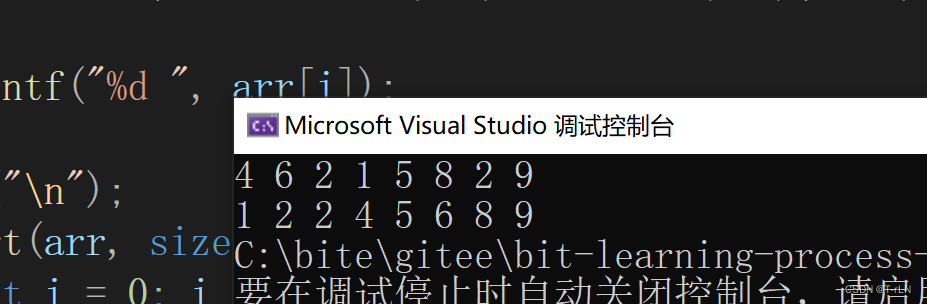
{int arr[]= { 4,6,2,1,5,8,2,9 };for (int i = 0; i < sizeof(arr) / sizeof(int); i++){printf("%d ", arr[i]);}printf("\n");HeapSort(arr, sizeof(arr) / sizeof(int));for (int i = 0; i < sizeof(arr) / sizeof(int); i++){printf("%d ", arr[i]);}
}
结果:
1.2改良代码(最初建立大堆用AdjustDow)
仅仅该那一部分:
void HeapSort(int* arr, int n)//升序
{//先建大堆//for (int i = 0; i < n; i++)//{// AdjustUp(arr, i);//}for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, n, i);}int a = n - 1;while (a > 0){//此时最大的是堆顶,堆顶跟最后一个交换Swap(&arr[0], &arr[a]);//现在最大的已经在最后了,不考虑它,把新塔顶降下来,重新编程大堆AdjustDown(arr, a, 0);a--;}}
对于一个具有n个节点的完全二叉树来说,最后一个非叶子节点的下标是(n-1-1)/2,也就是说,从最后一个非叶子节点开始,依次向上调整每个节点,就可以建立一个大堆
相比于向上调整,向下调整的好处:时间复杂度低
- 向下调整的时间复杂度是O(n),而向上调整的时间复杂度是O(nlogn)
建堆的时间复杂度为 O(n),排序过程的时间复杂度为 O(n log n)(建堆的时间复杂度为 O(n),而对堆进行排序的过程中,需要进行 n-1 次堆调整操作,每次堆调整的时间复杂度为 O(log n)。因此,排序过程的时间复杂度为 O(n log n))
2. TOP-K问题
TOP-K问题:求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大
对于Top-K问题,能想到的最简单直接的方式就是排序,然后直接取。 但是:如果数据量非常大,排序就不 太可取了,最佳的方式就是用堆来解决,基本思路如下:
- 用数据集合中前K个元素来建堆
- 要找前k个最大的元素,则建小堆
- 要找前k个最小的元素,则建大堆
- 用剩余的元素依次与堆顶元素来比较,不满足则替换堆顶元素:
- 要找前k个最大的元素:但凡剩余的有比小堆堆顶大的就进入到堆里面,然后向下沉;如果建立大堆有可能一个都进不来。
- 找前k个最小的也同理
void CreateData()//用来创建有随机数的文件的进行检测
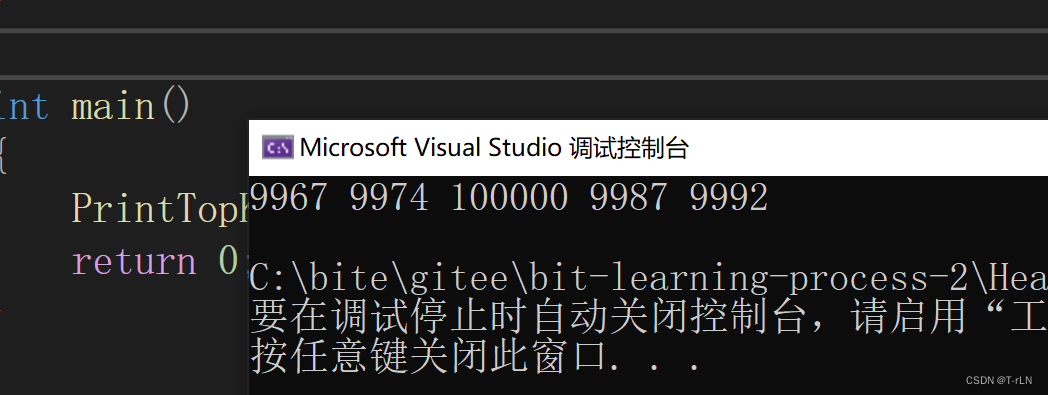
{int N = 1000;srand(time(0));FILE* f = fopen("data.txt", "w");for (int i = 0; i < N; i++){int a = (rand()) % 10000;fprintf(f,"%d\n", a);}fclose(f);}void PrintTopK(int k)//前k个大的
{//先读文件FILE* fout = fopen("data.txt", "r");if (fout == NULL){perror("fopen file");return -1;}int* a = (int*)malloc(sizeof(int) * k);for (int i = 0; i < k; i++)//建立元素k的小堆{fscanf(fout, "%d", &a[i]);//把文件里的前k个数字写入数组里AdjustUp(a, k);}//如果有比堆顶大的,就进来int n = 0;while (fscanf(fout, "%d", &n) != EOF)//读到文件读完就停止{if (n > a[0]){a[0] = n;AdjustDown(a, k, 0);}}for (int i = 0; i < k; i++){printf("%d ", a[i]);}printf("\n");fclose(fout);
}int main()
{PrintTopK(5);return 0;
}
结果如下:
那这次堆的两大应用就先到这里啦,到此二叉树顺序结构部分的知识也已经分享完毕了。感谢大家的支持,希望能帮助到大家!!!
相关文章:

堆的应用:堆排序和TOP-K问题
上次才讲完堆的相关问题:二叉树顺序结构与堆的概念及性质(c语言实现堆 那今天就接着来进行堆的主要两方面的应用:堆排序和TOP-K问题 文章目录 1.堆排序1.1概念、思路及代码1.2改良代码(最初建立大堆用AdjustDow) 2. TO…...
element表格排序功能
官方展示 个人项目 可以分别对每一项数据进行筛选 注:筛选的数据不能是字符串类型必须是数字类型,否则筛选会乱排序 html <el-table :data"tableData" border height"600" style"width: 100%"><el-table-co…...

HNU-Java程序设计基础训练-2023
1.DNA序列(Java) 【问题描述】 一个DNA序列由A/C/G/T四个字母的排列组合组成。G和C的比例(定义为GC-Ratio)是序列中G和C两个字母的总的出现次数除以总的字母数目(也就是序列长度)。在基因工程中…...

数据库和数据库编程
数据库、数据表、表数据操作以及数据库编程相关的知识点 1. 数据库的概念: 数据库是用于存储和组织数据的系统。数据库管理系统(DBMS)是管理数据库的软件,提供对数据的访问、查询和维护。关系型数据库是一种通过表格结构来组织和管理数据的数据库。 2…...
爬虫基础一(持续更新)
爬虫概念: 通过编写程序,模拟浏览器上网,然后让其去互联网上抓取数据的过程 分类: 1,通用爬虫:抓取一整张页面数据 2,聚焦爬虫:抓取页面中的局部内容 3,增量式爬虫&…...
右键菜单“以notepad++打开”,在windows文件管理器中
notepad 添加到文件管理器的右键菜单中 找到安装包,重新安装一般即可。 这里有最新版:地址 密码:f0f1 方法 在安装的时候勾选 “Context Menu Entry” 即可 Notepad的右击打开文件功能 默认已勾选 其作用是添加右键快捷键。即,对于任何…...

JSON.parseObject强制将自动转化的Intage型设置为Long型
通过Redis或Caffeine存储入json型String,通过JSON.parseObject自动类型转化之后,数值会优先转为Intage,如果存入的字符值大于Intage最大值,会自动转为Long型; 需求是:实要取出时数值类型值为Long࿱…...

Redis的集群模式:主从 哨兵 分片集群
基于Redis集群解决单机Redis存在的问题,在之前学Redis一直都是单节点部署 单机或单节点Redis存在的四大问题: 数据丢失问题:Redis是内存存储,服务重启可能会丢失数据 > 利用Redis数据持久化的功能将数据写入磁盘并发能力问题…...
Note: An Interesting Festival
An Interesting Festival 一个有趣的节日。 festival The Agricultural Feast takes place after the independence Day. 农业盛会在独立日后举行 takes place independence feast agricultural It is not a worldwide celebration. 它不是一个全球的庆典。 worldwide ce…...
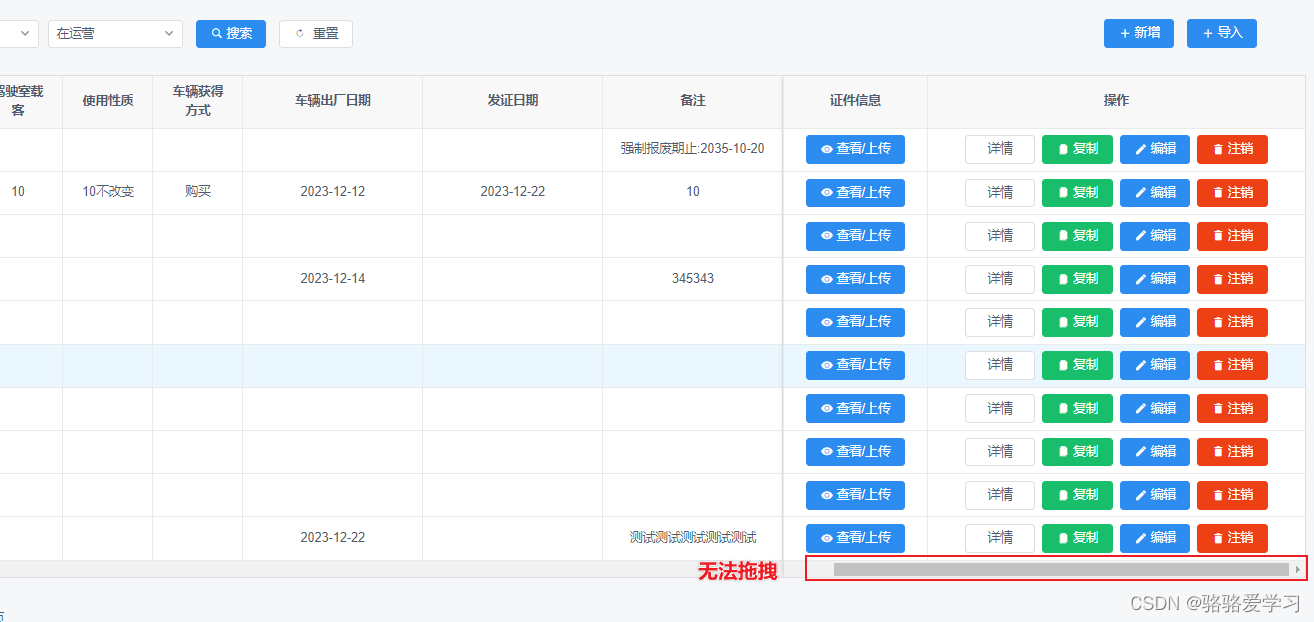
iview表格固定列横向滚动条无法拖动问题
文章目录 问题解决办法 问题 在使用iview的表格组件时,遇到了设置固定列表格后滚动条无法拖动的问题,当对表格列进行固定后,底部的横向滚动条就无法拖动了,主要的问题就是固定区域盖住了横向滚动条。 解决办法 在组件内直接加下…...

Python序列之集合
系列文章目录 Python序列之列表Python序列之元组Python序列之字典Python序列之集合(本篇文章) Python序列之集合 系列文章目录前言一、集合是什么?二、集合的操作1.集合的创建(1)使用{}创建(2)…...

智慧园区物联综合管理平台之架构简述
总体架构 系统总体划分为物联感知系统层、 核心平台层、 综合运营服务平台和展示层四部分。 物联感知系统层 物联感知系统主要是支撑园区智能化运行的各子系统, 包括门禁系统、 视频监控系统、 车辆管理系统等。 核心平台层 核心平台层包括: 园区物联综合管理平台和园区…...

国科大图像处理2023速通期末——汇总2017-2019
国科大2023.12.28图像处理0854期末重点 图像处理 王伟强 作业 课件 资料 一、填空 一个阴极射线管它的输入与输出满足 s r 2 sr^{2} sr2,这将使得显示系统产生比希望的效果更暗的图像,此时伽马校正通常在信号进入显示器前被进行预处理,令p…...
oracle 9i10g编程艺术-读书笔记2
配置Statspack 安装Statspack需要用internal身份登陆,或者拥有SYSDBA(connect / as sysdba)权限的用户登陆。需要在本地安装或者通过telnet登陆到服务器。 select instance_name,host_name,version,startup_time from v$instance;检查数据文件路径及磁盘空间&…...

PACC:数据中心网络的主动 CNP 生成方案
PACC:数据中心网络的主动 CNP 生成方案 文章目录 PACC:数据中心网络的主动 CNP 生成方案PACC算法CNP数据结构PACC参数仿真结果参考文献 PACC算法 CNP数据结构 PACC参数 仿真结果 PACC Hadoop Load0.2 的情况: PACC Hadoop Load0.4 的情况&a…...

我最喜欢的趣味几何书-读书笔记
我最喜欢的趣味几何书-读书笔记 1、利用阴影的长度来测量 公元前6世纪,古希腊哲学家泰勒思为了测量金字塔,想到了这样的方法:选择了一个特殊的时间,在那个时间,他自身的影子长度刚好跟他的身高相等。此时,…...
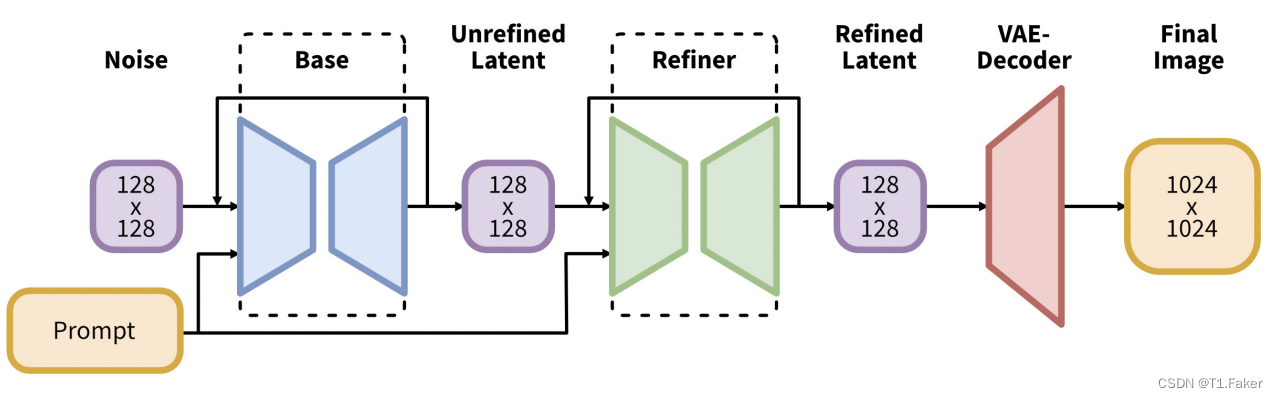
Stable Diffusion模型概述
Stable Diffusion 1. Stable Diffusion能做什么?2. 扩散模型2.1 正向扩散2.2 反向扩散 3. 训练如何进行3.1 反向扩散3.2 Stable Diffusion模型3.3 潜在扩散模型3.4 变分自动编码器3.5 图像分辨率3.6 图像放大 4. 为什么潜在空间是可能的?4.1 在潜在空间中…...

二叉树详解(深度优先遍历、前序,中序,后序、广度优先遍历、二叉树所有节点的个数、叶节点的个数)
目录 一、树概念及结构(了解) 1.1树的概念 1.2树的表示 二、二叉树概念及结构 2.1概念 2.2现实中的二叉树: 2.3数据结构中的二叉树: 2.4特殊的二叉树: 2.5 二叉树的存储结构 2.51 顺序存储: 2.5.2 链式存储&…...
C++日期类的实现
前言:在类和对象比较熟悉的情况下,我们我们就可以开始制作日期表了,实现日期类所包含的知识点有构造函数,析构函数,函数重载,拷贝构造函数,运算符重载,const成员函数 1.日期类的加减…...

B+树的插入删除
操作 插入 case2的原理,非叶子节点永远和最右边的最左边的节点的值相等。 case3:的基本原理 非叶子节点都是索引节点 底层的数据分裂之后 相当于向上方插入一个新的索引(你可以认为非叶子节点都是索引),反正第二层插入160 都要分裂,然后也需要再插入(因为索引部分不需要重…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...
