Unity中Shader裁剪空间推导(透视相机到裁剪空间的转化矩阵)
文章目录
- 前言
- 一、简单看一下 观察空间—>裁剪空间—>屏幕空间 的转化
- 1、观察空间(右手坐标系、透视相机)
- 2、裁剪空间(左手坐标系、且转化为了齐次坐标)
- 3、屏幕空间(把裁剪坐标归一化设置)
- 4、从观察空间到裁剪空间
- 5、从裁剪空间到屏幕空间后
- 二、透视相机的参数推导
- 1、从XoY平面,求出X~v~从观察空间到裁剪空间的坐标投影 X~p~
- 2、从YoZ平面,求出Y~v~从观察空间到裁剪空间的坐标投影 Y~p~
- 三、把投影到近裁剪面的坐标 归一化设置
- 1、求归一化设置后的 x~n~
- 2、求归一化设置后的 y~n~
- 3、得到最后化简的公式
- 四、构建转化矩阵
- 1、在OpenGL[-1,1]下:
- 2、在DirectX[1,0]下:
- 3、把A、B代入矩阵得
前言
我们把顶点坐标信息转化为裁剪空间。有可能使用到正交相机信息 或 透视相机。我们在这篇文章中,推导一下透视相机视图空间下的坐标转化到裁剪空间的矩阵。

一、简单看一下 观察空间—>裁剪空间—>屏幕空间 的转化

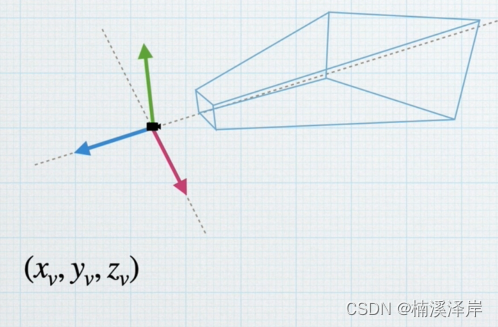
1、观察空间(右手坐标系、透视相机)
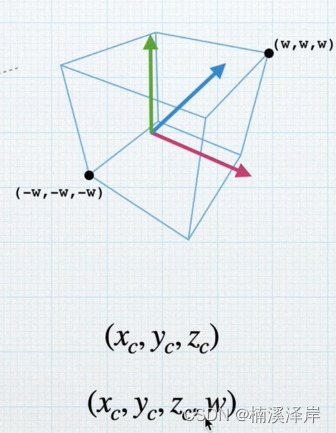
2、裁剪空间(左手坐标系、且转化为了齐次坐标)
3、屏幕空间(把裁剪坐标归一化设置)

4、从观察空间到裁剪空间
用透视投影矩阵先转化到裁剪空间
然后,在转化为齐次坐标
5、从裁剪空间到屏幕空间后
− 1 ≤ x c w ≤ 1 -1 \leq \frac{x_c}{w}\leq1 −1≤wxc≤1
− w ≤ x c ≤ w -w \leq x_c\leq w −w≤xc≤w
二、透视相机的参数推导
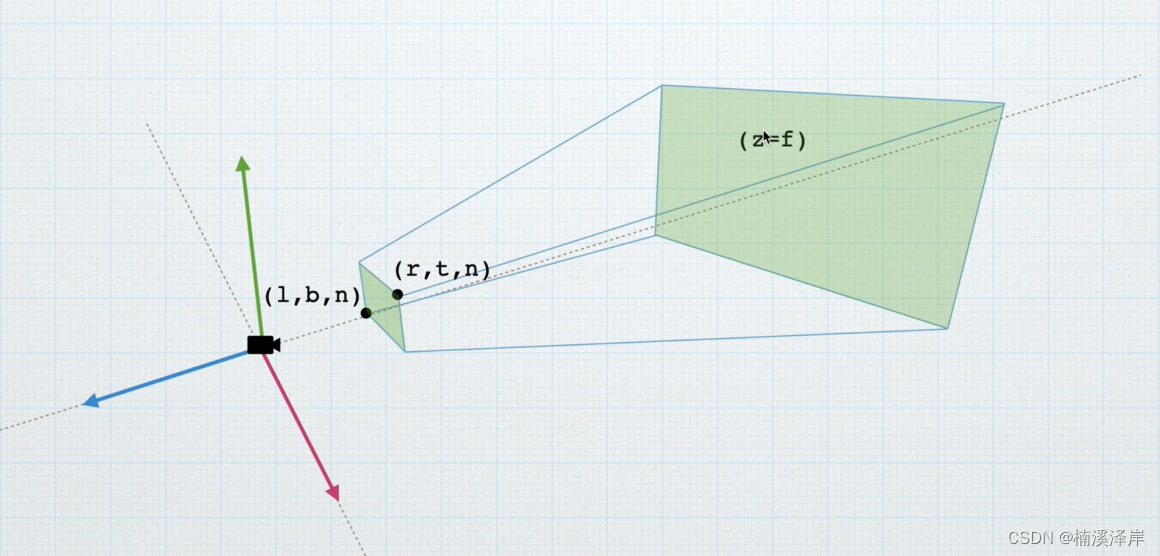
- 我们对于远裁剪面只是已知 f,其他参数都是未知
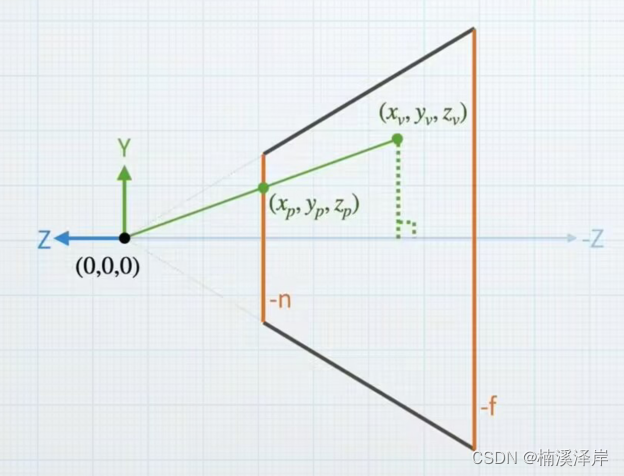
1、从XoY平面,求出Xv从观察空间到裁剪空间的坐标投影 Xp

- 点 V 是观察空间下的模型顶点,xyz是已知的
已知: ( x v , y v , z v ) 、 − n (x_v,y_v,z_v) 、 -n (xv,yv,zv)、−n - 点P是该点在近裁剪面上的投影点,xyz是未知的
未知: ( x p , y p , z p ) (x_p,y_p,z_p) (xp,yp,zp) - 我们在 XoZ平面上,能求的就是 xp
求: x p x_p xp
z p = − n z_p = -n zp=−n
y p 在 X o Z 平面下,无法计算 y_p 在XoZ平面下,无法计算 yp在XoZ平面下,无法计算
- v点向Z轴做垂线,原点连接v点,围成的两个三角形相似,可得:
x p x v = − n z v \frac{x_p}{x_v} = \frac{-n}{z_v} xvxp=zv−n
x p = − n z v x v x_p = \frac{-n}{z_v} x_v xp=zv−nxv
P = ( − n z v x v , 未知 , − n ) P = (\frac{-n}{z_v}x_v,未知,-n) P=(zv−nxv,未知,−n)
2、从YoZ平面,求出Yv从观察空间到裁剪空间的坐标投影 Yp
- 点 V 是观察空间下的模型顶点,xyz是已知的
已知: ( x v , y v , z v ) 、 − n (x_v,y_v,z_v) 、 -n (xv,yv,zv)、−n - 点P是该点在近裁剪面上的投影点,xyz是未知的
未知: ( x p , y p , z p ) (x_p,y_p,z_p) (xp,yp,zp) - 我们在 YoZ平面上,能求的就是 yp
求: y p y_p yp
z p = − n z_p = -n zp=−n
x p 在 X o Z 平面下,无法计算 x_p 在XoZ平面下,无法计算 xp在XoZ平面下,无法计算
- v点向Z轴做垂线,原点连接v点,围成的两个三角形相似,可得:
y p y v = − n z v \frac{y_p}{y_v} = \frac{-n}{z_v} yvyp=zv−n
y p = − n z v y v y_p = \frac{-n}{z_v} y_v yp=zv−nyv
P = ( − n z v x v , − n z v y v , − n ) P = (\frac{-n}{z_v}x_v,\frac{-n}{z_v} y_v,-n) P=(zv−nxv,zv−nyv,−n)
三、把投影到近裁剪面的坐标 归一化设置
P = ( − n z v x v , − n z v y v , − n ) P = (\frac{-n}{z_v}x_v,\frac{-n}{z_v} y_v,-n) P=(zv−nxv,zv−nyv,−n)
化到[-1,1]之间
具体参考Unity中Shader裁剪空间推导(正交相机到裁剪空间的转化矩阵)
1、求归一化设置后的 xn
- l ≤ x ≤ r l \leq x \leq r l≤x≤r 化为: − 1 ≤ 2 x w ≤ 1 -1 \leq \frac{2x}{w} \leq 1 −1≤w2x≤1
− 1 ≤ − 2 n x v z v w ≤ 1 -1\leq \frac{-2nx_v}{z_vw}\leq 1 −1≤zvw−2nxv≤1
− 1 ≤ − 2 n w ⋅ x v z v ≤ 1 -1\leq \frac{-2n}{w}·\frac{x_v}{z_v}\leq 1 −1≤w−2n⋅zvxv≤1
2、求归一化设置后的 yn
- l ≤ y ≤ r l \leq y \leq r l≤y≤r 化为: − 1 ≤ 2 y h ≤ 1 -1 \leq \frac{2y}{h} \leq 1 −1≤h2y≤1
− 1 ≤ − 2 n y v z v h ≤ 1 -1\leq\frac{-2ny_v}{z_vh}\leq1 −1≤zvh−2nyv≤1
− 1 ≤ − 2 n h ⋅ y v z v ≤ 1 -1\leq\frac{-2n}{h}·\frac{y_v}{z_v}\leq1 −1≤h−2n⋅zvyv≤1
3、得到最后化简的公式
由于NDC下的坐标由透视除法而得
我们假设透视除法中的 w 为 -zv
还原到裁剪空间还需要乘以 -zv
- X:
− 1 ≤ − 2 n w ⋅ x v z v ≤ 1 -1\leq \frac{-2n}{w}·\frac{x_v}{z_v}\leq 1 −1≤w−2n⋅zvxv≤1
x n = − 2 n w x v z v x_n = \frac{-2n}{w}\frac{x_v}{z_v} xn=w−2nzvxv
− x n z v = 2 n w x v -x_nz_v = \frac{2n}{w}x_v −xnzv=w2nxv
- Y:
− 1 ≤ − 2 n h ⋅ y v z v ≤ 1 -1\leq\frac{-2n}{h}·\frac{y_v}{z_v}\leq1 −1≤h−2n⋅zvyv≤1
y n = − 2 n h y v z v y_n = \frac{-2n}{h}\frac{y_v}{z_v} yn=h−2nzvyv
− y n z v = 2 n h y v -y_n z_v= \frac{2n}{h}y_v −ynzv=h2nyv
- Z:
z n = ? z_n = ? zn=?
− z n z v = − z v ? -z_nz_v = -z_v? −znzv=−zv?
- W:
w = 1 w = 1 w=1
− w n z v = − z v -w_nz_v = -z_v −wnzv=−zv
四、构建转化矩阵
裁剪空间下的点 = 观察空间下的基向量 在 裁剪空间下的矩阵 * 点在观察空间下的坐标
P c = [ V c ] ⋅ P v P_c = [V_c]·P_v Pc=[Vc]⋅Pv
P c = [ C v ] − 1 ⋅ P v P_c = [C_v]^{-1}·P_v Pc=[Cv]−1⋅Pv
P c = [ C v ] T ⋅ P v P_c = [C_v]^{T}·P_v Pc=[Cv]T⋅Pv
- − x n z v = 2 n w x v -x_nz_v = \frac{2n}{w}x_v −xnzv=w2nxv
- − y n z v = 2 n h y v -y_n z_v= \frac{2n}{h}y_v −ynzv=h2nyv
- − z n z v = − z v ? -z_nz_v = -z_v? −znzv=−zv?
- − w n z v = − z v -w_nz_v = -z_v −wnzv=−zv
[ 2 v w 0 ? ? 0 2 n h ? ? 0 0 ? ? 0 0 ? ? ] T = [ 2 v w 0 0 0 0 2 n h 0 0 ? ? ? ? ? ? ? ? ] \begin{bmatrix} \frac{2v}{w} & 0 & ? &?\\ 0 & \frac{2n}{h} & ? &?\\ 0 & 0 & ? &?\\ 0 & 0 & ? & ?\\ \end{bmatrix}^T =\begin{bmatrix} \frac{2v}{w} & 0 & 0 & 0 \\ 0 & \frac{2n}{h} & 0 &0\\ ? & ? & ? &?\\ ? & ? & ? & ?\\ \end{bmatrix} w2v0000h2n00???????? T= w2v0??0h2n??00??00??
[ 2 v w 0 0 0 0 2 n h 0 0 ? ? ? ? ? ? ? ? ] ⋅ [ x v y v z v 1 ] = ( − x n z v , − y n z v , − z n z v , − w n z v ) \begin{bmatrix} \frac{2v}{w} & 0 & 0 & 0 \\ 0 & \frac{2n}{h} & 0 &0\\ ? & ? & ? &?\\ ? & ? & ? & ?\\ \end{bmatrix} · \begin{bmatrix} x_v\\ y_v\\ z_v\\ 1\\ \end{bmatrix} = (-x_nz_v,-y_nz_v,-z_nz_v,-w_nz_v) w2v0??0h2n??00??00?? ⋅ xvyvzv1 =(−xnzv,−ynzv,−znzv,−wnzv)
最后一行由于相乘结果为1可以得出,把最后未知部分设为A,B
[ 2 v w 0 0 0 0 2 n h 0 0 0 0 A B 0 0 − 1 0 ] ⋅ [ x v y v z v 1 ] \begin{bmatrix} \frac{2v}{w} & 0 & 0 & 0 \\ 0 & \frac{2n}{h} & 0 &0\\ 0 & 0 & A &B\\ 0 & 0 & -1 & 0\\ \end{bmatrix} · \begin{bmatrix} x_v\\ y_v\\ z_v\\ 1\\ \end{bmatrix} w2v0000h2n0000A−100B0 ⋅ xvyvzv1
z c = A z v + B z_c = Az_v+B zc=Azv+B
− z n z v = − z v -z_nz_v = -z_v −znzv=−zv
z c − z v = A z v + B − z v \frac{z_c}{-z_v} = \frac{Az_v+B}{-z_v} −zvzc=−zvAzv+B
z n = A z v + B − z v z_n = \frac{Az_v+B}{-z_v} zn=−zvAzv+B
1、在OpenGL[-1,1]下:
z n = A z v + B − z v z_n = \frac{Az_v+B}{-z_v} zn=−zvAzv+B
{ z v = − n , z n = − 1 z v = − f , z n = 1 \begin{cases} z_v = -n,z_n=-1 \\ z_v = -f,z_n = 1 \end{cases} {zv=−n,zn=−1zv=−f,zn=1
{ − 1 = − A n + B n 1 = − A f + B f \begin{cases} -1 = \frac{-An+B}{n}\\ 1 = \frac{-Af + B}{f} \end{cases} {−1=n−An+B1=f−Af+B
{ − n = − A n + B f = − A f + B \begin{cases} -n = -An+B\\ f = -Af + B \end{cases} {−n=−An+Bf=−Af+B
B = A n − n B = An - n B=An−n
f = − A f + A n − n f = -Af +An-n f=−Af+An−n
f + n = A ( n − f ) f + n= A(n-f) f+n=A(n−f)
A = n + f n − f A = \frac{n+f}{n-f} A=n−fn+f
B = n + f n − f n − n B = \frac{n+f}{n-f}n-n B=n−fn+fn−n
B = n 2 + f n n − f n 2 − n f n − f B = \frac{n^2 + fn}{n-f}\frac{n^2-nf}{n-f} B=n−fn2+fnn−fn2−nf
B = 2 n f n − f B = \frac{2nf}{n-f} B=n−f2nf
2、在DirectX[1,0]下:
z n = A z v + B − z v z_n = \frac{Az_v+B}{-z_v} zn=−zvAzv+B
{ z v = − n , z n = 1 z v = − f , z n = 0 \begin{cases} z_v = -n,z_n=1 \\ z_v = -f,z_n = 0 \end{cases} {zv=−n,zn=1zv=−f,zn=0
{ 1 = − A n + B n 0 = − A f + B f \begin{cases} 1 = \frac{-An+B}{n}\\ 0 = \frac{-Af+B}{f} \end{cases} {1=n−An+B0=f−Af+B
{ n = − A n + B 0 = − A f + B \begin{cases} n = -An+B\\ 0 = -Af+B \end{cases} {n=−An+B0=−Af+B
B = A f B = Af B=Af
n = − A n + A f n = -An+Af n=−An+Af
n = A ( f − n ) n = A(f-n) n=A(f−n)
A = n f − n A =\frac{n}{f-n} A=f−nn
B = n f f − n B = \frac{nf}{f-n} B=f−nnf
3、把A、B代入矩阵得
- OpenGL
[ 2 n w 0 0 0 0 2 n h 0 0 0 0 n + f n − f 2 n f n − f 0 0 − 1 0 ] \begin{bmatrix} \frac{2n}{w} & 0 & 0 & 0 \\ 0 & \frac{2n}{h} & 0 &0\\ 0 & 0 & \frac{n+f}{n-f} &\frac{2nf}{n-f}\\ 0 & 0 & -1 & 0\\ \end{bmatrix} w2n0000h2n0000n−fn+f−100n−f2nf0 - DirectX
[ 2 n w 0 0 0 0 2 n h 0 0 0 0 n f − n n f f − n 0 0 − 1 0 ] \begin{bmatrix} \frac{2n}{w} & 0 & 0 & 0 \\ 0 & \frac{2n}{h} & 0 &0\\ 0 & 0 & \frac{n}{f-n} &\frac{nf}{f-n}\\ 0 & 0 & -1 & 0\\ \end{bmatrix} w2n0000h2n0000f−nn−100f−nnf0
相关文章:

Unity中Shader裁剪空间推导(透视相机到裁剪空间的转化矩阵)
文章目录 前言一、简单看一下 观察空间—>裁剪空间—>屏幕空间 的转化1、观察空间(右手坐标系、透视相机)2、裁剪空间(左手坐标系、且转化为了齐次坐标)3、屏幕空间(把裁剪坐标归一化设置)4、从观察空…...

企业签名分发对移动应用开发者有什么影响
企业签名分发是移动应用开发者在应用程序发布前测试、内部分发和特定的受众群体分发等方面比较常用的一种工具。那对于应用商城分发有啥区别,下面简单的探讨一下。 独立分发能力 通过企业签名分发开发者可以自己决定应用程序的发布时间和方式,不用受应用…...
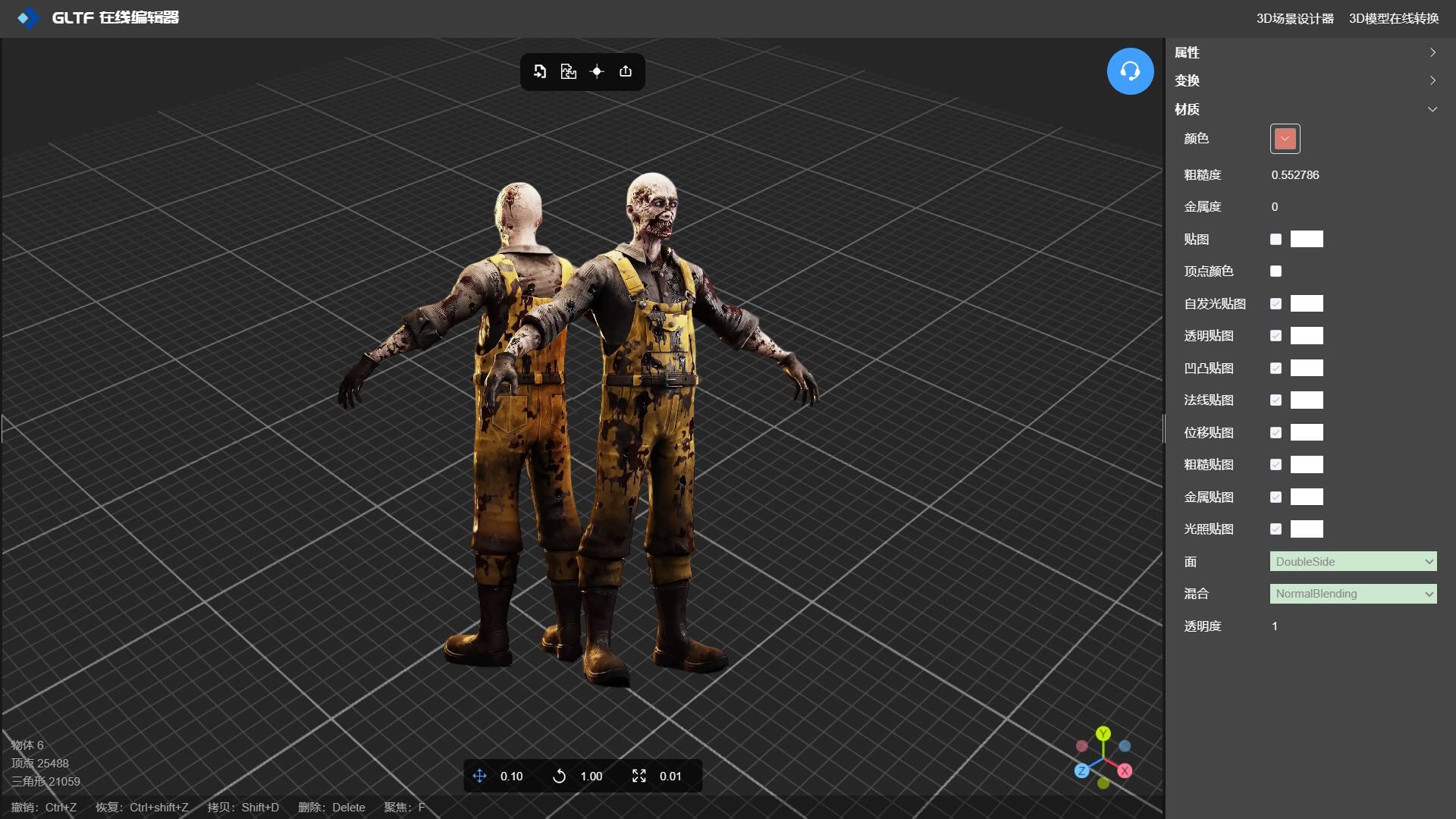
3D游戏角色建模纹理贴图处理
在线工具推荐: 3D数字孪生场景编辑器 - GLTF/GLB材质纹理编辑器 - 3D模型在线转换 - Three.js AI自动纹理开发包 - YOLO 虚幻合成数据生成器 - 三维模型预览图生成器 - 3D模型语义搜索引擎 在本文中,我们将介绍 3D 纹理的基础知识,并讨…...

【C++ 单例模式】
正确的析构 静态实例和回收类 SingletonMode.cpp #include <iostream> #include <pthread.h>class Singleton {private:Singleton(){std::cout << "构造" << std::endl;};~Singleton(){std::cout << "析构" << std::…...

React16源码: ConcurrentMode的使用及源码实现
ConcurrentMode 1 ) 概述 ConcurrentMode 是 React 16 出来的一个最令人振奋的功能在2018年年初是 Async Mode,在发布了16.6之后,名字进行了更新然后改成了 ConcurrentMode,中间的API有一个过渡的版本,后续会提到它其实是 React…...

SQL性能优化-索引
1.性能下降sql慢执行时间长等待时间长常见原因 1)索引失效 索引分为单索、复合索引。 四种创建索引方式 create index index_name on user (name); create index index_name_2 on user(id,name,email); 2)查询语句较烂 3)关联查询太多join&a…...

Ubuntu本地快速搭建web小游戏网站,公网用户远程访问
🔥博客主页: 小羊失眠啦. 🎥系列专栏:《C语言》 《数据结构》 《Linux》《Cpolar》 ❤️感谢大家点赞👍收藏⭐评论✍️ 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,…...
easyrecovery 2024最新免费密钥分享 实用数据恢复软件分享
在日常使用电脑时,我们经常会遇到误删文件的情况,若文件还未被彻底删除,我们还可以通过电脑中的回收站将其恢复,但若是回收站都被清空的话,想要恢复文件就变得比较困难了,而EasyRecovery可以很好的帮助我们…...

2.4信道复用技术
目录 2.4信道复用技术2.4.1频分复用、时分复用和统计时分复用频分复用FDM(Frequency Division Multiplexing)时分复用TDM(Time Division Multiplexing)统计时分复用STDM(Statistic TDM) 2.4.2波分复用2.4.3…...

JVM篇:JVM的简介
JVM简介 JVM全称为Java Virtual Machine,翻译过来就是java虚拟机,Java程序(Java二进制字节码)的运行环境 JVM的优点: Java最大的一个优点是,一次编写,到处运行。之所以能够实现这个功能就是依…...
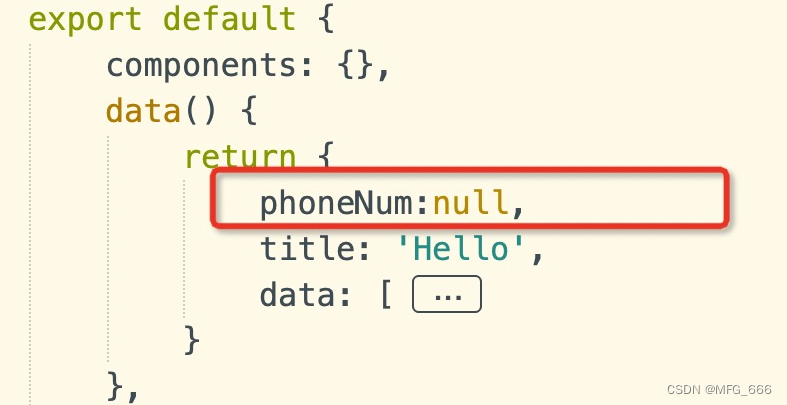
uniapp 输入手机号并且正则校验
1.<input input“onInput” :value“phoneNum” type“number” maxlength“11”/> 3. method里面写 onInput(e){ this.phoneNum e.detail.value }, 4.调用接口时候校验正则 if (!/^1[3456789]\d{9}$/.test(this.phoneNum)) {uni.showToast({title: 请输入正确的手机号…...

经典目标检测YOLO系列(一)复现YOLOV1(3)正样本的匹配及损失函数的实现
经典目标检测YOLO系列(一)复现YOLOV1(3)正样本的匹配及损失函数的实现 之前,我们依据《YOLO目标检测》(ISBN:9787115627094)一书,提出了新的YOLOV1架构,并解决前向推理过程中的两个问题,继续按照此书进行YOLOV1的复现。 经典目标…...
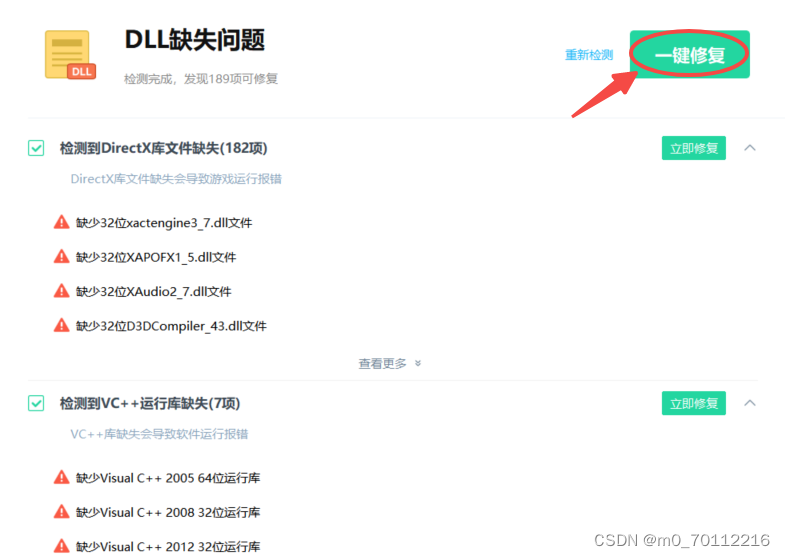
kbdnecat.DLL文件缺失,软件或游戏无法启动运营,快速修复方法
“kbdnecat.DLL文件是什么?为什么一起动游戏或软件,Windows就报错“kbdnecat.DLL文件缺失,软件无法启动””,应该怎么修复呢? 首先,先来了解“kbdnecat.DLL文件”是什么? kbdnecat.DLL是一个动…...
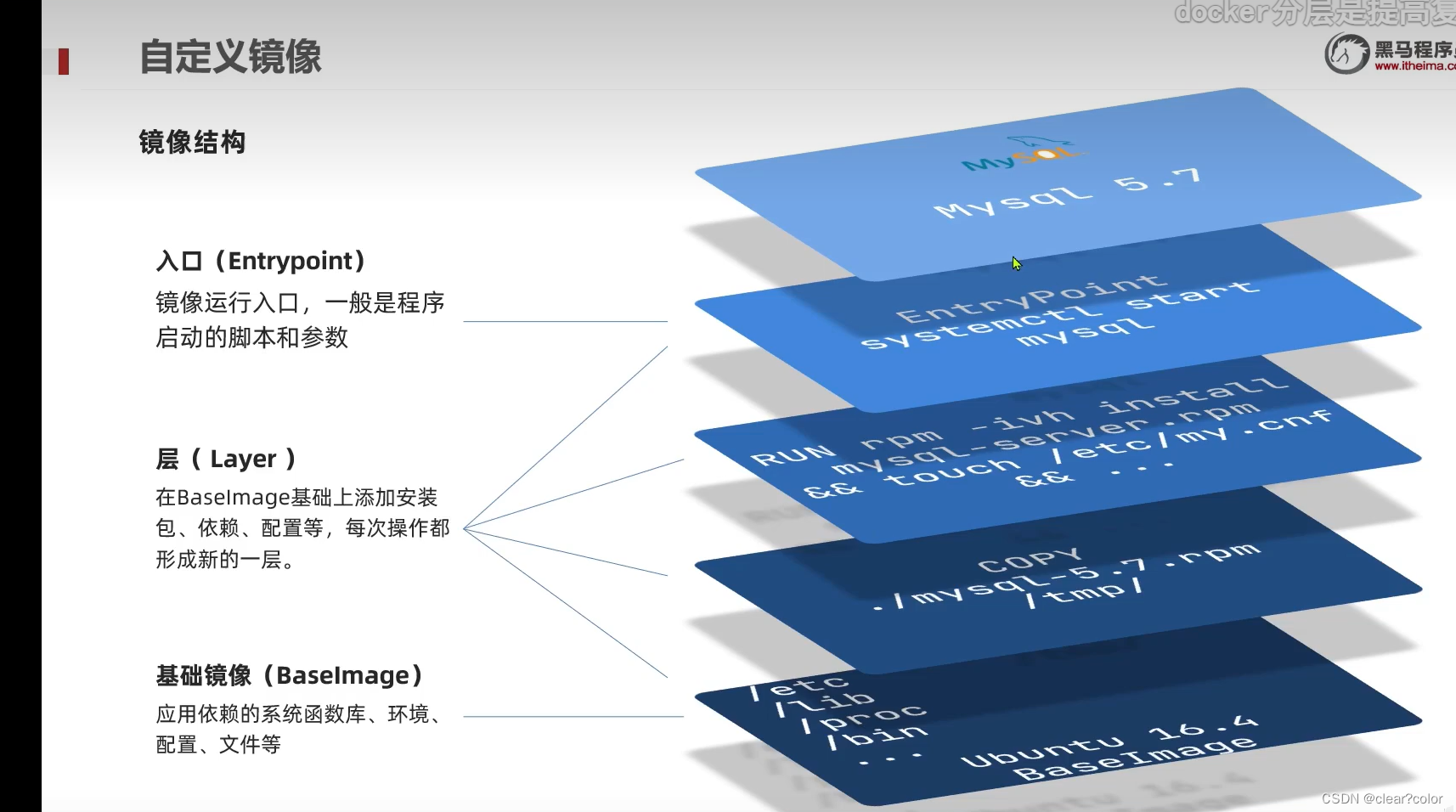
Dockerfile与DockerCompose
Docker的Image结构是怎样的? 镜像是将应用程序 及其需要的 系统函数库、环境、配置、依赖 打包而成。 镜像结构 入口( Entrypoint ) 镜像运行入口,一般是程序启动的脚本和参数 层( Layer ) 在BaseImage基…...
【CFP-专栏2】计算机类SCI优质期刊汇总(含IEEE/Top)
一、计算机区块链类SCI-IEEE 【期刊概况】IF:4.0-5.0, JCR2区,中科院2区; 【大类学科】计算机科学; 【检索情况】SCI在检; 【录用周期】3-5个月左右录用; 【截稿时间】12.31截稿; 【接收领域】区块链…...

Stable Diffusion 本地部署详细教程
目录 一、前言二、系统和硬件要求三、安装前说明四、安装步骤5、升级pip(这是管理python环境软件工具),并把资源库换成国内地址为清华镜像。一、前言 虽然MJ和SD都可以生成图像,但是为什么我们要考虑使用本地SD部署呢?原因其实很简单:首先,本地部署的使用成本更低,且更加…...
【超图】SuperMap iClient3D for WebGL/WebGPU —— 坐标系位置 —— Cartesian2
作者:taco 说到关于地理必然逃不开位置的关系。借用百度百科的内容来说地理学(geography),是研究地球表层空间地理要素或者地理综合体空间分布规律、时间演变过程和区域特征的一门学科。所以位置&坐标系必然逃不掉了。那么在S…...
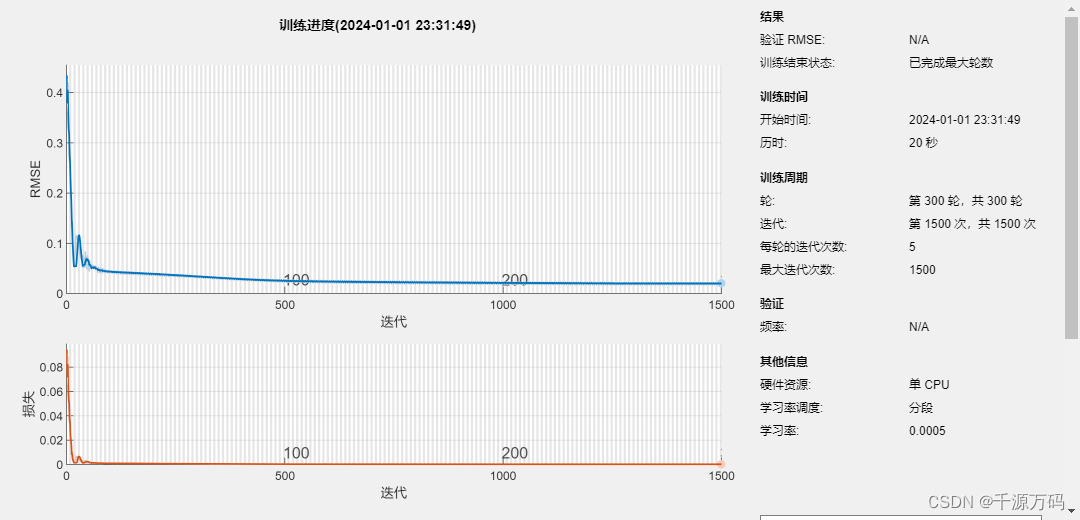
【Matlab】LSTM长短期记忆神经网络时序预测算法(附代码)
资源下载: https://download.csdn.net/download/vvoennvv/88688439 一,概述 LSTM(Long Short-Term Memory)是一种常用的循环神经网络(Recurrent Neural Network,RNN)结构,由于其对于…...

2.2 设计FMEA步骤二:结构分析
2.2.1 目的 设计结构分析的目的是将设计识别和分解为系统、子系统、组件和零件,以便进行技术风险分析。其主要目标包括: 可视化分析范围结构化表示:方块图、边界图、数字模型、实体零件识别设计接口、交互作用和间隙促进顾客和供应商工程团队之间的协作(接口责任)为功能分…...

红队攻防实战之DC2
吾愿效法古圣先贤,使成千上万的巧儿都能在21世纪的中华盛世里,丰衣足食,怡然自得 0x01 信息收集: 1.1 端口探测 使用nmap工具 可以发现开放了80端口,网页服务器但是可以看出做了域名解析,所以需要在本地完成本地域名…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...
