算法——队列+宽搜(BFS)
队列这种数据结构大都服务于一个算法——宽搜(BFS)。宽搜还可以运用到二叉树、图、迷宫最短路径问题、拓扑排序等等
N叉数的层序遍历
N叉树的层序遍历
题目解析
- 给定一个 N 叉树,返回其节点值的_层序遍历_。(即从左到右,逐层遍历)。
- 树的序列化输入是用层序遍历,每组子节点都由 null 值分隔(参见示例)。
算法原理
层序遍历(BFS宽度优先遍历):当我们遍历完 1、3、2、4时,要回过头看拓展3的子节点情况。这一过程属于先进先出的——队列这一数据结构可以解决,以二维数组的形式返回。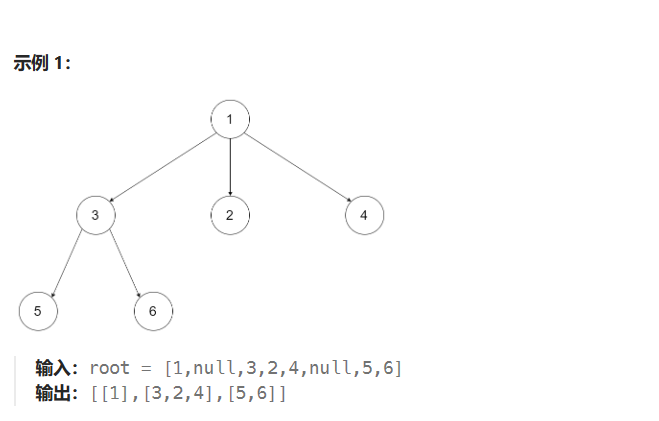
- 搞一个队列,如果根节点不为空,先让根节点入队。然后开始while循环,当队列不空的时候,把队头元素1拿出来,让队头元素的子节点2、3、4入队。接着继续将队头元素拿出来,让队头元素2的子节点5、6入队.接着将队头元素3拿出来,7入队,4拿出来,8入队。。继续拿出5、6、7、8(他们都没有子节点,就直接拿出即可)

· 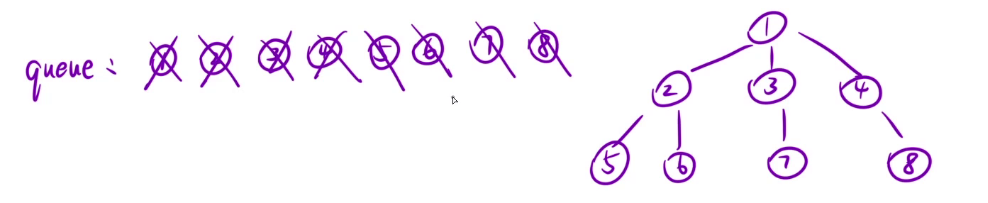
- 这里还有一个问题,在一次访问遍历节点时,如果出现不同层的节点元素进入,该怎样统计呢?我们这里只需要设置一个变量,统计元素个数。即当1进入队列时,计数为1;当1出队列时,2、3、4进入。此时个数为3就令变量为3。第二层出完时。第三层四个元素已经全部进入,令变量为4。
代码实现
/*
// Definition for a Node.
class Node {
public:int val;vector<Node*> children;Node() {}Node(int _val) {val = _val;}Node(int _val, vector<Node*> _children) {val = _val;children = _children;}
};
*/class Solution
{
public:vector<vector<int>> levelOrder(Node* root) {vector<vector<int>> ret; // 记录最终结果queue<Node*> q; // 层序遍历需要的队列if(root == nullptr) return ret;q.push(root);while(q.size()){int sz = q.size(); // 先求出本层元素的个数vector<int> tmp; // 统计本层的节点for(int i = 0; i < sz; i++){Node* t = q.front(); //拿出队头元素q.pop();tmp.push_back(t->val); //将节点加入到最终返回的数组中for(Node* child : t->children) // 遍历它的子节点,让下⼀层结点⼊队{if(child != nullptr)q.push(child);}}ret.push_back(tmp);}return ret;}
};
二叉树的锯齿形层序遍历
二叉树的锯齿形层序遍历
题目解析
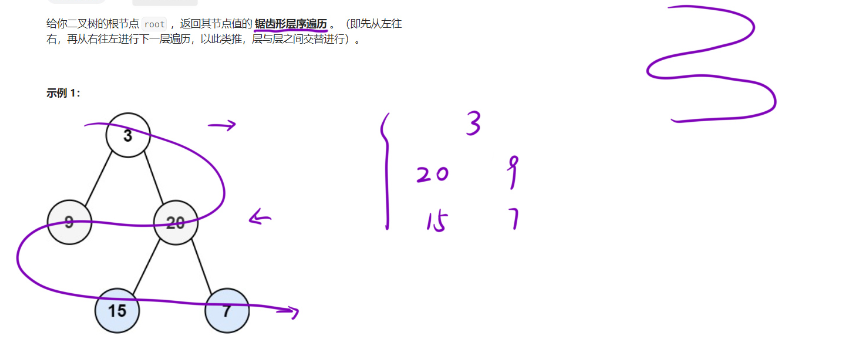
算法原理
解法:层序遍历
在层序遍历的结果存到最终返回结果之前,奇数行直接存入要返回的ret里,偶数行多执行一个逆序返回到ret里面即可。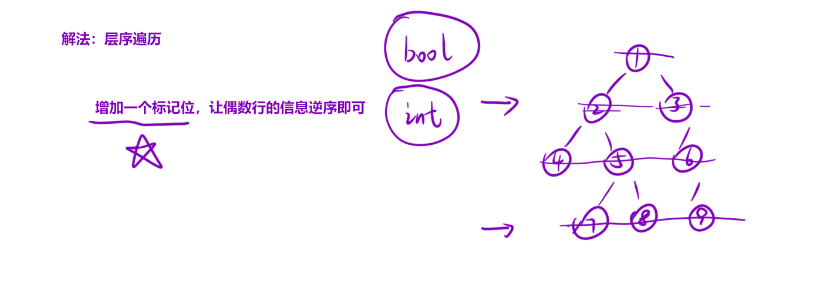
代码实现
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution
{
public:vector<vector<int>> zigzagLevelOrder(TreeNode* root) {vector<vector<int>> ret;if(root == nullptr) return ret;queue<TreeNode*> q;q.push(root);int level = 1;while(q.size()){int sz = q.size();vector<int> tmp;for(int i = 0; i < sz; i++){auto t = q.front();q.pop();tmp.push_back(t->val);if(t->left) q.push(t->left);if(t->right) q.push(t->right);}// 判断是否逆序if(level % 2 == 0) reverse(tmp.begin(), tmp.end());ret.push_back(tmp);level++;}return ret;}
};
二叉树最大宽度
二叉树最大宽度
题目解析
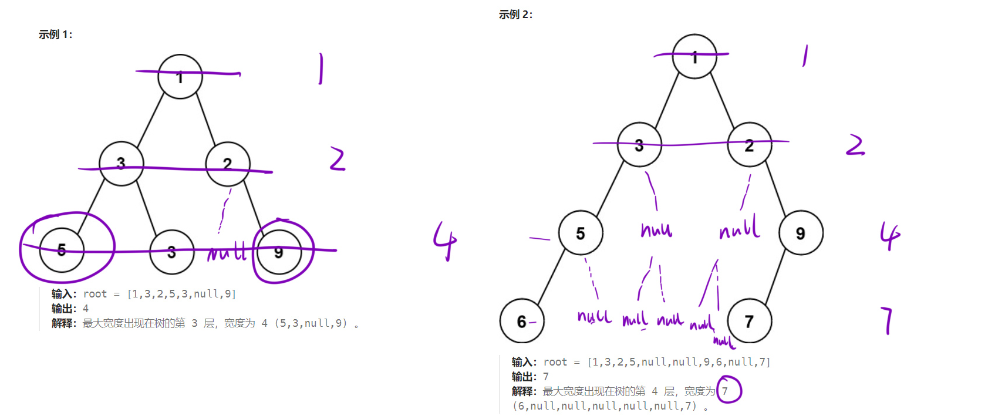
- 给你一棵二叉树的根节点 root ,返回树的 最大宽度 。
- 树的 最大宽度 是所有层中最大的 宽度 。
- 每一层的 宽度 被定义为该层最左和最右的非空节点(即,两个端点)之间的长度。将这个二叉树视作与满二叉树结构相同,两端点间会出现一些延伸到这一层的 null 节点,这些 null 节点也计入长度。
算法原理
解法一:硬来层序遍历
统计每⼀层的最⼤宽度,我们优先想到的就是利⽤层序遍历,把当前层的结点全部存在队列⾥⾯,利⽤队列的⻓度来计算每⼀层的宽度,统计出最⼤的宽度。但是,由于空节点也是需要计算在内的。因此,我们可以选择将空节点也存在队列⾥⾯。
当遍历到最后一层时,最后一层宽度为7。可以定义一个empty(统计null个数),从最后一层第一个位置开始扫描,遇到null节点+1,直至遇到下一个有效数字。停止,计算出宽度。然后再将empty置空为0,然后继续向后遍历,因为后面没有真实数字节点,所以最后一个null不计入宽度里。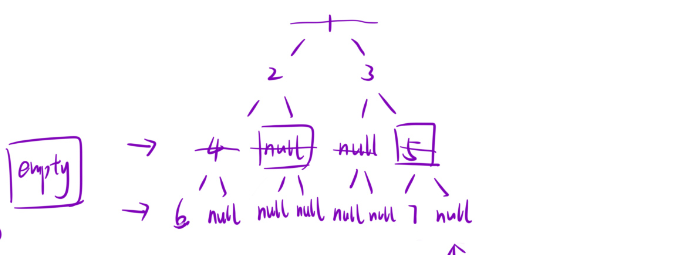
但是这里会超时,会有一种极端情况。将3000个节点平均分(题中给的数据范围为3000),如果还按照我们上述计算宽度的算法,那么最后一层将达到21000,这样是大大超出内存的。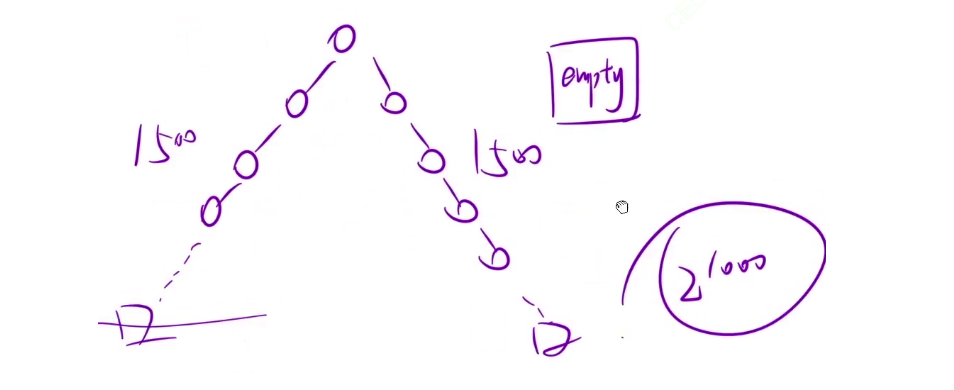
解法二:利用数组存储二叉树,给节点编号
树我们不仅有链式存储,还有顺序存储。我们可以通过给二叉树节点编号,通过公式计算给他的子节点编号(两个公式区别就是头结点从1开始计数还是从0开始计数)
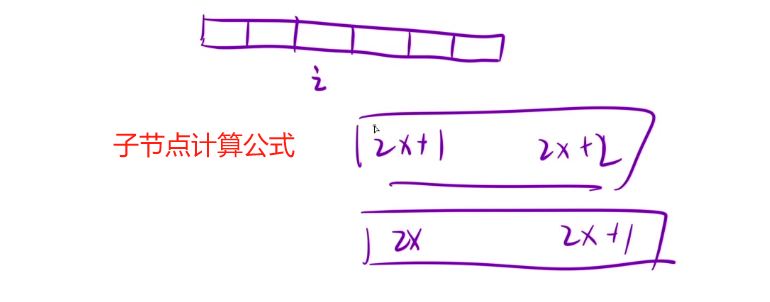
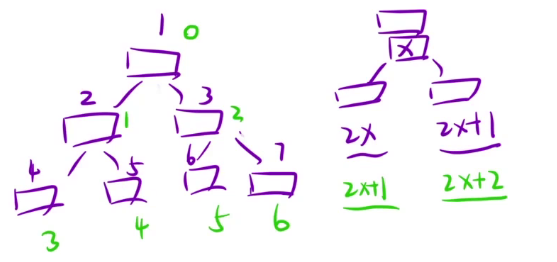
-
创建一个队列,此时队列里就不仅仅存储节点,我们即存他的节点,也存他的编号。计算宽度方法就是拿出这个队的队头,拿出这个队的对尾,下标相减+1即可;这样就不需要处理空节点了。(有的容器只能访问队头,不能访问队尾,这对于计算宽度就有些麻烦,我们可以用数组模拟队列)
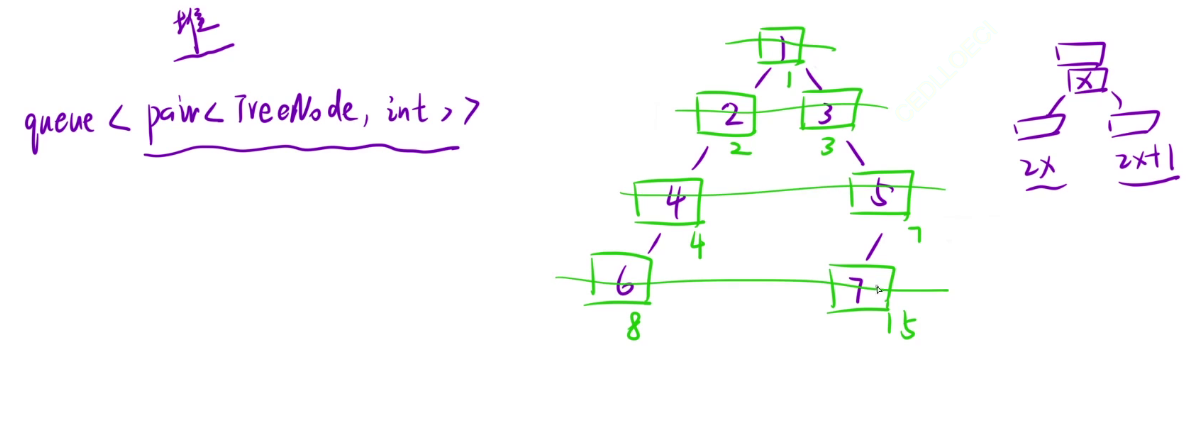
-
细节问题:下标有可能溢出。再次回到解法一遇到的极端情况,在那种情况下,最后一层的最后一个节点编号为21500-1.这个数字是任何一个数据类型都存不下的。但是当我们相减之后算出最后结果也是正确的。因为我们的数据存储是一个环形存储,我们最终计算的是距离(绿色部分),这个距离是不会溢出的,所以结果是正确的。我们C++用unsigned int存储就不会报错了
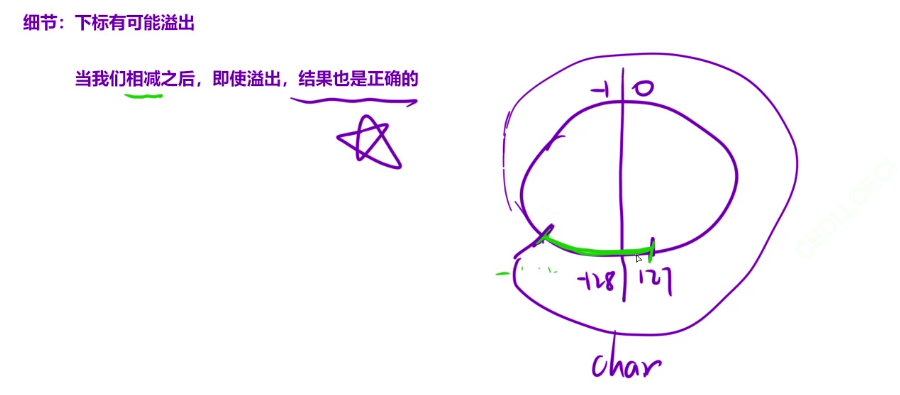
代码实现
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution
{
public:int widthOfBinaryTree(TreeNode* root) {vector<pair<TreeNode*, unsigned int>> q; // ⽤数组模拟队列q.push_back({root, 1});unsigned int ret = 0;while(q.size()){// 先更新这⼀层的宽度auto& [x1, y1] = q[0];auto& [x2, y2] = q.back();ret = max(ret, y2 - y1 + 1);// 让下⼀层进队vector<pair<TreeNode*, unsigned int>> tmp; // 让下⼀层进⼊这个队列for(auto& [x, y] : q){if(x->left) tmp.push_back({x->left, y * 2});if(x->right) tmp.push_back({x->right, y * 2 + 1});}q = tmp;}
return ret;}
};
在每个树行中找最大值
在每个树行中找最大值
题目解析
给定一棵二叉树的根节点 root ,请找出该二叉树中每一层的最大值。
算法原理
利用层序遍历,统计出每一层的最大值。
代码实现
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution
{
public:vector<int> largestValues(TreeNode* root) {vector<int> ret;if(root == nullptr) return ret;queue<TreeNode*> q;q.push(root);while(q.size()){int sz = q.size();int tmp = INT_MIN; //初始化为无穷小,让数字与tmp比较for(int i = 0; i < sz; i++){auto t = q.front(); //拿出队头元素q.pop(); //干掉队头元素tmp = max(tmp, t->val); //更新这一层最大值if(t->left) q.push(t->left); //让其子节点入队if(t->right) q.push(t->right);}ret.push_back(tmp);}return ret;}
};
相关文章:

算法——队列+宽搜(BFS)
队列这种数据结构大都服务于一个算法——宽搜(BFS)。宽搜还可以运用到二叉树、图、迷宫最短路径问题、拓扑排序等等 N叉数的层序遍历 N叉树的层序遍历 题目解析 给定一个 N 叉树,返回其节点值的_层序遍历_。(即从左到右&#…...
前端八股文(CSS篇)二
目录 1.css中可继承与不可继承属性有哪些 2.link和import的区别 3.transition和animation的区别 4.margin和padding的使用场景 5.::before和:after的双冒号和单冒号有什么区别? 6.display:inline-block什么时候会显示间隙 7…...
系统架构设计师笔记
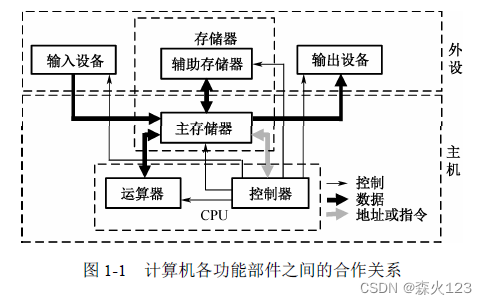
第1章计算机组成与体系结构 1.1.1计算机硬件的组成 (1)控制器。控制器是分析和执行指令的部件,也是统一指挥并控制计算机各部件协调工作的中心部件,所依据的是机器指令。控制器的组成包含如下。 ①程序计数器PC:存储下…...

Livox-Mid-360 固态激光雷达ROS格式数据分析
前言: Livox-Mid-360 官方采用livox_ros_driver2ROS功能包发布ROS格式的数据,livox_ros_driver2可以把Livox原始雷达数据转化成ROS格式并以话题的形式发布出去。 下面列举一些雷达的基本概念: 点云帧:雷达驱动每次向外发送的一…...

如何恢复 iPhone 上永久删除的照片?
2007年,苹果公司推出了一款惊天动地的智能手机,也就是后来的iPhone。你会惊讶地发现,迄今为止,苹果公司已经售出了 7 亿部 iPhone 设备。根据最新一项调查数据,智能手机利润的 95% 都进了苹果公司的腰包。 如此受欢迎…...

基于单片机的公交车站自动报站器设计与实现
一、摘要 随着城市交通的快速发展,公交车作为城市公共交通的主要工具,其便捷性和高效性得到了广泛的认可。然而,由于公交车站的广播系统存在一定的局限性,如人工报站容易出现失误、音量大小不一等问题,给乘客带来了不…...
python之Selenium WebDriver安装与使用
首先把python下载安装后,再添加到环境变量中,再打开控制台输入: pip install selenium 正常情况下是安装好的,检查一下“pip show selenium”命令,出现版本号就说明安装好了。 1:如果出现安装错误: 那就用“…...
基于Java+Vue+uniapp微信小程序国产动漫论坛系统设计和实现
博主介绍:✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和学生毕业项目实战,高校老师/讲师/同行交流合作✌ 主要内容:SpringBoot、Vue、SSM、HLM…...
)
奇因子之和(C语言)
题意: 一个整数的因子,就是所有可以整除这个数的数。奇数指在整数中,不能被 2 整除的数。所谓整数 Z 的奇因子,就是可以整除 Z 的奇数。 给定 N 个正整数,请你求出它们的第二大奇因子的和。当然,如果该数只…...

简单FTP客户端软件开发——VMware安装Linux虚拟机(命令行版)
VMware安装包和Linux系统镜像: 链接:https://pan.baidu.com/s/1UwF4DT8hNXp_cV0NpSfTww?pwdxnoh 提取码:xnoh 这个学期做计网课程设计【简单FTP客户端软件开发】需要在Linux上配置 ftp服务器,故此用VMware安装了Linux虚拟机&…...
ArkTS开发实践
声明式UI基本概念 应用界面是由一个个页面组成,ArkTS是由ArkUI框架提供,用于以声明式开发范式开发界面的语言。 声明式UI构建页面的过程,其实是组合组件的过程,声明式UI的思想,主要体现在两个方面: 描述…...

vue项目中实现预览pdf
vue项目中实现预览pdf 1. iframe <iframe :src"pdfSrc"></iframe> data() {return {pdfSrc: http://192.168.0.254:19000/trend/2023/12/27/5635529375174c7798b5fabc22cbec45.pdf,}},iframe {width: 100%;height: calc(100vh - 132px - 2 * 20px -…...
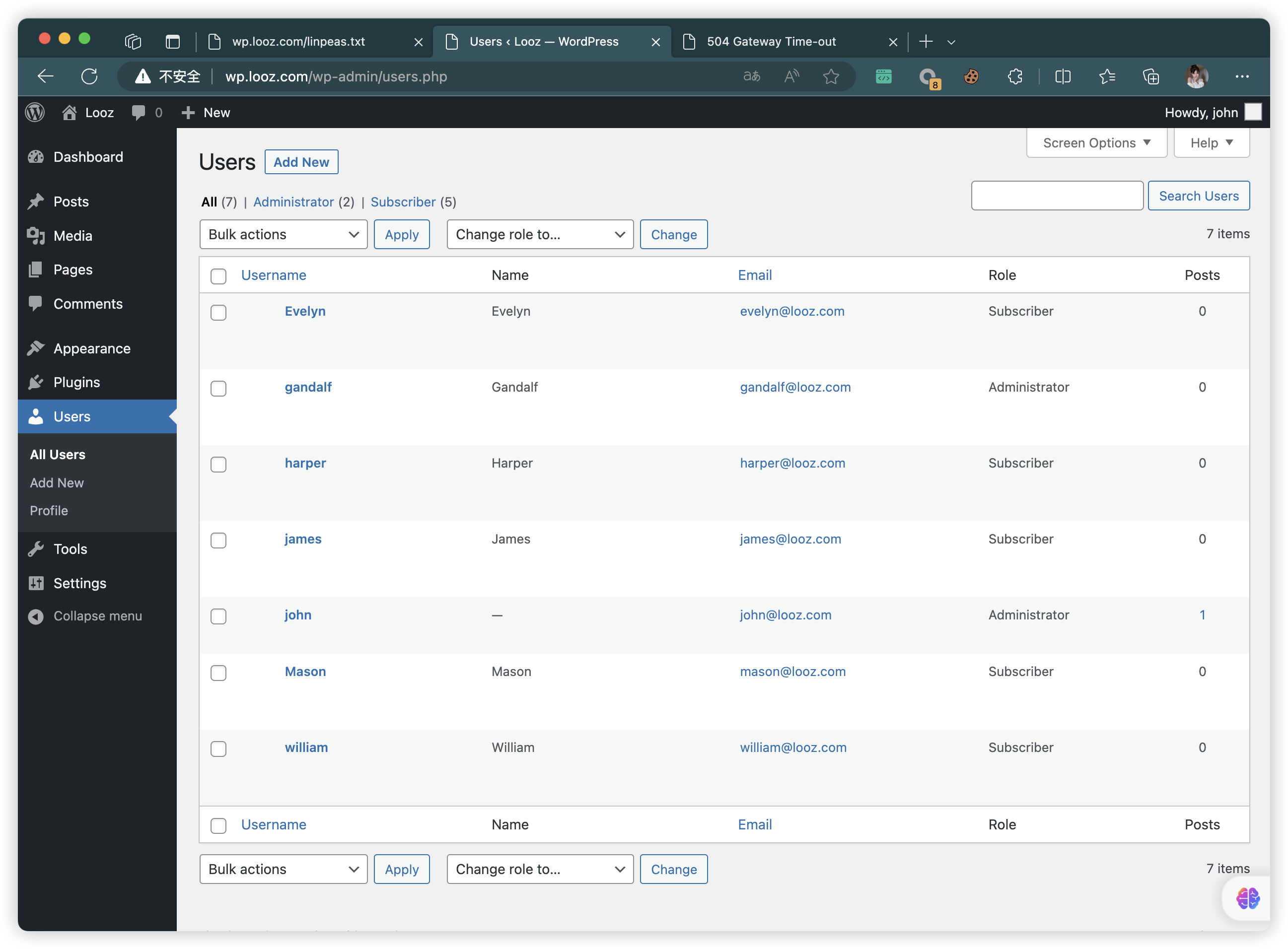
【Vulnhub 靶场】【Looz: 1】【简单】【20210802】
1、环境介绍 靶场介绍:https://www.vulnhub.com/entry/looz-1,732/ 靶场下载:https://download.vulnhub.com/looz/Looz.zip 靶场难度:简单 发布日期:2021年08月02日 文件大小:2.1 GB 靶场作者:mhz_cyber &…...

计算机基础面试题 |03.精选计算机基础面试题
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...

SQL最消耗性能查询错误用法示例
查询性能的消耗主要取决于查询的复杂度、表的大小以及使用的索引等因素。以下是一些查询中常见的错误用法示例,它们可能导致性能问题: 全表扫描: 错误用法示例: SELECT * FROM your_table;这种查询会检索表中的所有行,…...
面向对象编程)
Python学习笔记(六)面向对象编程
最近准备HCIE的考试,用空余时间高强度学习python 介绍了Python中面向对象编程的基本概念,包括类、类的属性、类的方法、类的方法中实例方法、类方法、静态方法,在类与对象中动态添加属性和方法,以及继承、类变量、多态等概念 类…...
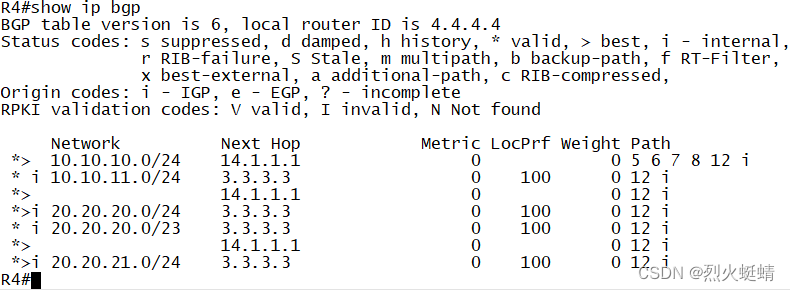
CCNP课程实验-05-Comprehensive_Experiment
目录 实验条件网络拓朴 基础配置实现IGP需求:1. 根据拓扑所示,配置OSPF和EIGRP2. 在R3上增加一个网段:33.33.33.0/24 (用Loopback 1模拟) 宣告进EIGRP,并在R3上将EIGRP重分布进OSPF。要求重分布进OSPF后的路由Tag值设置为666&…...

第3课 使用FFmpeg获取并播放音频流
本课对应源文件下载链接: https://download.csdn.net/download/XiBuQiuChong/88680079 FFmpeg作为一套庞大的音视频处理开源工具,其源码有太多值得研究的地方。但对于大多数初学者而言,如何快速利用相关的API写出自己想要的东西才是迫切需要…...

Java 动态树的实现思路分析
Java 动态树的实现 目录概述需求: 设计思路实现思路分析1. 简单Java实现:2.建立父子表存储3.前端的对应的json 字符串方式 参考资料和推荐阅读 Survive by day and develop by night. talk for import biz , show your perfect code,full busy࿰…...
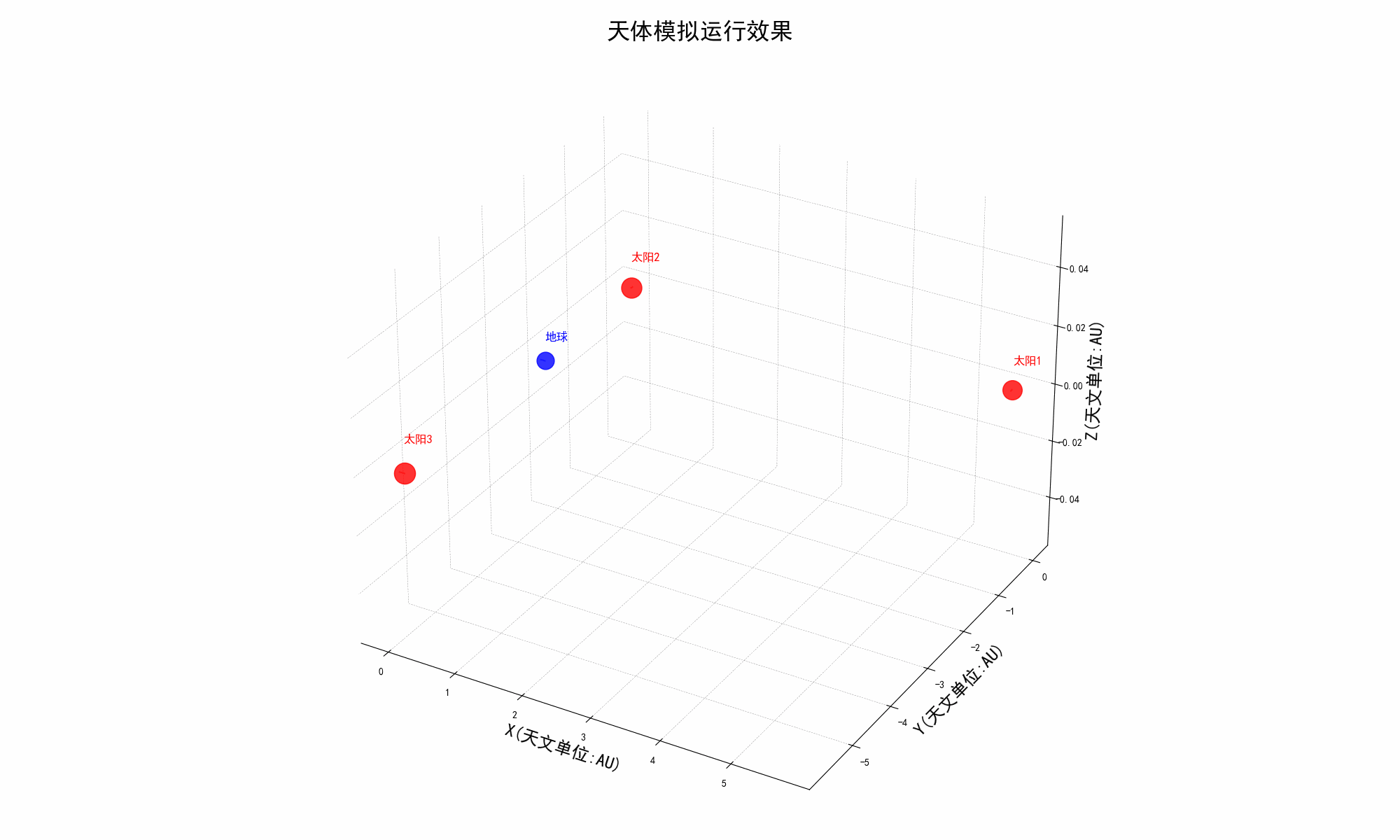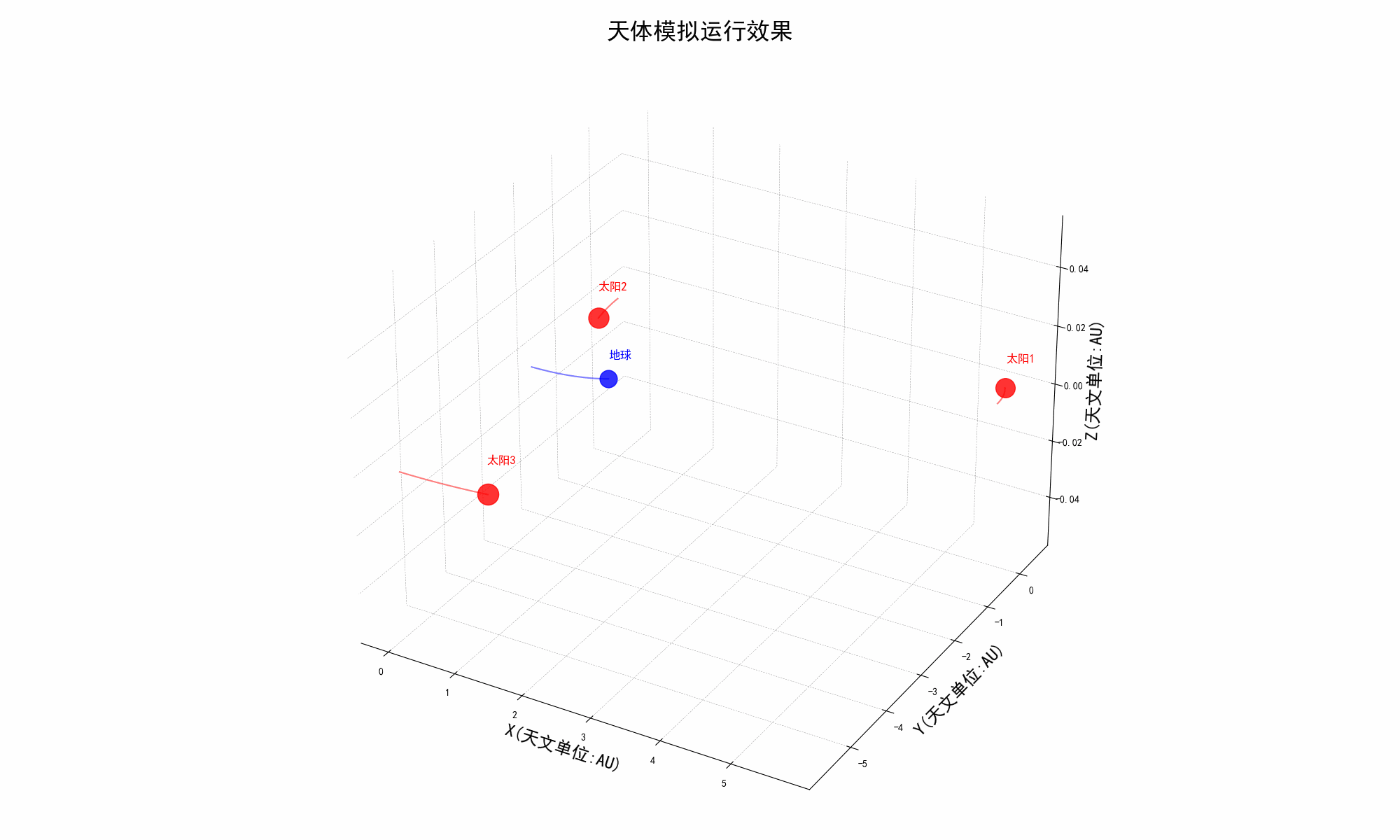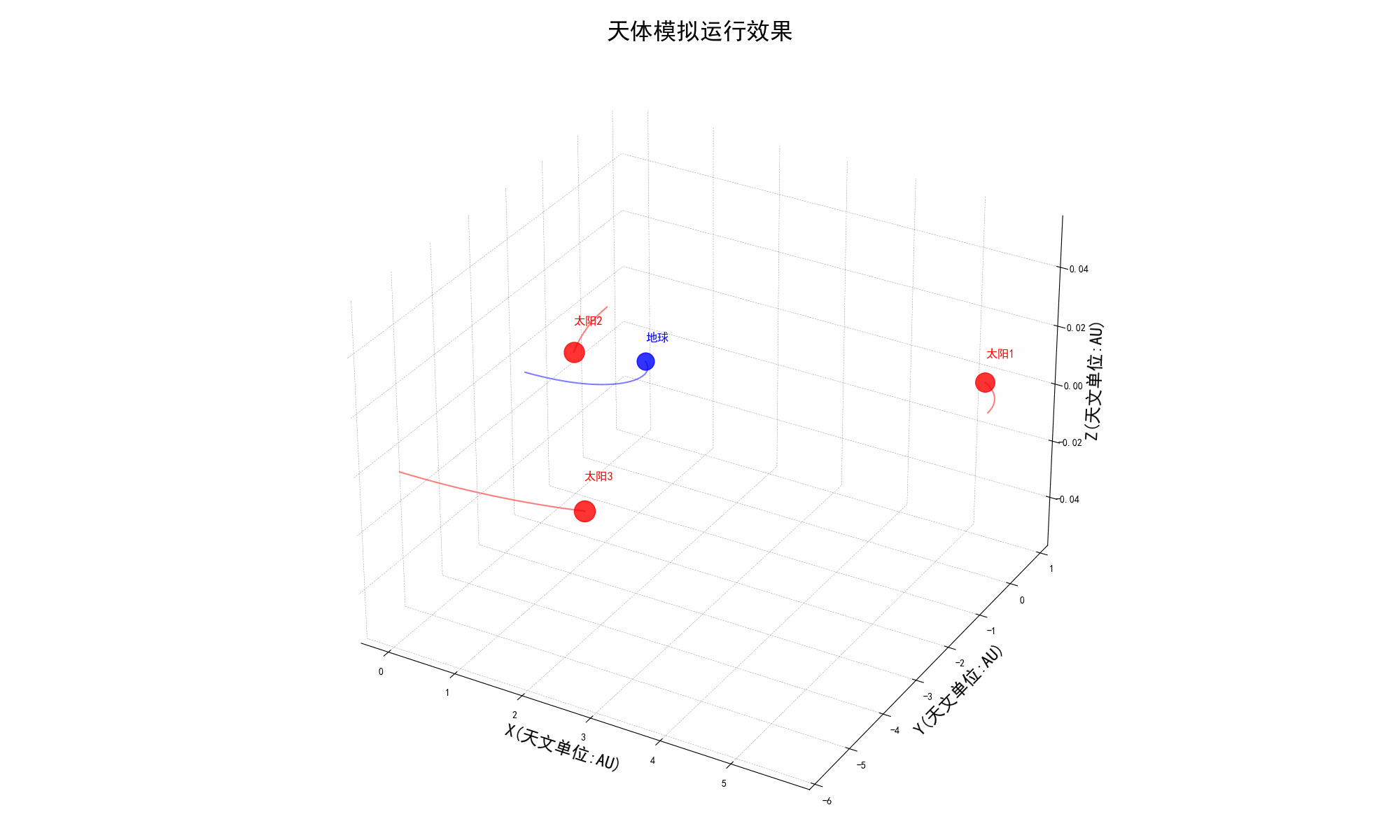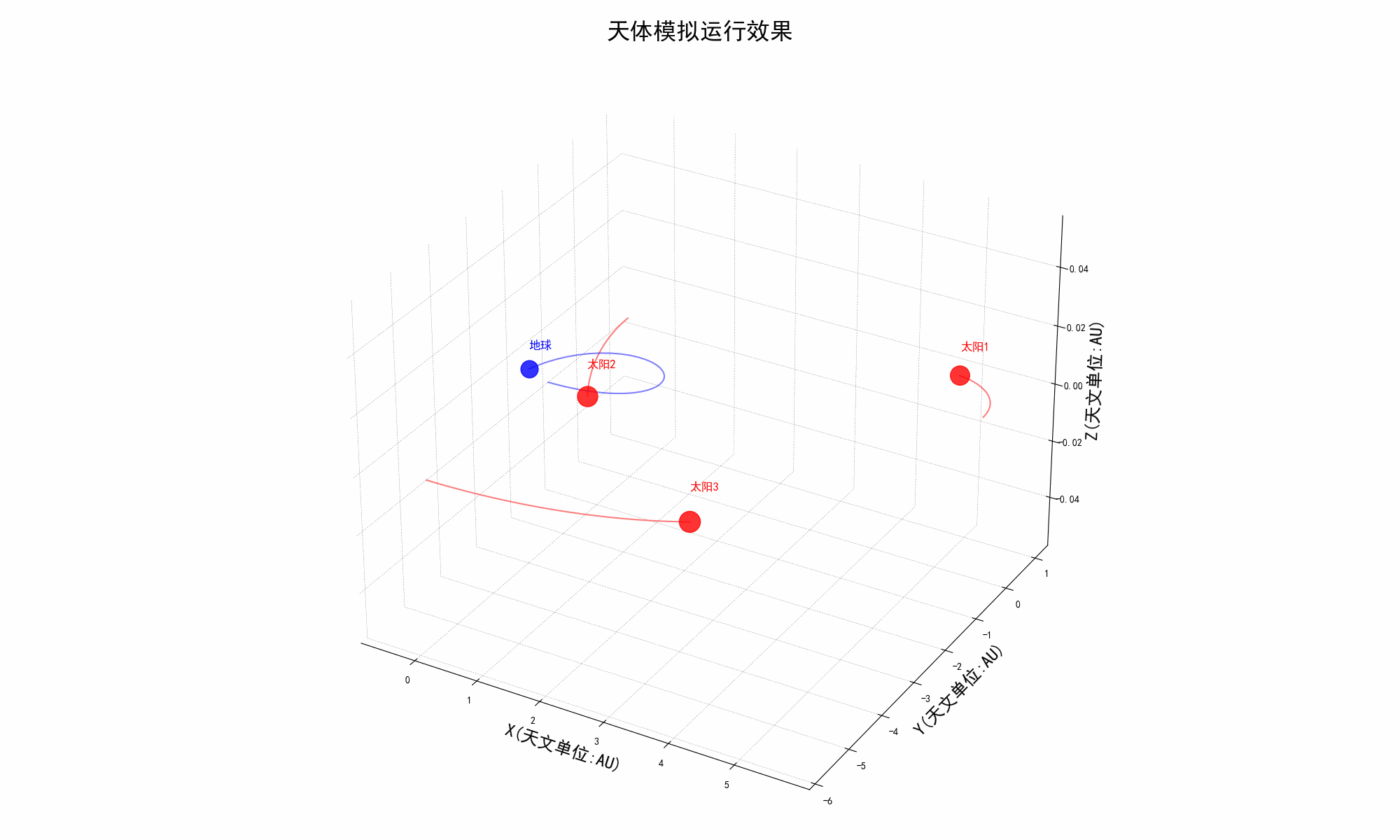
太阳系三体模拟器
介绍 《三体》是刘慈欣创作的长篇科幻小说,文中提到的三体问题比较复杂和无解。 该项目代码就是利用 Python 来模拟三体的运行,此项目代码完全共享,欢迎下载。 我们可以自己通过调整天体的初始坐标、质量和矢量速度等等参数来自定义各种场景…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...
