【力扣题解】P501-二叉搜索树中的众数-Java题解

👨💻博客主页:@花无缺
欢迎 点赞👍 收藏⭐ 留言📝 加关注✅!
本文由 花无缺 原创收录于专栏 【力扣题解】
文章目录
- 【力扣题解】P501-二叉搜索树中的众数-Java题解
- 🌏题目描述
- 💡题解
- 🌏总结
【力扣题解】P501-二叉搜索树中的众数-Java题解
P501-二叉搜索树中的众数
🌏题目描述
给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。
如果树中有不止一个众数,可以按 任意顺序 返回。
假定 BST 满足如下定义:
- 结点左子树中所含节点的值 小于等于 当前节点的值
- 结点右子树中所含节点的值 大于等于 当前节点的值
- 左子树和右子树都是二叉搜索树
示例 1:

输入:root = [1,null,2,2]
输出:[2]
示例 2:
输入:root = [0]
输出:[0]
提示:
- 树中节点的数目在范围
[1, 104]内 -105 <= Node.val <= 105
💡题解
递归:
// 节点值的最大出现频率
int maxCount = Integer.MIN_VALUE;
// 统计频率
int count = 0;
List<Integer> res = new LinkedList<>();
// 保存上一个遍历的节点
TreeNode pre = null;
public int[] findMode(TreeNode root) {dfs(root);int[] a = new int[res.size()];for (int i = 0; i < a.length; i++) {a[i] = res.get(i);}return a;
}
public void dfs(TreeNode root) {if (root == null) {return;}dfs(root.left);// 当前节点是第一个节点, count 为 1if (pre == null) {count = 1;// 当前节点和前一个节点值相同, count++} else if (pre.val == root.val) {count++;// 当前节点和前一个节点不同, count 变为 1} else {count = 1;}// 更新 pre 节点pre = root;// 如果当前统计到的节点值次数和最大节点值次数相同// 就放入列表 resif (count == maxCount) {res.add(root.val);}// 如果 count > maxCount, 那么就更新 maxCount// 然后先清空 res, 再将当前节点值加入列表 resif (count > maxCount) {maxCount = count;res.clear();res.add(root.val);}dfs(root.right);
}
迭代:
public int[] findMode(TreeNode root) {Deque<TreeNode> stack = new LinkedList<>();TreeNode cur = root;TreeNode pre = null;// 节点值的最大出现频率int maxCount = Integer.MIN_VALUE;// 统计频率int count = 0;List<Integer> res = new LinkedList<>();while (!stack.isEmpty() || cur != null) {if (cur != null) {stack.offerLast(cur);cur = cur.left;} else {cur = stack.pollLast();// 当前节点是第一个节点, count 为 1if (pre == null) {count = 1;// 当前节点和前一个节点值相同, count++} else if (pre.val == cur.val) {count++;// 当前节点和前一个节点不同, count 变为 1} else {count = 1;}// 更新 pre 节点pre = cur;// 如果当前统计到的节点值次数和最大节点值次数相同// 就放入列表 resif (count == maxCount) {res.add(cur.val);}// 如果 count > maxCount, 那么就更新 maxCount// 然后先清空 res, 再将当前节点值加入列表 resif (count > maxCount) {maxCount = count;res.clear();res.add(cur.val);}cur = cur.right;}}int[] a = new int[res.size()];for (int i = 0; i < a.length; i++) {a[i] = res.get(i);}return a;
}
时间复杂度:O(n),需要遍历二叉搜索树的所有节点,节点数为 n。
🌏总结
这个题要求我们查找二叉搜索树中的众数,也就是出现次数最多的一个或者多个节点值,按照一般的做法,我们会将二叉搜索树的节点值放到一个数组中,对数组进行排序,然后使用双指针遍历来获取数组中的众数,但是此题我们可以直接在遍历的过程中获取众数,为什么呢?因为根据二叉搜索树的特性,我们知道二叉搜索树的中序序列是一个有序的递增序列,所以我们可以在中序遍历二叉搜索树的时候同时对节点进行操作,从而获取到众数。
同样,在处理节点时,我们采用双指针法,pre 指向上一个遍历过的节点,然后使用当前节点和 pre 指向的节点进行比较,如果相等,则统计变量 count++,否则重置为 1,当然要注意,当我们遍历第一个节点的时候,pre 为 null,这时候 count 也为 1,也就是当前节点出现了一次。
然后每一次遍历之后,我们要将当前节点频次 count 和最大频次 maxCount 作比较,只要相等,就将当前节点值加入结果列表 res,但是有可能当前节点的频次还会增多,这怎么办呢?这就要到一下步骤了,如果当前频次 count 大于 maxCount,那么就更新 maxCount,接着我们要清空 res,这样就避免了出现错误结果的情况,然后将当前节点值加入 res。
以上我也给出了迭代法的代码,和递归代码的逻辑是完全一样的。
作者:花无缺(huawuque404.com)
🌸欢迎
关注我的博客:花无缺-每一个不曾起舞的日子都是对生命的辜负~
🍻一起进步-刷题专栏:【力扣题解】
🥇往期精彩好文:
📢【全网最全爱心代码仓库】
📢【CSS选择器全解指南】
📢【HTML万字详解】
你们的点赞👍 收藏⭐ 留言📝 关注✅
是我持续创作,输出优质内容的最大动力!
谢谢!
相关文章:

【力扣题解】P501-二叉搜索树中的众数-Java题解
👨💻博客主页:花无缺 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 本文由 花无缺 原创 收录于专栏 【力扣题解】 文章目录 【力扣题解】P501-二叉搜索树中的众数-Java题解🌏题目描述💡题解…...
Wnmp本地部署结合内网穿透实现任意浏览器远程访问本地服务
最近,我发现了一个超级强大的人工智能学习网站。它以通俗易懂的方式呈现复杂的概念,而且内容风趣幽默。我觉得它对大家可能会有所帮助,所以我在此分享。点击这里跳转到网站。 文章目录 前言1.Wnmp下载安装2.Wnmp设置3.安装cpolar内网穿透3.1…...
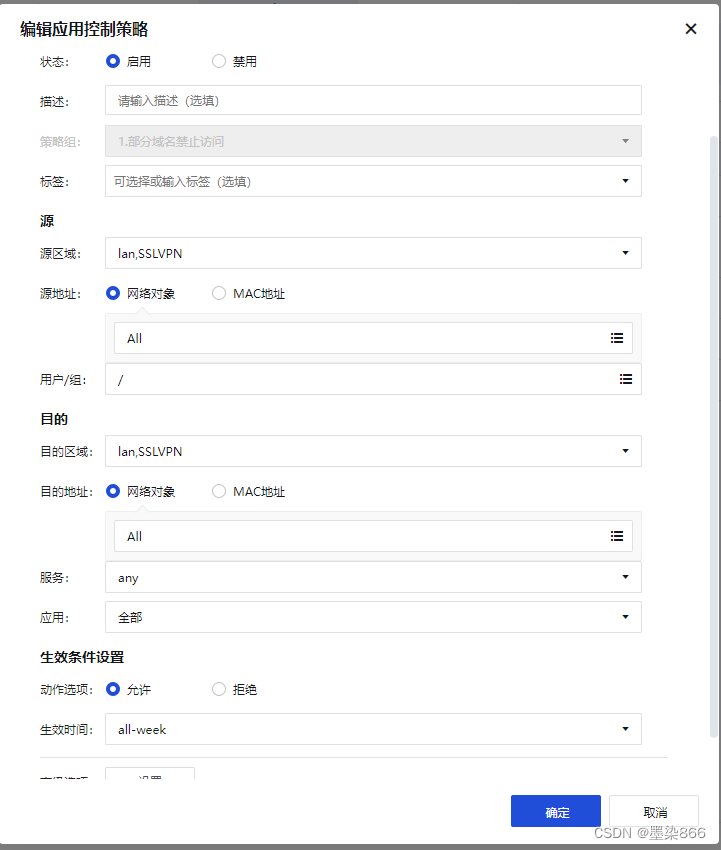
深信服AF防火墙配置SSL VPN
防火墙版本:8.0.85 需提前确认防火墙是是否有SSL VPN的授权,确认授权用户数量 1、确认内外网接口划分 2、网络→SSL VPN,选择内外网接口地址 3、SSL VPN→用户管理→新增一个SSL VPN的用户 4、新增L3VPN资源,类型选择Other&…...
在Spring Cloud中使用Gateway 网关
我们在上述文章中介绍了相关Spring Cloud的五大核心组件,现在我们来了解一下关于Spring Cloud的网关,关于使用网关,我们同时也需要知道他在一个架构中起到的作用,并且,我们需要知道网关具体的相关功能,本篇…...

【Python】配置环境变量
Python配置Windows系统环境变量 打开电脑属性 ——> 高级系统设置 ——> 高级 ——> 环境变量 Python安装目录 D:\Program Files\Python39 winR打开运行,输入cmd打开命令窗口 python -V...

使用.Net nanoFramework 驱动ESP32的OLED显示屏
本文介绍如何使用.Net nanoFramework 驱动ESP32的OLED显示屏。我们将会从最基础的部分开始,逐步深入,让你能够理解并实现整个过程。无论你是初学者还是有一定经验的开发者,这篇文章都会对你有所帮助。 1. 硬件准备 1.1 ESP32开发板 这里我们…...

0基础学习VR全景平台篇第134篇:720VR全景,云台调整节点
相机、云台和脚架全套设备组装完成后需要进行调校才能开始拍摄。这一节,我们将主要介绍云台调整的两个内容:对中心靶、调三点一线。(后附调校原理) 云台部件名称 一、调节准备 (一)对于安装好的云台 1.检…...

扫地机器人地图与用户终端的同步
以下内容为本人的学习笔记,如需要转载,请声明原文链接 微信公众号「ENG八戒」https://mp.weixin.qq.com/s/APaJheSbgTW3jNssWsp5Ng 地图数据来源于机器人算法模块,一般通过SLAM算法完成建图的过程。 建图过程中,基础数据涉及到各…...

使用机器学习进行语法错误检测/纠正
@francescofranco_39234 一、说明 一般的学习,特别是深度学习,促进了自然语言处理。各种模型使人们能够执行机器翻译、文本摘要和情感分析——仅举几个用例。今天,我们将研究另一个流行的用途:我们将使用Gramformer构建一个用于机器学习语法错误检测和纠正的管道。 阅读本文…...

从0到1快速入门ETLCloud
一、ETLCloud的介绍 ETL是将业务系统的数据经过抽取(Extract)、清洗转换(Transform)之后加载(Load)到数据仓库的过程,目的是将企业中的分散、凌乱、标准不统一的数据整合到一起,为企…...
QT上位机开发(会员管理软件)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 前面我们学习了ini文件的解析办法,通过QSettings类就可以很轻松地访问ini文件里面的数据。除了ini文件之外,另外一种经常出…...

线性代数笔记3 1.1
学习视频: 2.2 矩阵运算(二)_哔哩哔哩_bilibili 包括内容: p10矩阵运算(二) p11特殊矩阵 p12逆矩阵(一) p13逆矩阵(二)...
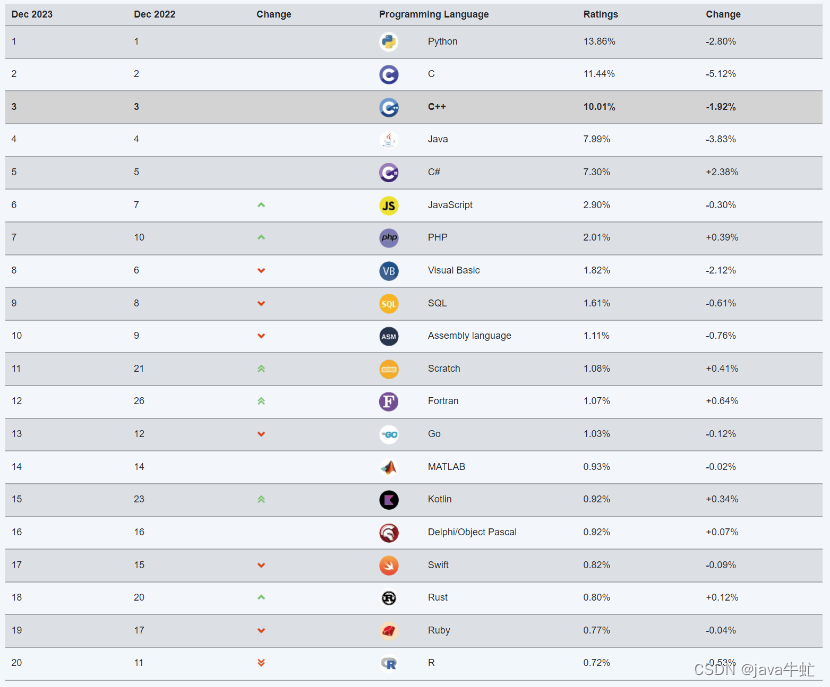
2023年12月编程语言排行榜
TIOBE Index for December 2023 December Headline: C# on its way to become programming language of the year 2023 2023年12月的TIOBE指数:12月头条:c#将成为2023年最佳编程语言 Yes, I know, we have been here before. At the end of 2022, it looked like …...

Redis VS Memcached:选择哪个更适合您的应用?
目录 1、前言 2、概念简介 2.1 Redis 2.2 Memcached 3、数据模型 4、持久性 5、分布式能力 6、性能和扩展性 7、如何选择适合您引用的缓存系统 8、结语 1、前言 Redis和Memcached都是常见的内存缓存系统,用于提升应用程序的性能和可扩展性。它们都具有高…...
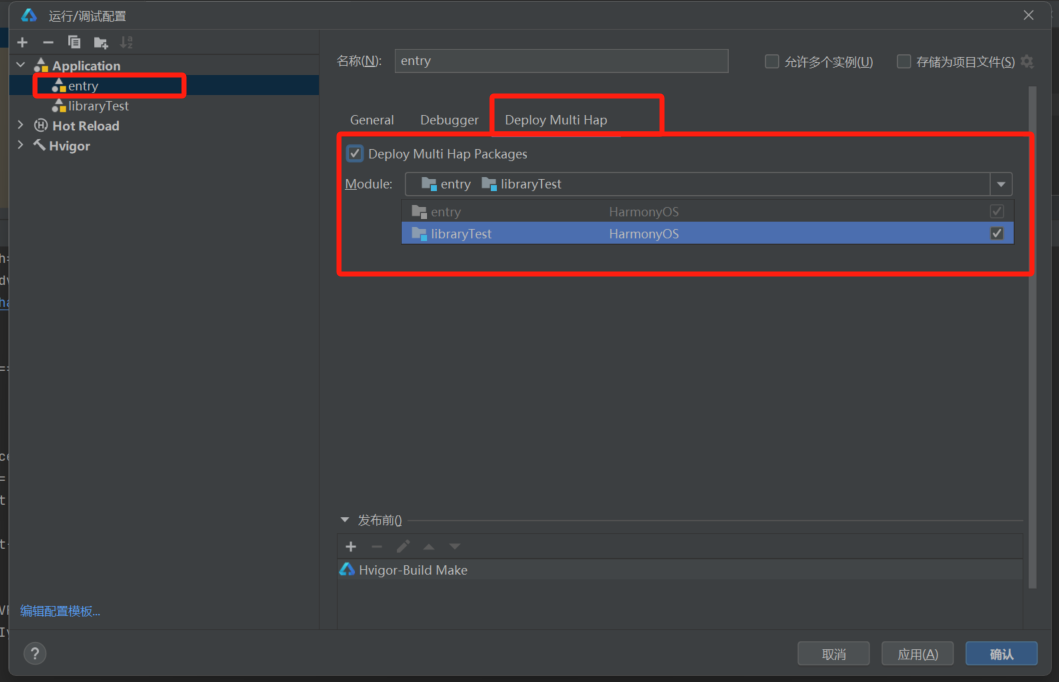
【HarmonyOS开发】共享包HAR和HSP的创建和使用以及三方库的发布
OpenHarmony提供了两种共享包,HAR(Harmony Archive)静态共享包,和HSP(Harmony Shared Package)动态共享包。 HAR与HSP都是为了实现代码和资源的共享,都可以包含代码、C库、资源和配置文件&…...
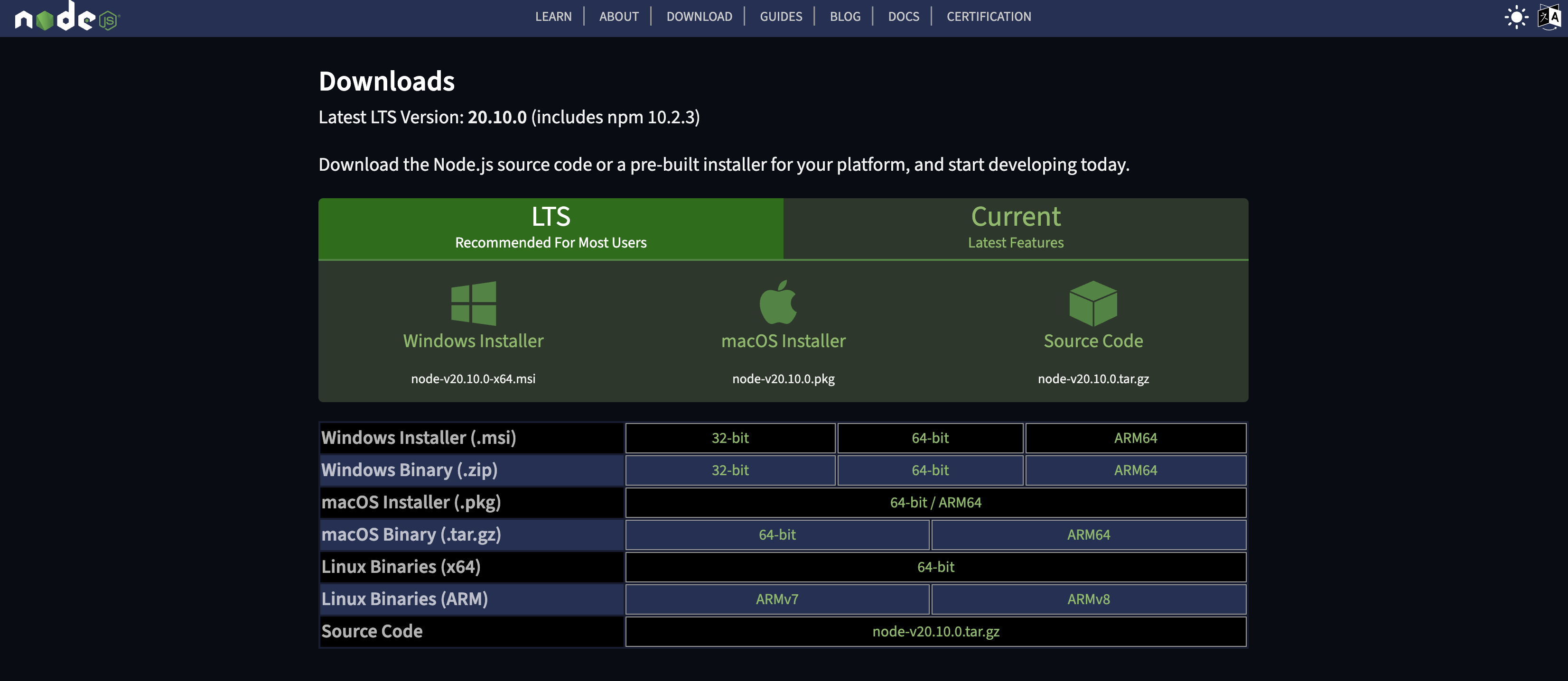
安装 Node.js、npm
安装 nodejs 安装Node.js的最简单的方法是通过软件包管理器。 Node.js官网:https://nodejs.org/en/download/ cd /usr/local/src/wget -c https://nodejs.org/dist/v18.16.0/node-v18.16.0-linux-x64.tar.xz xz -d node-v18.16.0-linux-x64.tar.xz tar -xf node…...
解决报错:找不到显卡
今天做实验碰到一个问题:torch找不到显卡: 打开任务管理器,独显直接没了,一度以为是要去修电脑了,突然想到上次做实验爆显存,屏蔽了gpu用cpu训练: import os os.environ["CUDA_DEVICE_OR…...

如何使用Node.js快速创建本地HTTP服务器并实现公网访问服务端
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...

【社交网络分析】课程考试复盘 + 相关资料补充
【社交网络分析】考试后复盘 相关资料补充 写在最前面论述1.描述Logistic回归模型构造损失函数的主要思想。它是如何把线性回归预测模型转化为二分类模型的。Logistic回归模型构造损失函数的主要思想Logistic回归如何将线性回归预测模型转化为二分类模型 2.社交网络分析中面临…...
算法——队列+宽搜(BFS)
队列这种数据结构大都服务于一个算法——宽搜(BFS)。宽搜还可以运用到二叉树、图、迷宫最短路径问题、拓扑排序等等 N叉数的层序遍历 N叉树的层序遍历 题目解析 给定一个 N 叉树,返回其节点值的_层序遍历_。(即从左到右&#…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...
