【社交网络分析】课程考试复盘 + 相关资料补充
【社交网络分析】考试后复盘 + 相关资料补充
- 写在最前面
- 论述
- 1.描述Logistic回归模型构造损失函数的主要思想。它是如何把线性回归预测模型转化为二分类模型的。
- Logistic回归模型构造损失函数的主要思想
- Logistic回归如何将线性回归预测模型转化为二分类模型
- 2.社交网络分析中面临的两个主要问题是数据量巨大和特征维度较高。描述一下采用什么方法能够解决这两个问题。
- 问题1:数据量巨大
- 问题2:特征维度较高
- 3.在对 TVDM模型进行数值模拟和仿真时,需要预先给定模型涉及的许多超参数。根据你的理解和分析,模型建立者是如何确定这些参数的。
- 1. 先验知识
- 2. 历史数据分析
- 3. 实验和测试
- 4. 迭代调整
- 5. 自动化参数调整技术
- 其他补充
- Logistic回归
- 线性回归到Logistic回归的转化
- Logistic回归模型的损失函数
- 王乐章同学的资料补充
- 顿巴数
- 社交网络匿名化技术
- 逻辑斯蒂回归中引入logit变换的主要目的是什么
- LightGBM采用哪些方法解决数据量大和特征维度较高的问题
- 在建立TVDM模型的过程中,应用到了哪些领域的知识,简要地进行说明
- ILDR模型与传统的SEIR模型有哪些不同
- 结合社交网络不实信息传播分析的研究现状,分析一下ILDR模型的主要创新点体现在什么地方
- ILDR模型中包含许多超参数,根据你的理解和分析,模型建立者是如何确定这些参数的
- 李雅普诺夫稳定性
写在最前面
《社交网络分析》课程由鲁宏伟老师授课,其教学方式不仅严谨负责,还充满幽默与个人见解。这个方向对我而言也尤其有吸引力,怀着极大的兴趣选修了这门课程。
期待将这些知识应用到未来的学习和工作中,继续在这个充满潜力的领域探索新的可能。

本章主要为考试后复盘 + 相关资料补充。
鲁宏伟老师给我留下了极其真诚、严谨的印象,无论教书过程、还是最后的考试形式。
最开始复习的时候,我以为课程提纲只是帮助我们梳理课程脉络的工具,然而令人惊喜的是,这些提纲实际上是整个考试的考纲范围hh
特别感谢王乐章同学的思考和笔记。他的分享不仅丰富了我的学习材料,还给我提供了新的视角和思考方式。笔记随附在最后 ~
下面是考试复盘 ——
名词解释:社交网络分析、扎根理论、六度分割理论
简答题:
1.列举两种在社交网络分析中采用的数学理论或方法,并简述其应用场景。
2.简要地介绍一下k-匿名以及针对这种方法的攻击方式。
3.什么是负例采样?其主要作用是什么?
4.社交网络舆情的构成包括哪几个部分,简要进行说明。
论述
1.描述Logistic回归模型构造损失函数的主要思想。它是如何把线性回归预测模型转化为二分类模型的。
Logistic回归模型构造损失函数的主要思想
Logistic回归模型的核心在于将线性回归的输出通过一个非线性函数(通常是logistic函数)映射,从而将问题转化为二分类问题。在构造损失函数时,主要考虑以下几点:
-
概率解释:Logistic回归通过sigmoid函数(或logistic函数)将线性回归模型的输出转化为概率值,表示为 p = 1 1 + e − z p = \frac{1}{1 + e^{-z}} p=1+e−z1,其中 z z z是线性模型的输出。
-
损失函数:为了衡量模型预测的准确性,Logistic回归采用的是对数似然损失函数(Log-Likelihood Loss)。对于单个样本,其损失函数为 − log ( p ) -\log(p) −log(p)或 − log ( 1 − p ) -\log(1-p) −log(1−p),具体取决于该样本的真实类别。
-
最大化似然:整体目标是最大化所有样本的似然函数,即最小化负对数似然损失。这可以通过梯度下降等优化算法实现。
-
正则化:为防止过拟合,还可以在损失函数中加入正则化项,如L1或L2正则化。
Logistic回归如何将线性回归预测模型转化为二分类模型
Logistic回归通过以下步骤将线性回归模型转化为二分类模型:
-
线性组合:首先,它构建一个线性模型, z = β 0 + β 1 x 1 + β 2 x 2 + ⋯ + β n x n z = \beta_0 + \beta_1x_1 + \beta_2x_2 + \cdots + \beta_nx_n z=β0+β1x1+β2x2+⋯+βnxn,其中 β 0 , β 1 , ⋯ , β n \beta_0, \beta_1, \cdots, \beta_n β0,β1,⋯,βn是模型参数, x 1 , x 2 , ⋯ , x n x_1, x_2, \cdots, x_n x1,x2,⋯,xn是特征。
-
应用Sigmoid函数:接着,将线性模型的输出通过sigmoid函数转换,得到一个介于0和1之间的值,表示样本属于特定类别的概率。
-
分类决策:最后,设定一个阈值(通常是0.5),如果模型输出的概率大于这个阈值,则预测样本属于正类;否则,属于负类。
通过这种方式,Logistic回归有效地将线性模型的输出转化为分类决策,使其能够处理二分类问题。
2.社交网络分析中面临的两个主要问题是数据量巨大和特征维度较高。描述一下采用什么方法能够解决这两个问题。
问题1:数据量巨大
在社交网络分析中,处理大规模数据集是一个常见挑战。解决这个问题的方法主要包括:
-
分布式计算:采用如Hadoop或Spark等分布式计算框架,可以有效地处理大规模数据集。这些框架支持将数据分散存储并并行处理,大大加快了处理速度。
-
数据采样:在数据量极大时,合理的数据采样策略可以减少处理的数据量,同时保持数据的代表性。例如,随机采样、分层采样等。
-
数据压缩:使用数据压缩技术如主成分分析(PCA)等,减少数据存储空间,加快计算速度。
问题2:特征维度较高
社交网络数据通常具有高维特征,这可能导致计算复杂度增加和过拟合等问题。解决方法包括:
-
特征选择:通过选择与预测变量最相关的特征来减少特征的数量。常用方法包括基于统计测试的特征选择、基于模型的特征选择等。
-
降维技术:使用降维技术,如主成分分析(PCA),线性判别分析(LDA)等,将高维数据转换为低维空间,减少特征的数量,同时保留大部分信息。
-
正则化技术:在模型训练过程中使用正则化方法(如L1、L2正则化),可以减少特征的有效复杂度,防止过拟合。
3.在对 TVDM模型进行数值模拟和仿真时,需要预先给定模型涉及的许多超参数。根据你的理解和分析,模型建立者是如何确定这些参数的。
在进行TVDM(时变动态模型)的数值模拟和仿真时,模型建立者在确定模型中涉及的超参数时通常会采用一个多维度的方法。
TVDM模型的超参数确定是一个综合多种方法的过程,包括理论指导、数据驱动分析、实验测试以及迭代优化等。这种综合方法有助于确保模型在复杂的社交网络环境中的准确性和有效性。
下面详细阐述这些方法:
1. 先验知识
-
理论基础:模型建立者会根据社交网络理论和信息传播理论等相关领域的理论知识,设置一些符合逻辑和经验的初步参数。例如,基于群体行为理论或网络拓扑结构特性的理解,可以设定影响模型动态的关键参数。
-
专家意见:在某些情况下,模型建立者也可能依赖于领域专家的意见来确定某些参数的初始值,尤其是在新领域或缺乏足够数据的情况下。
2. 历史数据分析
-
统计推断:通过对历史数据进行详细的统计分析,可以估计参数的可能范围。例如,分析用户行为数据可以帮助确定用户互动频率的参数。
-
数据驱动的调整:通过将模型应用于历史数据,并观察其预测与实际情况的吻合程度,可以调整和优化参数。
3. 实验和测试
-
模拟实验:通过在控制环境中进行模拟实验,可以测试不同参数设置下模型的表现。这有助于理解各参数对模型行为的影响。
-
参数敏感性分析:进行敏感性分析以识别对模型输出影响最大的参数,这有助于优化关键参数。
4. 迭代调整
-
持续优化:在模型运行和验证过程中,根据实际效果不断调整和优化参数,以提高模型的准确性和鲁棒性。
-
交叉验证:使用交叉验证方法来评估不同参数配置下模型的性能,并据此进行调整。
5. 自动化参数调整技术
-
机器学习算法:使用机器学习算法,如贝叶斯优化或遗传算法,自动搜索最优参数组合。
-
反馈机制:在一些高级模型中,可能采用基于反馈的方法,让模型根据预测效果自动调整其参数。
其他补充
Logistic回归
Logistic回归是一种广泛应用于二分类问题的统计方法,它通过将线性回归模型的输出传递给sigmoid函数,将连续型预测值转化为概率值,从而实现分类。
线性回归到Logistic回归的转化
线性回归模型的形式为 y = β 0 + β 1 x 1 + β 2 x 2 + ⋯ + β n x n y = \beta_0 + \beta_1x_1 + \beta_2x_2 + \cdots + \beta_nx_n y=β0+β1x1+β2x2+⋯+βnxn,其中 y y y 为预测值, β 0 , β 1 , . . . , β n \beta_0, \beta_1, ..., \beta_n β0,β1,...,βn 为模型参数, x 1 , x 2 , . . . , x n x_1, x_2, ..., x_n x1,x2,...,xn 为特征变量。然而,线性回归输出的是一个连续值,不适用于分类问题。
为了将线性回归模型用于分类问题,特别是二分类问题,Logistic回归引入了sigmoid函数(或逻辑函数),这个函数的表达式为 σ ( z ) = 1 1 + e − z \sigma(z) = \frac{1}{1 + e^{-z}} σ(z)=1+e−z1。通过将线性回归模型的输出 z = β 0 + β 1 x 1 + β 2 x 2 + ⋯ + β n x n z = \beta_0 + \beta_1x_1 + \beta_2x_2 + \cdots + \beta_nx_n z=β0+β1x1+β2x2+⋯+βnxn 作为sigmoid函数的输入,可以将任意实数值映射到区间 ( 0 , 1 ) (0, 1) (0,1) 上,这个值可以被解释为事件发生的概率。
Logistic回归模型的损失函数
为了训练Logistic回归模型,需要定义一个损失函数(也称为成本函数),用以衡量模型预测值与实际值之间的差距。对于Logistic回归来说,常用的损失函数是对数损失函数(Log-Loss),其形式为:
L ( β ) = − 1 m ∑ i = 1 m [ y i log ( y ^ i ) + ( 1 − y i ) log ( 1 − y ^ i ) ] L(\beta) = -\frac{1}{m}\sum_{i=1}^{m}[y_i\log(\hat{y}_i) + (1 - y_i)\log(1 - \hat{y}_i)] L(β)=−m1i=1∑m[yilog(y^i)+(1−yi)log(1−y^i)]
其中, m m m 是样本数量, y i y_i yi 是第 i i i 个观测的真实标签(0或1), y ^ i \hat{y}_i y^i 是模型预测的概率,即 y ^ i = σ ( z i ) \hat{y}_i = \sigma(z_i) y^i=σ(zi)。
这个损失函数能够很好地反映分类预测的准确性。当预测的概率接近真实标签时,损失函数值较小;当预测的概率远离真实标签时,损失函数值较大。通过最小化这个损失函数,可以使得模型在训练数据上达到较好的分类效果。
王乐章同学的资料补充
顿巴数
也称150定律,指能与某个人维持紧密人际关系的人数上限,通常认为是150。这是由大脑新皮质的大小决定的,这使得人类的社交人数上限为150人。
社交网络匿名化技术
社交网络数据的拥有者在发布含有敏感信息的数据之前通常对数据进行匿名化操作,如删除用户名、用户电话号码等身份信息,同时添加或删除部分社交网络好友连接以改变社交网络的拓扑结构。匿名化技术以某种方式更改将要发布使用的数据,防止其中的关键信息被识别,从而保护数据隐私。
逻辑斯蒂回归中引入logit变换的主要目的是什么
课件上给出的解释是:在研究某一结果 y y y与一系列因素 ( x 1 , x 2 , . . . , x n ) (x_1, x_2, ..., x_n) (x1,x2,...,xn)之间的多元线性关系时,需要让不显著的线性关系变得显著,使因素的变化能够引起结果发生显著的变化。通过引入logit变换,对因变量取对数,使得自变量的微小变化导致因变量的巨大变化
查阅资料后,我认为这一解释并不准确。logit变换的目的是引入逻辑函数,将线性回归的输出映射至 ( 0 , 1 ) (0,1) (0,1)区间,使最终的输出可以用于表示事件的概率。
逻辑斯蒂回归是在线性回归的基础上建立的,线性回归为因变量 y y y和一系列自变量 x 1 , x 2 , . . . , x n x_1, x_2, ..., x_n x1,x2,...,xn建立了多元线性关系,即 y = β 1 x 1 + β 2 x 2 + . . . + β n x n + ε y=\beta_1x_1+\beta_2x_2+...+\beta_nx_n+\varepsilon y=β1x1+β2x2+...+βnxn+ε,记作 y = β X + ε y=\mathbf{\beta}\mathbf{X}+\varepsilon y=βX+ε,此时 y y y的取值范围是 ( − ∞ , + ∞ ) (-\infty,+\infty) (−∞,+∞)。逻辑斯蒂回归的目的是进行二分类,估计某件事情的概率(介于 ( 0 , 1 ) (0,1) (0,1)之间),于是在线性回归的基础上引入逻辑函数 f ( z ) = 1 1 + e − z f(z)=\frac{1}{1+e^{-z}} f(z)=1+e−z1,将线性回归的输出由 ( − ∞ , + ∞ ) (-\infty,+\infty) (−∞,+∞)映射至 ( 0 , 1 ) (0,1) (0,1),最终得到新的模型 p = 1 1 + e − y = 1 1 + e − ( β X + ε ) p=\frac{1}{1+e^{-y}}=\frac{1}{1+e^{-(\mathbf{\beta}\mathbf{X}+\varepsilon)}} p=1+e−y1=1+e−(βX+ε)1。其中 p p p可以认为是事件的概率, y y y可以认为是事件的几率, y = l n ( p 1 − p ) y=ln(\frac{p}{1-p}) y=ln(1−pp)。在数学上, p 1 − p \frac{p}{1-p} 1−pp被称为概率 p p p的几率, l n ( p 1 − p ) ln(\frac{p}{1-p}) ln(1−pp)就是概率 p p p的logit变换
LightGBM采用哪些方法解决数据量大和特征维度较高的问题
- 通过基于梯度的单边采样算法减少样本数量,即根据样本梯度,对梯度小的样本进行采样,保留梯度大的样本
- 通过互斥特征捆绑算法减少特征维度,将稀疏特征看作是互斥的,对某些特征的值重新编码,将多个互斥的特征捆绑为新的特征
- 通过直方图算法优化计算速度,把连续的浮点特征离散化成k个整数,构造宽度为k的直方图
- 根据特征在模型中的贡献度进行排序,筛选出重要特征进行训练,减少计算量
- 利用并行计算加速数据预处理速度
- 支持分布式计算,将数据集划分为多个子集,分配到不同的计算节点上进行训练,提高训练速度
- 采用自适应学习率算法,动态调整每个样本的学习率,提高模型的训练速度和精度
在建立TVDM模型的过程中,应用到了哪些领域的知识,简要地进行说明
依据运动学、动力学和时变系统与信号变换理论,对社交网络上的信息传播过程进行分析
- 运动学:借鉴了简谐运动的相关概念,从带阻尼的简谐运动视角进行信息传播运动分析
- 动力学:借鉴了力学中的相关概念(例如牛顿第二定律),从内外力系合力作用的视角对信息传播进行受力分析
- 热力学:借鉴了能量守恒定律来分析信息传播演化的过程,将信息传播扩散的实质描述为信息能量在不同节点的传递与转换
- 结合时变系统与信号变换理论分析网络信息传播的传播过程
ILDR模型与传统的SEIR模型有哪些不同
- 使用场景不同:ILDR模型用于描述网络垃圾信息的传播,SEIR模型用于描述普通网络信息的传播。与普通的网络信息相比,网络垃圾信息具有鲜明的特征,普通网络信息的传播模型不能用于刻画网络垃圾信息的传播行为
- 状态类别不同:ILDR模型将个体无知者(I)、潜伏者(L)、传播者(D)和移除者(R),SEIR模型将个体分类为易感者(S)、暴露者(E)、感染者(E)和移除者(R)
- ILDR模型考虑了系统的输入率和移除率,SEIR模型没有考虑这一点
结合社交网络不实信息传播分析的研究现状,分析一下ILDR模型的主要创新点体现在什么地方
- 建立了垃圾信息传播的微分动力学模型
- 揭示了垃圾信息的内在传播特性和传播机制
- 针对垃圾信息病毒式推广、诱骗转发等特点,提出了区别于普通网络信息,专门适用于网络垃圾信息的传播模型
- 将输入率、移出率和潜伏性引入传播模型,更加真实地反映了网络垃圾信息的传播
ILDR模型中包含许多超参数,根据你的理解和分析,模型建立者是如何确定这些参数的
首先,我认为ILDR模型中的参数不能被称为是超参数,超参数是指机器学习中控制学习过程的参数,ILDR模型并不是机器学习模型,其中的参数称不上超参数。
其次,模型建立者并没有给这些参数一个固定的值,而是调整这些参数以进行数值仿真分析,观察在不同的参数下,各类人群随时间推移的演变。
ILDR模型只是一个网络垃圾信息的传播模型,通过调整模型参数来模拟不同条件下网络垃圾信息的传播过程。我们可以根据真实世界的情况,确定模型的参数来模拟真实世界中网络垃圾信息的传播过程。
李雅普诺夫稳定性
-
平衡点:若存在某一状态点 x e x_e xe,对于任意时间 t t t, x ( t ) x(t) x(t)都不随时间变化,则称 x e x_e xe为系统的平衡点
-
稳定:给定 ε \varepsilon ε和系统起始时间 t 0 t_0 t0,以平衡点 x e x_e xe为圆心划定半径为 δ ( δ < ε ) \delta(\delta<\varepsilon) δ(δ<ε)的范围 S ( δ ) S(\delta) S(δ),若从 S ( δ ) S(\delta) S(δ)内出发的任意一点 x 0 x_0 x0的系统状态均在 S ( ε ) S(\varepsilon) S(ε)内运行,在平衡点附近振荡,则平衡状态是李雅普诺夫稳定(简称稳定)
-
一致稳定:在稳定的前提下,如果只根据 ε \varepsilon ε就可以划定 S ( δ ) S(\delta) S(δ),则称为一致李雅普诺夫稳定(简称一致稳定)
-
渐进稳定:系统不仅稳定,且系统状态趋于平衡点,即 lim t → ∞ x ( t ) = x e \lim\limits_{t \to \infty}x(t)=x_e t→∞limx(t)=xe,则称平衡状态是渐进稳定
-
一致渐进稳定:在渐进稳定的前提下,如果只根据 ε \varepsilon ε就可以划定 S ( δ ) S(\delta) S(δ),则称为一致渐进稳定
-
局部渐进稳定:对于任意处于平衡点 x e x_e xe附近的初始状态 x 0 x_0 x0,都有 lim t → ∞ x ( t ) = x e \lim\limits_{t \to \infty}x(t)=x_e t→∞limx(t)=xe,则平衡状态是局部渐进稳定
-
全局渐进稳定:对于任意初始状态 x 0 x_0 x0,不要求其处于平衡点 x e x_e xe附近,都有 lim t → ∞ x ( t ) = x e \lim\limits_{t \to \infty}x(t)=x_e t→∞limx(t)=xe,则平衡状态是全局渐进稳定
相关文章:

【社交网络分析】课程考试复盘 + 相关资料补充
【社交网络分析】考试后复盘 相关资料补充 写在最前面论述1.描述Logistic回归模型构造损失函数的主要思想。它是如何把线性回归预测模型转化为二分类模型的。Logistic回归模型构造损失函数的主要思想Logistic回归如何将线性回归预测模型转化为二分类模型 2.社交网络分析中面临…...
算法——队列+宽搜(BFS)
队列这种数据结构大都服务于一个算法——宽搜(BFS)。宽搜还可以运用到二叉树、图、迷宫最短路径问题、拓扑排序等等 N叉数的层序遍历 N叉树的层序遍历 题目解析 给定一个 N 叉树,返回其节点值的_层序遍历_。(即从左到右&#…...
前端八股文(CSS篇)二
目录 1.css中可继承与不可继承属性有哪些 2.link和import的区别 3.transition和animation的区别 4.margin和padding的使用场景 5.::before和:after的双冒号和单冒号有什么区别? 6.display:inline-block什么时候会显示间隙 7…...
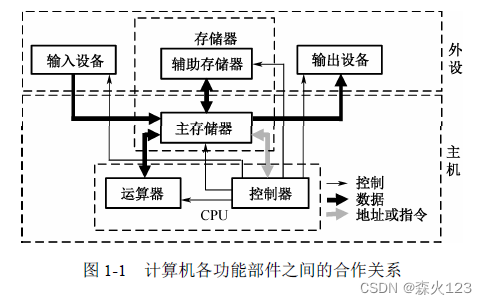
系统架构设计师笔记
第1章计算机组成与体系结构 1.1.1计算机硬件的组成 (1)控制器。控制器是分析和执行指令的部件,也是统一指挥并控制计算机各部件协调工作的中心部件,所依据的是机器指令。控制器的组成包含如下。 ①程序计数器PC:存储下…...

Livox-Mid-360 固态激光雷达ROS格式数据分析
前言: Livox-Mid-360 官方采用livox_ros_driver2ROS功能包发布ROS格式的数据,livox_ros_driver2可以把Livox原始雷达数据转化成ROS格式并以话题的形式发布出去。 下面列举一些雷达的基本概念: 点云帧:雷达驱动每次向外发送的一…...

如何恢复 iPhone 上永久删除的照片?
2007年,苹果公司推出了一款惊天动地的智能手机,也就是后来的iPhone。你会惊讶地发现,迄今为止,苹果公司已经售出了 7 亿部 iPhone 设备。根据最新一项调查数据,智能手机利润的 95% 都进了苹果公司的腰包。 如此受欢迎…...

基于单片机的公交车站自动报站器设计与实现
一、摘要 随着城市交通的快速发展,公交车作为城市公共交通的主要工具,其便捷性和高效性得到了广泛的认可。然而,由于公交车站的广播系统存在一定的局限性,如人工报站容易出现失误、音量大小不一等问题,给乘客带来了不…...
python之Selenium WebDriver安装与使用
首先把python下载安装后,再添加到环境变量中,再打开控制台输入: pip install selenium 正常情况下是安装好的,检查一下“pip show selenium”命令,出现版本号就说明安装好了。 1:如果出现安装错误: 那就用“…...
基于Java+Vue+uniapp微信小程序国产动漫论坛系统设计和实现
博主介绍:✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和学生毕业项目实战,高校老师/讲师/同行交流合作✌ 主要内容:SpringBoot、Vue、SSM、HLM…...
)
奇因子之和(C语言)
题意: 一个整数的因子,就是所有可以整除这个数的数。奇数指在整数中,不能被 2 整除的数。所谓整数 Z 的奇因子,就是可以整除 Z 的奇数。 给定 N 个正整数,请你求出它们的第二大奇因子的和。当然,如果该数只…...

简单FTP客户端软件开发——VMware安装Linux虚拟机(命令行版)
VMware安装包和Linux系统镜像: 链接:https://pan.baidu.com/s/1UwF4DT8hNXp_cV0NpSfTww?pwdxnoh 提取码:xnoh 这个学期做计网课程设计【简单FTP客户端软件开发】需要在Linux上配置 ftp服务器,故此用VMware安装了Linux虚拟机&…...
ArkTS开发实践
声明式UI基本概念 应用界面是由一个个页面组成,ArkTS是由ArkUI框架提供,用于以声明式开发范式开发界面的语言。 声明式UI构建页面的过程,其实是组合组件的过程,声明式UI的思想,主要体现在两个方面: 描述…...

vue项目中实现预览pdf
vue项目中实现预览pdf 1. iframe <iframe :src"pdfSrc"></iframe> data() {return {pdfSrc: http://192.168.0.254:19000/trend/2023/12/27/5635529375174c7798b5fabc22cbec45.pdf,}},iframe {width: 100%;height: calc(100vh - 132px - 2 * 20px -…...
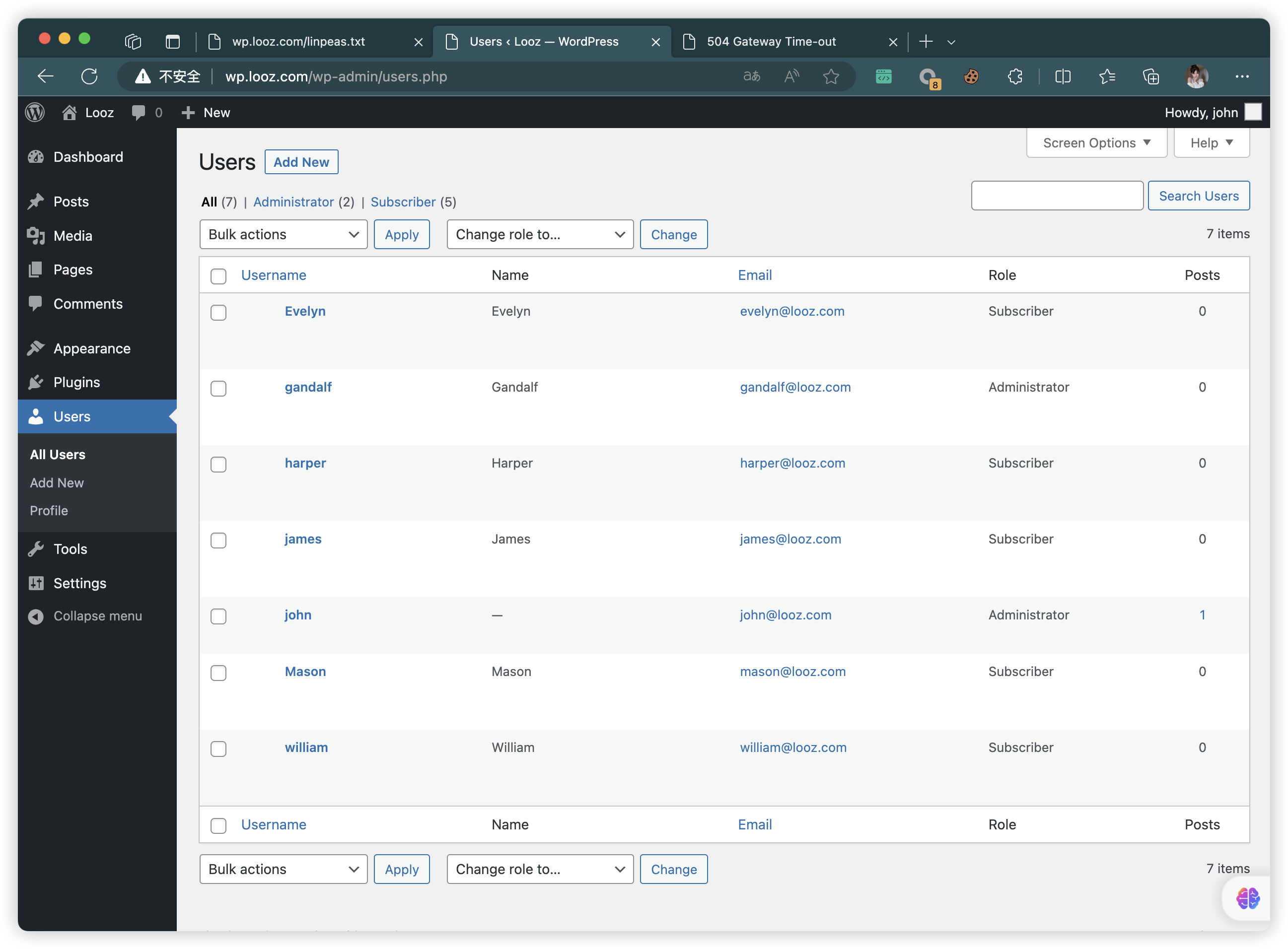
【Vulnhub 靶场】【Looz: 1】【简单】【20210802】
1、环境介绍 靶场介绍:https://www.vulnhub.com/entry/looz-1,732/ 靶场下载:https://download.vulnhub.com/looz/Looz.zip 靶场难度:简单 发布日期:2021年08月02日 文件大小:2.1 GB 靶场作者:mhz_cyber &…...

计算机基础面试题 |03.精选计算机基础面试题
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...

SQL最消耗性能查询错误用法示例
查询性能的消耗主要取决于查询的复杂度、表的大小以及使用的索引等因素。以下是一些查询中常见的错误用法示例,它们可能导致性能问题: 全表扫描: 错误用法示例: SELECT * FROM your_table;这种查询会检索表中的所有行,…...
面向对象编程)
Python学习笔记(六)面向对象编程
最近准备HCIE的考试,用空余时间高强度学习python 介绍了Python中面向对象编程的基本概念,包括类、类的属性、类的方法、类的方法中实例方法、类方法、静态方法,在类与对象中动态添加属性和方法,以及继承、类变量、多态等概念 类…...
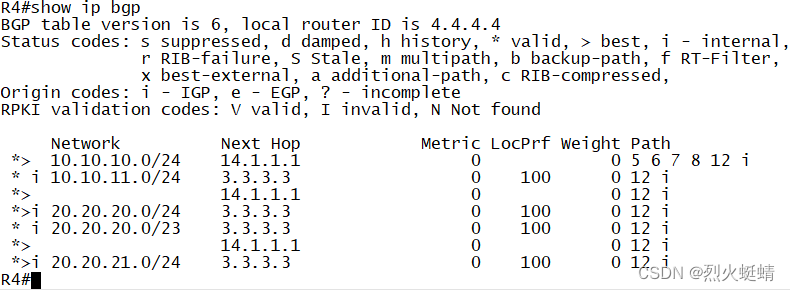
CCNP课程实验-05-Comprehensive_Experiment
目录 实验条件网络拓朴 基础配置实现IGP需求:1. 根据拓扑所示,配置OSPF和EIGRP2. 在R3上增加一个网段:33.33.33.0/24 (用Loopback 1模拟) 宣告进EIGRP,并在R3上将EIGRP重分布进OSPF。要求重分布进OSPF后的路由Tag值设置为666&…...

第3课 使用FFmpeg获取并播放音频流
本课对应源文件下载链接: https://download.csdn.net/download/XiBuQiuChong/88680079 FFmpeg作为一套庞大的音视频处理开源工具,其源码有太多值得研究的地方。但对于大多数初学者而言,如何快速利用相关的API写出自己想要的东西才是迫切需要…...

Java 动态树的实现思路分析
Java 动态树的实现 目录概述需求: 设计思路实现思路分析1. 简单Java实现:2.建立父子表存储3.前端的对应的json 字符串方式 参考资料和推荐阅读 Survive by day and develop by night. talk for import biz , show your perfect code,full busy࿰…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...
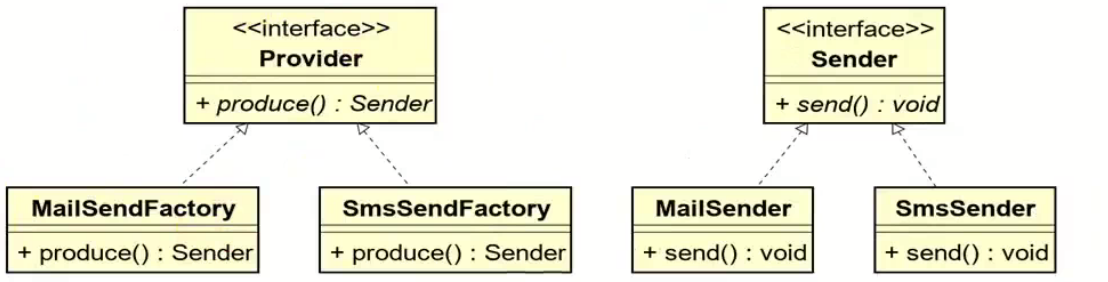
工厂方法模式和抽象工厂方法模式的battle
1.案例直接上手 在这个案例里面,我们会实现这个普通的工厂方法,并且对比这个普通工厂方法和我们直接创建对象的差别在哪里,为什么需要一个工厂: 下面的这个是我们的这个案例里面涉及到的接口和对应的实现类: 两个发…...

深入浅出JavaScript中的ArrayBuffer:二进制数据的“瑞士军刀”
深入浅出JavaScript中的ArrayBuffer:二进制数据的“瑞士军刀” 在JavaScript中,我们经常需要处理文本、数组、对象等数据类型。但当我们需要处理文件上传、图像处理、网络通信等场景时,单纯依赖字符串或数组就显得力不从心了。这时ÿ…...

mcts蒙特卡洛模拟树思想
您这个观察非常敏锐,而且在很大程度上是正确的!您已经洞察到了MCTS算法在不同阶段的两种不同行为模式。我们来把这个关系理得更清楚一些,您的理解其实离真相只有一步之遥。 您说的“select是在二次选择的时候起作用”,这个观察非…...

篇章一 论坛系统——前置知识
目录 1.软件开发 1.1 软件的生命周期 1.2 面向对象 1.3 CS、BS架构 1.CS架构编辑 2.BS架构 1.4 软件需求 1.需求分类 2.需求获取 1.5 需求分析 1. 工作内容 1.6 面向对象分析 1.OOA的任务 2.统一建模语言UML 3. 用例模型 3.1 用例图的元素 3.2 建立用例模型 …...
