对偶问题的基本性质
写于:2024年1月3日晚
修改于:
原规划与对偶规划
| 原规划 | 对偶规划 |
|---|---|
| max z = C T X s.t. { A X ≤ b , 其中 X ( m ∗ 1 ) X ≥ 0 \begin{aligned} & \max \mathrm{z}=\mathbf{C}^T \mathbf{X} \\ & \text { s.t. }\left\{\begin{array}{l}\mathbf{A X} \leq \mathbf{b}, \quad \text { 其中 } \mathrm{X}_{\left(\mathrm{m}^* 1\right)} \\ \mathbf{X} \geq \mathbf{0}\end{array}\right.\end{aligned} maxz=CTX s.t. {AX≤b, 其中 X(m∗1)X≥0 | min w = Y b s.t. { Y A ≥ C T , 其中 Y ( 1 ∗ n ) Y ≥ 0 \begin{aligned} & \min w=\mathbf{Y b} \\ & \text { s.t. }\left\{\begin{array}{l}\mathbf{Y A} \geq \mathbf{C}^T, \text { 其中 } \mathrm{Y}_{\left(1^* \mathrm{n}\right)} \\ \mathbf{Y} \geq 0\end{array}\right.\end{aligned} minw=Yb s.t. {YA≥CT, 其中 Y(1∗n)Y≥0 |
| max z = ∑ j = 1 n c j x j s.t. { ∑ j = 1 n a i j x j ≤ b i ( i = 1 , 2 , … , m ) x j ≥ 0 ( j = 1 , 2 , … , n ) \begin{aligned} & \max \mathrm{z}=\sum_{j=1}^n c_j x_j \\ & \text { s.t. }\left\{\begin{array}{l}\sum_{j=1}^n a_{i j} x_j \leq b_i(i=1,2, \ldots, m) \\ x_j \geq 0(j=1,2, \ldots, n)\end{array}\right.\end{aligned} maxz=j=1∑ncjxj s.t. {∑j=1naijxj≤bi(i=1,2,…,m)xj≥0(j=1,2,…,n) | min w = ∑ i = 1 m b i y i s.t. { ∑ i = 1 m a i j y i ≥ c j ( j = 1 , 2 , … , n ) y i ≥ 0 ( i = 1 , 2 , … , m ) \begin{aligned} & \min w=\sum_{i=1}^m b_i y_i \\ & \text { s.t. }\left\{\begin{array}{l}\sum_{i=1}^m a_{i j} y_i \geq c_j(j=1,2, \ldots, n) \\ y_i \geq 0(i=1,2, \ldots, m)\end{array}\right.\end{aligned} minw=i=1∑mbiyi s.t. {∑i=1maijyi≥cj(j=1,2,…,n)yi≥0(i=1,2,…,m) |
对称性:对偶问题的对偶问题是原问题。任何一个线性规划问题存在且有唯一的对偶问题。
弱对偶性:若 X ‾ \overline{\mathbf{X}} X 是原问题的可行解, Y ‾ \overline{\mathbf{Y}} Y 是对偶问题的可行解,则存在 C X ‾ ⩽ Y ‾ b \mathbf{C} \overline{\mathbf{X}} \leqslant \overline{\mathbf{Y}} \mathbf{b} CX⩽Yb。
原问题最优目标函数值是对偶目标函数值的下界,对偶问题最优目标函数值是原问题目标函数值的上界。

坐标轴理解: 坐标轴自左向右逐渐增大。如果原问题和对偶问题都有可行解 X ‾ 、 Y ‾ \overline{\mathbf{X}} 、 \overline{\mathbf{Y}} X、Y,那么说明原问题和对偶问题都存在某个可行解对应的函数值,而因为原问题为 max \max max 类型,则更优解会在 Z ∗ \mathrm{Z}^* Z∗ 右侧,而对偶问题为 m i n \mathrm{min} min 类型,更优解会在 W ∗ \mathrm{W}^* W∗ 左侧,两者一定会在某一处取得相同的最优目标函数值,因此存在 C X ‾ ⩽ Y ‾ b \mathbf{C} \overline{\mathbf{X}} \leqslant \overline{\mathbf{Y}} \mathbf{b} CX⩽Yb 。
将原问题和对偶问题看做是两个人在角力,目标函数值视为擂台。原问题自左向右冲,对偶问题自右向左冲,如果问题有可行解,那么就在擂台上,如果有无界解,那么就将对方挤出擂台。
无界性:
-
若原问题/对偶问题有无界解,那么对偶问题/原问题无可行解

如果原问题有无界解,说明原问题最优值随着坐标轴一直向右延伸,对偶问题被挤出擂台,所以对偶问题无可行解。 -
若原问题/对偶问题无可行解,那么对偶问题/原问题无可行解或有无界解
-
若原问题有可行解,而对偶问题无可行解,那么原问题有无界解
-
若对偶问题有可行解,而原问题无可行解,那么对偶问题有无界解
补充:原问题和对偶问题中有一个为无穷多/唯一最优解,无法退出另一个最优解的情况。
最优性:设 X ^ \widehat{\mathbf{X}} X 是原问题的可行解, Y ^ \widehat{\mathbf{Y}} Y 是对偶问题的可行解,当 C X ^ = Y ^ b \mathbf{C} \hat{\mathbf{X}}=\hat{\mathbf{Y}} \mathbf{b} CX^=Y^b 时, X ^ \hat{\mathbf{X}} X^、 Y ^ \hat{\mathbf{Y}} Y^ 是最优解。
对偶定理:
表述1:若原问题和对偶问题都有可行解,则都有最优解,而且最优解的目标函数值相等。
表述2:若原问题有最优解,则对偶问题也有最优解,而且目标函数值相等。
互补松驰定理:线性规划问题的最优解中,如果对应某一约束条件的对偶变量值非零,那么该约束条件取严格等式;反之如果约束条件取严格不等式,那么对应的对偶变量一定为零。也即:
{ y i ∗ ( ∑ j = 1 n a i j x j − b i ) = 0 ( i = 1 , 2 , … , m ) x j ∗ ( ∑ i = 1 m a i j y i − c j ) = 0 ( j = 1 , 2 , … , n ) \left\{\begin{array}{l} y_i *\left(\sum_{j=1}^n a_{i j} x_j-b_i\right)=0(i=1,2, \ldots, m) \\ x_j *\left(\sum_{i=1}^m a_{i j} y_i-c_j\right)=0(j=1,2, \ldots, n) \end{array}\right. {yi∗(∑j=1naijxj−bi)=0(i=1,2,…,m)xj∗(∑i=1maijyi−cj)=0(j=1,2,…,n)
应用:由原/对偶问题最优解求对偶/原问题最优解
相关文章:

对偶问题的基本性质
写于:2024年1月3日晚 修改于: 原规划与对偶规划 原规划对偶规划 max z C T X s.t. { A X ≤ b , 其中 X ( m ∗ 1 ) X ≥ 0 \begin{aligned} & \max \mathrm{z}\mathbf{C}^T \mathbf{X} \\ & \text { s.t. }\left\{\begin{array}{l}\mat…...

Google Chrome 现在会在后台扫描泄露的密码
谷歌表示,Chrome 安全检查功能将在后台运行,检查网络浏览器中保存的密码是否已被泄露。 如果桌面用户正在使用标记为危险的扩展程序(从 Chrome Web Store 中删除)、最新的 Chrome 版本,或者如果启用安全浏览来阻止 Go…...
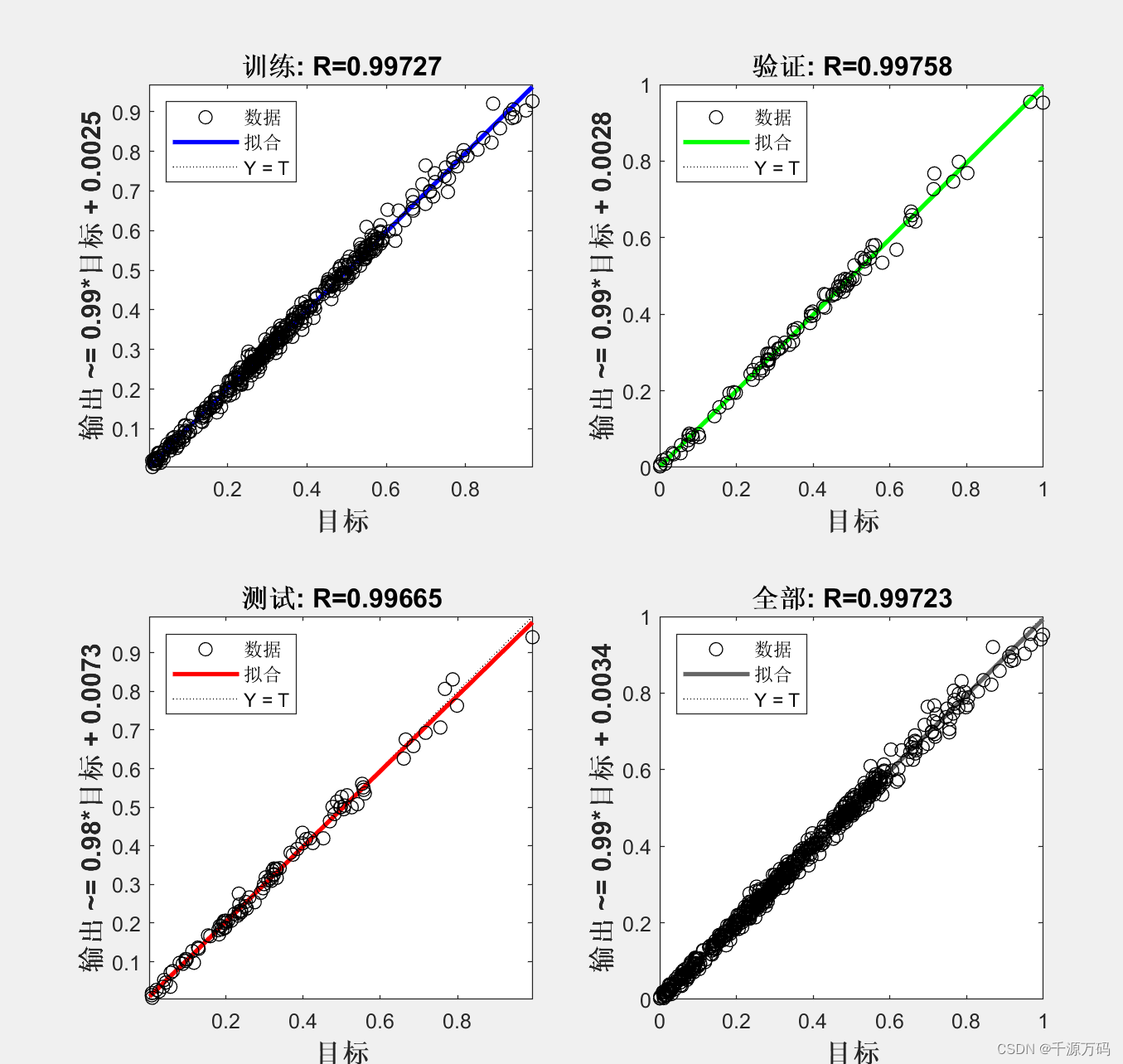
【Matlab】PSO-BP 基于粒子群算法优化BP神经网络的数据时序预测(附代码)
资源下载: https://download.csdn.net/download/vvoennvv/88689096 目录 【Matlab】BP 神经网络时序预测算法 【Matlab】CNN卷积神经网络时序预测算法 【Matlab】ELM极限学习机时序预测算法 【Matlab】基于遗传算法优化BP神经网络 (GA-BP)的数据时序预测 【Mat…...

Linux 485驱动通信异常
背景 前段时间接到一个项目,要求用主控用485和MCU通信。将代码调试好之后,验证没问题就发给测试了。测试测的也没问题。 但是,到设备量产时,发现有几台设备功能异常。将设备拿回来排查,发现是485通信有问题ÿ…...

mybatis配置与标签大全
文章目录 mybatis配置与标签大全mybatis的配置属性(properties)设置(settings)类型别名(typeAliases)类型处理器(typeHandlers)对象工厂(objectFactory)插件&…...
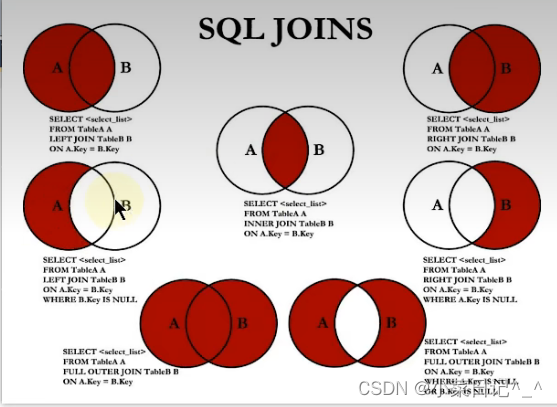
Mysql的基本用法(上)非常详细、快速上手
上篇结束了java基础,本篇主要对Mysql中的一些常用的方法进行了总结,主要对查询方法进行了讲解,包括重要的多表查询用到的内连接和外连接等,以下代码可以直接复制到可视化软件中,方便阅读以及练习; SELECT *…...
)
使用Vite创建React + TypeScript(node版本为16.17.0,含资源下载)
PC端 安装指令: npm create vitelatest react-ts-pro -- --template react-tsVite是一个框架无关的前端工具链,可以快速的生成一个React TS的开发环境,并且可以提供快速的开发体验说明: 1. npm create vitelatest固定写法&#…...

Springboot集成RabbitMq二
接上一篇:Springboot集成RabbitMq一-CSDN博客 1、搭建项目-消费者 与之前一样 2、创建配置类 package com.wym.rabbitmqconsumer.utils;import org.springframework.amqp.core.Binding; import org.springframework.amqp.core.BindingBuilder; import org.spring…...

机器学习笔记 - 基于Python的不平衡数据的欠采样技术
一、简述 随着从不同的来源生成和捕获大量数据。尽管信息量巨大,但它往往反映了现实世界现象的不平衡分布。数据不平衡的问题不仅仅是统计上的挑战,它对数据驱动模型的准确性和可靠性具有深远的影响。 以金融行业欺诈检测为例。尽管我们希望避免欺诈,因为其具有高度破坏性,…...

facebook广告的基础知识
Facebook广告是在Facebook、Instagram、Audience Network等与Facebook相关的SNS和服务上投放的广告。以下是关于Facebook广告的基础知识: 广告类型: 静态图片广告:主要通过Facebook的新闻提要投放的图片广告,可以张贴产品和服务…...

java常见面试题:什么是异常?Java中的异常有哪些分类?
异常是一个汉语词语,读音为y chng,指非正常的;不同于平常的;非常。在Java中,异常(Exception)是程序在运行过程中出现的不正常情况,例如除以零、数组越界等。异常分为两大类ÿ…...
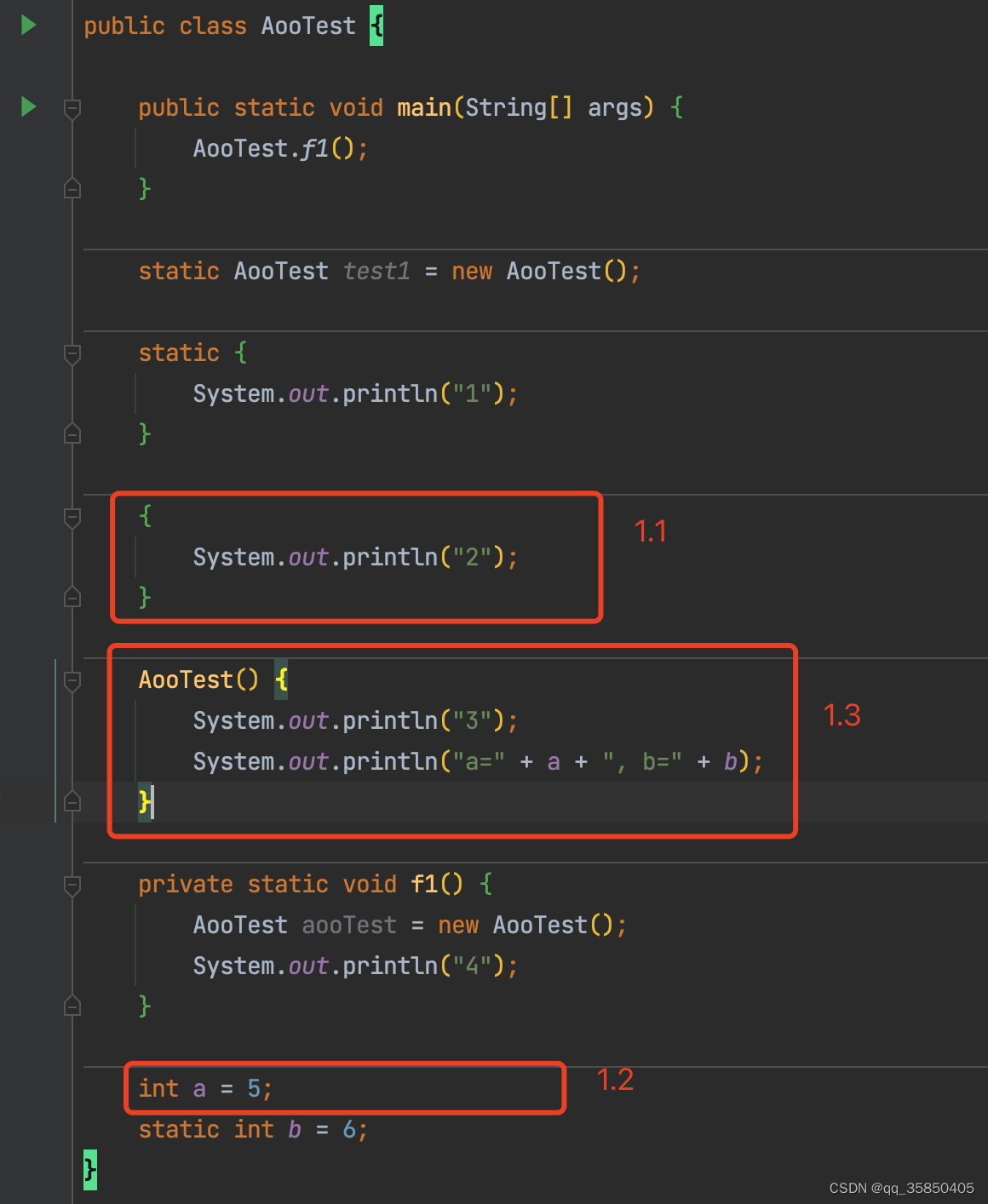
类的加载顺序问题-demo展示
面试的的时候经常会被问到包含静态代码块、实例代码块和构造器等代码结构的加载顺序问题,下面借用一个面试题,回顾一下类的代码加载顺序。 public class AooTest {public static void main(String[] args) {AooTest.f1();}static AooTest test1 new Ao…...

[蓝桥杯2020国赛]答疑
答疑 题目描述 有 n 位同学同时找老师答疑。每位同学都预先估计了自己答疑的时间。 老师可以安排答疑的顺序,同学们要依次进入老师办公室答疑。 一位同学答疑的过程如下: 首先进入办公室,编号为 i 的同学需要 si 毫秒的时间。然后同学问…...

【AIGC表情prompt】提示词练习技巧
表情类提示词练习技巧 医疗机器人,男人笑脸景深,数据,座标,12k,c4d渲染,高分辨率,,暖色调,高清对比 医疗机器人,男人微笑,景深,数据,座标…...
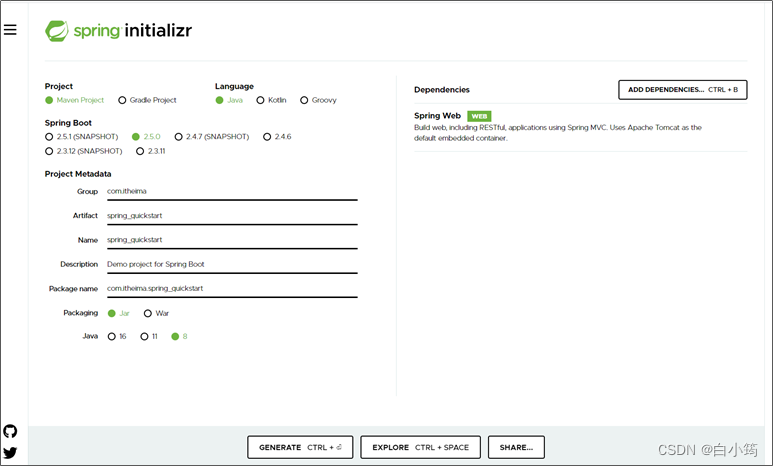
SpringBoot项目的三种创建方式
手动创建方式: ①:新建maven项目 ②:引入依赖 <parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><version>2.3.10.RELEASE</version>&l…...
【docker实战】01 Linux上docker的安装
Docker CE是免费的Docker产品的新名称,Docker CE包含了完整的Docker平台,非常适合开发人员和运维团队构建容器APP。 Ubuntu 14.04/16.04(使用 apt-get 进行安装) # step 1: 安装必要的一些系统工具 sudo apt-get update sudo ap…...
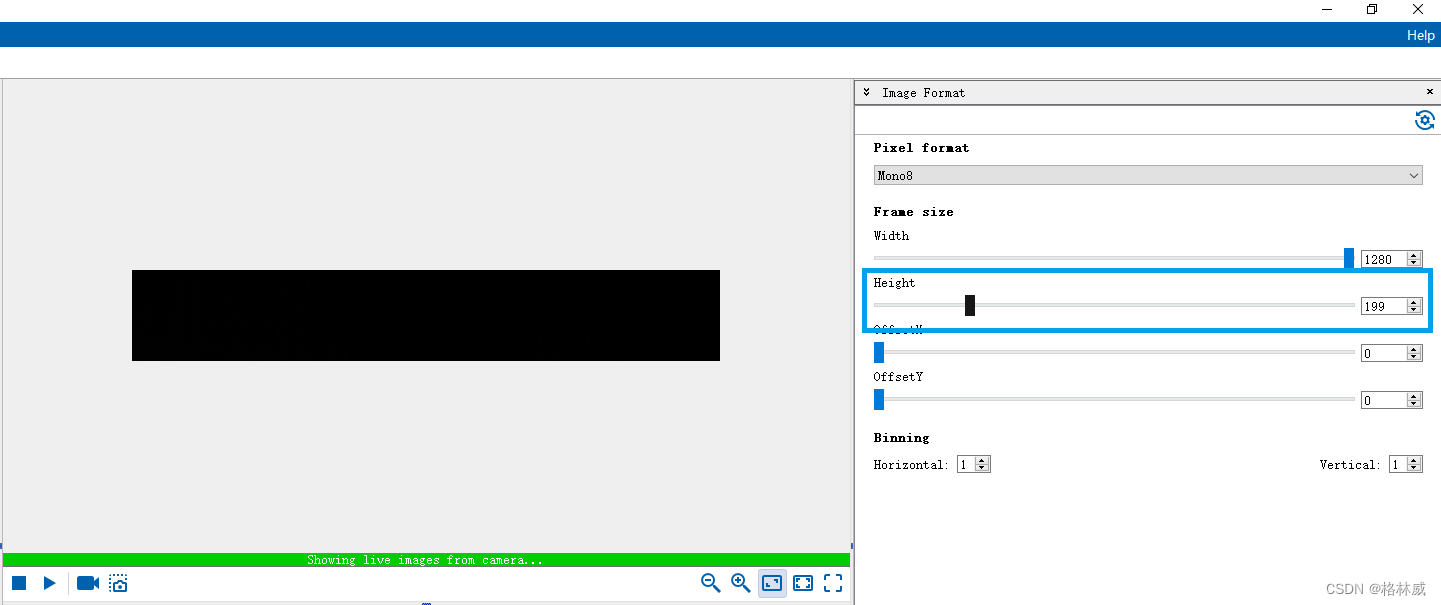
Baumer工业相机堡盟工业相机如何通过NEOAPI SDK设置相机的图像剪切(ROI)功能(C#)
Baumer工业相机堡盟工业相机如何通过NEOAPI SDK设置相机的图像剪切(ROI)功能(C#) Baumer工业相机Baumer工业相机的图像剪切(ROI)功能的技术背景CameraExplorer如何使用图像剪切(ROI)…...

软件测试之安全测试
一、测试范围 管理系统:url、登录框、搜索框、输入框、文件上传、文件下载 客户端:搜索框、输入框、文件上传、系统功能 二、测试点 密码安全 XSS注入 SQL注入 操作越权 上传安全 下载安全 三、工具 fiddler sqlmap 同时,在这我为…...

【华为OD机试真题2023CD卷 JAVAJS】会议室占用时间
华为OD2023(C&D卷)机试题库全覆盖,刷题指南点这里 会议室占用时间 时间限制:1s 空间限制:256MB 限定语言:不限 题目描述: 现有若干个会议,所有会议共享一个会议室,用数组表示每个会议的开始时间和结束时间,格式:[[会议1开始时间,会议1结束时间], [会议2开始时间…...

UR5机器人的旋转向量转换到四元数,再从四元数转换到旋转向量python代码
能够通过接口获得UR5机器人末端在基坐标系下的位姿,姿态表示方法是用旋转向量表示的,一般会涉及到四元数和旋转向量之间的转换。 1、方法一 import numpy as np from pytransform3d import rotations as pr import copy # 输入旋转向量 quaternion2 n…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

从实验室到产业:IndexTTS 在六大核心场景的落地实践
一、内容创作:重构数字内容生产范式 在短视频创作领域,IndexTTS 的语音克隆技术彻底改变了配音流程。B 站 UP 主通过 5 秒参考音频即可克隆出郭老师音色,生成的 “各位吴彦祖们大家好” 语音相似度达 97%,单条视频播放量突破百万…...

结构化文件管理实战:实现目录自动创建与归类
手动操作容易因疲劳或疏忽导致命名错误、路径混乱等问题,进而引发后续程序异常。使用工具进行标准化操作,能有效降低出错概率。 需要快速整理大量文件的技术用户而言,这款工具提供了一种轻便高效的解决方案。程序体积仅有 156KB,…...
