第十四届蓝桥杯模拟赛(第三期)——C语言版
1.找最小数
问题描述:
请找到一个大于 2022 的最小数,这个数转换成十六进制之后,所有的数位(不含前导 0)都为字母(A 到 F)。
请将这个数的十进制形式作为答案提交。
#include <stdio.h>
int main(){int i;char ch;for(i=2023;;i++){int temp=i;while(temp!=0){ch=temp%16+'0';if(ch<='9')break;temp=temp/16;}if(temp==0)break;}printf("%d",i);return 0;
}
2730
2.求列名
问题描述:
在 Excel 中,列的名称使用英文字母的组合。前 26 列用一个字母,依次为 A 到 Z,接下来 26*26 列使用两个字母的组合,依次为 AA 到 ZZ。
请问第 2022 列的名称是什么?
#include <stdio.h>
#include <math.h>
int main(){int i=2022,j,sum=0,n;for(j=1;;j++){sum+=pow(26,j);if(sum>=i)break;}for(j-=1;j>=0;j--){n=i/pow(26,j);i-=n*pow(26,j);printf("%c",'A'+(n-1));}return 0;
}
BYT
3.求日期数
问题描述:
对于一个日期,我们可以计算出年份的各个数位上的数字之和,也可以分别计算月和日的各位数字之和。请问从 1900 年 1 月 1 日至 9999 年 12 月 31 日,总共有多少天,年份的数位数字之和等于月的数位数字之和加日的数位数字之和。例如,2022年11月13日满足要求,因为 2+0+2+2=(1+1)+(1+3) 。
请提交满足条件的日期的总数量。
#include <stdio.h>
#include <math.h>
int main(){int count=0;int y_sum=0,m_sum=0,d_sum=0;int y,m,d;for(y=1900;y<=9999;y++){int temp1=y;y_sum=0;while(temp1>0){y_sum+=temp1%10;temp1/=10;}for(m=1;m<=12;m++){int temp2=m;m_sum=0;while(temp2>0){m_sum+=temp2%10;temp2/=10;}for(d=1;d<=31;d++){if(d==31&&(m==2||m==4||m==6||m==9||m==11))continue;if(((y%4==0&&y%100!=0)||(y%400==0))&&m==2&&d>29)break;else if(!((y%4==0&&y%100!=0)||(y%400==0))&&m==2&&d>28)break;int temp3=d;d_sum=0;while(temp3>0){d_sum+=temp3%10;temp3/=10;}if(y_sum==(m_sum+d_sum)){count++;
// printf(" %d %d 年 %d 月 %d 日\n",count,y,m,d);
// if(count%100==0){
// getchar();
// }d+=8;}else if(y_sum>(m_sum+d_sum)){d+=(y_sum-(m_sum+d_sum)-1);}}}}printf("%d\n",count);return 0;
}
70910
4.取数
问题描述:
小蓝有 30 个数,分别为:99, 22, 51, 63, 72, 61, 20, 88, 40, 21, 63, 30, 11, 18, 99, 12, 93, 16, 7, 53, 64, 9, 28, 84, 34, 96, 52, 82, 51, 77 。
小蓝可以在这些数中取出两个序号不同的数,共有 30*29/2=435 种取法。
请问这 435 种取法中,有多少种取法取出的两个数的乘积大于等于 2022 。
#include <stdio.h>
int main(){int num[31]={99,22,51,63,72,61,20,88,40,21,63,30,11,18,99,12,93,16,7,53,64,9,28,84,34,96,52,82,51,77};int count=0;for(int i=0;i<30;i++){for(int j=i+1;j<30;j++){if(num[i]*num[j]>=2022){count++;}}}printf("%d",count);return 0;
}
189
5.最大连通分块
问题描述:
小蓝有一个 30 行 60 列的数字矩阵,矩阵中的每个数都是 0 或 1 。
如果从一个标为 1 的位置可以通过上下左右走到另一个标为 1 的位置,则称两个位置连通。与某一个标为 1 的位置连通的所有位置(包括自己)组成一个连通分块。
请问矩阵中最大的连通分块有多大?
6.n天后周几
输入格式
输入第一行包含一个整数 w,表示给定的天是一周中的哪天,w 为 1 到 6 分别表示周一到周六,w 为 7 表示周日。第二行包含一个整数 n。
输出格式
输出一行包含一个整数,表示 n 天后是一周中的哪天,1 到 6 分别表示周一到周六,7 表示周日。。
评测用例规模与约定
对于所有评测用例,1 <= n <= 1000000。
#include <stdio.h>
#include <stdlib.h>int main(){int w;scanf("%d",&w);int n;scanf("%d",&n);if(w+n<=7)printf("%d",w+n);else{n-=(7-w);n%=7;printf("%d",n);}return 0;
}
样例输入
6
10
样例输出
2
7.信号塔信号覆盖点数
问题描述
小蓝负责一块区域的信号塔安装,整块区域是一个长方形区域,建立坐标轴后,西南角坐标为 (0, 0), 东南角坐标为 (W, 0), 西北角坐标为 (0, H), 东北角坐标为 (W, H)。其中 W, H 都是整数。
他在 n 个位置设置了信号塔,每个信号塔可以覆盖以自己为圆心,半径为 R 的圆形(包括边缘)。
为了对信号覆盖的情况进行检查,小蓝打算在区域内的所有横纵坐标为整数的点进行测试,检查信号状态。其中横坐标范围为 0 到 W,纵坐标范围为 0 到 H,总共测试 (W+1) * (H+1) 个点。
给定信号塔的位置,请问这 (W+1)*(H+1) 个点中有多少个点被信号覆盖。
输入格式
输入第一行包含四个整数 W, H, n, R,相邻整数之间使用一个空格分隔。
接下来 n 行,每行包含两个整数 x, y,表示一个信号塔的坐标。信号塔可能重合,表示两个信号发射器装在了同一个位置。
输出格式
输出一行包含一个整数,表示答案。
评测用例规模与约定
对于所有评测用例,1 <= n <= 100,每个单词的长度不超过 100。
#include <stdio.h>
#include <math.h>int main(){int W,H,n,r,count=0;int x[101]={0},y[101]={0};scanf("%d %d %d %d",&W,&H,&n,&r);for(int i=0;i<n;i++){scanf("%d %d",&x[i],&y[i]);}for(int i=0;i<=W;i++){for(int j=0;j<H;j++){for(int k=0;k<n;k++){if(sqrt(pow((i-x[k]),2)+pow((j-y[k]),2))<=r){count++;break;}}}}printf("%d",count);return 0;
}
样例输入
10 10 2 5
0 0
7 0
样例输出
57
8.清理水草
问题描述
小蓝有一个 n * m 大小的矩形水域,小蓝将这个水域划分为 n 行 m 列,行数从 1 到 n 标号,列数从 1 到 m 标号。每行和每列的宽度都是单位 1 。
现在,这个水域长满了水草,小蓝要清理水草。
每次,小蓝可以清理一块矩形的区域,从第 r1 行(含)到第 r2 行(含)的第 c1 列(含)到 c2 列(含)。
经过一段时间清理后,请问还有多少地方没有被清理过。
输入格式
输入第一行包含两个整数 n, m,用一个空格分隔。
第二行包含一个整数 t ,表示清理的次数。
接下来 t 行,每行四个整数 r1, c1, r2, c2,相邻整数之间用一个空格分隔,表示一次清理。请注意输入的顺序。
输出格式
输出一行包含一个整数,表示没有被清理过的面积。
评测用例规模与约定
对于所有评测用例,1 <= r1 <= r2 <= n <= 100, 1 <= c1 <= c2 <= m <= 100, 0 <= t <= 100。
#include <stdio.h>
#include <math.h>int main(){int m,n,r1[101],r2[101],c1[101],c2[101];scanf("%d %d",&n,&m);int t,count=0;scanf("%d",&t);for(int i=1;i<=t;i++){scanf("%d %d %d %d",&r1[i],&c1[i],&r2[i],&c2[i]);}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){for(int k=1;k<=t;k++){if(i>=r1[k]&&i<=r2[k]){if((i>=r1[k])&&(i<=r2[k])&&(j>=c1[k])&&(j<=c2[k])){count++;break;}}}}}printf("%d",m*n-count);return 0;
}
样例输入
2 3
2
1 1 1 3
1 2 2 2
样例输出
2
样例输入
30 20
2
5 5 10 15
6 7 15 9
样例输出
519
9.滑行距离
问题描述
小蓝准备在一个空旷的场地里面滑行,这个场地的高度不一,小蓝用一个 n 行 m 列的矩阵来表示场地,矩阵中的数值表示场地的高度。
如果小蓝在某个位置,而他上、下、左、右中有一个位置的高度(严格)低于当前的高度,小蓝就可以滑过去,滑动距离为 1 。
如果小蓝在某个位置,而他上、下、左、右中所有位置的高度都大于等于当前的高度,小蓝的滑行就结束了。
小蓝不能滑出矩阵所表示的场地。
小蓝可以任意选择一个位置开始滑行,请问小蓝最多能滑行多远距离。
输入格式
输入第一行包含两个整数 n, m,用一个空格分隔。
接下来 n 行,每行包含 m 个整数,相邻整数之间用一个空格分隔,依次表示每个位置的高度。
输出格式
输出一行包含一个整数,表示答案。
评测用例规模与约定
对于 30% 评测用例,1 <= n <= 20,1 <= m <= 20,0 <= 高度 <= 100。
对于所有评测用例,1 <= n <= 100,1 <= m <= 100,0 <= 高度 <= 10000。
10.求最小值
问题描述
小蓝有一个序列 a[1], a[2], …, a[n]。
给定一个正整数 k,请问对于每一个 1 到 n 之间的序号 i,a[i-k], a[i-k+1], …, a[i+k] 这 2k+1 个数中的最小值是多少?当某个下标超过 1 到 n 的范围时,数不存在,求最小值时只取存在的那些值。
输入格式
输入的第一行包含一整数 n。
第二行包含 n 个整数,分别表示 a[1], a[2], …, a[n]。
第三行包含一个整数 k 。
输出格式
输出一行,包含 n 个整数,分别表示对于每个序号求得的最小值。
评测用例规模与约定
对于 30% 的评测用例,1 <= n <= 1000,1 <= a[i] <= 1000。
对于 50% 的评测用例,1 <= n <= 10000,1 <= a[i] <= 10000。
对于所有评测用例,1 <= n <= 1000000,1 <= a[i] <=1000000。
相关文章:
——C语言版)
第十四届蓝桥杯模拟赛(第三期)——C语言版
1.找最小数 问题描述: 请找到一个大于 2022 的最小数,这个数转换成十六进制之后,所有的数位(不含前导 0)都为字母(A 到 F)。 请将这个数的十进制形式作为答案提交。 #include <stdio.h> int main(…...
Flutter Button 实例
大家好,我是 17。 在上篇文章 使用 Flutter Button 介绍了如何修改 button 的样式,本文来具体实践一下。 本文列举一些常用的 button 效果,以便在用到的时候方便使用。因为 ElevatedButton 最常用,所以大多以 ElevatedButton 举…...
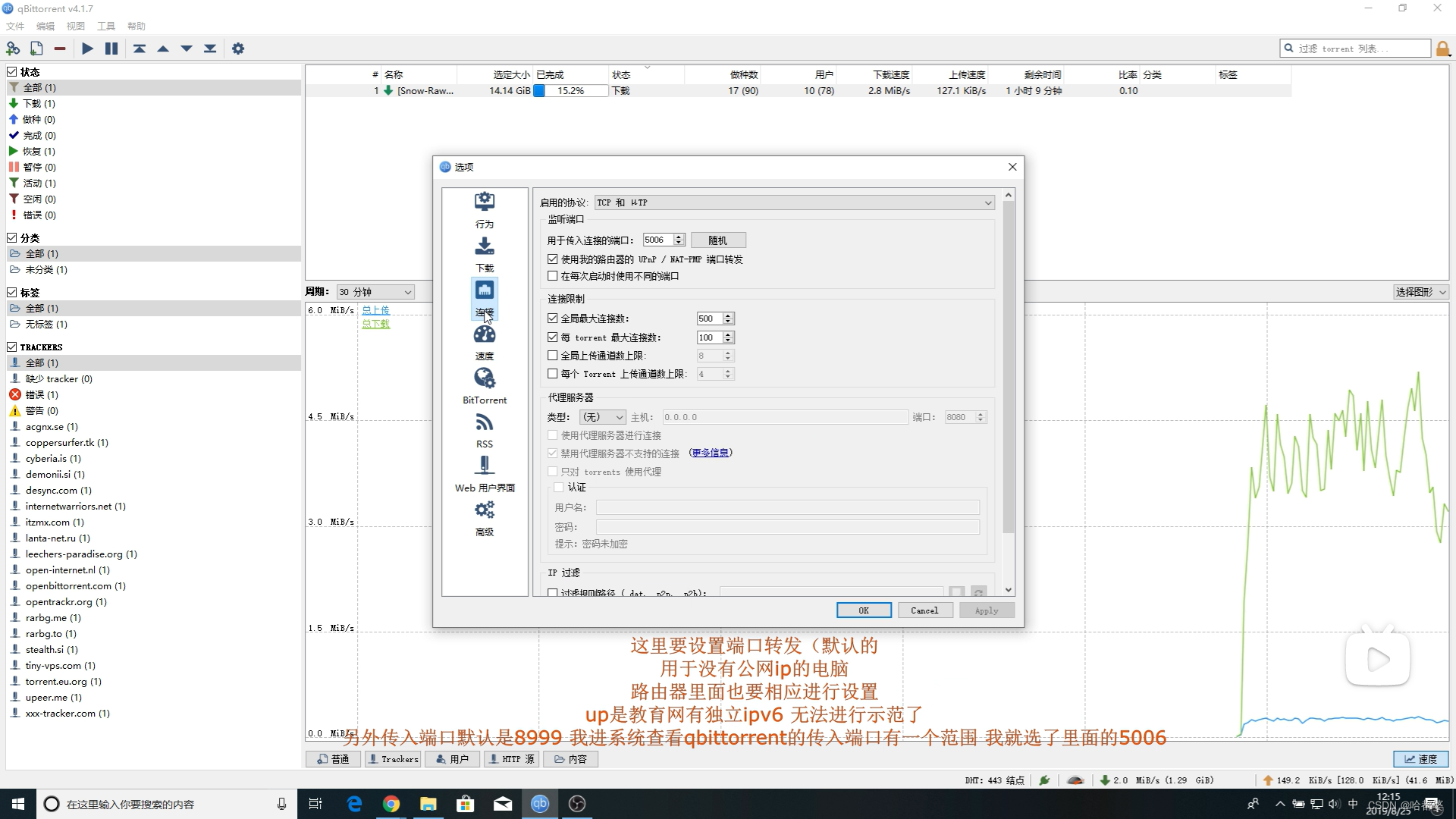
好玩的docker项目,盒子刷的海思nas,挂载外接硬盘。qb种子
玩法思路(5条消息) 群晖qb下载,tr辅种_屿兮的博客-CSDN博客_群晖辅种qbittorrent简介及设置_哔哩哔哩_bilibiliqb下载器下载Transmission最好用的BT(PT)下载神器/超简单上手教你在NAS轻松部署/告别简陋三步让你升级全中文最新Web界面(BT下载/PT下载/NAS/…...

RabbitMQ的使用
1.初识MQ1.1.同步和异步通讯微服务间通讯有同步和异步两种方式:同步通讯:就像打电话,需要实时响应。异步通讯:就像发邮件,不需要马上回复。两种方式各有优劣,打电话可以立即得到响应,但是你却不…...
Selenium如何隐藏浏览器页面?
Selenium隐藏浏览器页面 背景 在工作,学习中,我们常常会使用selenium来获取网页上的数据,编完完整程序之后,实现真正意义上的自动化获取,此时我们会发现在运行中往往会弹出浏览器页面,在调试过程中&…...
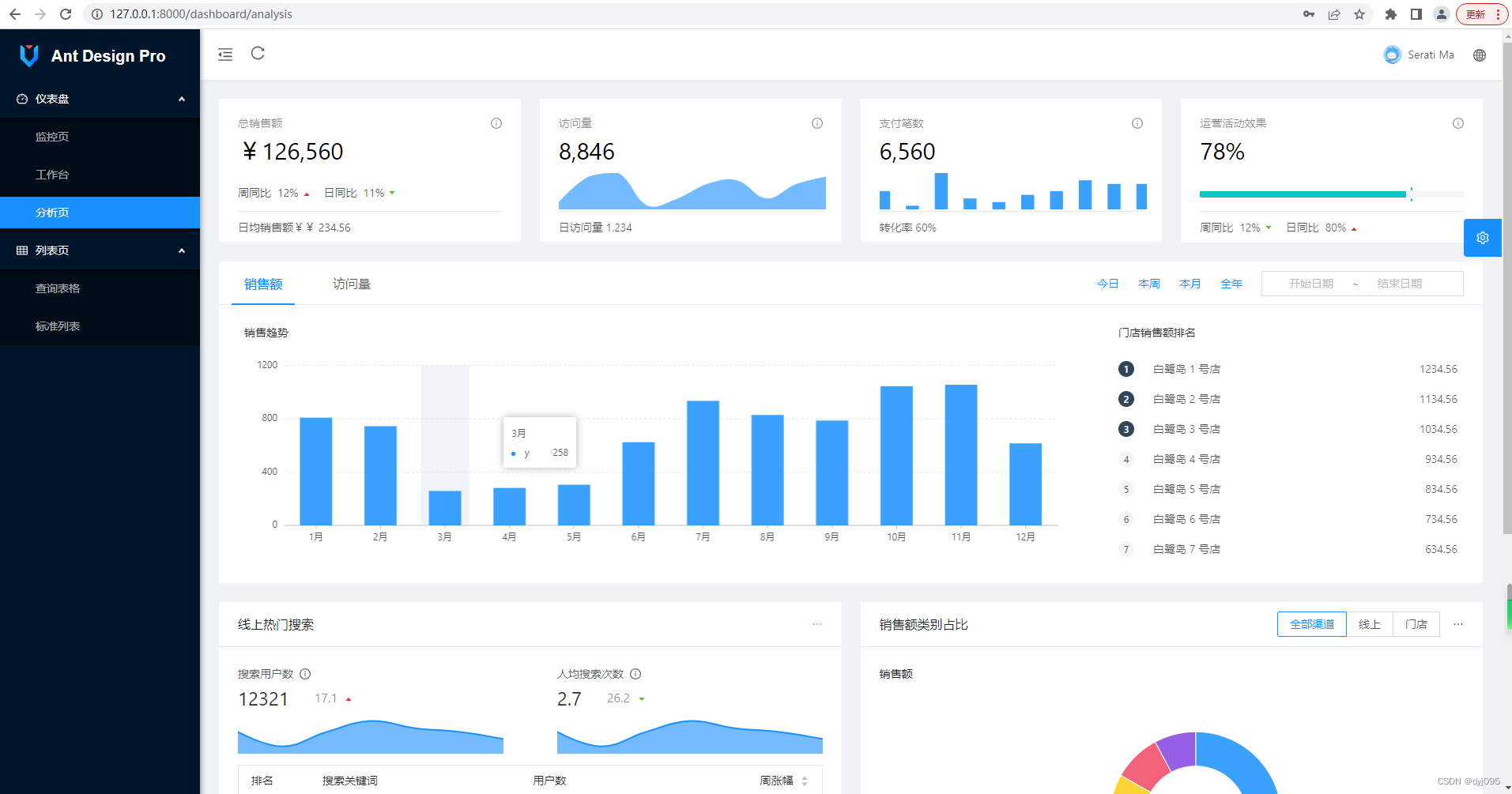
基于Ant DesignPro Vue实现通过SpringBoot后台加载自定义菜单- 前后端分离
基于Ant DesignPro Vue实现通过SpringBoot后台加载自定义菜单- 前后端分离 本文想基于Ant DesignPro Vue构建的前端SpringBoot实现的后端接口服务,实现前后端分离开发和独立运行,业务场景是登录认证,认证成功后返回该用户相应权限范围内可见的…...
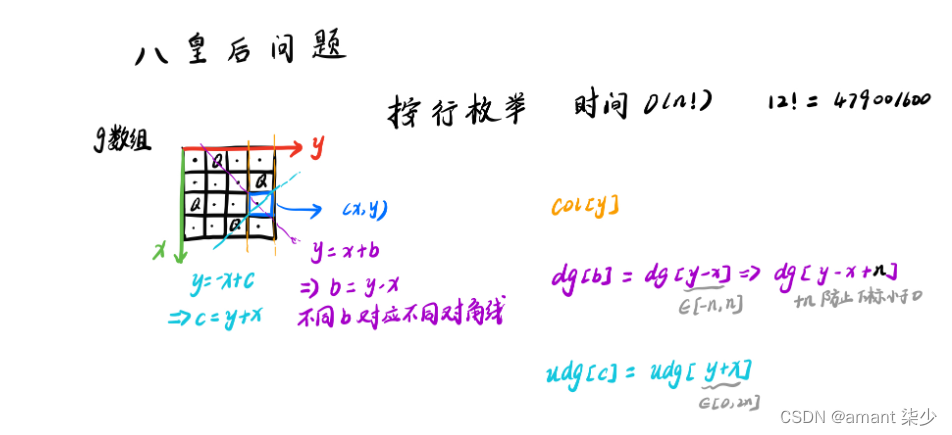
Acwing---843. n-皇后问题
n-皇后问题1.题目2.基本思想3.代码实现1.题目 n−皇后问题是指将 n 个皇后放在 nn 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。 现在给定整数 n,请你输出所有的满足条件的棋子摆法。 …...

彻底搞清楚内存泄漏的原因,如何避免内存泄漏,如何定位内存泄漏
作为C/C开发人员,内存泄漏是最容易遇到的问题之一,这是由C/C语言的特性引起的。C/C语言与其他语言不同,需要开发者去申请和释放内存,即需要开发者去管理内存,如果内存使用不当,就容易造成段错误(segment fa…...
自动驾驶目标检测项目实战——基于深度学习框架yolov的交通标志检测
自动驾驶目标检测项目实战——基于深度学习框架yolov的交通标志检测 目前目标检测算法有很多,流行的就有faster-rnn和yolov,本文使用了几年前的yolov3框架进行训练,效果还是很好,当然也可以使用更高版本的Yolov进行实战。本代码使…...

flink兼容性验证
flink介绍:https://blog.csdn.net/weixin_43563705/article/details/107604693 一、安装启动 安装flink及其依赖 yum install java-1.8.0-openjdk curl tar mkdir -p /usr/local/flink wget https://mirrors.aliyun.com/apache/flink/flink-1.16.1/flink-1.16.1-bi…...

智慧工厂数字孪生可视化监测系统有效提升厂区安全管控效力
我国制造业正处于产业升级的关键时期,基于数据进行生产策略制定与管理是大势所趋,而数据可视化以更直观的方式成为数据分析传递信息的重要工具。 深圳华锐视点通过三维可视化手段对工厂各类设备进行三维建模,真实复现设备设施外观、结构、运转…...

c++中基本类型详细解释外加基本运算规则
👀👀#c中包括算数类型和空类型。 类型含义wchat_t宽字符bool布尔类型char字符chat16_tunicode字符chat_32unicode字符short短整型int整形long长整型longlong长整型float单精度浮点型double双精度浮点型longdouble扩展精度浮点型 👀…...

扬帆优配“机器人+”方案加码产业发展,这些股有望高增长
“机器人”发明新需求,2022年中国机器人市场规模约为174亿美元。 美国时刻3月1日,特斯拉在得克萨斯州超级工厂举办投资者日活动,展示了人形机器人Optimus的视频,更夸大的是,视频中的机器人好像在制作另一个机器人&…...
推送投票制作微信推送里投票制作教程在线投票活动制作
近些年来,第三方的微信投票制作平台如雨后春笋般络绎不绝。随着手机的互联网的发展及微信开放平台各项基于手机能力的开放,更多人选择微信投票小程序平台,因为它有非常大的优势。1.它比起微信公众号自带的投票系统、传统的H5投票系统有可以图…...
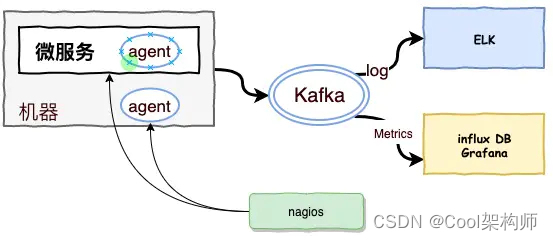
【架构师】跟我一起学架构——微服务分层监控
博客昵称:架构师Cool 最喜欢的座右铭:一以贯之的努力,不得懈怠的人生。 作者简介:一名Coder,软件设计师/鸿蒙高级工程师认证,在备战高级架构师/系统分析师,欢迎关注小弟! 博主小留言…...
Linux:https静态网站搭建案例
目录介绍httpshttps通信过程例介绍https 整个实验是在http实验基础上进行的 因为http协议在传输的时候采用的是明文传输,有安全隐患,所以出现了https(安全套接字层超文本传输协议) HTTPS并不是一个新协议, 而是HTTP…...

前端css整理
如何水平垂直居中一个盒子? 1.已知高度:子盒子设置 display: inline-block; 父盒子设置 line-height 等于高度实现垂直居中;使用 text-align:center实现水平居中 2.父盒子 display:flex; align-items:center;justify-content:center; 3.定位&…...

混凝土搅拌站远程监控解决方案
一、项目背景 随着大规模的基础设施建设,对混凝土搅拌设备的需求量日益增加,对其技术指标的要求也日益提高,其技术性能将直接关系到工程的质量和使用寿命。而混凝土生产的质量是在生产过程中形成的,而非最终强度的检测。混凝土生…...

Spark SQL 学习总结
文章目录(一)Spark SQL(二)SParkSession(三)DataFrame常见算子操作(四)DataFrame的sql操作(五)RDD转换为DataFrame(1)反射方式&#x…...

深度学习 - 37.TF x Keras Deep Cross Network DCN 实现
目录 一.引言 二.模型简介 1.Embedding and stacking layer 2.Cross Network 2.1 模型架构分析 2.2 计算逻辑...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

Qt的学习(一)
1.什么是Qt Qt特指用来进行桌面应用开发(电脑上写的程序)涉及到的一套技术Qt无法开发网页前端,也不能开发移动应用。 客户端开发的重要任务:编写和用户交互的界面。一般来说和用户交互的界面,有两种典型风格&…...

如何把工业通信协议转换成http websocket
1.现状 工业通信协议多数工作在边缘设备上,比如:PLC、IOT盒子等。上层业务系统需要根据不同的工业协议做对应开发,当设备上用的是modbus从站时,采集设备数据需要开发modbus主站;当设备上用的是西门子PN协议时…...

深度解析云存储:概念、架构与应用实践
在数据爆炸式增长的时代,传统本地存储因容量限制、管理复杂等问题,已难以满足企业和个人的需求。云存储凭借灵活扩展、便捷访问等特性,成为数据存储领域的主流解决方案。从个人照片备份到企业核心数据管理,云存储正重塑数据存储与…...
