内坐标转换计算
前言
化学这边的库太多了。
cs这边的库太少了。
去看化学的库太累了。
写一个简单的实现思路,让cs的人能看懂。
向量夹角的范围
[0, pi)
这是合理的。
因为两个向量只能构成一个平面系统,平面系统内的夹角不能超过pi。
二面角的范围
涉及二面角,说明坐标空间至少是E(3),可以更高维。
严格定义
严格意义上,二面角的定义是2个半平面的夹角。
在严格定义下,二面角的取值范围必然是 [0, pi)。
但上面这个定义显然不是我们cs人喜欢的。
因为在E(3)中,如果使用[0,pi)的二面角定义坐标系统,则会有手性问题
例如:
下图中2个D都符合要求。
(图略)
本质上是因为,与某一半平面A的夹角为 [ 0 , π ) [0, \pi) [0,π) 的半平面有2个。
需要一个额外的sign来指示,point处于这两个半平面中的哪一个。
使用 [ − π , π ) [-\pi, \pi) [−π,π)的广义二面角,可以唯一确定一个三维空间内的相对位置。
这个广义二面角事实上等价于 旋转角 。
旋转角就是采用四元数计算的,范围也是 [ 0 , 2 π ) [0, 2\pi) [0,2π) 。
两个向量的旋转角,是指从向量p1开始,逆时针旋转,转到向量p2时,所转过的角度, 范围是 0 ~ 360度
定义
给定一个有序列(ordered sequence) = [A,B,C,D]。
约定 A,B,C,D 构成的广义二面角为向量 B A ⃗ , C B ⃗ , D C ⃗ \vec{BA}, \vec{CB}, \vec{DC} BA,CB,DC 构成的2个平面法向量
n ⃗ 1 = n ⃗ C B A \vec{n}_1=\vec{n}_{CBA} n1=nCBA 与 n ⃗ 2 = n ⃗ D C B \vec{n}_2=\vec{n}_{DCB} n2=nDCB之间, n ⃗ 2 \vec{n}_{2} n2 逆时针转到 n ⃗ 1 \vec{n}_{1} n1 的旋转角。
(后一个面的法向量转到前一个面)
可以这样想,在E3空间中,给定2个向量,用右手定则可以得到他们叉乘的法向量。
从该法向量逆向往正向看去,就能建立一个2D平面坐标系。
在该2D平面坐标系上,v2逆时针旋转到v1的夹角是唯一确定的,取值[0,2pi)。
https://zhuanlan.zhihu.com/p/45404840
笛卡尔坐标转内坐标
Convention

示例输入:
import torchcart_coord = torch.tensor([[1,0,0],[0,0,0],[0,2,0],[0,0,2]])
我们期望得到的内坐标
tensor([ 1.0000, 2.0000, 2.8284, 1.5708, 0.7854, -1.5708])
转成易读形式:
1.0000, 2.0000, 2.8284, pi/2, pi/4, -pi/2
键角[0, pi) 。
对最后一个元素,即广义二面角,需要做说明。
在该特殊例子中,
后一个面DCB的法向量是 B A ⃗ \vec{BA} BA (右手定则),
前一个面CBA的法向量是 D B ⃗ \vec{DB} DB (右手定则)。
后者逆时针转到前者的角度是 -pi/2。 ( 取值范围 [-pi, pi) )。
进一步地,我们可以证明,在general case中,
后一个面按右手定则得到的法向量,等于 B A ⃗ \vec{BA} BA 垂直于 C B ⃗ \vec{CB} CB的分量。
前一个面按右手定则得到的法向量,等于 D C ⃗ \vec{DC} DC垂直于 C B ⃗ \vec{CB} CB的分量。
于是二面角 (D,C,B,A)本质上就是 B A ⃗ \vec{BA} BA 与 D C ⃗ \vec{DC} DC 在 C B ⃗ \vec{CB} CB垂直平面上的分量之间的夹角。
理解这个性质对下面的内容会有帮助。
内坐标转笛卡尔算法
前置知识: 向量绕任意轴旋转矩阵
https://zhuanlan.zhihu.com/p/380237903
https://blog.csdn.net/FreeSouthS/article/details/112576370
https://zhuanlan.zhihu.com/p/56587491
Rodrigues’旋转公式
设旋转轴 n ⃗ = ( n x , n y , n z ) \vec{n}=(n_x,n_y,n_z) n=(nx,ny,nz) 。
写出 n ⃗ \vec{n} n的叉乘矩阵:
N = [ 0 , − n z , n y n z , 0 , − n x − n y , n x , 0 ] N=\left[\begin{array}{ccc}0, & -n_z, & n_y \\ n_z, & 0, & -n_x \\ -n_y, & n_x, & 0\end{array}\right] N= 0,nz,−ny,−nz,0,nx,ny−nx0 。
于是叉乘:
n × p = [ 0 , − n z , n y n z , 0 , − n x − n y , n x , 0 ] p = N p \mathbf{n} \times \mathbf{p}=\left[\begin{array}{ccc}0, & -n_z, & n_y \\ n_z, & 0, & -n_x \\ -n_y, & n_x, & 0\end{array}\right] \mathbf{p}=\mathbf{N} \mathbf{p} n×p= 0,nz,−ny,−nz,0,nx,ny−nx0 p=Np
于是绕 n ⃗ \vec{n} n的旋转矩阵为:
R = I + sin ( θ ) N + ( 1 − cos ( θ ) ) N 2 \mathbf{R}=\mathbf{I}+\sin (\theta) \mathbf{N}+(1-\cos (\theta)) \mathbf{N}^2 R=I+sin(θ)N+(1−cos(θ))N2
旋转后向量
p ⃗ ′ = R p ⃗ \vec{p}'=\mathbf{R}\vec{p} p′=Rp。
或者用向量形式
p ′ = p ⊥ ′ + p ∥ ′ = cos ( θ ) p ⊥ + sin ( θ ) ( n × p ) + p ∥ = cos ( θ ) ( p − p ∥ ) + p ∥ + sin ( θ ) ( n × p ) = cos ( θ ) p + ( 1 − cos ( θ ) ) ( n ⋅ p ) n + sin ( θ ) ( n × p ) \begin{gathered}\mathbf{p}^{\prime}=\mathbf{p}_{\perp}^{\prime}+\mathbf{p}_{\|}^{\prime}=\cos (\theta) \mathbf{p}_{\perp}+\sin (\theta)(\mathbf{n} \times \mathbf{p})+\mathbf{p}_{\|} \\ =\cos (\theta)\left(\mathbf{p}-\mathbf{p}_{\|}\right)+\mathbf{p}_{\|}+\sin (\theta)(\mathbf{n} \times \mathbf{p}) \\ =\cos (\theta) \mathbf{p}+(1-\cos (\theta))(\mathbf{n} \cdot \mathbf{p}) \mathbf{n}+\sin (\theta)(\mathbf{n} \times \mathbf{p})\end{gathered} p′=p⊥′+p∥′=cos(θ)p⊥+sin(θ)(n×p)+p∥=cos(θ)(p−p∥)+p∥+sin(θ)(n×p)=cos(θ)p+(1−cos(θ))(n⋅p)n+sin(θ)(n×p)
即:
p ′ = cos θ ( p − ( n ⋅ p ) n ) + ( n ⋅ p ) n + sin θ ( n × p ) \mathbf{p}^{\prime}=\cos\theta (\mathbf{p}-(\mathbf{n} \cdot \mathbf{p}) \mathbf{n})+(\mathbf{n} \cdot \mathbf{p}) \mathbf{n}+\sin\theta(\mathbf{n} \times \mathbf{p}) p′=cosθ(p−(n⋅p)n)+(n⋅p)n+sinθ(n×p)
写成这种形式,因为计算机里面算三角函数的开销大于坐标运算。
内坐标转笛卡尔坐标;二面角复原
欲求 D C ⃗ \vec{DC} DC, 将其分解为 C B ⃗ \vec{CB} CB 上的分量,和 垂直于 C B ⃗ \vec{CB} CB 的分量。
(align with , orthogonal to C B ⃗ \vec{CB} CB)
已知距离和bond angle,align with 的分量很好求
D C ⃗ a l i g n = d cos α C B ⃗ ∣ C B ⃗ ∣ \vec{DC}_{align} = d\cos \alpha\frac{\vec{CB}}{|\vec{CB}|} DCalign=dcosα∣CB∣CB。
复杂一点的是垂直分量。
先计算 B A ⃗ \vec{BA} BA 在 C B ⃗ \vec{CB} CB上的分量。
t ⃗ = B A ⃗ ⋅ C B ⃗ ∣ C B ⃗ ∣ C B ⃗ ∣ C B ⃗ ∣ = ( B A ⃗ ⋅ u ⃗ C B ) u ⃗ C B \vec{t}= \frac{\vec{BA}\cdot \vec{CB}}{|\vec{CB}|} \frac{\vec{CB}}{|\vec{CB}|} = (\vec{BA}\cdot \vec{u}_{CB}) \vec{u}_{CB} t=∣CB∣BA⋅CB∣CB∣CB=(BA⋅uCB)uCB , u ⃗ \vec{u} u 表示单位向量。
然后得到 B A ⃗ \vec{BA} BA垂直于 C B ⃗ \vec{CB} CB的分量
v ⃗ = B A ⃗ − t ⃗ \vec{v}=\vec{BA} - \vec{t} v=BA−t。
从后文可以知道,这一步如果把 B A ⃗ \vec{BA} BA 归一化为单位向量也无妨,因为我们在乎的只有方向。
按上文所言,以 C B ⃗ \vec{CB} CB为视角,从逆向往正向看,建立平面坐标系。
以 v ⃗ \vec{v} v为该平面上的 x ′ x' x′ 轴,
约定该平面上 y ′ y' y′ 轴正向是 v ⃗ × C B ⃗ \vec{v}\times\vec{CB} v×CB (右手定则)。
D C ⃗ \vec{DC} DC在该平面上的分量即为 D C ⃗ \vec{DC} DC垂直于 C B ⃗ \vec{CB} CB的分量。
根据上文的旋转角(广义二面角)定义, D C ⃗ \vec{DC} DC在该平面上的分量,
即为 v ⃗ \vec{v} v逆时针旋转{dihedral}度得到的向量。
即,问题变成了求 v ⃗ \vec{v} v 绕 C B ⃗ \vec{CB} CB 逆时针旋转 {dihedral} 度得到的向量。
应用上文所言的旋转公式
其中 旋转轴为 n ⃗ = C B ⃗ \vec{n}=\vec{CB} n=CB,
w ⃗ = cos θ ( v ⃗ − ( n ⃗ ⋅ v ⃗ ) n ⃗ ) + ( n ⃗ ⋅ v ⃗ ) n ⃗ + sin θ ( n ⃗ × v ⃗ ) \vec{w} = \cos \theta (\vec{v}-(\vec{n} \cdot \vec{v})\vec{n}) + (\vec{n}\cdot \vec{v})\vec{n} +\sin\theta (\vec{n}\times \vec{v}) w=cosθ(v−(n⋅v)n)+(n⋅v)n+sinθ(n×v)。
由于按照定义 v ⃗ \vec{v} v是垂直于 C B ⃗ \vec{CB} CB的分量,故两者内积为0。
上式进一步化简为
w ⃗ = cos θ v ⃗ + sin θ ( n ⃗ × v ⃗ ) \vec{w}=\cos\theta \vec{v} +\sin\theta (\vec{n}\times \vec{v}) w=cosθv+sinθ(n×v)
旋转后的方向得到了,再考虑长度。
由键长知
D C ⃗ o r t h o = ∣ d sin α ∣ w ⃗ ∣ w ⃗ ∣ \vec{DC}_{ortho}=|d\sin\alpha| \frac{\vec{w} }{|\vec{w} |} DCortho=∣dsinα∣∣w∣w, 由于约定了键角[0,pi), sin α > 0 \sin \alpha >0 sinα>0。
D C ⃗ o r t h o = d sin α w ⃗ ∣ w ⃗ ∣ \vec{DC}_{ortho}=d\sin\alpha \frac{\vec{w} }{|\vec{w} |} DCortho=dsinα∣w∣w。
最后
D C ⃗ = D C ⃗ a l i g n + D C ⃗ o r t h o = d cos α u ⃗ C B + d sin α u ⃗ w \vec{DC}=\vec{DC}_{align} + \vec{DC}_{ortho} = d\cos \alpha \vec{u}_{CB} + d\sin\alpha \vec{u}_{w} DC=DCalign+DCortho=dcosαuCB+dsinαuw;
u ⃗ \vec{u} u 表示单位向量。
于是D的坐标 = D C ⃗ + C \vec{DC}+C DC+C。
前三个点处理
第一个点,按习惯固定(0,0,0)
第二个点,我看大部分库都默认放到z-axis上。于是(0, 0, dst)。
第三个点,按照距离和键角可以获得一个圆锥,约定第三个点放在zoy平面的y轴正半面上。
或者可以用兼容第4个点的方式说,
在y轴正向有一个假想点y, 于是(C,B,A,y) 构成的二面角为0。
注意!
本文默认坐标是(x,y,z)顺序。
测试样例
下图为例,左边是输入坐标。
右边是我们希望还原得到的坐标。
A在原点,B在z轴,c在zoy平面。
这等价于对原输入做一次平移和一次90度旋转。

# test
#输入
input_coord=torch.tensor([[1,0,0],[0,0,0],[0,2,0],[0,0,2]])
# 内坐标
inner_coord = torch.tensor([1.0000, 2.0000, 2.8284, 1.5708, 0.7854, -1.5708]
)
# 还原坐标
output_coord=torch.tensor([[0.0000e+00, 0.0000e+00, 0.0000e+00],[0.0000e+00, 0.0000e+00, 1.0000e+00],[0.0000e+00, 2.0000e+00, 1.0000e+00],[2.0000e+00, 1.1921e-07, 1.0000e+00]])
其他坐标系的兼容
主流的一些3D库,化学库,有些用的(z,x,y) 或者 (z, y, x)坐标顺序。
这个也简单。
我们返回的坐标交换一下顺序就能得到其他坐标系了。
output_coord[:, [1,2,0]] -> (z,x,y) 坐标。
speed test
cart2internal + internal2cart。
1w个样本约30.6s。
100w 样本约 1h。
相关文章:

内坐标转换计算
前言 化学这边的库太多了。 cs这边的库太少了。 去看化学的库太累了。 写一个简单的实现思路,让cs的人能看懂。 向量夹角的范围 [0, pi) 这是合理的。 因为两个向量只能构成一个平面系统,平面系统内的夹角不能超过pi。 二面角的范围 涉及二面角&…...

vue中 components自动注册,不需要一个个引入注册方法
1.在compontents文件夹新建js文件 componentRegister 不能引用文件夹里的组件** import Vue from "vue"; function capitalizeFirstLetter(string) { return string.charAt(0).toUpperCase() string.slice(1); } const requireComponent require.context( ".…...

web自动化测试从入门到持续集成
在很多刚学习自动化的可能会认为我只需要会运用selenium,我只需要在一个编辑器中实用selenium java编写了一些脚本那么就会自动化了,是真的吗?答案肯定是假的。自动化肯定是需要做到真的完全自动化,那如何实现呢?接着往…...
python小工具之弱密码检测工具
一、引用的python模块 Crypto: Python中一个强大的加密模块,提供了许多常见的加密算法和工具。它建立在pyc.ypodome或pyc.ypto等底层加密库之上,为Python程序员提供了简单易用的API,使其可以轻松地实现各种加密功能。 commands…...
链接器--动态链接器--延迟绑定与动态链接器是什么?学习笔记二
内容在下面链接(通过新建标签页打开): 链接器--动态链接器--延迟绑定与动态链接器是什么?学习笔记二一个例子来看延迟加载https://mp.weixin.qq.com/s?__bizMzkyNzYzMjMzNA&mid2247483713&idx1&snee90a5a7d59872287…...

JMeter CSV 参数文件的使用方法
.在 JMeter 测试中,参数化是非常重要的,参数化允许我们模拟真实世界中的各种情况。本文我们将探讨如何在 JMeter 中使用 CSV 参数文件。 创建 CSV 文件 首先,我们需要创建一个逗号分隔的值(CSV)文件,其中…...
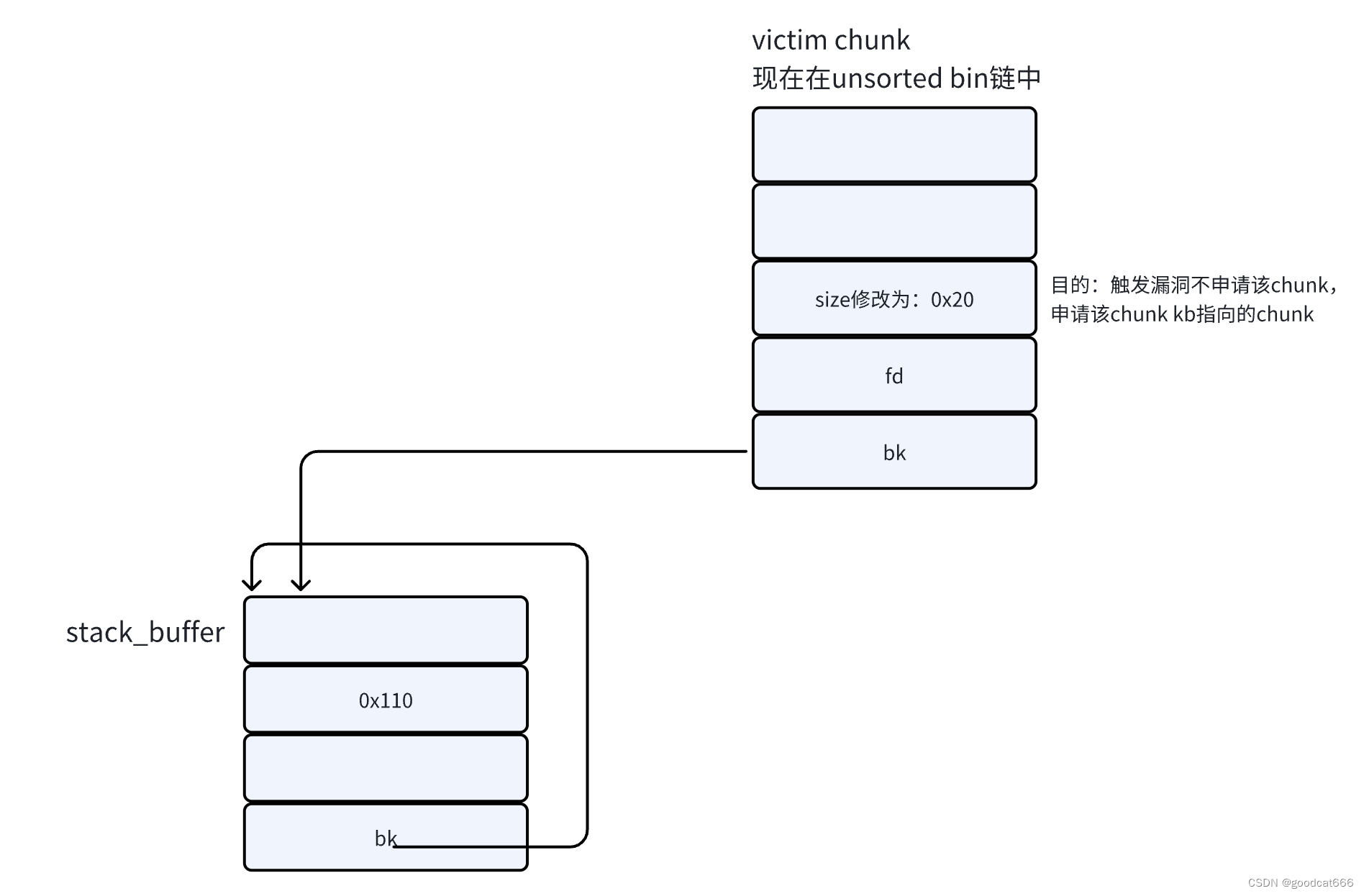
how2heap-2.23-06-unsorted_bin_into_stack
#include <stdio.h> #include <stdlib.h> #include <stdint.h> #include <string.h>// 从 unsorted bin 的 bk 去找合适的 void jackpot(){ fprintf(stderr, "Nice jump d00d\n"); exit(0); }int main() {intptr_t stack_buffer[4] {0};fpr…...

(学习打卡2)重学Java设计模式之六大设计原则
前言:听说有本很牛的关于Java设计模式的书——重学Java设计模式,然后买了(*^▽^*) 开始跟着小傅哥学Java设计模式吧,本文主要记录笔者的学习笔记和心得。 打卡!打卡! 六大设计原则 (引读:这里…...
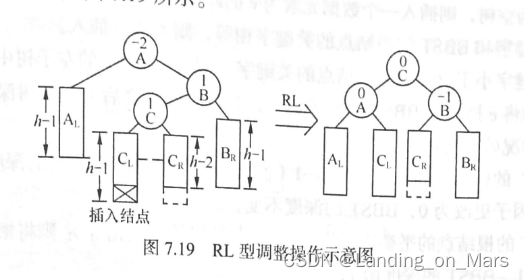
数据结构:第7章:查找(复习)
目录 顺序查找: 折半查找: 二叉排序树: 4. (程序题) 平衡二叉树: 顺序查找: ASL 折半查找: 这里 j 表示 二叉查找树的第 j 层 二叉排序树: 二叉排序树(Binary Search Tree&…...

编程语言的未来?
编程语言的未来? 随着科技的飞速发展,编程语言在计算机领域中扮演着至关重要的角色。它们是软件开发的核心,为程序员提供了与机器沟通的桥梁。那么,在技术不断进步的未来,编程语言的走向又将如何呢? 在技…...

SpringBoot的测试
🙈作者简介:练习时长两年半的Java up主 🙉个人主页:程序员老茶 🙊 ps:点赞👍是免费的,却可以让写博客的作者开心好久好久😎 📚系列专栏:Java全栈,…...

C++睡眠函数:Windows平台下的Sleep函数和Linux平台的usleep函数
C/C睡眠函数:Windows平台下的Sleep函数和Linux平台的usleep函数 WinAPI Sleep Sleep函数属于Windows API,使用它需要先包含synchapi.h。 void Sleep(DWORD dwMilliseconds);函数仅有一个参数(睡眠时长),单位是毫秒。…...

详解白帽子以及红队、蓝队和紫队
企业继续数字化,其关键基础设施和运营扩大了攻击面,暴露于各种威胁途径的面前。为了解决这个问题,企业领导者认识到拥有内部专家的重要性。考虑到网络威胁领域不断发展的态势,企业领导者可以利用道德黑客以及红队、蓝队和紫队的工…...

1、docker常用技巧:docker数据位置更改
目录 🍅点击这里查看所有博文 随着自己工作的进行,接触到的技术栈也越来越多。给我一个很直观的感受就是,某一项技术/经验在刚开始接触的时候都记得很清楚。往往过了几个月都会忘记的差不多了,只有经常会用到的东西才有可能真正记…...

Qt之设置QLabel的背景色和前景色
方法有两种,一种是使用调色板,一种是使用样式表。 方法一:调色板 QPalette palette ; // 设置黑底绿字 palette .setColor(QPalette::Background, Qt::black); palette .setColor(QPalette::WindowText, Qt::green); // 这句不能少,否则没效果 ui->label->setAutoF…...
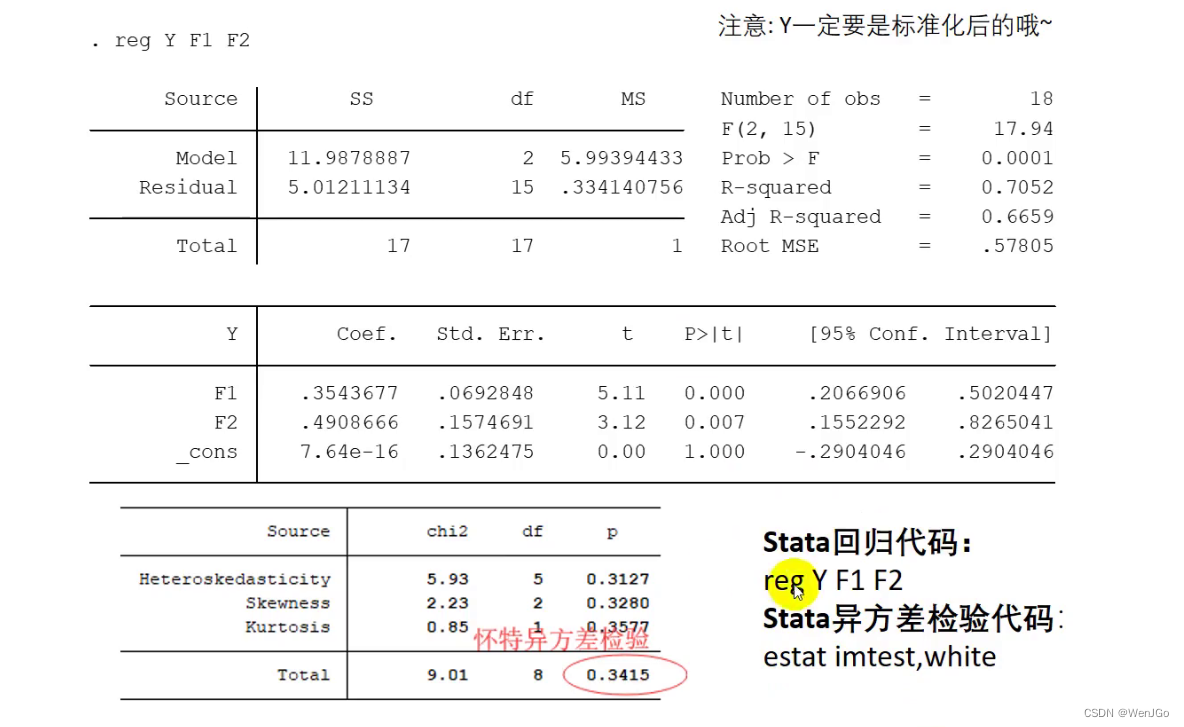
数模学习day06-主成分分析
主成分分析(Principal Component Analysis,PCA)主成分分析是一种降维算法,它能将多个指标转换为少数几个主成分,这些主成分是原始变量的线性组合,且彼此之间互不相关,其能反映出原始数据的大部分信息。一般来说当研究的问题涉及到…...

Windows PowerShell的安全目标——安全警报
Windows PowerShell的安全目标——安全警报 1. 保证Shell安全 自从2006年年底PowerShell发布以来,微软在安全和脚本方面并没有取得很好的名声。毕竟那个时候,**VBScript和Windows Script Host(WSH)**是两个最流行的病毒和恶意软件的载体,…...
k8s笔记1- 初步认识k8s
k8s简介: kubernetes,俗称k8是,用于自动部署,扩缩和管理容器化应用程序的开源系统,它将组成应用程序的容器,组合成逻辑单元,便于管理和服务发现。 k8s的作用 自动化上线和回滚、存储编排…...
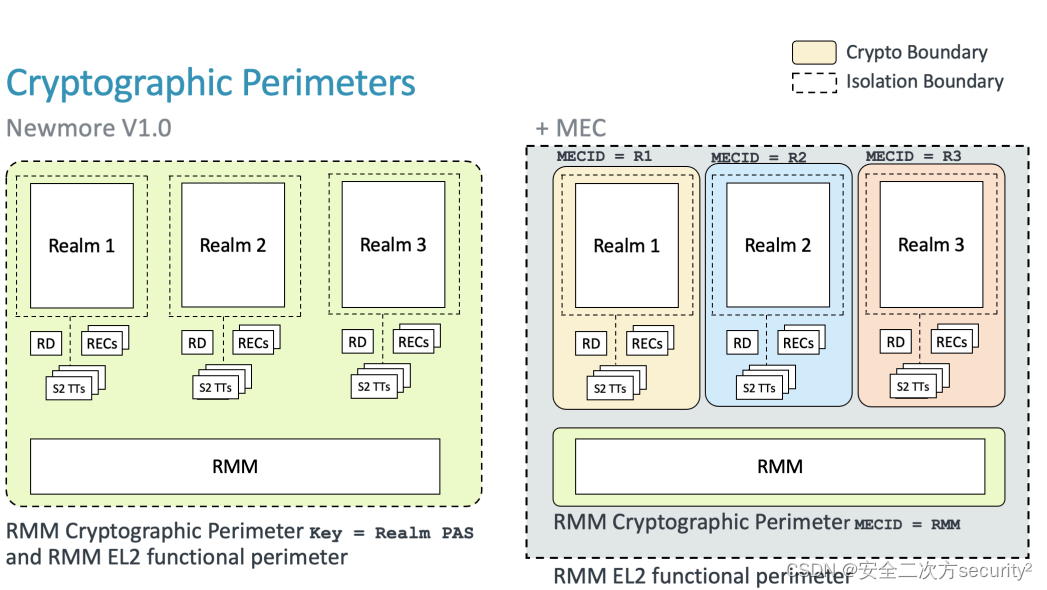
ARM CCA机密计算软件架构之内存加密上下文(MEC)
内存加密上下文(MEC) 内存加密上下文是与内存区域相关联的加密配置,由MMU分配。 MEC是Arm Realm Management Extension(RME)的扩展。RME系统架构要求对Realm、Secure和Root PAS进行加密。用于每个PAS的加密密钥、调整或加密上下文在该PAS内是全局的。例如,对于Realm PA…...

python基于flask实现一个文本问答系统
from flask import Flask, render_template, requestapp Flask(__name__)# 一个简单的问题-答案映射,实际中可以使用更复杂的存储结构(数据库等) qa_pairs {"什么是人工智能?": "人工智能是模拟人类智能的一种机…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...
