数据结构学习笔记——查找算法中的树形查找(B树、B+树)
目录
- 前言
- 一、B树
- (一)B树的概念
- (二)B树的性质
- (三)B树的高度
- (四)B树的查找
- (五)B树的插入
- (六)B树的删除
- 二、B+树
- (一)B+树的概念
- (二)B+树的性质
- (三)B+树的查找
前言
B树和B+树属于树形查找算法中的一种,主要用于数据库系统、文件系统和磁盘存取等方面,都是用于存储和索引大量的数据,以提高检索效率。例如,在磁盘存储中,通过将数据分散到多个磁盘块中,并使用树形结构来组织这些磁盘块,从而提高了查找速度和查找效率。若设B树中所有结点的孩子结点个数的最大值为m,则该B树是一棵m阶B树,另外B+树则是B树的变形。
一、B树
(一)B树的概念
二叉排序树也称为查找树(注意:与二分查找的判定树不同),其中各结点值的大小关系是:左子树<根结点<右子树,且左、右子树也是一棵二叉排序树满足其条件。
前面给过二叉查找树的定义,简单的来说,B树是二叉查找树的推广,即一棵m阶B树可看作一棵m叉查找树,但两者有些方面不同,如下:
1、结点与关键字不同:二叉查找树遵循二叉树的原则,每个结点最多只有两个孩子结点,且每个结点只包含一个关键字;而B树的每个结点最多有m个结点,即最多含有m-1个关键字。
2、平衡性:二叉查找树不一定是一棵平衡二叉树,查找过程中查找效率可能随着查找树的结构变化;而B树是一棵多路平衡查找树,通过限制结点的子树和关键字数量,使B树的高度保持相对稳定,从而提高查找效率。B树也正是在保持平衡的前提下能够更高效地处理大量数据,从而非常适合应用在需要高效存储和访问大量数据的场景中。
(二)B树的性质
B树中与二叉查找树相同的性质,二叉查找树各结点值的大小关系是:左子树<根结点<右子树,而B树中关键字的值的大小关系是:子树1<关键字1<子树2<关键字2<子树3…,一棵m阶B树中,除了根结点外所有结点中关键字个数为:⌈m/2⌉-1 ≤ n ≤ m-1。例如,一棵5阶B树中,除了根结点外所有结点中关键字的个数为2 ≤ n ≤ 4,即关键字个数最少为2,最多为4。
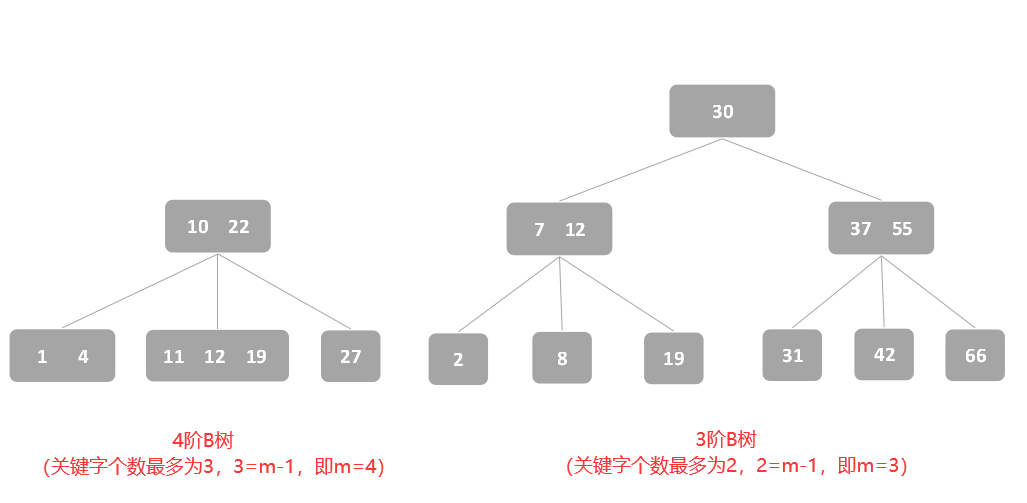
1、m阶B树中,根结点至多有m棵子树,若B树的根结点不是终端结点,则该B树至少有两棵子树。
2、B树中结点内关键字均以升序或降序排列。
3、B树是一棵多路平衡查找树,所有结点的平衡因子均为0。
4、m阶B树中,若根结点没有关键字,则B树无子树,B树为空;若有关键字,由于子树个数等于关键字个数加1,所以子树一定大于或等于两棵。
5、m阶B树中,根结点最少含1个关键字,而除根结点外,每个非叶子结点至少有⌈m/2⌉棵子树,且至少有⌈m/2⌉-1个关键字;由于最少情况下,根结点至少有一个关键字,所以B树中所有结点包括的关键字个数至少为(n-1)(⌈m/2⌉-1)+1个。
6、结点的孩子结点的个数等于该结点关键字的个数加1,即具有n个关键字的m阶B树,应有n+1个叶结点。另外,B树中所有的叶子结点均在一层上,且不带任何信息,这一点与二分查找判定树中查找失败的结点类似,实际上这些叶子结点不存在,代表查找失败的情况,如下:
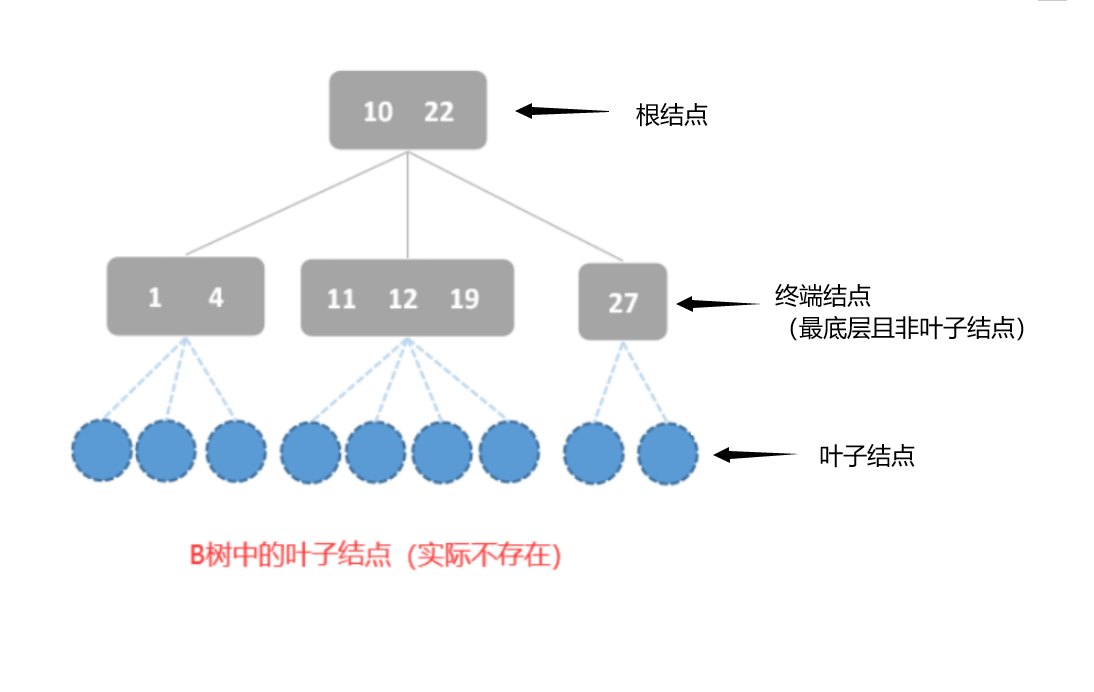
(三)B树的高度
在求B树的高度时,不计入叶子结点,若设m阶B树中包括n(n≥1)个关键字,其高度为h,可得到B树的最小高度和最大高度范围区间:logm(n+1) ≤ h ≤ log⌈m/2⌉[(n+1)/2]+1。
⌈ ⌉表示向上取整,取比自己大的最小整数,⌊ ⌋表示向下取整,取比自己小的最大整数。
(四)B树的查找
B树的查找类似二叉查找,首先在B树中查找结点,然后在结点所包含的关键字K1,…,Kn中查找给定的关键字,可通过顺序查找或二分查找进行查找,若找到等于给定值的关键字,则查找成功;否则,继续查找,直至找到或指针为空时,此时查找失败,即查找到B树的叶子结点时失败。
(五)B树的插入
B树的插入操作不仅需要找到要插入的位置(定位),而且需判断插入后是否会导致不满足B树的定义,由于B树中查找成功结点的关键字个数在 ⌈m/2⌉-1 ≤ n ≤ m-1间,如下:
1、第一种情况:若插入后结点的关键字个数小于m,则直接插入。
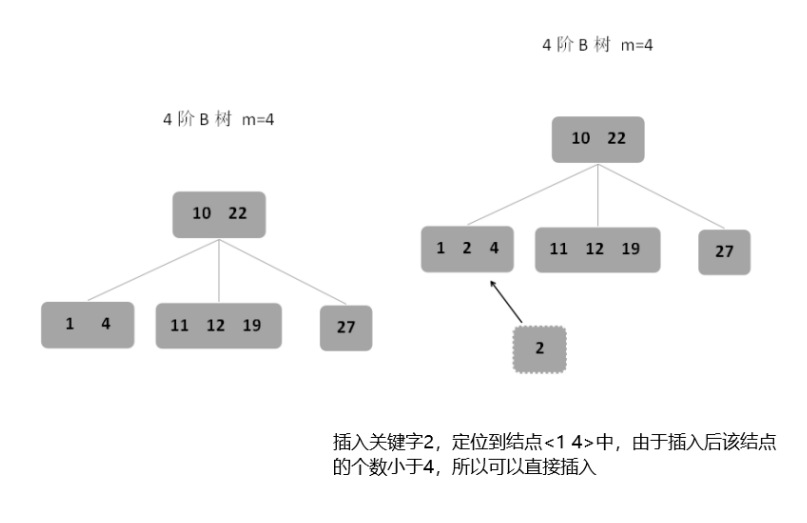
2、第二种情况:若插入后结点的关键字个数大于m-1,则需要进行调整,从关键字中间位置⌈m/2⌉处将关键字分为两部分,左半部分放在原结点中,右半部分放在新的相邻右边结点中,中间关键字元素⌈m/2⌉上移到原结点的父结点中,另外,若父结点的空间也不够,则继续按照以上方式进行调整。
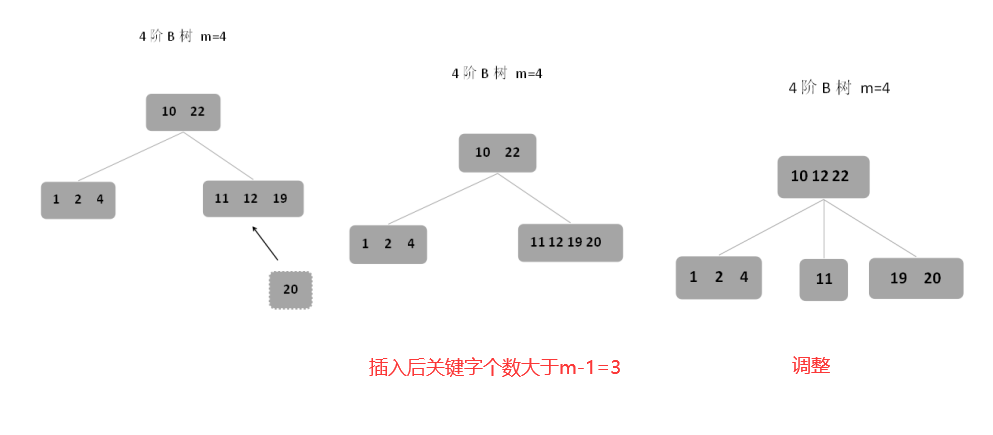
(六)B树的删除
B树的删除分两种情况,如下:
1、第一种情况:
若要删除的关键字在终端结点中时:
(1)若要删除的关键字所在结点的关键字个数大于或等于⌈m/2⌉时,即关键字删除后结点仍满足相应的关键字个数,则可直接删去。
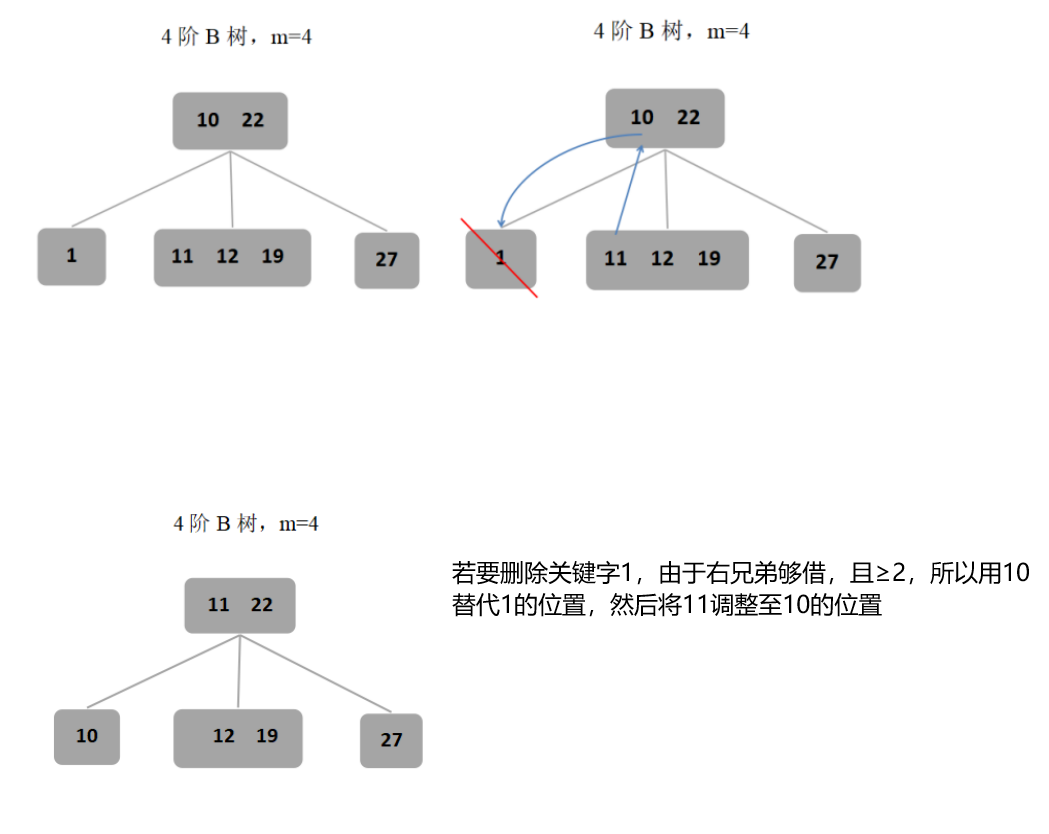
(2)若要删除的关键字当前所在结点的关键字个数等于⌈m/2⌉-1时,且左/右兄弟很充裕时,即其关键字个数大于或等于⌈m/2⌉时,需要进行调整(向兄弟借),用当前结点的前驱/后继、前驱的前驱/后继的后继代替,从而满足B树的定义。
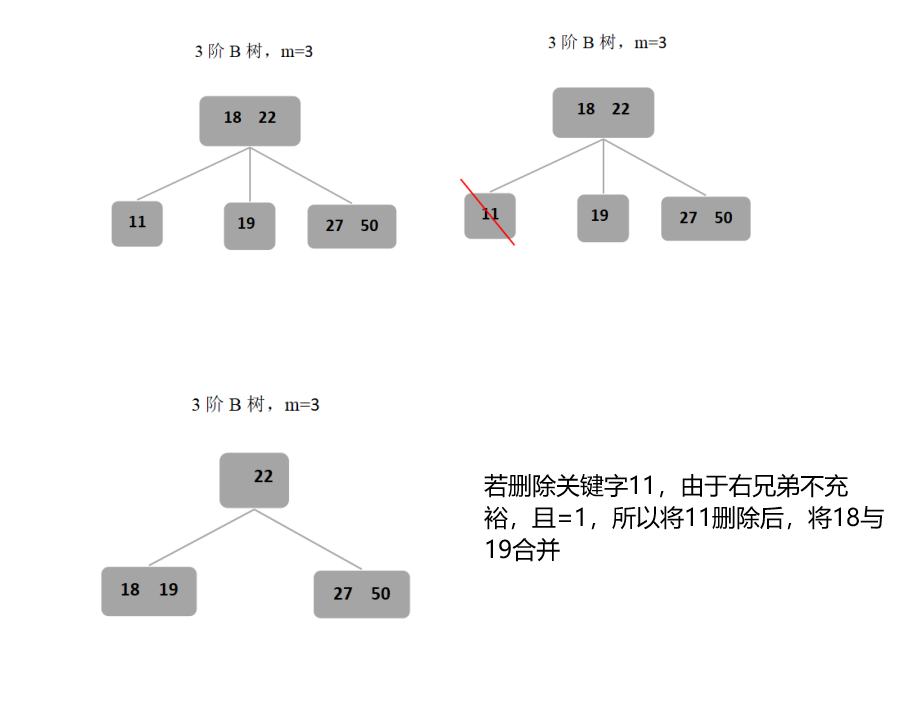
(3)若要删除的关键字当前所在结点的关键字个数等于⌈m/2⌉-1时,且左/右兄弟不是很充裕时,即其关键字个数只等于⌈m/2⌉-1时,则将关键字删除后需要进行合并,即与当前结点的兄弟结点以及双亲结点中的关键字合并。
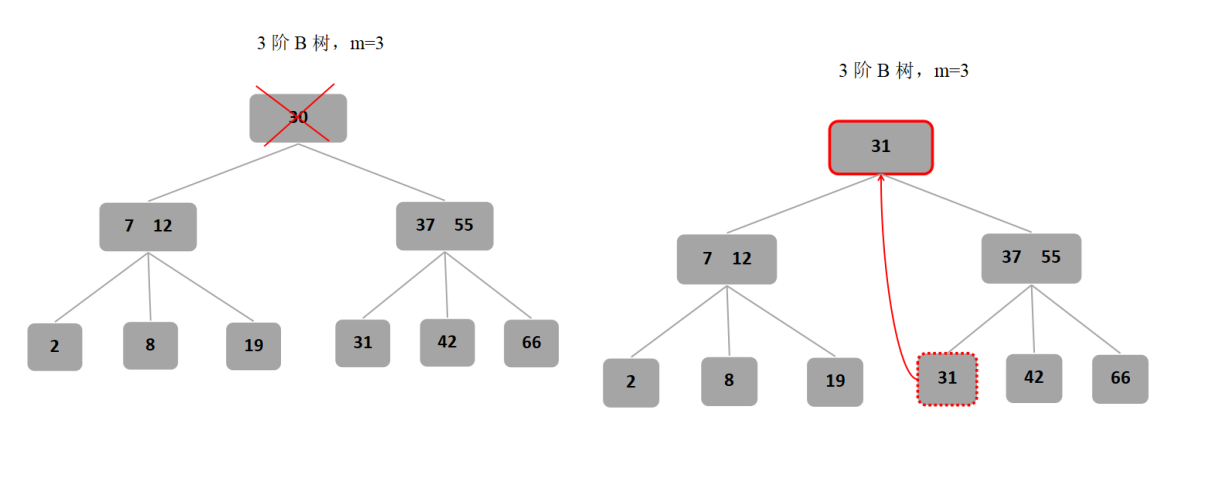
2、第二种情况:
若要删除的关键字不在终端结点中时,用该关键字的直接前驱或直接后继代替,转换成第一种情况,再进行删除。

二、B+树
(一)B+树的概念
B+树可以由分块查找推广,所以也称为多级分块查找,即m阶B+树,它是B树的变形,与B树相同,B树和B+树都是平衡的多叉树,都用在文件索引结构和数据库索引中,但B+树更加适用。B树的结点包含关键字对应记录的存储地址,且B树中的叶子结点不带信息,而B+树的叶子结点带信息,而其中其他的非叶子结点只是作索引作用。
(二)B+树的性质
B+树中,n个关键字对应n棵子树,即每个关键字对应一棵子树,且子树的个数与结点的关键字个数相等,每个分支结点至少有 ⌈m/2⌉棵子树。
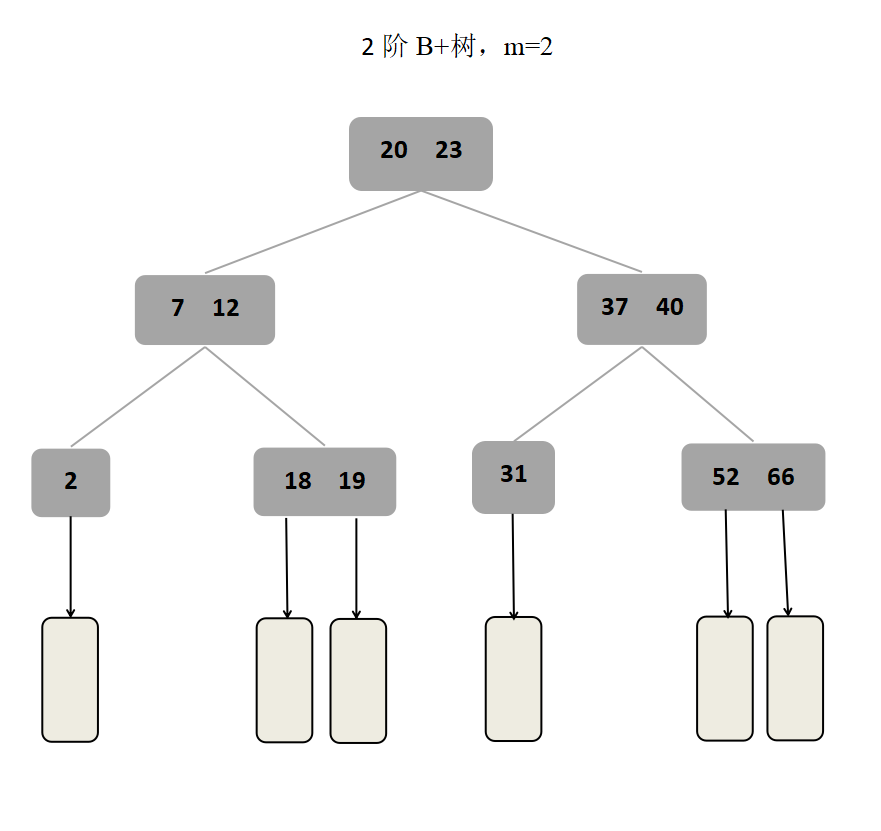
B树与B+树中结点的关键字个数对比如下表:
| 名称 | B树 | B+树 |
|---|---|---|
| 根结点关键字个数 | 1 ≤ n ≤ m-1 | 2 ≤ n ≤ m |
| 非根结点关键字个数 | ⌈m/2⌉-1 ≤ n ≤ m-1 | ⌈m/2⌉ ≤ n ≤ m |
(三)B+树的查找
B树支持随机查找,而B+树支持顺序查找和随机查找。
B树不支持顺序查找的原因是查找时可能查找到树中的任何一层,所以其查找速度和稳定性没有B+树高。
相关文章:

数据结构学习笔记——查找算法中的树形查找(B树、B+树)
目录 前言一、B树(一)B树的概念(二)B树的性质(三)B树的高度(四)B树的查找(五)B树的插入(六)B树的删除 二、B树(一…...
python包chromadb安装失败总结
1,背景: 最近在学习langchain的课程,里面创建自己的知识库的Retrieval模块中,需要用到向量数据库。 所以按照官方的教程(vectorstores),准备使用chroma的向量数据库。图片来源 2,问…...

机器学习(四) -- 模型评估(2)
系列文章目录 机器学习(一) -- 概述 机器学习(二) -- 数据预处理(1-3) 机器学习(三) -- 特征工程(1-2) 机器学习(四) -- 模型评估…...

泊松分布与二项分布的可加性
泊松分布与二项分布的可加性 泊松分布的可加性 例 : 设 X , Y X,Y X,Y 相互独立 , X ∼ P ( λ 1 ) X\sim P(\lambda_1) X∼P(λ1) , Y ∼ P ( λ 2 ) Y\sim P(\lambda_2) Y∼P(λ2) , 求证 Z X Y ZXY ZXY 服从参数为 λ 1 λ 2 \lambda_1 \lambda_2 λ1λ2 …...

【PostgreSQL】约束-排他约束
【PostgreSQL】约束链接 检查 唯一 主键 外键 排他 排他约束 排他约束是一种数据库约束,用于确保某一列或多个列中的值在每一条记录中都是唯一的。这意味着任何两条记录都不能具有相同的值。 排他约束可以在数据库中创建唯一索引或唯一约束来实现。当尝试插入或更…...

Java重修第一天—学习数组
1. 认识数组 建议1.5倍速学习,并且关闭弹幕。 数组的定义:数组是一个容器,用来存储一批同种类型的数据。 下述图:是生成数字数组和字符串数组。 为什么有了变量还需要定义数组呢?为了解决在某些场景下,变…...
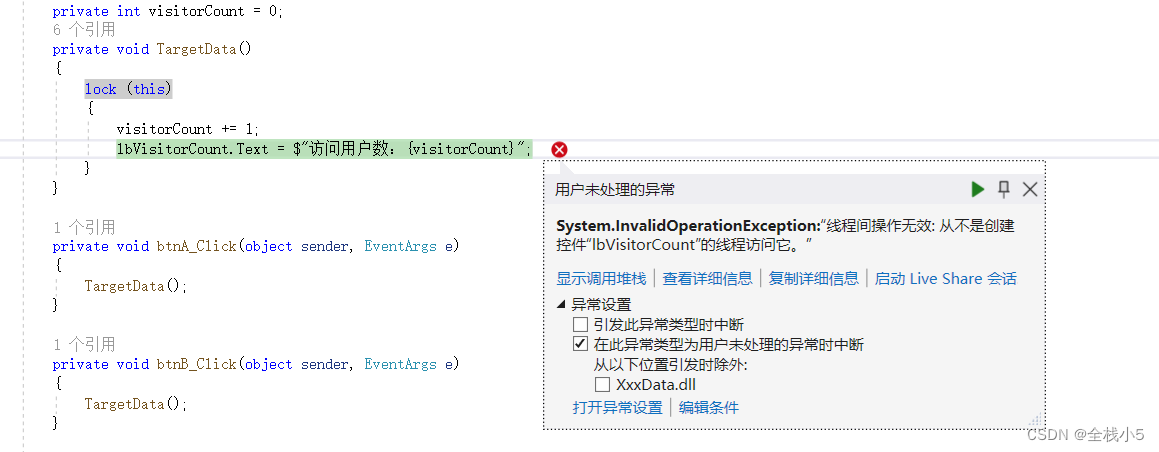
【C#】知识点实践序列之Lock的锁定代码块
大家好,我是全栈小5,欢迎来到《小5讲堂之知识点实践序列》文章。 2024年第1篇文章,此篇文章是C#知识点实践序列之Lock知识点,博主能力有限,理解水平有限,若有不对之处望指正! 本篇验证Lock锁定代…...
)
StringBad ditto (motto)
第12章 类和动态内存分配 StringBad ditto (motto): // calls StringBad (comst StringBad &) StringBad metoo - motto: // calls StringBad (const StringBad &) StringBad also StringBad (motto): // calls StringBad (const StringBad &) StringBad * pStri…...

Redis缓存击穿、缓存雪崩、缓存穿透
缓存击穿(某个热点key缓存失效) 概念 缓存中没有但数据库中有的数据,假如是热点数据,那key在缓存过期的一刻,同时有大量的请求,这些请求都会击穿到DB,造成瞬时DB请求量大、压力增大和缓存雪崩的…...

【PCB专题】Allegro封装更新焊盘
在PCB封装的绘制中,有时会出现需要更新焊盘的情况。比如在制作封装的过程中发现焊盘做的不对而使用PAD_Designer重新更新了焊盘。 那在PCB中如何更新已经修改过的焊盘呢? 打开封装,选择Tools->Padstack->Refresh... 选择Refresh all …...
ES6之Reflect详解
✨ 专栏介绍 在现代Web开发中,JavaScript已经成为了不可或缺的一部分。它不仅可以为网页增加交互性和动态性,还可以在后端开发中使用Node.js构建高效的服务器端应用程序。作为一种灵活且易学的脚本语言,JavaScript具有广泛的应用场景&#x…...

文件监控-IT安全管理软件
文件监控和IT安全管理软件是用于保护企业数据和网络安全的工具。这些工具可以帮助企业监控文件的变化,防止未经授权的访问和修改,并确保数据的安全性和完整性。 一、具有哪些功能 文件监控软件可以实时监控文件系统的活动,包括文件的创建、修…...
达梦数据库安装超详细教程(小白篇)
文章目录 达梦数据库一、达梦数据库简介二、达梦数据库下载三、达梦数据库安装1. 解压2. 安装 四、初始化数据库五、DM管理工具 达梦数据库 一、达梦数据库简介 达梦数据库管理系统是达梦公司推出的具有完全自主知识产权的高性能数据库管理系统,简称DM。 达梦数…...
算法篇)
复试 || 就业day09(2024.01.04)算法篇
文章目录 前言验证外星语词典在长度 2N 的数组中找出重复 N 次的元素找到小镇的法官查找共用字符数组的相对排序分发饼干分发糖果区间选点(AcWing)最大不相交区间数量(AcWing)无重叠区间关于重写小于号 前言 💫你好,我是辰chen,本文旨在准备考…...
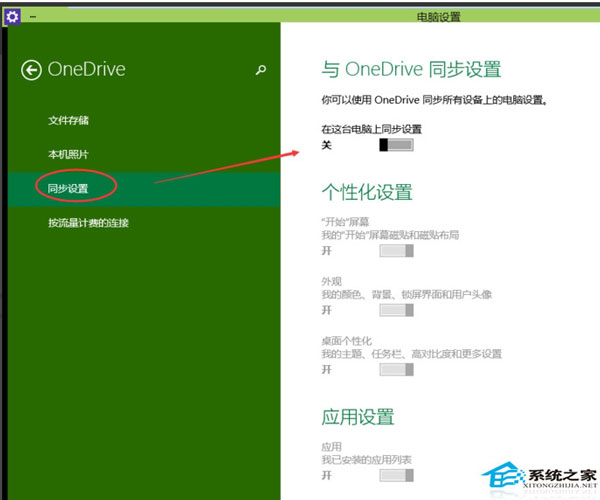
Win10电脑关闭OneDrive自动同步的方法
在Win10电脑操作过程中,用户想要关闭OneDrive的自动同步功能,但不知道具体要怎么操作?首先用户需要打开OneDrive,然后点击关闭默认情况下将文档保存到OneDrive选项保存,最后关闭在这台电脑上同步设置保存就好了。接下来…...

linux(centos)相关
文件架构: bin--binary--二进制命令,可直接执行 sbin systembin系统二进制命令,超级管理员 lib 库目录 类似dll文件 lib64 64位系统相关的库文件 usr 用户文件 boot 引导分区的文件,链接,系统启动等 dev device设备目录…...

外贸网站显示不安全警告怎么办?消除网站不安全警告超全指南
外贸网站显示不安全警告怎么办?当用户访问你的网站,而您的网站没有部署SSL证书实现HTTPS加密时,网站就会显示不安全警告,这种警告,不仅有可能阻止用户继续浏览网站,影响网站声誉,还有可能影响网…...

Java:HeapMemory和DirectMemory配置与使用介绍
目录 一、Heap内存 1、查看Heap内存配置的最大值 2、配置Heap内存最大值的方式 3、配置Heap内存最小值的方式 4、查看已使用Heap内存的方式 5、查看未使用Heap内存的方式 二、Direct内存 1、查看Direct内存配置的最大值 2、配置Direct内存最大值的方式 3、获取Direct…...

记 -bash: docker-compose: command not found 的问题解决
docker-compose: command not found 错误表明系统无法找到 docker-compose 命令。这可能是因为 docker-compose 并未正确安装,或者其可执行文件的路径未包含在系统的 PATH 变量中。 以下是我遇到时解决方法: 确保 Docker 和 Docker Compose 已安装&…...
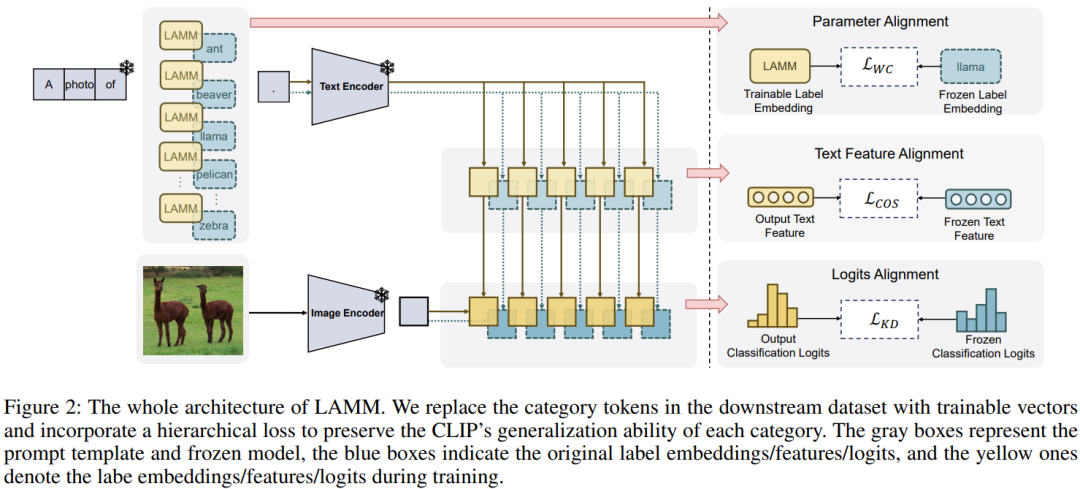
分享10篇优秀论文,涉及图神经网络、大模型优化、表格分析
引言 第38届AAAI人工智能年度会议将于2024年2月在加拿大温哥华举行。今天给大家分享十篇AAAI2024论文,主要涉及图神经网络,大模型幻觉、中文书法文字生成、表格数据分析、KGs错误检测、多模态Prompt、思维图生成等。 论文获取方式,回复&am…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
