【强化学习】强化学习数学基础:蒙特卡洛方法
强化学习数学方法:蒙特卡洛方法
- 举个例子
- 举个例子1:投掷硬币
- The simplest MC-based RL algorithm
- 举个例子2:Episode length
- Use data more efficiently
- MC without exploring starts
- 总结
- 内容来源
将value iteration和policy iteration方法称为model-based reinforcement learning方法,这里的Monte Carlo方法称为model-free的方法。
举个例子
如何在没有模型的情况下估计某些事情?最简单的想法就是Monte Carlo estimation。
举个例子1:投掷硬币

目标是计算E[X]\mathbb{E}[X]E[X]。有两种方法:
Method 1: Model-based

这个方法虽然简单,但是问题是它不太可能知道precise distribution。
Method 2: Model-free
该方法的思想是将硬币投掷很多次,然后计算结果的平均数。

问题:Monte Carlo估计是精确的吗?
- 当N是非常小的时候,估计是不精确的
- 随着N的增大,估计变得越来越精确
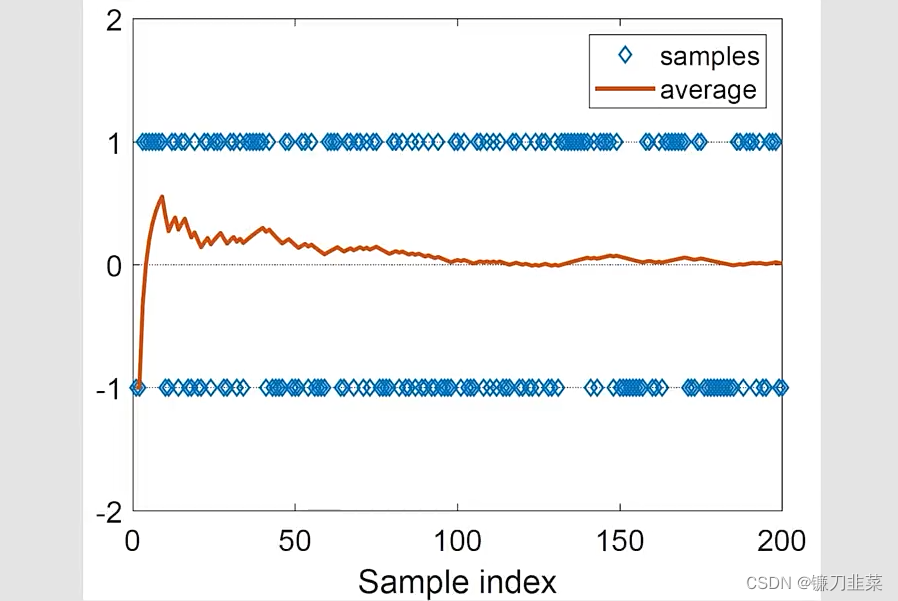
大数定理(Law of Large Numbers):

注意:样本必须是独立同分布的(iid, independent and identically distributed)
小结一下:
- Monte Carlo estimation refers to a broad class of techniques that rely on repeated random sampling to solve appriximation problems.
- Why we care about Monte Carlo estimation? Because it does not require the model!
- Why we care about mean estimation? Because state value and action value are defined as expectations of random variables!
The simplest MC-based RL algorithm
Algorithm: MC Basic
理解该算法的关键是理解how to convert the policy iteration algorithm to be model-free
Convert policy iteration to be model-free
首先,策略迭代算法在每次迭代中分为两步:
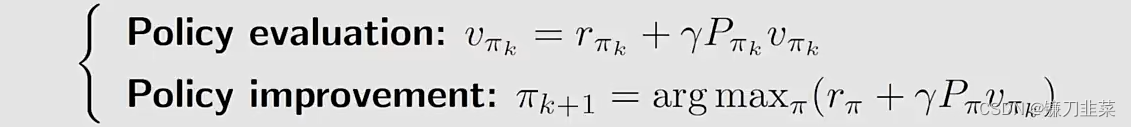
其中policy improvement step的elementwise form如下:
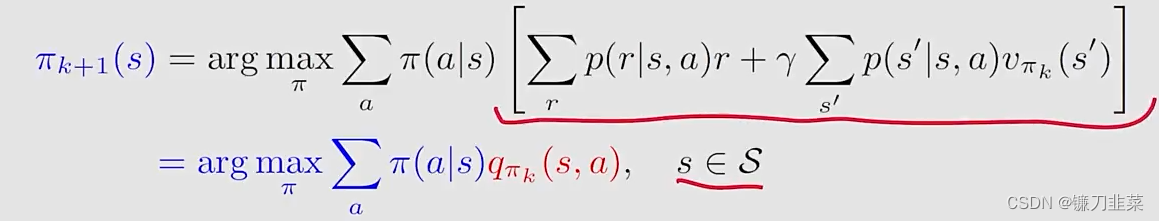
这里的关键是qπk(s,a)q_{\pi_k}(s, a)qπk(s,a)!计算qπk(s,a)q_{\pi_k}(s, a)qπk(s,a)有两种算法:
Expression 1 requires the model:
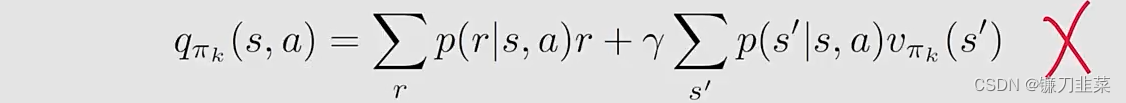
Expression 2 does not require the model:

上面的式子针对实现model-free的RL的启发是:可以使用式子2,根据数据(samples或者experiences)去计算qπk(s,a)q_{\pi_k}(s, a)qπk(s,a)。那具体是怎么做的呢?
The procedure of Monte Carlo estimation of action values:
- 首先,从一个组合(s,a)(s,a)(s,a)出发,按照一个策略πk\pi_kπk,生成一个episode;
- 计算这个episode,return是g(s,a)g(s, a)g(s,a)
- g(s,a)g(s,a)g(s,a)是在下式中GtG_tGt的一个采样:qπk(s,a)=E[Gt∣St=s,At=a]q_{\pi_k}(s,a)=\mathbb{E}[G_t|S_t=s, A_t=a]qπk(s,a)=E[Gt∣St=s,At=a]
- 假设我们有一组episodes和hence {g(j)(s,a)}\{g^{(j)}(s,a)\}{g(j)(s,a)},那么qπk(s,a)=E[Gt∣St=s,At=a]≈1N∑i=1Ng(i)(s,a)q_{\pi_k}(s,a)=\mathbb{E}[G_t|S_t=s, A_t=a]\approx \frac{1}{N}\sum_{i=1}^Ng^{(i)}(s, a)qπk(s,a)=E[Gt∣St=s,At=a]≈N1i=1∑Ng(i)(s,a)
所以,总的来说,一句话就是当我们没有模型的时候,我们要有数据,反正总得有一个。
到此时,算法也逐渐清晰,这个算法的名称是MC-Basic算法。下面描述这个算法:
给定一个初始策略π0\pi_0π0,在第k次迭代有两个步骤:
- Step 1:
policy evaluation

- Step 2:
policy improvemtn

第二步和policy iteration algorithm基本上是一致的,除了上式是直接估计qπk(s,a)q_{\pi_k}(s,a)qπk(s,a),而不是求解vπk(s)v_{\pi_k}(s)vπk(s)。
MC Basic algorithm(a model-free variant of policy iteration)的伪代码:

需要注意的是:
- MC Basic算法是policy iteration algorithm的一个变体。
- The model-free algorithms are built up based on model-based ones. 也就是说,在研究model-free算法之前,需要先了解对应的model-based算法。
- MC Basic是非常有用的,它可以揭示MC-based model-free RL的核心思想,但是它并不实用,因为它的efficiency比较低。
- 为什么MC Basic算法估计action values而不是state values?因为state values不能被用来直接改善policies。当模型不可用的时候,应该直接估计action values。
- 由于policy iteration是收敛的,那么很自然地,MC Basic的收敛性也保证了给定足够多的episodes后,它也是收敛的。
举个例子:step by step
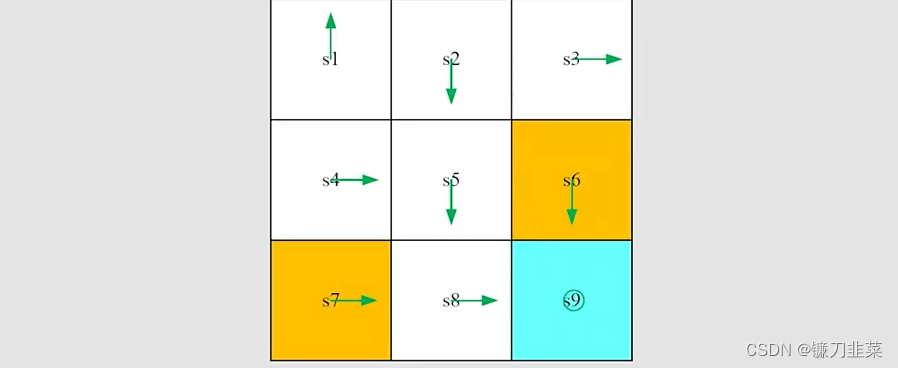
任务是:给定如图所示的一个初始策略,使用MC Basic算法找到一个最优策略,其中rboundary=−1,rforbidden=−1,rtarget=1,γ=0.9r_{boundary=-1}, r_{forbidden}=-1, r_{target}=1, \gamma=0.9rboundary=−1,rforbidden=−1,rtarget=1,γ=0.9。
MC Basic算法和policy iteration一样,也分为两步。给定当前策略πk\pi_kπk
- Step 1 ——policy evaluation: 计算qπk(s,a)q_{\pi_k}(s,a)qπk(s,a)。就这里而言,有多少个state-action pairs呢?一共有9 states × 5 actions =45 state-action pairs。
- Step 2 ——policy improvement: 选择greedy action a∗(s)=argmaxaiqπk(s,a)a^*(s)=arg\max_{a_i} q_{\pi_k}(s, a)a∗(s)=argaimaxqπk(s,a)
这里仅仅展示qπk(s1,a)q_{\pi_k}(s_1,a)qπk(s1,a):
Step 1-policy evaluation:
- 因为当前策略是确定性的,所以一个episode就可以得到action value!
- 如果当前策略是随机性的,就需要无限个episodes(至少要很多次)。
从(s1,a1)(s_1, a_1)(s1,a1)出发:

从(s1,a2)(s_1, a_2)(s1,a2)出发:

从(s1,a3)(s_1, a_3)(s1,a3)出发:

从(s1,a4)(s_1, a_4)(s1,a4)出发:

从(s1,a5)(s_1, a_5)(s1,a5)出发:

Step 2-policy improvement:
- 通过观察上面的action values,可以看到qπ0(s1,a2)=qπ0(s1,a3)q_{\pi_0}(s_1,a_2)=q_{\pi_0}(s_1,a_3)qπ0(s1,a2)=qπ0(s1,a3)是最大值。
- 因此,策略可以改进为π1(a2∣s1)=1or π1(a3∣s1)=1\pi_1(a_2|s_1)=1 \text{ or } \pi_1(a_3|s_1)=1π1(a2∣s1)=1 or π1(a3∣s1)=1
不管怎样,新的策略对于s1s_1s1是最优的。在这个例子中一次迭代就足够了。
举个例子2:Episode length
检查episode长度的影响:
- 需要采样episodes,但是the length of an episode cannot be infinitely long.
- 应该设置多长的episode?
示例设定:一个5-by-5的网格世界,奖励设定为:rboundary=−1,rforbidden=−1,rtarget=1,γ=0.9r_{boundary=-1}, r_{forbidden}=-1, r_{target}=1, \gamma=0.9rboundary=−1,rforbidden=−1,rtarget=1,γ=0.9
基于不同的episode长度,使用MC Basic去搜索最优策略:
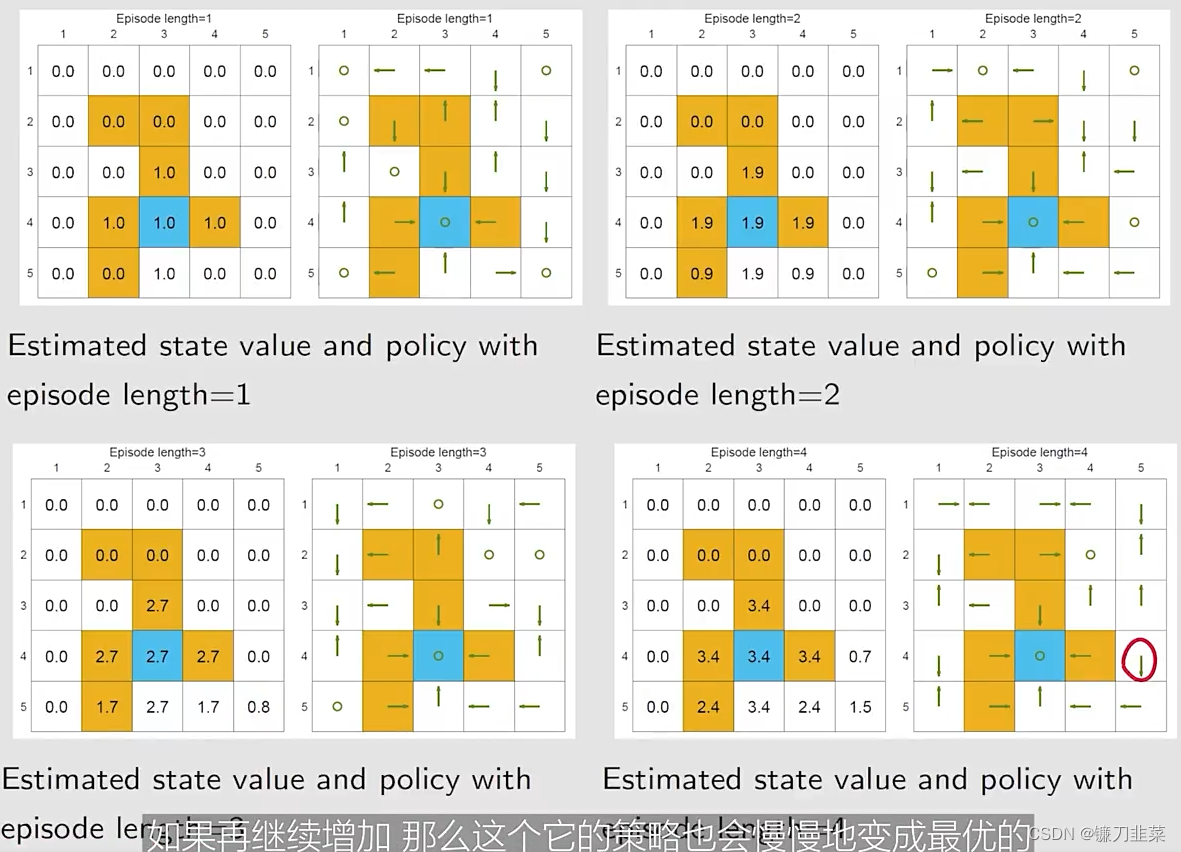
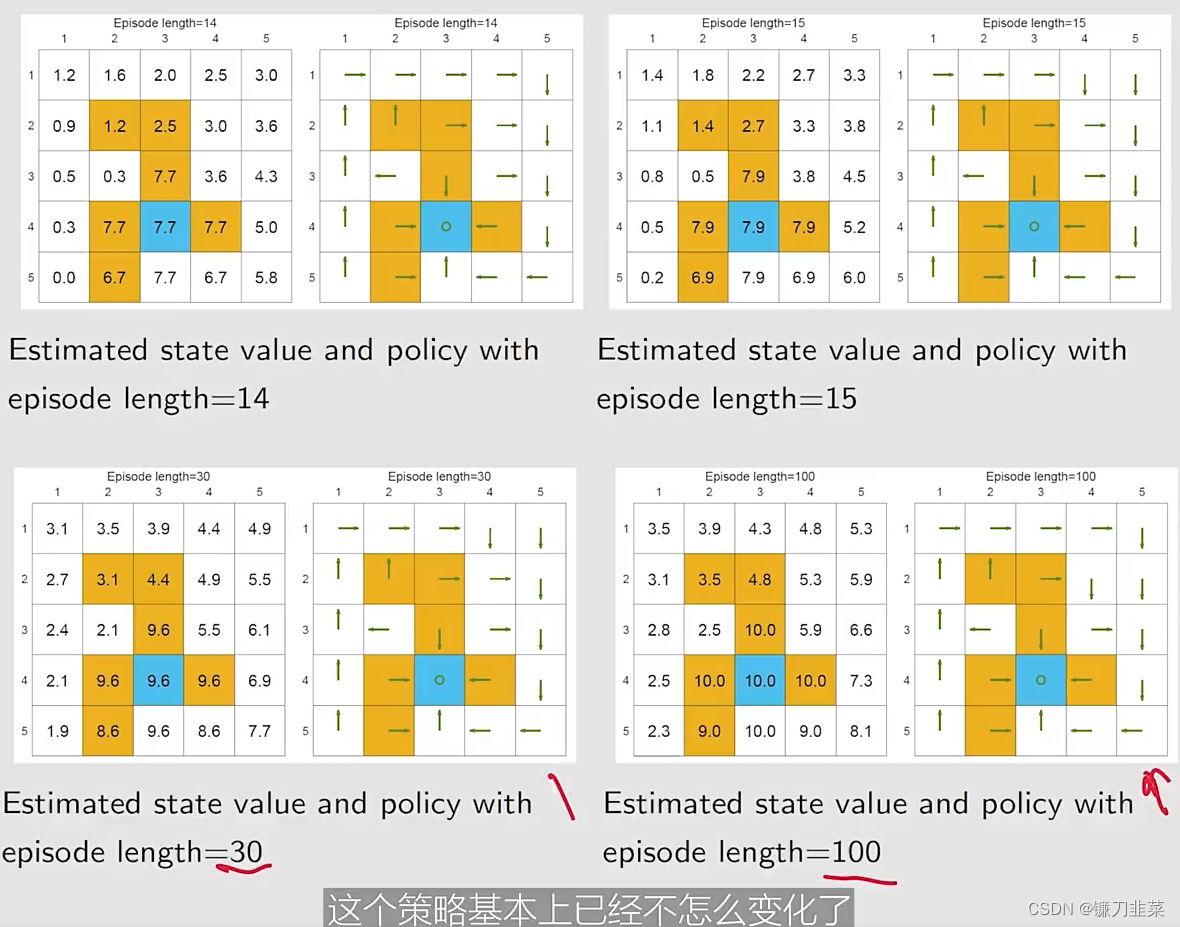
我们的发现:
- 当episode的长度较短的时候,只有离目标较近的状态具有非零的state values。
- 随着episode长度的增加,越靠近target的states更早地变为nonzero values,与那些与target较远的states相比。
- episode length必须要足够长
- episode length也不需要是无限长。
Use data more efficiently
MC Basic算法的优点是清晰地解释了MC方法的核心思想,但是缺点是太简单以至于无法在实际中使用。因此需要将MC Basic算法扩展,使其更加高效。那么如何来做呢?
首先,考虑一个网格世界,根据一个策略π\piπ,得到一个episode,如下:
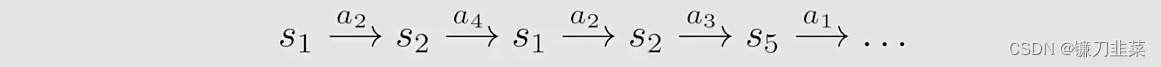
然后,引入一个概念,Visit:every time a state-action pair appears in the episode, it is called a visit of that state-action pair.
在MC Basic算法中用的一个策略是:Initial-visit method。
- 仅仅计算the return和估计qπ(s1,a2)q_{\pi}(s_1, a_2)qπ(s1,a2)
- 这也是MC Basic算法的做法
- 缺点是:不能完全利用数据
充分利用数据:The episode also visits other state-action pairs.

可以估计qπ(s1,a2)q_{\pi}(s_1, a_2)qπ(s1,a2), qπ(s2,a4)q_{\pi}(s_2, a_4)qπ(s2,a4), qπ(s2,a3)q_{\pi}(s_2, a_3)qπ(s2,a3), qπ(s5,a1)q_{\pi}(s_5, a_1)qπ(s5,a1)…
Data-efficient methods:
- first-visit method
- every-visit method
除了怎么样让数据的利用更加高效之外,Another aspect in MC-based RL is when to update the policy。 这里有两个方法:
- 第一种方法:

- 第二种方法:

那么问题来了,第二种方法会造成一些问题吗?
- 有人会认为一个episode的return不能准确估计相应的action value
- 事实上,we have done that in the truncated policy iteration algorithm,因此,就算不精确,也没有关系.
上述方法的名称是Generalized policy iteration, 简称为GPI:
- 它不是一个特定的具体的算法
- 它表示the general idea or framework of switching between policy-evaluation and policy-improvement processes.
- 许多model-based和model-free RL算法都能fall into this framework。
有了上面的过程,我们可以得到一个新的算法:Algorithm: MC Exploring Starts,即更加高效的使用数据和更新估计。

那么,为什么需要考虑exploring starts?
- 理论上,only if every action value for every state is well explored, can we select the optimal actions correctly. 相反,如果有一个action没有被explored, 那么可能会把这个action漏掉,而它刚好有可能是最优的。
- 实际上,exploring starts是非常难以实现的。对于许多应用,尤其是涉及和环境交互的物理场景中,难以从每一个state-action pair中收集episodes starting。
因此,在理论和实际中存在一个gap。那么能否将exploring starts这个条件去掉,或者转化掉,用其他的形式实现呢?答案是可以的,需要用到soft policies。
MC without exploring starts
什么是Soft policies?如果一个策略采取的每一个action的概率是positive,也就是这些action都有可能被采取,那么这个策略就称为soft。
那么为什么要引入soft policies呢?
- 基于soft policy,a few episodes that are sufficiently long can visit every state-action pair for sufficiently many times.
- Then,我们不需要从every state-action pair得到大量的episodes。因此,上一节中的exploring starts就可以被removed.
那么我们使用什么样的soft policies呢?答案是ϵ\epsilonϵ-greedy policies
什么是ϵ\epsilonϵ-greedy policy?

这里有一个性质,就是选择这个greedy action的概率始终比其他的任何一个action的概率都要大。
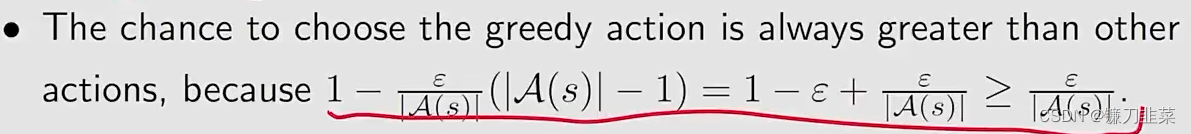
为什么要使用ϵ\epsilonϵ-greedy?因为它能够平衡exploitation(充分利用现有的)和exploration(探索未知的)。
- 当ϵ=0\epsilon = 0ϵ=0,它变为了greedy!与exploitation相比,exploration就会弱一些!
- 当ϵ=1\epsilon = 1ϵ=1,它变为了一个均匀分布,exploration更强,exploitation更弱。
那么如何将ϵ\epsilonϵ-greedy整合到MC-based RL算法中呢?
之前在MC Basic和MC Exploring Starts中policy improvement step是求解:
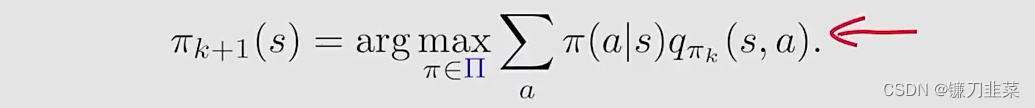
其中的Π\PiΠ表示所有可能的选择的集合。求解出来的最优的策略是:πk+1(a∣s)={1a=ak∗0a≠ak∗\pi_{k+1}(a|s)=\begin{cases}1 & a = a^*_k \\0 & a\ne a^*_k\end{cases}πk+1(a∣s)={10a=ak∗a=ak∗其中ak∗=argmaxaqπk(s,a)a^*_k=\text{arg}\max_aq_{\pi_k}(s,a)ak∗=argmaxaqπk(s,a)
现在,the policy improvement step变为求解:
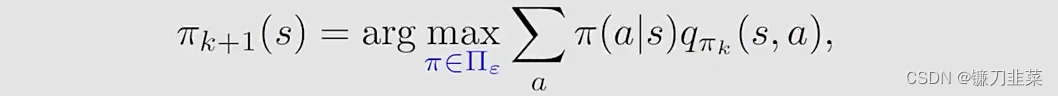
其中Πϵ\Pi_\epsilonΠϵ表示在一个固定的ϵ\epsilonϵ值条件下的所有ϵ\epsilonϵ-greedy policies的集合。这时得到的最优策略是
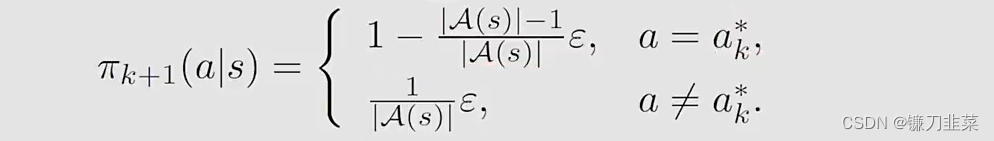
实际上,这里就得到了MC ϵ\epsilonϵ-greedy算法,与MC Exploring Starts算法相同,除了MC ϵ\epsilonϵ-greedy算法使用ϵ\epsilonϵ-greedy策略。因为使用这样一个策略,就不需要exploring starts这样的条件了,但是仍然要求visit all state-action pairs in a different form。
Algorithm: MC ϵ\epsilonϵ-Greedy的伪代码
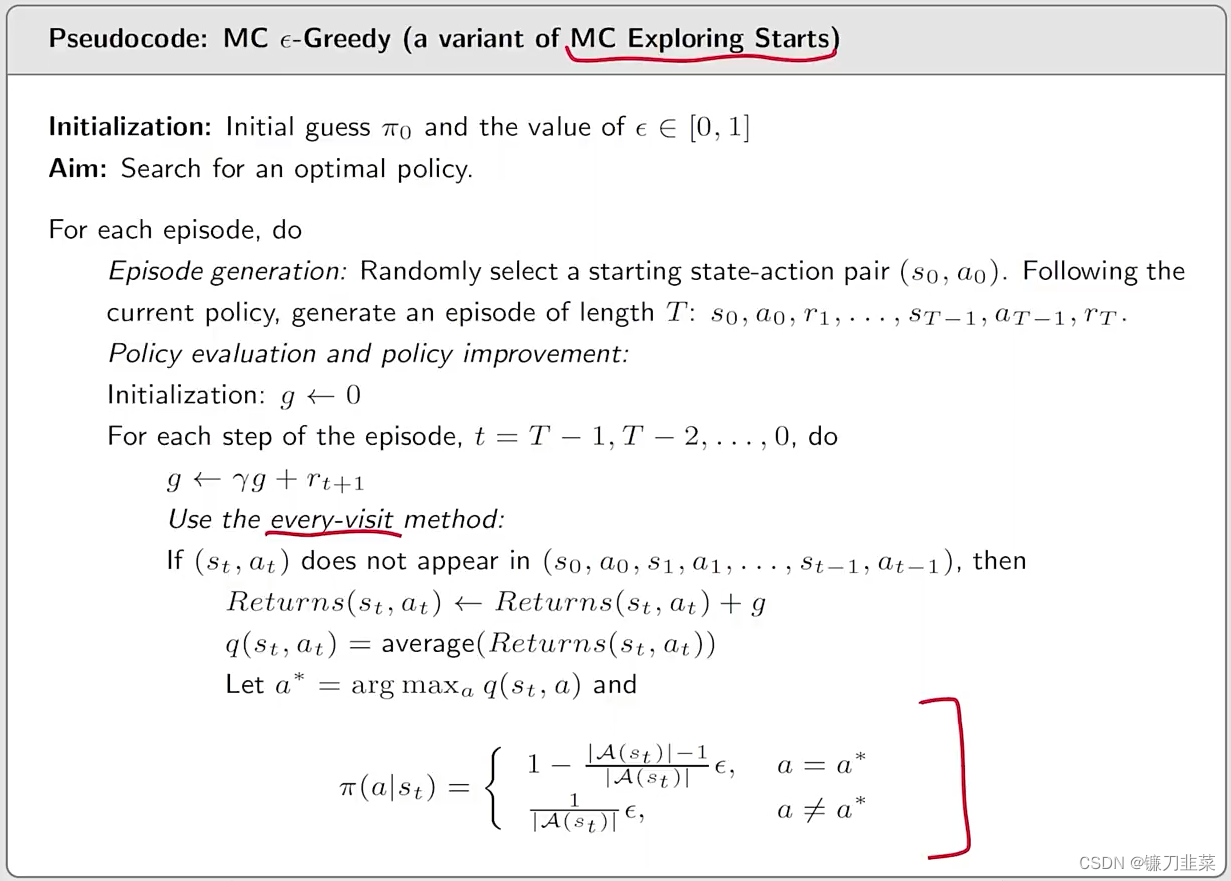
现在,我们分析该算法的探索能力,一个单独的episode可以visit所有的state-action pairs吗?
当ϵ=1\epsilon = 1ϵ=1,the policy(均匀分布)具有最强的探索能力。
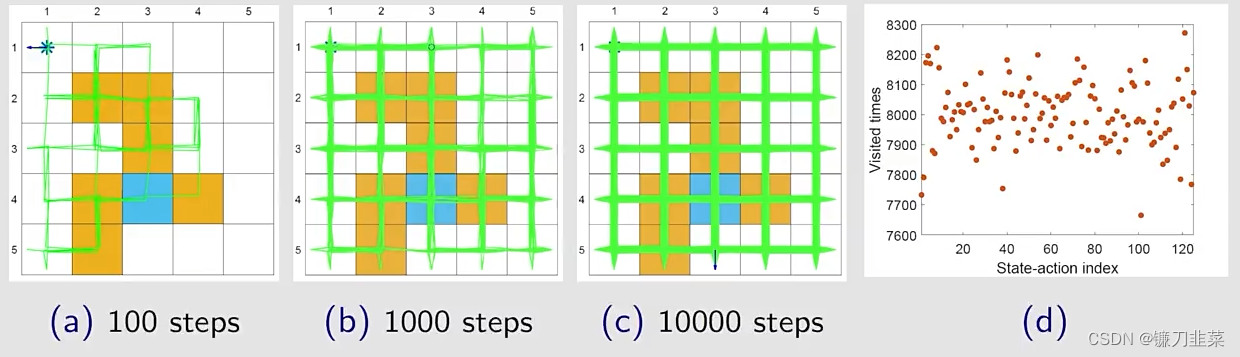
随着步数的增加,网格中几乎所有的位置都探索到了(绿色线),每个state-action被访问的次数也比较高。
当ϵ\epsilonϵ比较小的时候,策略的探索能力也会弱一些。
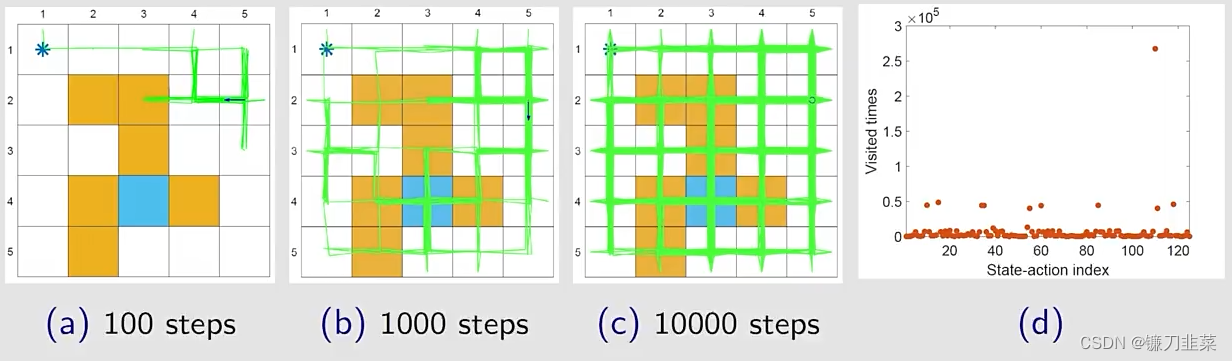
举个例子:利用ϵ\epsilonϵ-greedy结合蒙特卡洛算法,看一下这个算法能够带来什么样的最优策略。
在每一个iteration中:
- 在episode generation step,用当前的ϵ\epsilonϵ-greedy策略生成一个episode,这个episode非常长,只有100万步。
- 然后,用这一个episode去更新剩下所有的state-action pair和policy
- 这个算法避开了exploring starts这样一个条件,只要episode足够长,即使它从一个state-action pair出发,它仍然能够访问所有的其他的state-action pair。
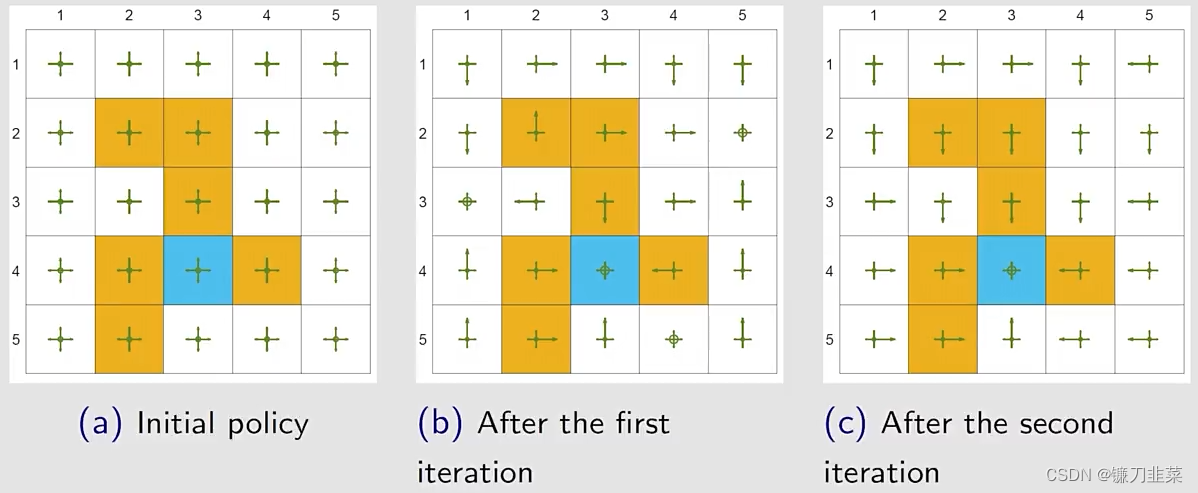
这里rboundary=−1,rforbidden=−10,rtarget=1,γ=0.9r_{boundary=-1}, r_{forbidden}=-10, r_{target}=1, \gamma=0.9rboundary=−1,rforbidden=−10,rtarget=1,γ=0.9,两次迭代就得到了一个optimal ϵ\epsilonϵ-greedy policy。所以ϵ\epsilonϵ-greedy通过探索性得到了一些好处,但是牺牲的是它的最优性。实际使用中,设置一个比较小的ϵ\epsilonϵ值,当它趋向于0的时候,ϵ\epsilonϵ-greedy接近于greedy,所以此时找到的最优的greedy的策略也就接近最优的greedy的策略。实际当中也可以让这个ϵ\epsilonϵ逐渐减小。

接下来,通过例子证明这个过程,设定为rboundary=−1,rforbidden=−10,rtarget=1,γ=0.9r_{boundary=-1}, r_{forbidden}=-10, r_{target}=1, \gamma=0.9rboundary=−1,rforbidden=−10,rtarget=1,γ=0.9。
最优性(Optimality):
给定一个ϵ\epsilonϵ-greedy policy,它的state value是什么?
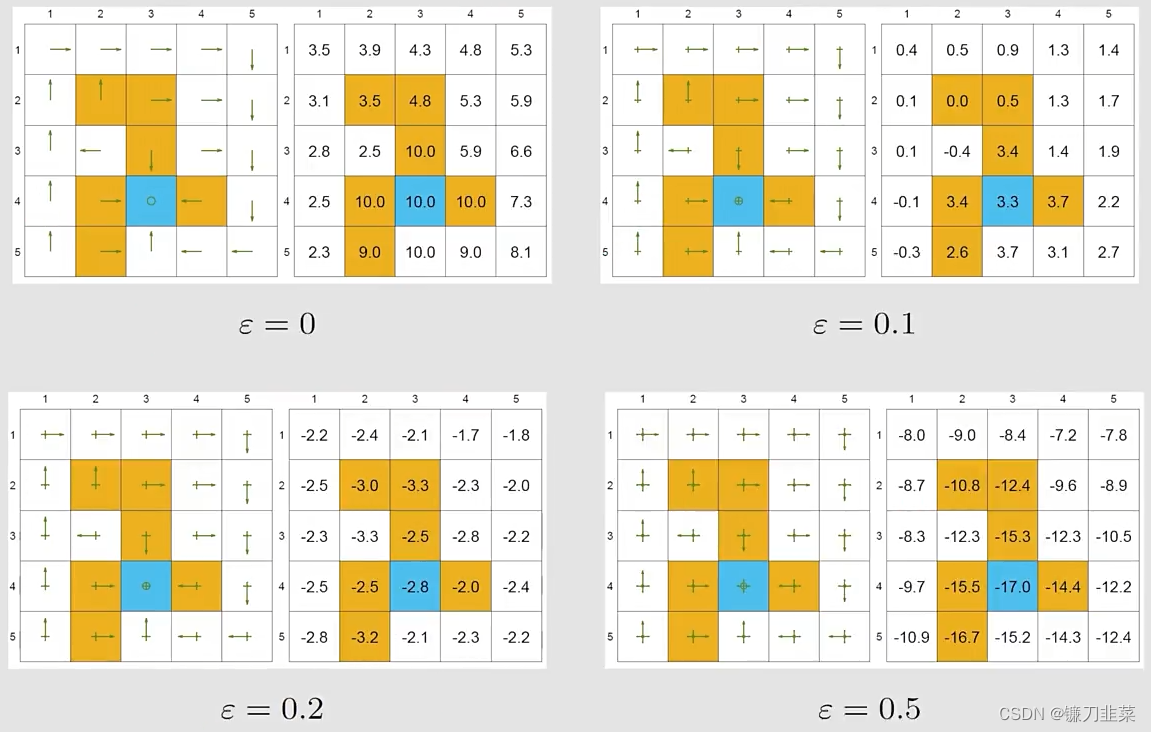
最优的策略就是有最大的state value的策略。当ϵ\epsilonϵ增加的时候,the optimality of the policy becomes worse! 为什么目标state的state value变为了negative?因为它在这个地方有比较大的概率进入到forbidden area,得到负数的reward会非常多。
一致性(Consistency):
找到最优的ϵ\epsilonϵ-greedy policies和它们的state values?直接给出一个最优策略,用MC ϵ\epsilonϵ-greedy 算法,设置ϵ\epsilonϵ为0.1。一致性也就是当ϵ\epsilonϵ-greedy得到的策略与greedy得到的策略是一致的。
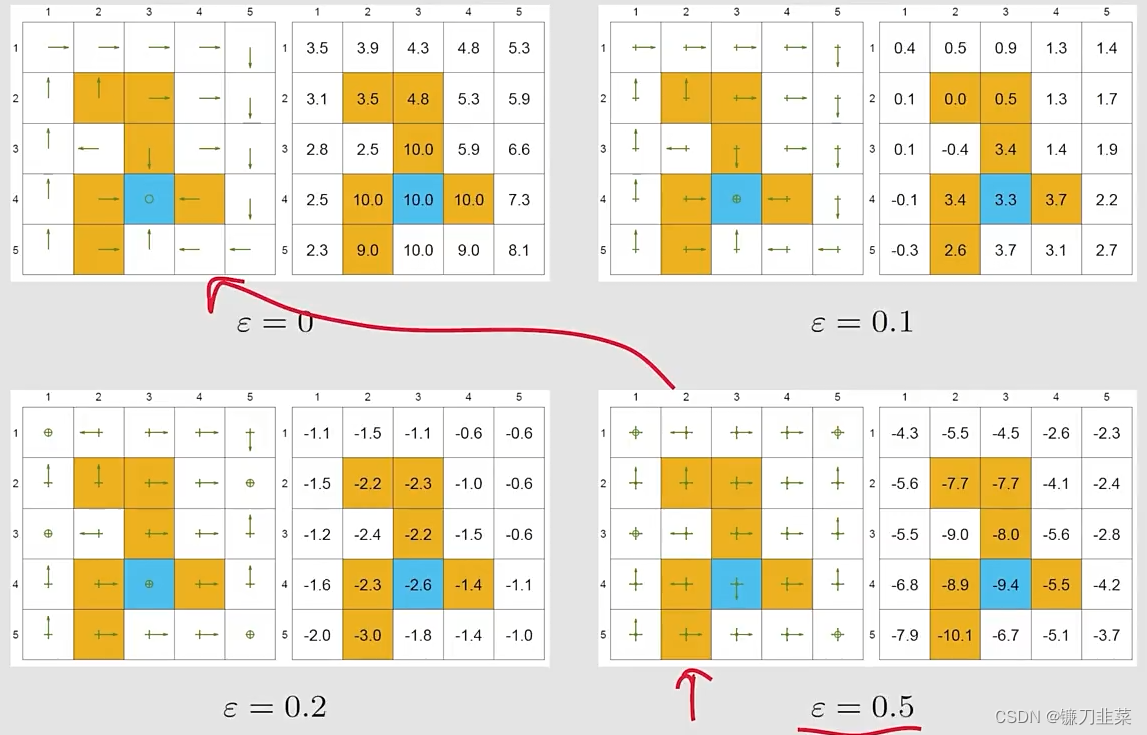
结论是如果想用 MC ϵ\epsilonϵ-greedy的时候,ϵ\epsilonϵ不能太大。从探索性比较大,逐步减小ϵ\epsilonϵ,最终得到一个最优的策略。
总结
关键点:
- 基于Monte Carlo方法的Mean estimation
- 三个算法:
- MC Basic
- MC Exploring Starts
- MC ϵ\epsilonϵ-Greedy
- 这三个算法之间的关系
- ϵ\epsilonϵ-greedy policies的最优性和探索性
内容来源
- 《强化学习的数学原理》 西湖大学工学院赵世钰教授
- 《动手学强化学习》 俞勇 著
相关文章:

【强化学习】强化学习数学基础:蒙特卡洛方法
强化学习数学方法:蒙特卡洛方法举个例子举个例子1:投掷硬币The simplest MC-based RL algorithm举个例子2:Episode lengthUse data more efficientlyMC without exploring starts总结内容来源将value iteration和policy iteration方法称为mod…...

BI分析工具软件有哪些
最近发现很多人讨论BI数据分析,今天给大家全面介绍下BI数据分析相关的信息。首先给大家科普一下,什么是BI分析。 BI分析其实是指通过BI分析工具,对企业内部和外部的大量数据进行收集、整理、处理和分析,以提供有价值的洞察&#x…...

2023爱分析·RPA软件市场厂商评估报告:容智信息
目录 1. 研究范围定义 2. RPA软件市场分析 3. 厂商评估:容智信息 4. 入选证书 1. 研究范围定义 RPA即Robotic Process Automation(机器人流程自动化),是一种通过模拟人与软件系统的交互过程,实现由软件机器人…...
——里氏替换原则、依赖倒转原则)
设计模式之七大原则(二)——里氏替换原则、依赖倒转原则
1.里氏替换原则 里氏替换原则(Liskov Substitution Principle,LSP)由麻省理工学院计算机科学实验室的里斯科夫女士在 1987 年的“面向对象技术的高峰会议”(OOPSLA)上发表的一篇文章《数据抽象和层次》)里提…...
 | 2023年2月刊)
数据库日常实操优质文章分享(含Oracle、MySQL等) | 2023年2月刊
本文为大家整理了墨天轮数据社区2023年2月发布的优质技术文章,主题涵盖Oracle、MySQL、PostgreSQL等数据库的环境搭建、故障处理等日常实践操作,以及概念梳理、常用脚本等总结记录,分享给大家:Oracle优质技术文章概念梳理&基础…...

事件循环机制(Event Loop)和宏任务(macro-tast)微任务(micro-tast),详细讲解!!!
“事件循环机制” 和 “宏任务微任务” 也是前端面试中常考的面试题了。首先,要深刻理解这些概念的话,需要回顾一些知识点。知识点回顾1、进程与线程进程。 程序运行需要有它自己的专属内存空间,可以把这块内存空间简单的理解为进程每个应用至…...

mysql基础操作3
查询襄阳的员工姓名和性别,性别要求显示为 男 女SELECT ename,(CASE WHEN sexF THEN 女 ELSE 男 END)sexFROM empWHERE jiguan襄阳查询所有的订单,显示订单日期 订单数量 订单状态SELECT saleDate,salesQuantity,(CASE WHEN saleState1 THEN 新建 WHEN s…...

【Web安全】PHP安全
一、文件包含漏洞严格来说,文件包含就是代码注入的一种。代码注入,其原理就是注入一段用户能控制的脚本或代码并让服务器端执行。代码注入的典型代表就是文件包含。文件包含可能会出现在JSP、PHP、ASP等语言中,常见函数如下:PHP&a…...

双向链表+循环链表
循环链表双向链表 循环链表 循环链表是头尾相接的链表(即表中最后一个结点的指针域指向头结点,整个链表形成一个环)(circular linked list) **优点:**从表中任一结点出发均可访问全部结点 循环链表与单链表的主要差别当链表遍历时,判别当前…...
Java程序的逻辑控制
一、顺序结构 顺序结构比较简单,如果我们按照代码书写的顺序一行一行执行,将会是这样的: System.out.println("aaa"); System.out.println("bbb"); System.out.println("ccc"); // 运行结果 aaa bbb ccc 如…...

BUCTOJ - 2023上半年ACM蓝桥杯每周训练题-1-A~K题C++Python双语版
文章目录BUCTOJ - 2023上半年ACM&蓝桥杯每周训练题-1-A~K题CPython双语版前言问题 A: 1.2 神奇兔子数列题目描述输入输出解题思路AC代码CPython问题 B: 1.3 马克思手稿中的数学题题目描述输入输出解题思路AC代码CPython问题 C: 1.4 爱因斯坦的阶梯题目描述输入输出解题思路…...
存储的本质-学习笔记
1 经典案例 1.1 数据的流动 一条用户注册数据流动到后端服务器,持久化保存到数据库中。 1.2 数据的持久化 校验数据的合法性修改内存写入存储介质2 存储&数据库简介 2.1 存储系统特点 性能敏感、容易受硬件影响、存储系统代码既“简单”又“复杂”。 2.2 数…...

新一代骨传导机皇重磅发布:南卡Neo骨传导运动耳机,性能全面提升
近日,中国最强骨传导品牌NANK南卡发布了最新一代骨传导耳机——南卡Neo骨传导耳机!该款耳机与运动专业性更强的南卡runner Pro4略微不同,其主要定位于轻运动风格,所以这款耳机的音质和佩戴舒适度达到了令人咂舌的地步!…...

Hbase Schema设计与数据模型操作
一、Hbase Schema设计 1,Schema 创建 使用 Apache HBase Shell 或使用 Java API 中的 Admin 来创建或更新 HBase 模式。 Configuration config HBaseConfiguration.create(); Admin admin new Admin(conf); TableName table TableName.valueOf("myTable&…...

微电影广告有哪些传播优势?
微电影广告是在基于微电影的模式下发展而来的,是伴随着当下快节奏、碎片化的生活方式而诞生的新兴广告表现形式。微电影广告凭借其具备的独特传播优势以及时代特征成为广大企业主塑造企业品牌形象的主要方式。那么,微电影广告究竟有哪些传播优势…...
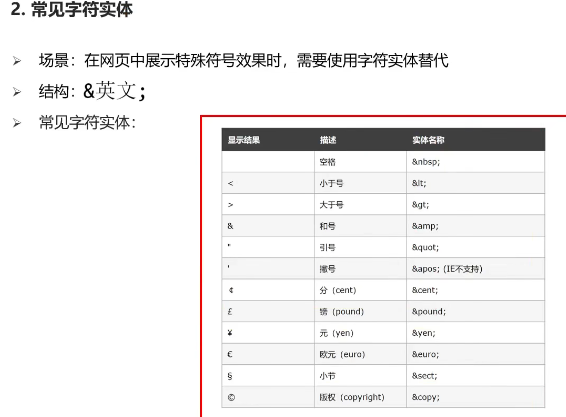
html基础(列表(ul、ol、dl)、表格table、表单(input、button、label)、div和span、空格nbsp)
1无序列表<ul>和有序列表<ol>1.1无序列表<ul><!-- 无序列表 --><ul><li>吃饭</li><li>睡觉</li><li>打豆豆</li></ul>1.2有序列表<ol><!-- 有序列表 --><ol><li>吃饭</li…...

uniapp常用标签
view ~~ 视图容器类似于传统html中的div,用于包裹各种元素内容<view><text>hh</text> </view>scroll-view ~~可滚动视图区域scroll-x 允许横向滚动scroll-y 允许纵向滚动scroll-top 设置竖向滚动条位置,可以一键回到顶部refresh…...

《数字中国建设整体布局规划》发布,推进IPv6部署和应用是重点
近日,中共中央、国务院印发了《数字中国建设整体布局规划》(以下简称《规划》),并发出通知,要求各地区各部门结合实际认真贯彻落实。 《规划》指出,建设数字中国是数字时代推进中国式现代化的重要引擎&…...
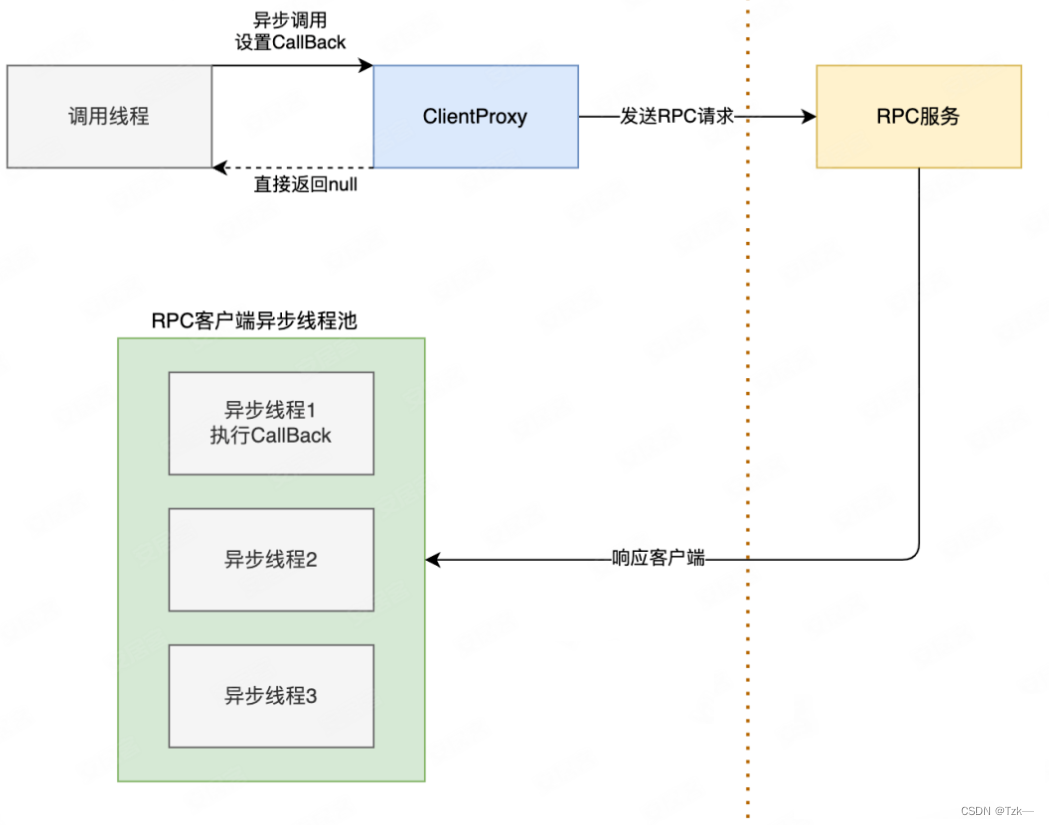
【Java】 异步调用实践
本文要点: 为什么需要异步调用CompletableFuture 基本使用RPC 异步调用HTTP 异步调用编排 CompletableFuture 提高吞吐量BIO 模型 当用户进程调用了recvfrom 这个系统调用,kernel 就开始了 IO 的第一个阶段:准备数据。对于 network io 来说…...
园区智慧能源管理系统
实现对园区的用能情况实时、全方位监测,重点设备进行数据自动采集并智能统计、分析,根据需要绘制各种趋势曲线、能源流向图和分析报表。将物联网、大数据与全过程能源管理相融合,提供全生命周期的数字化用能服务,实现用能的精细化…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...
