java数据结构与算法刷题-----LeetCode70. 爬楼梯
| java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 |
|---|
很多人觉得动态规划很难,但它就是固定套路而已。其实动态规划只不过是将多余的步骤,提前放到dp数组中(就是一个数组,只不过大家都叫它dp),达到空间换时间的效果。它仅仅只是一种优化思路,因此它目前的境地和线性代数一样----虚假的难。
- 想想线性代数,在国外留学的学生大多数不觉得线性代数难理解。但是中国的学生学习线性代数时,完全摸不着头脑,一上来就是行列式和矩阵,根本不知道这玩意是干嘛的。
- 线性代数从根本上是在空间上研究向量,抽象上研究线性关系的学科。人家国外的教科书都是第一讲就帮助大家理解研究向量和线性关系。
- 反观国内的教材,直接把行列式搞到第一章。搞的国内的学生在学习线性代数的时候,只会觉得一知半解,觉得麻烦,完全不知道这玩意学来干什么。当苦尽甘来终于理解线性代数时干什么的时候,发现人家国外的教材第一节就把这玩意讲清楚了。你只会大骂我们国内这些教材,什么狗东西(以上是自己学完线性代数后的吐槽,我们同学无一例外都这么觉得)。
而我想告诉你,动态规划和线性代数一样,我学完了才知道,它不过就是研究空间换时间,提前将固定的重复操作规划到dp数组中,而不用暴力求解,从而让效率极大提升。
- 但是网上教动态规划的兄弟们,你直接给一个动态方程是怎么回事?和线性代数,一上来就教行列式和矩阵一样,纯属恶心人。我差不多做了30多道动态规划题目,才理解,动态方程只是一个步骤而已,而这已经浪费我很长时间了,我每道题都一知半解不理解,过程及其痛苦。最后只能重新做。
- 动态规划,一定是优先考虑重复操作与dp数组之间的关系,搞清楚后,再提出动态方程。而你们前面步骤省略了不讲,一上来给个方程,不是纯属扯淡吗?
- 我推荐研究动态规划题目,按5个步骤,从上到下依次来分析
- DP数组及下标含义
- 递推公式
- dp数组初始化
- 数组遍历顺序(双重循环及以上时,才考虑)
- dp数组打印,分析思路是否正确(相当于做完题,检查一下)
| 拿到比较抽象的题,先列出前几项结果,尝试看出问题的本质(很多比较抽象的题,本质都很简单,抓住问题的本质,那么可以做到解决1道题,扩展到解决一类问题) |
|---|
- n = 0时:结果为0
- n = 1时:结果为1
- n = 2时:结果为2
- n = 3时:结果为3
- n = 4时:结果为5
可见 这道题的规律0 1 2 3 5… 和斐波那契数列的0 1 1 2 3 5…非常像
| 什么是斐波那契数列? |
|---|
- 斐波那契数列:第一个值是0,第二个值是1,剩下的元素是它前两个元素和,例如:0 1 1 2 3 5… , 可见除了最开始的两个固定为0和1外,其余每一个元素都是前两个元素的和。
- 也就是说,这玩意一看就是固定的一套值,如果每次都重新生成,就太暴力了。
- 动态规划的思想就是,将生成的过程,就生成一次,之后再用,直接从dp数组中拿。从而大大提升效率
| 解题思路 |
|---|
- 暴力求解的思想,就是定义3个或者2个变量,然后累加,以获得指定位置的斐波那契数。每次都需要从头开始累加
- 但是如果我们预先将其存储到dp数组,就可以直接通过dp[x], 获取dp数组中指定位置x的对应斐波那契数,而不用每次都从头计算。
- 但是这道题,从第4个元素开始,才符合斐波那契数列的规则,因此我们这道题,可以用斐波那契数列思想,但不能照搬
- 可见这道题,前3个为固定值 0 1 2 ,剩下的都是当前元素的前两项的和。
| 动态规划思考5步曲 |
|---|
- DP数组及下标含义
DP数组存储我们分析的
类似斐波那契数列的数列,这个数列是一维线性的,所以只需一维数组存储。下标代表数在数列中的位置。dp[0] = 0,dp[1] = 1,dp[2]=2是头三个固定值(斐波那契数列头两个是固定值),dp[3]开始,每个元素是前两个数组元素的和。即可生成对应数列的dp数组。
- 递推公式
既然知道了DP数组就是存储的
类似斐波那契数列的数列,那么递推公式,很显然就是当前元素=前两个元素的和。F(n) = F(n-1)+F(n-2)。 而且F(0) = 0,F(1)=1,F(2) = 2这是这个数列的特性,前三个值固定为0,1,2.
- dp数组初始化
- 数组遍历顺序(因为这个数列是一维的,只需要一重循环,无需考虑这个)
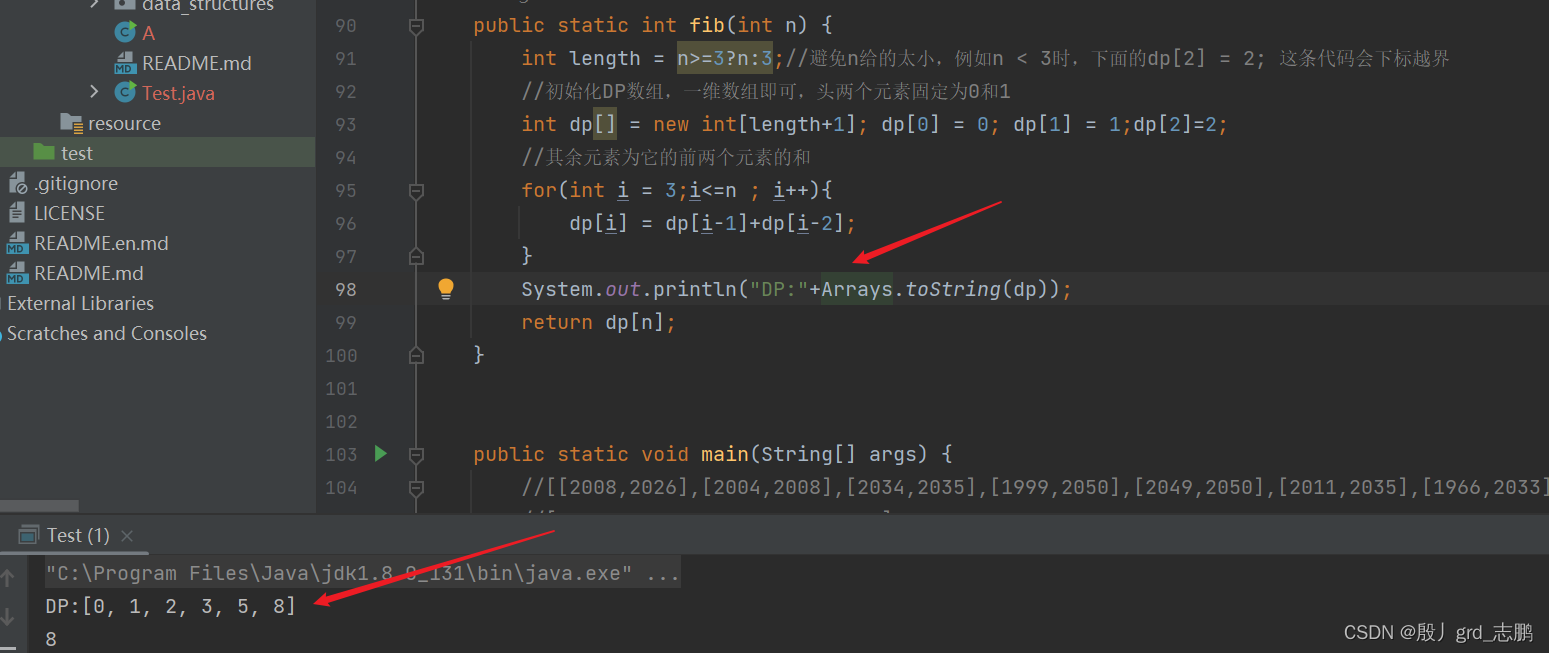
- 打印dp数组(自己生成dp数组后,将dp数组输出看看,是否和自己预想的一样。)
| 代码 |
|---|
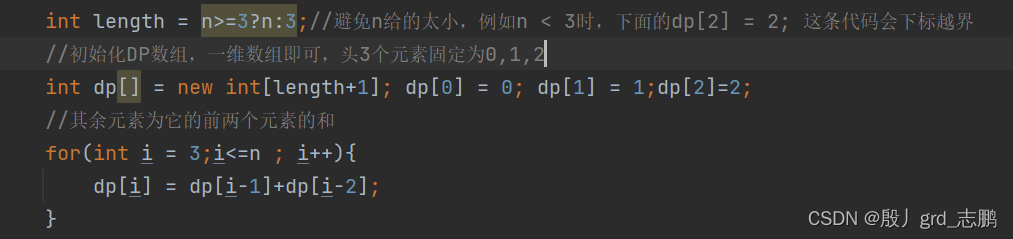
class Solution {public int climbStairs(int n) {int length = n>=3?n:3;//避免n给的太小,例如n < 3时,下面的dp[2] = 2; 这条代码会下标越界//初始化DP数组,一维数组即可,头3个元素固定为0,1,2int dp[] = new int[length+1]; dp[0] = 0; dp[1] = 1;dp[2]=2;//其余元素为它的前两个元素的和for(int i = 3;i<=n ; i++){dp[i] = dp[i-1]+dp[i-2];}return dp[n];}
}
相关文章:
java数据结构与算法刷题-----LeetCode70. 爬楼梯
java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 很多人觉得动态规划很难,但它就是固定套路而已。其实动态规划只…...
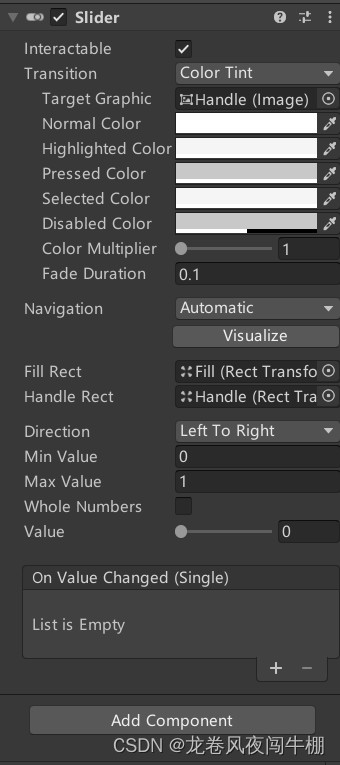
【Unity入门】UGUI之Slider(滑动条)
目录 一、什么是Slider?二、Slider属性与功能 一、什么是Slider? Slider控件允许用户可以通过鼠标来在预先确定的范围调节数值 我们可以在Hierarchy视图右键 -> UI ->Slider来创建滑动条 通过上图可以发现Unity内置的Slider主要有3部分&#x…...

MySQL中UNION和UNION ALL的区别有哪些?
在MySQL中如何想要对两个结果集进行合并操作,可以使用UNION和UNION ALL,如果只是想要去除掉重复的记录,属于UNION ALL 即可,但是如何想要除掉没有重复行数据,就要使用Union。本文详细向大家介绍MySQL中UNION和UNION AL…...
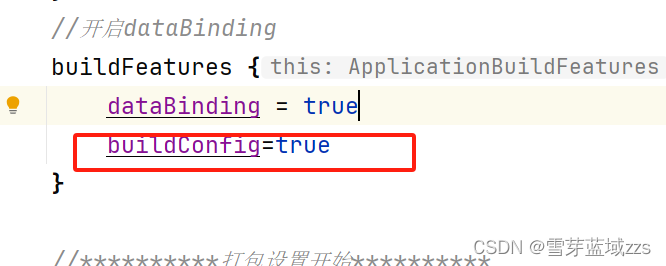
Android kotlin build.gradle.kts配置
1. 添加 maven 仓库 1. 1. settings配置 1. 1.1. settings.gradle repositories {maven {url https://maven.aliyun.com/repository/public/}mavenCentral() }1. 1.2. settings.gradle.kts repositories {maven {setUrl("https://maven.aliyun.com/repository/public/…...

css、js、vue常考部分面试题
css css盒子水平垂直居中方法 方法一:定位 .child{height: 100px;position: absolute;//父元素相对定位top:50%;left:50%;transform: translate(-50%,-50%); } 方法二:定位 .child{width: 100px;height: 100px;position: absolute;top:50%;left:50%…...

OpenAI ChatGPT-4开发笔记2024-03:Chat之Function Calling/Function/Tool/Tool_Choice
Updates on Function Calling were a major highlight at OpenAI DevDay. In another world,原来的function call都不再正常工作了,必须全部重写。 function和function call全部由tool和tool_choice取代。2023年11月之前关于function call的代码都准备翘翘。 干嘛…...
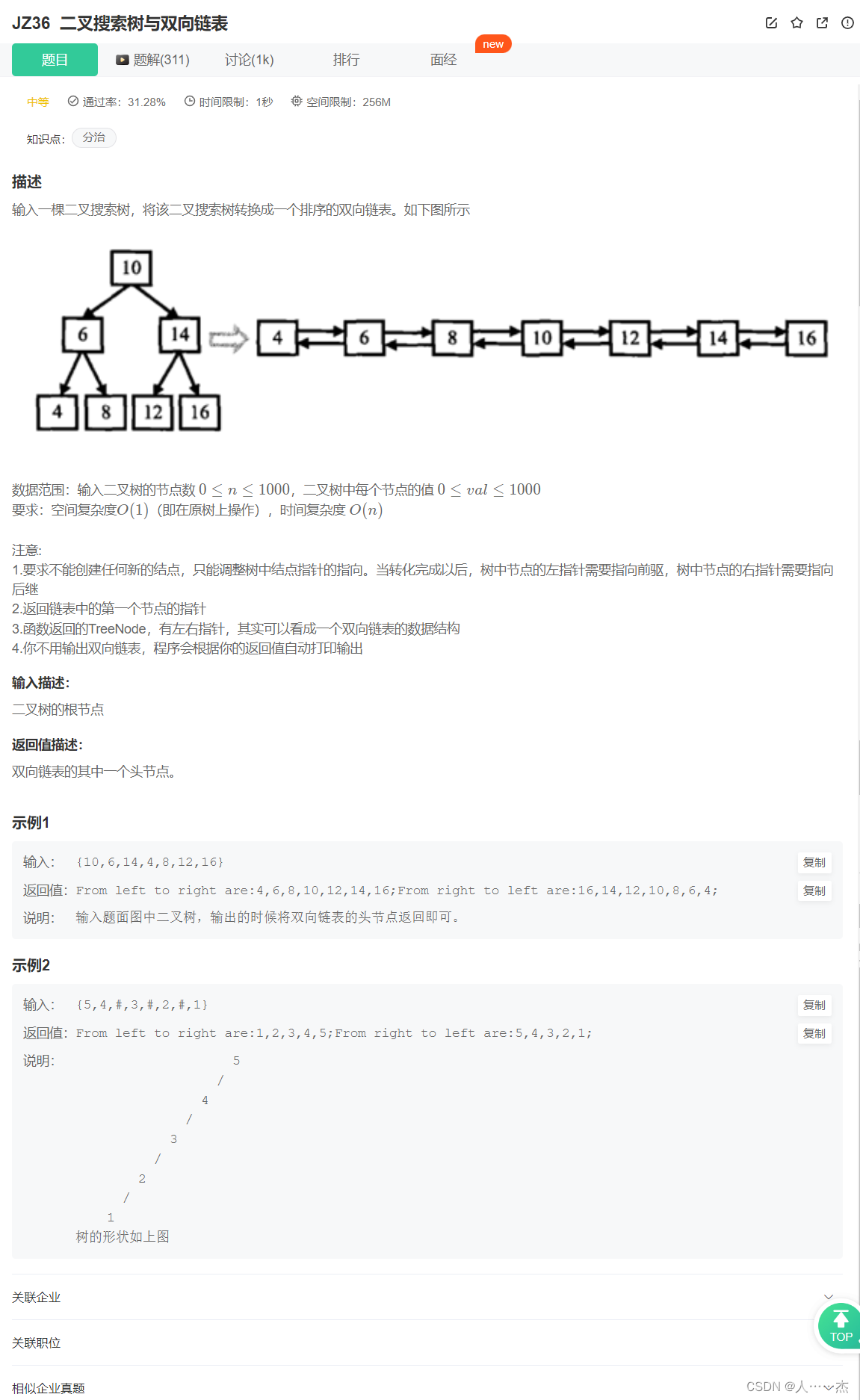
二叉搜索树与双向链表
解题思路一: /** public class TreeNode {int val 0;TreeNode left null;TreeNode right null;public TreeNode(int val) {this.val val;} } */ // 一定要用自己的理解真正弄出来才行,否则没有用! // 再次提醒,计算机这种工科…...

uniapp中组件库的Checkbox 复选框 的丰富使用方法
目录 #平台差异说明 #基本使用 #自定义形状 #禁用checkbox #自定义形状 #自定义颜色 #横向排列形式 #横向两端排列形式 API #Checkbox Props #CheckboxGroup Props #CheckboxGroup Event 复选框组件一般用于需要多个选择的场景,该组件功能完整ÿ…...
Spring Cloud + Vue前后端分离-第10章 基于阿里云OSS的文件上传
源代码在GitHub - 629y/course: Spring Cloud Vue前后端分离-在线课程 Spring Cloud Vue前后端分离-第10章 基于阿里云OSS的文件上传 前面介绍的文件上传是基于本地文件服务器的文件上传,但是自己搭文件服务器会有很多运维的问题,比如磁盘满了要扩容…...

C++ 中的耗时计算函数
#include <time.h>int clock_gettime (clockid_t clock_id, struct timespec *tp) 获取当前 clock_id 的时钟值并存储在 tp 中。 其中 tp 是一个 timespec 结构体,在 time.h 头文件中定义: #include <time.h>:struct timespec {time_t t…...

【Element】el-form和el-table嵌套实现表格编辑并提交表单校验
一、背景 页面需要用到表格采集用户数据,提交时进行表单校验;即表格中嵌套着表单,保存时进行表单校验 二、功能实现 2.1、el-form和el-table嵌套说明 ① :model"formData" 给表单绑定数据,formData是表单的数据对象 …...

初识Winform
什么是winform? WinForms(Windows Forms)是Microsoft .NET框架中的一个用户界面(UI)技术,用于创建Windows应用程序。它提供了一组用于构建图形用户界面的类和控件,以及与用户交互的事件模型。 …...

Redis:原理速成+项目实战——Redis实战5(互斥锁、逻辑过期解决缓存击穿问题)
👨🎓作者简介:一位大四、研0学生,正在努力准备大四暑假的实习 🌌上期文章:Redis:原理速成项目实战——Redis实战4(解决Redis缓存穿透、雪崩、击穿) 📚订阅专…...

前端优化之一:dns预获取 dns-prefetch 提升页面载入速度
问题:怎么做到dns域解析? 用于优化网站页面的图片 问题:怎么提升网站性能? dns域解析,是提升网站的一个办法。 DNS Prefetch,即DNS预获取,是前端优化的一部分。 一般来说,在前端…...

C语言中一些基本数据类型的典型大小
char:通常是1字节。表示一个字符。int:通常在现代系统中是4字节(但这取决于编译器和架构,有时可能是2字节)。float:通常是4字节。double:通常是8字节。short 和 short int:通常是2字…...
[C/C++]排序算法 快速排序 (递归与非递归)
目录 🚩概念: 🚩实现: ⚡1.hoare ⚡2.挖坑法 ⚡3.双指针法 🚩快速排序递归实现 🚩快速排序非递归实现 🚩概念: 通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据比另一部分的所有…...

『年度总结』逐梦编程之始:我的2023学习回顾与展望
目录 前言 我与Python 我与C语言 第一篇正式博客: 第二篇正式博客(扫雷): 指针学习笔记: C语言学习笔记: 我与数据结构: yuan 这篇博客,我将回顾2023年编程之旅的起点,同时展…...
MyBatis学习二:Mapper代理开发、配置文件完成增删改查、注解开发
前言 公司要求没办法,前端也要了解一下后端知识,这里记录一下自己的学习 学习教程:黑马mybatis教程全套视频教程,2天Mybatis框架从入门到精通 文档: https://mybatis.net.cn/index.html Mapper代理开发 目的 解决…...
【React系列】受控非受控组件
本文来自#React系列教程:https://mp.weixin.qq.com/mp/appmsgalbum?__bizMzg5MDAzNzkwNA&actiongetalbum&album_id1566025152667107329) 一. refs 的使用 在React的开发模式中,通常情况下不需要、也不建议直接操作DOM原生,但是某些…...
:2D直方图)
OpenCV-Python(22):2D直方图
目标 了解图像的2D直方图绘制2D直方图 介绍 在前面的部分我们介绍了如何绘制一维直方图,之所以称为一维,是因为我们只考虑了图像的一个特征:灰度值。但是在2D 直方图中我们就需要考虑两个图像特征。对于彩色图像的直方图通常情况下我们需要…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...

何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡
何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡 背景 我们以建设星云智控官网来做AI编程实践,很多人以为AI已经强大到不需要程序员了,其实不是,AI更加需要程序员,普通人…...
C++11 constexpr和字面类型:从入门到精通
文章目录 引言一、constexpr的基本概念与使用1.1 constexpr的定义与作用1.2 constexpr变量1.3 constexpr函数1.4 constexpr在类构造函数中的应用1.5 constexpr的优势 二、字面类型的基本概念与使用2.1 字面类型的定义与作用2.2 字面类型的应用场景2.2.1 常量定义2.2.2 模板参数…...

【汇编逆向系列】六、函数调用包含多个参数之多个整型-参数压栈顺序,rcx,rdx,r8,r9寄存器
从本章节开始,进入到函数有多个参数的情况,前面几个章节中介绍了整型和浮点型使用了不同的寄存器在进行函数传参,ECX是整型的第一个参数的寄存器,那么多个参数的情况下函数如何传参,下面展开介绍参数为整型时候的几种情…...