Bagging算法_随机森林Random_Forest
Bagging
B a g g i n g Bagging Bagging是并行式集成学习方法最著名的代表,这个名字是由 B o o t s t r a p A G G r e g a t I N G Bootstrap AGGregatING BootstrapAGGregatING而来,顾名思义,该算法由 B o o s t s t r a p Booststrap Booststrap与 A g g r e g a t i n g Aggregating Aggregating两部分组成。
欲得到泛化性能强的集成,集成中的个体学习器应尽可能相互独立,一种可能的做法是对训练样本进行采样,产生若干不同的子集,再从每个数据子集中训练处一个学习器。同时,为了获得更好的集成,每个个体学习器不能太差。如果每次采样出的子集都完全不同,则每个基学习器只用到了一小部分训练数据,甚至不足以进行有效学习,这显然无法确保产生出比较好的基学习器。
B a g g i n g Bagging Bagging为解决这个问题,使用自助取样( B o o t s t r a p i n g Bootstraping Bootstraping)。给定包含 m m m个样本的数据集,我们先随机取出一个样本放入采样集中,再将该样本放回初始数据集,使得下次采样时该样本仍有可能被选中,这样,经过 m m m次随机采样操作,我们得到含 m m m个样本的采样集,初始训练集中有的样本在采样集里多次出现,有的则从未出现,可以做一个简单的估计,样本在 m m m次采样中始终不被采到的概率是 ( 1 − 1 m ) m {(1-\frac{1}{m})}^m (1−m1)m,求极限得到:
lim m → ∞ ( 1 − 1 m ) m → 1 e ≈ 0.368 \lim_{m \to \infty }{(1-\frac{1}{m} )}^m \to \frac{1}{e} \approx 0.368 m→∞lim(1−m1)m→e1≈0.368
可知,初始训练集中约有 63.2 % 63.2\% 63.2%的样本出现在采样集中。
算法:
设有一个大小为 N N N的训练数据集,每次从该数据集中有放回的选出大小为 M M M的子数据集,一共选 K K K次;
根据这 K K K个子数据集,训练学习出 K K K个模型;
使用这 K K K个模型进行预测,再通过取平均值或者多数分类的方式,得到最后的预测结果。
随机森林 Random Forest
随机森林简称 R F RF RF,是以决策树为估计器的 B a g g i n g Bagging Bagging算法。
算法:
假设训练集 T T T的大小为 N N N,特征数为 M M M,随机森林的大小为 K K K;
遍历 R F RF RF的大小 K K K次:
从训练集T中有放回抽样的方式,取样 N N N次形成一个新子训练集 D D D;
随机选择 m m m个特征,其中 m < M m<M m<M;
使用新的训练集 D D D和 m m m个特征,学习出一个完整的决策树
得到随机森林。
RF的优点
- 针对很多任务可以产生高准确度的分类器;
- 可以处理大量的输入变量;
- 可以在决定类别时,给出变量的重要性;
- 在建造森林时,可以在内部对于一般化后的误差产生不偏差的估计;
- 包含一个好方法可以估计丢失的资料,并且如果有很大一部分的资料丢失,仍可以维持准确度;
- 对于不平衡的分类资料集来说,可以平衡误差;
- 可被延伸应用在未标记的资料上,这类资料通常是使用非监督式聚类,也可以侦测偏离者和观看资料;
- 学习过程很快速。
RF的缺点
- 不可解释性;
- 在噪音较大的任务上会过拟合;
- 在多分类任务中,RF可能无法提高基学习器的准确性。
相关文章:

Bagging算法_随机森林Random_Forest
Bagging B a g g i n g Bagging Bagging是并行式集成学习方法最著名的代表,这个名字是由 B o o t s t r a p A G G r e g a t I N G Bootstrap AGGregatING BootstrapAGGregatING而来,顾名思义,该算法由 B o o s t s t r a p Booststrap Boos…...
物理与网络安全
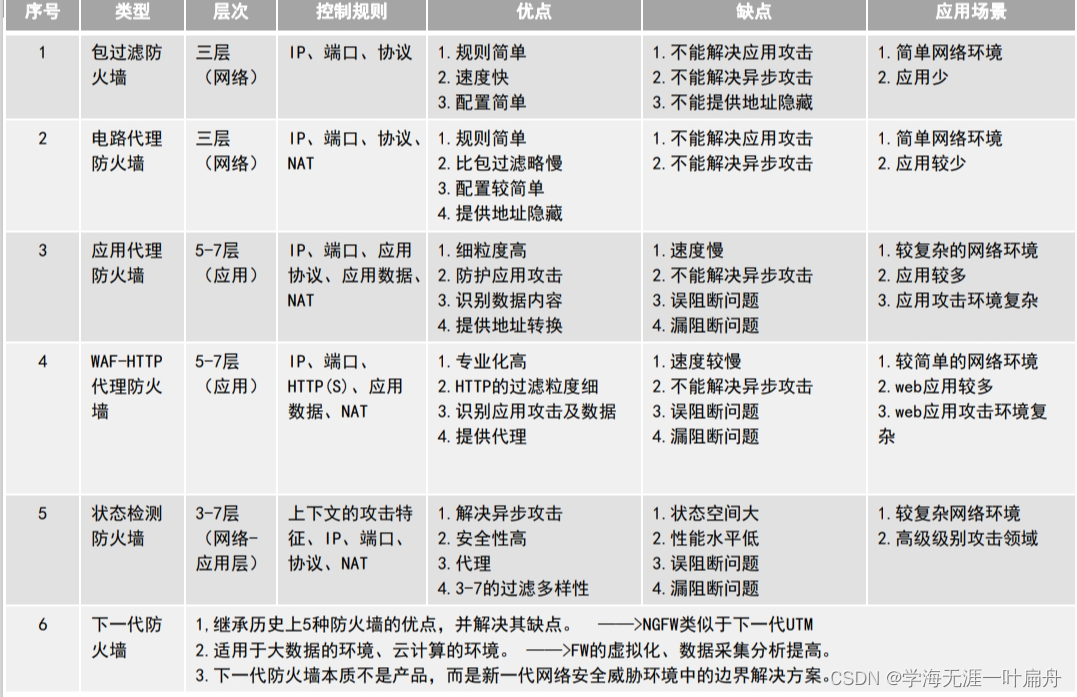
物流环境安全 场地选择考虑抗震、承重、防火、防水、供电、空气调节、电磁防护、雷击及静电 场地因素: 自然灾害,社会因素(加油站、化工厂),配套条件(消防,交通,电力,…...
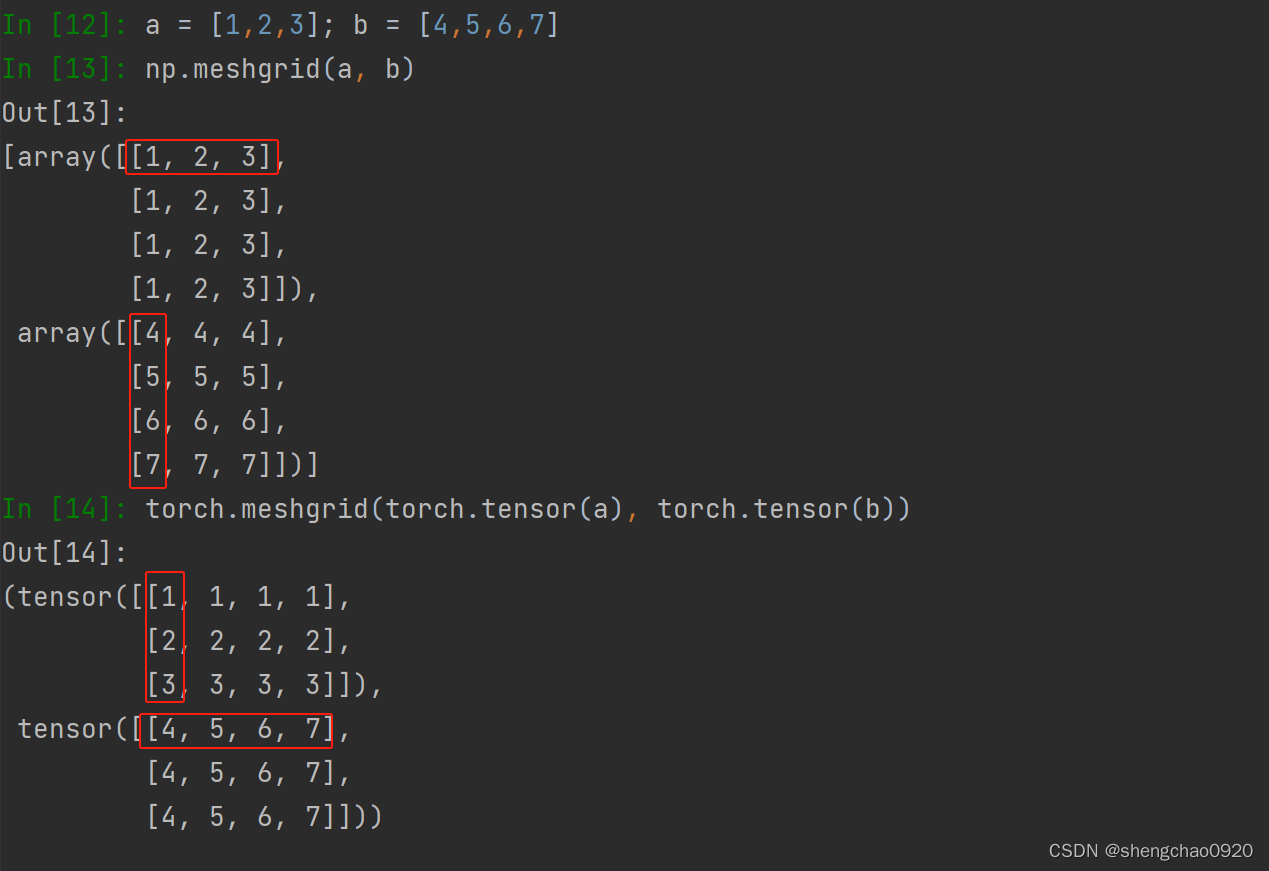
torch.meshgrid和np.meshgrid的区别
numpy中meshgrid: 把数组a当作一行,再根据数组b的长度扩充行。 把数组b当作一列,再根据数组a的长度扩充列。 torch中meshgrid: 把数组a当作一列,再根据数组b的长度扩充列。 把数组b当作一行,再根据数组a的…...

【PostgreSQL】约束-唯一约束
【PostgreSQL】约束链接 检查 唯一 主键 外键 排他 唯一约束 唯一约束是数据库中的一种约束,用于确保某个列或字段的值在该列或字段中是唯一的。唯一约束可用于确保数据库表中的某个列中的值是唯一的,也可用于确保多个列的组合值是唯一的。 在创建表…...

学习使用js/jquery获取指定class名称的三种方式
学习使用js/jquery获取指定class名称的三种方式 简介一、获取元素的class名称1、通过原生JS获取元素的class名称2、通过Jquery获取元素的class名称 二、应用1、样式修改2、动画效果实现 简介 在开发网页时,我们经常需要通过JS获取元素的class名称进行一些操作&…...

latex数学公式
写于:2024年1月5日 晚 修改: 摘要:数学公式根据其位置可以分为行内公式和行间公式。行内公式更加紧凑,而行间公式富于变化,可以为其编号、引用、换行等操作。本文对数学公式的 LaTex 做简单记录和整理。 行内公式 行内…...

frp配置内网穿透访问家里的nas
frp配置内网穿透访问家里的nas 需求 家里局域网内有台nas,在去公司的路上想访问它 其内网地址为: http://192.168.50.8:6002 工具 1.frp版本v0.53.2 下载地址: https://github.com/fatedier/frp/releases/download/v0.53.2/frp_0.53.2_li…...

C语言-蓝桥杯2023年第十四届省赛真题-砍树
题目描述 给定一棵由 n 个结点组成的树以及 m 个不重复的无序数对 (a1, b1), (a2, b2), . . . , (am, bm),其中 ai 互不相同,bi 互不相同,ai ≠ bj(1 ≤ i, j ≤ m)。 小明想知道是否能够选择一条树上的边砍断,使得对于每个 (a…...
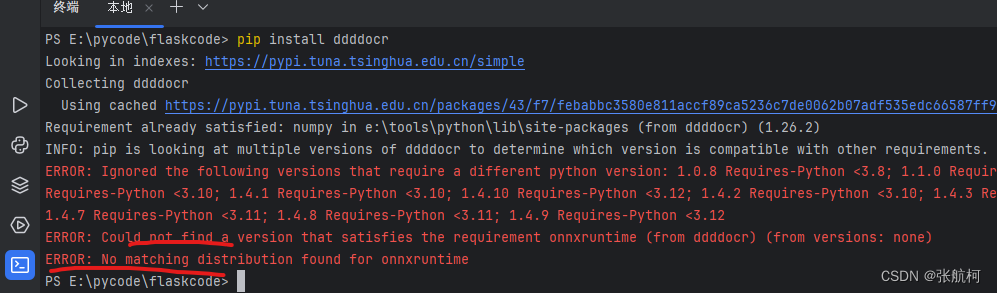
python识别验证码+灰度图片base64转换图片
一、为后面识别验证码准备 1、base64转换为图片,保存本地、并且置灰 上文中的base64,后面的就是包含Base64编码的PNG图像的字符串复制下来 import base64 from PIL import Image import io# 这里是你的Base64编码的字符串 base64_data "iVBORw0KGgoAAAANSUhE…...
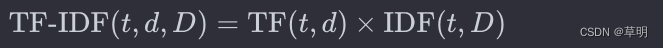
TF-IDF(Term Frequency-Inverse Document Frequency)算法 简介
TF-IDF(Term Frequency-Inverse Document Frequency)是一种用于信息检索和文本挖掘的常用算法。它用于评估一个词对于一个文档集合中某个文档的重要性。 这个算法的基本思想是:如果一个词在一个文档中频繁出现,并且在整个文档集合…...

企业怎么打造私域转化闭环?
一、私域矩阵构建 1、公众号 (1)流量来源:微信公众号既是私域流量的起点,亦为其源源不断的提供流量支持; (2)内容展示:公众号作为内容发布的主要渠道,可以通过公众号传…...

基于等保合规和滑动标尺模型的云安全建设方法
文章目录 前言一、云计算平台面临的安全挑战(一)新兴风险和传统风险的冲击(二) 云计算安全日益严峻,面临更大的安全挑战(三)提升对云计算平台的全面系统性安全建设的认知二、在云计算安全建设上的误区(一)缺乏整体视角构建云上安全,安全及运营存在割裂(二) 缺乏云内…...

MySQL数据库期末知识点总结(复习版)
一、数据库基本知识 数据库中的数据有什么特点 1、数据是按某种结构组织的 2、数据有整体性、共享性和较高的独立性 数据管理技术经历了哪三个阶段 1、手工管理 2、文件管理 3、数据库管理 数据库管理系统的主要功能有哪些 数据库管理系统的主要功能包括数据定义、数据…...
流行的Jmeter+Ant+Jenkins接口自动化测试框架在网络上走红
大致思路:Jmeter可以做接口测试,也能做压力测试,而且是开源软件;Ant是基于Java的构建工具,完成脚本执行并收集结果生成报告,可以跨平台,Jenkins是持续集成工具。将这三者结合起来可以搭建一套We…...

MySQL 数据页损坏处理思路
文章目录 前言1. 备份恢复2. 强制 InnoDB 恢复2.1 损坏数据页2.2 观察错误日志2.3 设置参数2.4 定位表信息2.5 分析处理2.6 恢复数据 总结 前言 研发自己搭建了一套 MySQL 没有设置双一参数,机房异常断电,导致数据页出现损坏,本篇文章介绍此…...

面试 Vue 框架八股文十问十答第二期
面试 Vue 框架八股文十问十答第二期 作者:程序员小白条,个人博客 相信看了本文后,对你的面试是有一定帮助的!关注专栏后就能收到持续更新! ⭐点赞⭐收藏⭐不迷路!⭐ 1)常见的事件修饰符及其作…...

【Python学习】2024PyCharm插件推荐
目录 【Python学习】2024PyCharm插件推荐 1. Key Promoter X2.Rainbow CSV3.Markdown4.Rainbow Brackets5.Indent Rainbow6.Regex Tester7.Regex Tester8.Background Image Plus9.Material Theme UI10. Chinese 汉化插件参考 文章所属专区 Python学习 1. Key Promoter X 方便…...

剑指offer题解合集——Week2day6
文章目录 剑指offerWeek2周六:表示数值的字符串AC代码思路: 周六:调整数组顺序使奇数位于偶数前面AC代码思路: 剑指offerWeek2 周六:表示数值的字符串 题目链接:表示数值的字符串 请实现一个函数用来判…...

算法训练第五十二天|300. 最长递增子序列、674. 最长连续递增序列、718. 最长重复子数组
300. 最长递增子序列: 题目链接 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组…...

HTTP基础知识总结
目录 一、什么是HTTP? 二、与HTTP有关的协议 三、HTTP请求特征 四、HTTP组成格式 五、HTTP标头 1.通用标头 2.实体标头 3.请求标头 4.响应标头 六、HTTP状态码分类 我们在日常测试过程中,也可以通过浏览器F12简单定位是前端问题还是后端问题&a…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...
